Regra 68–95–99,7 - 68–95–99.7 rule
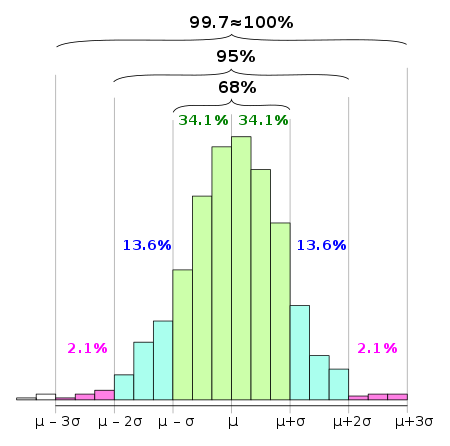

Nas estatísticas , a regra 68-95-99,7 , também conhecida como regra empírica , é uma abreviatura usada para lembrar a porcentagem de valores que estão dentro de uma estimativa de intervalo em uma distribuição normal : 68%, 95% e 99,7% do os valores estão dentro de um, dois e três desvios-padrão da média , respectivamente.
Em notação matemática, esses fatos podem ser expressos da seguinte forma, onde Χ é uma observação de uma variável aleatória normalmente distribuída , μ é a média da distribuição e σ é seu desvio padrão:
Nas ciências empíricas, a chamada regra empírica dos três sigma expressa uma heurística convencional de que quase todos os valores são considerados como estando dentro de três desvios-padrão da média e, portanto, é empiricamente útil tratar 99,7% de probabilidade como quase certeza. A utilidade dessa heurística depende especialmente da questão em consideração. Nas ciências sociais , um resultado pode ser considerado " significativo " se seu nível de confiança for da ordem de um efeito de dois sigma (95%), enquanto na física de partículas , há uma convenção de um efeito de cinco sigma (99,99994% confiança) sendo necessário para se qualificar como uma descoberta .
Uma regra de três sigma mais fraca pode ser derivada da desigualdade de Chebyshev , afirmando que mesmo para variáveis não normalmente distribuídas, pelo menos 88,8% dos casos devem cair dentro de intervalos de três sigma calculados corretamente. Para distribuições unimodais , a probabilidade de estar dentro do intervalo é de pelo menos 95% pela desigualdade Vysochanskij-Petunin . Pode haver certas suposições para uma distribuição que forçam essa probabilidade a ser de pelo menos 98%.
Função de distribuição cumulativa

Esses valores numéricos "68%, 95%, 99,7%" vêm da função de distribuição cumulativa da distribuição normal .
O intervalo de predição para qualquer pontuação padrão z corresponde numericamente a (1− (1− Φ μ , σ 2 (z)) · 2).
Por exemplo, Φ (2) ≈ 0,9772 , ou Pr ( X ≤ μ + 2 σ ) ≈ 0,9772 , correspondendo a um intervalo de predição de (1 - (1 - 0,97725) · 2) = 0,9545 = 95,45%. Este não é um intervalo simétrico - é apenas a probabilidade de que uma observação seja menor que μ + 2 σ . Para calcular a probabilidade de que uma observação esteja dentro de dois desvios padrão da média (pequenas diferenças devido ao arredondamento):
Isso está relacionado ao intervalo de confiança usado nas estatísticas: é aproximadamente um intervalo de confiança de 95% quando é a média de uma amostra de tamanho .
Testes de normalidade
A "regra 68-95-99,7" é frequentemente usada para obter rapidamente uma estimativa de probabilidade aproximada de algo, dado seu desvio padrão, se a população for considerada normal. Também é usado como um teste simples para outliers se a população for considerada normal e como um teste de normalidade se a população for potencialmente não normal.
Para passar de uma amostra a uma série de desvios-padrão, primeiro calcula-se o desvio , seja o erro ou residual, dependendo se se conhece a média da população ou apenas a estima. O próximo passo é padronizar (dividir pelo desvio padrão da população), se os parâmetros da população forem conhecidos, ou estudentizar (dividir por uma estimativa do desvio padrão), se os parâmetros forem desconhecidos e apenas estimados.
Para usar como um teste para outliers ou um teste de normalidade, calcula-se o tamanho dos desvios em termos de desvios padrão e compara-o à frequência esperada. Dado um conjunto de amostra, pode-se calcular os resíduos estudentizados e compará-los com a frequência esperada: os pontos que caem mais de 3 desvios-padrão da norma são provavelmente outliers (a menos que o tamanho da amostra seja significativamente grande, ponto em que se espera uma amostra extremo), e se houver muitos pontos a mais de 3 desvios-padrão da norma, é provável que haja motivos para questionar a normalidade assumida da distribuição. Isso é cada vez mais forte para movimentos de 4 ou mais desvios-padrão.
Pode-se calcular com mais precisão, aproximando o número de movimentos extremos de uma determinada magnitude ou maior por uma distribuição de Poisson , mas simplesmente, se houver vários movimentos de 4 desvios padrão em uma amostra de tamanho 1.000, terá um forte motivo para considerar esses valores discrepantes ou questionar a suposta normalidade da distribuição.
Por exemplo, um evento 6 σ corresponde a uma chance de cerca de duas partes por bilhão . Para ilustração, se os eventos ocorrerem diariamente, isso corresponderia a um evento esperado a cada 1,4 milhão de anos. Isso dá um teste de normalidade simples : se alguém testemunha um 6 σ nos dados diários e significativamente menos de 1 milhão de anos se passaram, então uma distribuição normal provavelmente não fornece um bom modelo para a magnitude ou frequência de grandes desvios a esse respeito.
Em The Black Swan , Nassim Nicholas Taleb dá o exemplo de modelos de risco segundo os quais o crash da Black Monday corresponderia a um evento 36- σ : a ocorrência de tal evento deveria instantaneamente sugerir que o modelo é falho, ou seja, que o processo sob consideração não é satisfatoriamente modelada por uma distribuição normal. Modelos refinados devem então ser considerados, por exemplo, pela introdução de volatilidade estocástica . Em tais discussões, é importante estar ciente do problema da falácia do jogador , que afirma que uma única observação de um evento raro não contradiz que o evento seja de fato raro. É a observação de uma pluralidade de eventos supostamente raros que cada vez mais abala a hipótese de que eles são raros, ou seja, a validade do modelo assumido. Uma modelagem adequada desse processo de perda gradual de confiança em uma hipótese envolveria a designação de probabilidade anterior não apenas para a própria hipótese, mas para todas as hipóteses alternativas possíveis. Por essa razão, o teste de hipótese estatística funciona não tanto ao confirmar uma hipótese considerada provável, mas ao refutar hipóteses consideradas improváveis .
Tabela de valores numéricos
Por causa das caudas exponenciais da distribuição normal, as chances de desvios maiores diminuem muito rapidamente. A partir das regras para dados normalmente distribuídos para um evento diário:
| Alcance | Fração esperada da população dentro do intervalo | Frequência aproximada esperada fora da faixa | Frequência aproximada para evento diário | |||
|---|---|---|---|---|---|---|
| μ ± 0,5σ | 0,382 924 922 548 026 | 3 dentro | 5 | Quatro ou cinco vezes por semana | ||
| μ ± σ | 0,682 689 492 137 086 | 1 in | 3 | Duas vezes por semana | ||
| μ ± 1,5σ | 0,866 385 597 462 284 | 1 in | 7 | Semanalmente | ||
| μ ± 2σ | 0,954 499 736 103 642 | 1 in | 22 | A cada três semanas | ||
| μ ± 2,5σ | 0,987 580 669 348 448 | 1 in | 81 | Trimestral | ||
| μ ± 3σ | 0,997 300 203 936 740 | 1 in | 370 | Anual | ||
| μ ± 3,5σ | 0,999 534 741 841 929 | 1 in | 2149 | A cada 6 anos | ||
| μ ± 4σ | 0,999 936 657 516 334 | 1 in | 15 787 | A cada 43 anos (duas vezes na vida) | ||
| μ ± 4,5σ | 0,999 993 204 653 751 | 1 in | 147 160 | A cada 403 anos (uma vez na era moderna) | ||
| μ ± 5σ | 0,999 999 426 696 856 | 1 in | 1 744 278 | Cada 4776 anos (uma vez na história registrada) | ||
| μ ± 5,5σ | 0,999 999 962 020 875 | 1 in | 26 330 254 | Cada 72 090 anos (três vezes na história da humanidade moderna ) | ||
| μ ± 6σ | 0,999 999 998 026 825 | 1 in | 506 797 346 | A cada 1,38 milhão de anos (duas vezes na história da humanidade ) | ||
| μ ± 6,5σ | 0,999 999 999 919 680 | 1 in | 12 450 197 393 | A cada 34 milhões de anos (duas vezes desde a extinção dos dinossauros ) | ||
| μ ± 7σ | 0,999 999 999 997 440 | 1 in | 390 682 215 445 | A cada 1,07 bilhão de anos (quatro ocorrências na história da Terra ) | ||
| μ ± x σ | 1 in | Todos os dias | ||||
Veja também
Referências
links externos
- " The Normal Distribution " por Balasubramanian Narasimhan
- " Calcular a proporção percentual dentro de x sigmas em WolframAlpha







