Modificação de amplitude - Amplitude-shift keying
| Modulação de banda passante |
|---|
| Modulação analógica |
| Modulação digital |
| Modulação hierárquica |
| Espalhe o espectro |
| Veja também |
Amplitude-shift keying ( ASK ) é uma forma de modulação de amplitude que representa dados digitais como variações na amplitude de uma onda portadora . Em um sistema ASK, um símbolo , representando um ou mais bits , é enviado pela transmissão de uma onda portadora de amplitude fixa em uma frequência fixa por um período de tempo específico. Por exemplo, se cada símbolo representa um único bit, o sinal da portadora será transmitido quando o valor de entrada for 1, mas não será transmitido quando o valor de entrada for 0.
Qualquer esquema de modulação digital usa um número finito de sinais distintos para representar os dados digitais. ASK usa um número finito de amplitudes, cada uma atribuída a um padrão único de dígitos binários . Normalmente, cada amplitude codifica um número igual de bits. Cada padrão de bits forma o símbolo que é representado pela amplitude particular. O demodulador , que é projetado especificamente para o conjunto de símbolos usado pelo modulador, determina a amplitude do sinal recebido e mapeia de volta para o símbolo que representa, recuperando assim os dados originais. A frequência e a fase da portadora são mantidas constantes.
Como o AM , um ASK também é linear e sensível ao ruído atmosférico, distorções, condições de propagação em diferentes rotas no PSTN , etc. Ambos os processos de modulação e demodulação ASK são relativamente baratos. A técnica ASK também é comumente usada para transmitir dados digitais por fibra óptica. Para transmissores de LED, o binário 1 é representado por um pulso curto de luz e o binário 0 pela ausência de luz. Os transmissores de laser normalmente têm uma corrente de "polarização" fixa que faz com que o dispositivo emita um nível de luz baixo. Este nível baixo representa o binário 0, enquanto uma onda de luz de maior amplitude representa o binário 1.
A forma mais simples e comum de ASK opera como uma chave, usando a presença de uma onda portadora para indicar um binário e sua ausência para indicar um zero binário. Este tipo de modulação é chamado de on-off keying (OOK) e é usado em radiofrequências para transmitir código Morse (conhecido como operação de onda contínua),
Esquemas de codificação mais sofisticados foram desenvolvidos, os quais representam dados em grupos usando níveis de amplitude adicionais. Por exemplo, um esquema de codificação de quatro níveis pode representar dois bits com cada mudança de amplitude; um esquema de oito níveis pode representar três bits; e assim por diante. Essas formas de chaveamento de amplitude requerem uma alta relação sinal-ruído para sua recuperação, já que, por sua natureza, grande parte do sinal é transmitido com potência reduzida.
O sistema ASK pode ser dividido em três blocos. O primeiro representa o transmissor, o segundo é um modelo linear dos efeitos do canal, o terceiro mostra a estrutura do receptor. A seguinte notação é usada:
- h t (f) é o sinal da portadora para a transmissão
- h c (f) é a resposta ao impulso do canal
- n (t) é o ruído introduzido pelo canal
- h r (f) é o filtro no receptor
- L é o número de níveis que são usados para transmissão
- T s é o tempo entre a geração de dois símbolos
Símbolos diferentes são representados com tensões diferentes. Se o valor máximo permitido para a tensão for A, todos os valores possíveis estão na faixa [−A, A] e são dados por:
a diferença entre uma tensão e a outra é:
Considerando a figura, os símbolos v [n] são gerados aleatoriamente pela fonte S, então o gerador de impulsos cria impulsos com área de v [n]. Esses impulsos são enviados ao filtro ht para serem enviados através do canal. Em outras palavras, para cada símbolo, uma onda portadora diferente é enviada com a amplitude relativa.
Fora do transmissor, o sinal s (t) pode ser expresso na forma:
No receptor, após a filtragem por hr (t), o sinal é:
onde usamos a notação:
onde * indica a convolução entre dois sinais. Após a conversão A / D, o sinal z [k] pode ser expresso na forma:
Nesta relação, o segundo termo representa o símbolo a ser extraído. Os outros são indesejados: o primeiro é o efeito do ruído, o terceiro é devido à interferência intersimbólica.
Se os filtros forem escolhidos de forma que g (t) satisfaça o critério ISI de Nyquist, então não haverá interferência intersimbólica e o valor da soma será zero, então:
a transmissão será afetada apenas pelo ruído.
Probabilidade de erro
A função de densidade de probabilidade de ter um erro de um determinado tamanho pode ser modelada por uma função Gaussiana; o valor médio será o valor relativo enviado, e sua variação será dada por:
onde é a densidade espectral do ruído dentro da banda e Hr (f) é a transformada de Fourier contínua da resposta ao impulso do filtro hr (f).
A probabilidade de cometer um erro é dada por:
onde, por exemplo, é a probabilidade condicional de cometer um erro dado que um símbolo v0 foi enviado e é a probabilidade de enviar um símbolo v0.
Se a probabilidade de enviar qualquer símbolo for a mesma, então:
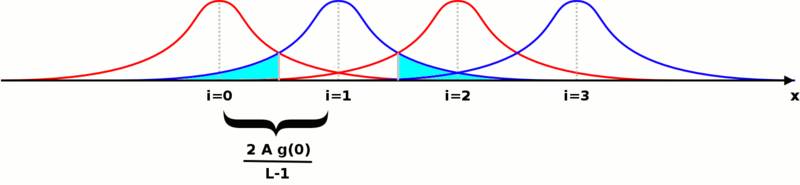
Se representarmos todas as funções de densidade de probabilidade no mesmo gráfico contra o valor possível da voltagem a ser transmitida, obteremos uma imagem como esta (o caso particular de é mostrado):
A probabilidade de cometer um erro após o envio de um único símbolo é a área da função gaussiana que se enquadra nas funções dos outros símbolos. É mostrado em ciano apenas para um deles. Se chamarmos a área sob um lado do Gaussian, a soma de todas as áreas serão: . A probabilidade total de cometer um erro pode ser expressa na forma:
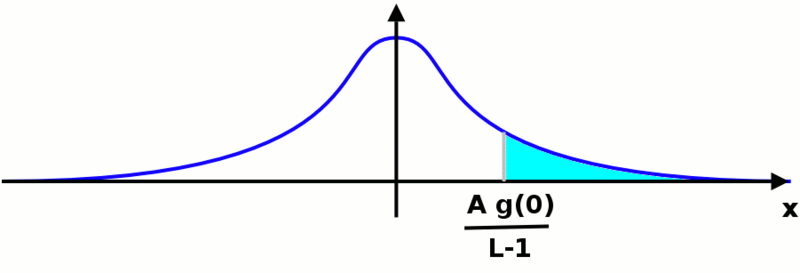
Agora temos que calcular o valor de . Para fazer isso, podemos mover a origem da referência para onde quisermos: a área abaixo da função não mudará. Estamos em uma situação como a mostrada na figura a seguir:
não importa qual função gaussiana estamos considerando, a área que queremos calcular será a mesma. O valor que procuramos será dado pela seguinte integral:
onde está a função de erro complementar. Juntando todos esses resultados, a probabilidade de cometer um erro é:
a partir desta fórmula podemos compreender facilmente que a probabilidade de cometer um erro diminui se a amplitude máxima do sinal transmitido ou a amplificação do sistema se torna maior; por outro lado, aumenta se o número de níveis ou a potência do ruído se tornarem maiores.
Esta relação é válida quando não há interferência intersimbólica, ou seja, é uma função de Nyquist .
Veja também
- Mudança de frequência (FSK)




![s (t) = \ sum_ {n = - \ infty} ^ \ infty v [n] \ cdot h_t (t - n T_s)](https://wikimedia.org/api/rest_v1/media/math/render/svg/90a0b550c811dd0d2b451068cf1c4ba4fb34895b)
![{\ displaystyle z (t) = n_ {r} (t) + \ sum _ {n = - \ infty} ^ {\ infty} v [n] \ cdot g (t-nT_ {s})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a96e3e86c428e56323da21a9825580fb170f5a77)

![z [k] = n_r [k] + v [k] g [0] + \ sum_ {n \ neq k} v [n] g [kn]](https://wikimedia.org/api/rest_v1/media/math/render/svg/357e87edded3e22b8152039a30afb145410130f2)
![z [k] = n_r [k] + v [k] g [0]](https://wikimedia.org/api/rest_v1/media/math/render/svg/5a159a61e7a4ec3d3f1d1041b9e94496cc15f221)