Ângulo de paralelismo - Angle of parallelism

Se o ângulo B está à direita e Aa e Bb são limitativos paralelo , em seguida, o ângulo entre Aa e AB é o ângulo de paralelismo.

Na geometria hiperbólica , o ângulo de paralelismo , é o ângulo no vértice de um certo um triângulo hiperbólica que tem duas paralelas assimptóticas lados. O ângulo depende do comprimento do segmento de um entre o ângulo direito e o vértice do ângulo de paralelismo. ${\ Displaystyle \ Pi (a)}$

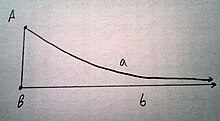
Dado um ponto fora de uma linha, se soltar uma perpendicular à linha a partir do ponto, em seguida, uma é a distância ao longo deste segmento perpendicular, e φ ou é o mínimo ângulo de tal modo que a linha traçada através do ponto em que o ângulo não faz intersectar a linha dado. Desde dois lados são assintótica paralelo, ${\ Displaystyle \ Pi (a)}$

${\ Displaystyle \ lim _ {a \ to 0} \ Pi (a) = {\ tfrac {1} {2}} \ pi \ quad {\ text {e}} \ quad \ lim _ {a \ a \ infty } \ Pi (a) = 0.}$

Há cinco expressões equivalentes que se relacionam e um : ${\ Displaystyle \ Pi (a)}$

${\ Displaystyle \ sin \ Pi (a) = \ operatorname {sech} a = {\ frac {1} {\ cosh um}} = {\ frac {2} {e ^ {a} + e ^ {- a} }} \,}$

${\ Displaystyle \ cos \ Pi (a) = \ a = tanh {\ frac {e ^ {a} -e ^ {-} {a} e ^ {a} + e ^ {- a}}} \,}$

${\ Displaystyle \ tan \ Pi (a) = \ operatorname {csch} a = {\ frac {1} {\ sinh um}} = {\ frac {2} {e ^ {a} -e ^ {- a} }} \,}$

${\ Displaystyle \ tan \ esquerda ({\ tfrac {1} {2}} \ Pi (a) \ direita) = e ^ {- a},}$

${\ Displaystyle \ Pi (a) = {\ tfrac {1} {2}} \ pi - \ operatorname {gd} (a),}$

onde sinh, cosh, tanh, sech e csch são funções hiperbólicas e gd é a função gudermanniana .

Construção

János Bolyai descobriu uma construção que dá os paralelas assimptóticas s para uma linha de r que passa através de um ponto A não em r . Deixar cair uma perpendicular a partir de uma para B no r . Escolher qualquer ponto C no r diferente de B . Erigir uma perpendicular t a r a C . Deixar cair uma perpendicular a partir de uma para D em t . Então comprimento DA é mais do que CB , mas mais curto do CA . Desenhar um círculo em torno C com raio igual a DA . Ele vai intersectar o segmento AB num ponto E . Em seguida, o ângulo BEC é independente do comprimento BC , dependendo apenas de AB ; é o ângulo de paralelismo. Construir s através de uma em ângulo BEC a partir de AB .

${\ Displaystyle \ pecado BEC = {\ frac {\ sinh {BC}} {\ sinh {CE}}} = {\ frac {\ sinh {BC}} {\ sinh {DA}}} = {\ frac {\ sinh {BC}} {\ sin {ACD} \ sinh {CA}}} = {\ frac {\ sinh {BC}} {\ cos {ACB} \ sinh {CA}}} = {\ frac {\ sinh { BC} \ tanh {CA}} {\ tanh {CB} \ sinh {CA}}} = {\ frac {\ cosh {BC}} {\ cosh {CA}}} = {\ frac {\ cosh {BC} } {\ cosh {CB} \ cosh {AB}}} = {\ frac {1} {\ cosh {AB}}} \ ,.}$

Veja trigonometria de triângulos retângulos para as fórmulas utilizadas aqui.

História

O ângulo de paralelismo foi desenvolvido em 1840 na publicação alemã "zur Teoria Geometrische Untersuchungen der Parallellinien" por Nicolai Lobachevsky .

Esta publicação se tornou amplamente conhecido em Inglês depois que o professor Texas GB Halsted apresentada uma tradução em 1891. ( geométricas Pesquisas sobre a teoria da Parallels )

Os seguintes passagens definir este conceito fundamental na geometria hiperbólica:

O ângulo entre a HAD HA paralelo e perpendicular a AD é chamado o ângulo paralelo (ângulo de paralelismo) que vamos designar aqui por Π (p) para o AD = p .

demonstração

O ângulo de paralelismo, φ , formulados na forma de: (a) o ângulo entre o eixo x e a linha traçada a partir de x , o centro de Q , para y , a intercepção de y de Q, e (b) O ângulo a partir da tangente de Q em y com o eixo y.
Este diagrama, com amarelo triângulo ideal , é semelhante ao encontrado em um livro por Smogorzhevsky.

No modelo semi-plano Poincaré do plano hiperbólico (ver movimentos hiperbólicas ), pode-se estabelecer a relação de φ para um com a geometria euclidiana . Deixe Q ser o semicírculo com diâmetro no x -axis que passa através dos pontos (1,0) e (0, y ), onde y > 1. Uma vez que Q é tangente à unidade de semicírculo centrada na origem, os dois semicírculos representam linhas paralelas hiperbólicas . O y -axis atravessa ambos os semicírculos, fazendo um ângulo recto com a unidade de semicírculo e um ângulo variável φ com Q . O ângulo ao centro de Q subtendido pelo raio para (0,  y ) é também φ porque os dois ângulos de ter lados que são perpendiculares, o lado esquerdo para o lado esquerdo, e no lado direito para o lado direito. O semicírculo Q tem o seu centro em ( x , 0), x <0, então o seu raio é 1 -  x . Assim, o raio ao quadrado de Q é

${\ Displaystyle x ^ {2} + y ^ {2} = (1-x) ^ {2},}$

conseqüentemente

${\ Displaystyle x = {\ tfrac {1} {2}} (1-y ^ {2}).}$

A métrica do modelo semi-plano Poincaré da geometria hiperbólica parametriza distância no raio {(0,  y ): y > 0} com medida logarítmica . Deixe log  y = um modo, y = e ^um em que E é a base do logaritmo natural . Então, a relação entre φ e um pode ser deduzida a partir do triângulo {( x , 0), (0, 0), (0,  y )}, por exemplo:

${\ Displaystyle \ tan \ phi = {\ frac {y} {- x}} = {\ frac {2y} {y ^ {2} -1}} = {\ frac {2e ^ {a}} {e ^ {2a} -1}} = {\ frac {1} {\ sinh um}}.}$

Referências

• Marvin J. Greenberg (1974) euclidiana e não-euclideana Geometrias , pp 211-3., WH Freeman & Company .
• Robin Hartshorne (1997) Companion a Euclides pp. 319, 325, American Mathematical Society , ISBN  0821807978 .
• Jeremy Gray (1989) idéias de espaço: Euclidiana, não-euclidiana, e relativista , 2ª edição, Clarendon Press , Oxford (Veja as páginas 113 a 118).
• Béla Kerékjártó (1966) Les Fondements de la geometria , Tomo deux, §97.6 Ângulo de parallélisme de la geometria hyperbolique, pp. 411,2, Akadémiai Kiado, Budapeste.