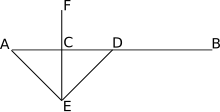
Bissecção - Bisection
Em geometria , bissecção é a divisão de algo em duas partes iguais ou congruentes , geralmente por uma linha , que é então chamada de bissetriz . Os tipos de bissetriz mais frequentemente considerados são a bissetriz do segmento (uma linha que passa pelo ponto médio de um determinado segmento ) e a bissetriz do ângulo (uma linha que passa pelo vértice de um ângulo , que o divide em dois ângulos iguais).
No espaço tridimensional , a bissecção geralmente é feita por um plano, também chamado de bissetriz ou plano de bissetriz .
Bissetriz do segmento de linha perpendicular
Definição
- A bissetriz perpendicular de um segmento de linha é uma linha que encontra o segmento em seu ponto médio perpendicularmente.
A bissetriz perpendicular de um segmento também tem a propriedade de que cada um de seus pontos seja equidistante dos pontos finais do segmento: (D) .
A prova decorre e teorema de Pitágoras :
A propriedade (D) é geralmente usada para a construção de uma bissetriz perpendicular:
Construção por régua e compasso
Na geometria clássica, a bissecção é uma construção simples de compasso e régua , cuja possibilidade depende da capacidade de desenhar círculos de raios iguais e centros diferentes:
O segmento é dividido ao meio desenhando círculos de interseção de raios iguais , cujos centros são os pontos finais do segmento. A linha determinada pelos pontos de intersecção dos dois círculos é a bissetriz perpendicular do segmento.
Como a construção da bissetriz é feita sem o conhecimento do ponto médio do segmento , a construção é usada para determinar como a intersecção da bissetriz e o segmento de linha.
Esta construção é de fato usada quando se constrói uma reta perpendicular a uma dada reta em um dado ponto : traçando um círculo cujo centro é tal que cruza a reta em dois pontos , e a perpendicular a ser construída é o segmento de bissetriz .
Equações
Se forem os vetores de posição de dois pontos , então seu ponto médio é e o vetor é um vetor normal da bissetriz do segmento de reta perpendicular. Portanto, sua equação vetorial é . Inserir e expandir a equação leva à equação vetorial
(V)
Com um obtém-se a equação na forma de coordenadas:
(C)
Ou explicitamente:
(E) ,
onde , e .
Formulários
Bissetores de segmento de linha perpendicular foram usados resolvendo vários problemas geométricos:
- Construção do centro de um círculo de Thales ,
- Construção do centro do Círculo de um triângulo,
- Os limites do diagrama de Voronoi consistem em segmentos de tais linhas ou planos.
Bissetores de segmento de linha perpendicular no espaço
- A bissetriz perpendicular de um segmento de linha é um plano que encontra o segmento em seu ponto médio perpendicularmente.
Sua equação vetorial é literalmente a mesma que no caso do plano:
(V)
Com um obtém-se a equação na forma de coordenadas:
(C3)
Propriedade (D) (ver acima) é literalmente verdadeiro no espaço, também:
(D) O plano bissector perpendicular de um segmento tem para qualquer ponto do alojamento: .
Bissetriz angular
Uma bissetriz de ângulo divide o ângulo em dois ângulos com medidas iguais . Um ângulo tem apenas uma bissetriz. Cada ponto de uma bissetriz do ângulo é equidistante dos lados do ângulo.
O interior ou bissectriz interna de um ângulo é a linha, meia-linha , ou segmento de linha que divide um ângulo inferior a 180 ° em dois ângulos iguais. O exterior ou bissectriz externa é a linha que divide o ângulo suplementar (de 180 ° menos o ângulo original), formada por um lado que forma o ângulo original e a extensão do outro lado, em dois ângulos iguais.
Para dividir um ângulo com régua e compasso , desenha-se um círculo cujo centro é o vértice. O círculo encontra o ângulo em dois pontos: um em cada perna. Usando cada um desses pontos como centro, desenhe dois círculos do mesmo tamanho. A intersecção dos círculos (dois pontos) determina uma linha que é a bissetriz do ângulo.
A prova da correção dessa construção é bastante intuitiva, contando com a simetria do problema. A trissecção de um ângulo (dividindo-o em três partes iguais) não pode ser alcançada apenas com o compasso e a régua (isso foi provado pela primeira vez por Pierre Wantzel ).
As bissetoras interna e externa de um ângulo são perpendiculares . Se o ângulo é formado pelas duas retas dadas algebricamente como e então as bissetoras interna e externa são dadas pelas duas equações
Triângulo
Concorrências e colinearidades
As bissetoras dos ângulos internos de um triângulo são simultâneas em um ponto denominado incentivo do triângulo, conforme mostrado no diagrama à direita.
As bissetoras de dois ângulos externos e a bissetriz do outro ângulo interno são concorrentes.
Três pontos de intersecção, cada um de uma bissetriz do ângulo externo com o lado estendido oposto , são colineares (caem na mesma linha que os outros).
Três pontos de intersecção, dois deles entre uma bissetriz do ângulo interno e o lado oposto, e o terceiro entre a outra bissetriz do ângulo externo e o lado oposto estendido, são colineares.
Teorema da bissetriz do ângulo
O teorema da bissetriz do ângulo se preocupa com os comprimentos relativos dos dois segmentos em que o lado do triângulo é dividido por uma linha que divide o ângulo oposto. Ele iguala seus comprimentos relativos aos comprimentos relativos dos outros dois lados do triângulo.
Comprimentos
Se os comprimentos dos lados de um triângulo forem , o semiperímetro e A são o lado oposto do ângulo , então o comprimento da bissetriz interna do ângulo A é
ou em termos trigonométricos,
Se a bissetriz interna do ângulo A no triângulo ABC tiver comprimento e se essa bissetriz dividir o lado oposto A em segmentos de comprimentos m e n , então
onde b e c são os comprimentos laterais opostos aos vértices B e C; e o lado oposto a A é dividido na proporção b : c .
Se as bissetoras internas dos ângulos A, B e C têm comprimentos e , então
Não há dois triângulos não congruentes que compartilhem o mesmo conjunto de três comprimentos de bissetriz de ângulo interno.
Triângulos inteiros
Existem triângulos inteiros com uma bissetriz de ângulo racional .
Quadrilátero
As bissetoras do ângulo interno de um quadrilátero convexo formam um quadrilátero cíclico (isto é, os quatro pontos de interseção das bissetoras dos ângulos adjacentes são concíclicos ) ou são concorrentes . No último caso, o quadrilátero é um quadrilátero tangencial .
Losango
Cada diagonal de um losango divide ângulos opostos.
Quadrilátero Ex-tangencial
O excentro de um quadrilátero ex-tangencial encontra-se na intersecção de seis bissetores de ângulo. Estas são as bissetoras do ângulo interno em dois ângulos de vértice opostos, as bissetoras do ângulo externo (bissetriz do ângulo suplementar) nos outros dois ângulos do vértice e as bissetoras do ângulo externo nos ângulos formados onde as extensões dos lados opostos se cruzam.
Parábola
A tangente a uma parábola em qualquer ponto divide o ângulo entre a linha que une o ponto ao foco e a linha do ponto e perpendicular à diretriz.
Bissetores dos lados de um polígono
Triângulo
Medianas
Cada uma das três medianas de um triângulo é um segmento de linha que atravessa um vértice e o ponto médio do lado oposto, então divide esse lado (embora não perpendicularmente). As três medianas se cruzam em um ponto denominado centróide do triângulo, que é seu centro de massa se tiver densidade uniforme; assim, qualquer linha através do centróide de um triângulo e um de seus vértices corta o lado oposto ao meio. O centróide está duas vezes mais próximo do ponto médio de qualquer lado do que do vértice oposto.
Bissetores perpendiculares
A bissetriz perpendicular interior de um lado de um triângulo é o segmento, caindo inteiramente sobre e dentro do triângulo, da linha que divide perpendicularmente esse lado. As três bissetoras perpendiculares dos três lados de um triângulo se cruzam no circuncentro (o centro do círculo através dos três vértices). Assim, qualquer linha que atravesse o circuncentro de um triângulo e seja perpendicular a um lado corta esse lado.
Em um triângulo agudo, o circuncentro divide os bissetores perpendiculares internos dos dois lados mais curtos em proporções iguais. Em um triângulo obtuso, os dois lados mais curtos bissetores perpendiculares (estendidos além de seus lados opostos do triângulo até o circuncentro) são divididos por seus respectivos lados do triângulo que se cruzam em proporções iguais.
Para qualquer triângulo, os bissetores perpendiculares internos são dados por e onde os lados estão e a área é
Quadrilátero
Os dois bimedianos de um quadrilátero convexo são os segmentos de linha que conectam os pontos médios de lados opostos, portanto, cada um divide dois lados. Os dois bimedianos e o segmento de linha que une os pontos médios das diagonais são concorrentes em um ponto denominado "centróide do vértice" e são todos divididos ao meio por este ponto.
As quatro "maltitudes" de um quadrilátero convexo são as perpendiculares a um lado através do ponto médio do lado oposto, dividindo assim o último lado. Se o quadrilátero é cíclico (inscrito em um círculo), essas maltitudes são simultâneas em (todas se encontram) em um ponto comum denominado "anticentro".
O teorema de Brahmagupta afirma que se um quadrilátero cíclico é ortogonal (ou seja, tem diagonais perpendiculares ), então a perpendicular a um lado do ponto de intersecção das diagonais sempre corta o lado oposto ao meio.
A construção bissetriz perpendicular forma um quadrilátero a partir das bissetoras perpendiculares dos lados de outro quadrilátero.
Bissetriz de área e bissetriz de perímetro
Triângulo
Há uma infinidade de linhas que dividem a área de um triângulo . Três deles são as medianas do triângulo (que conectam os pontos médios dos lados com os vértices opostos), e estes são concorrentes no centróide do triângulo ; na verdade, eles são as únicas bissetoras de área que passam pelo centróide. Três outras bissetoras de área são paralelas aos lados do triângulo; cada um deles cruza os outros dois lados de modo a dividi-los em segmentos com as proporções . Essas seis linhas são simultâneas, três de cada vez: além de as três medianas serem simultâneas, qualquer mediana é concorrente com duas das bissetoras da área paralela lateral.
O envelope da infinidade de bissetores de área é um deltóide (amplamente definido como uma figura com três vértices conectados por curvas côncavas ao exterior do deltóide, tornando os pontos internos um conjunto não convexo). Os vértices do deltóide estão nos pontos médios das medianas; todos os pontos dentro do deltóide estão em três bissetores de área diferentes, enquanto todos os pontos fora dele estão em apenas uma. [1] Os lados do deltóide são arcos de hipérboles que são assimptótica para os lados prolongados do triângulo. A proporção da área do envelope das bissetoras da área para a área do triângulo é invariante para todos os triângulos e é igual a, por exemplo, 0,019860 ... ou menos de 2%.
Um cutelo de um triângulo é um segmento de linha que corta o perímetro do triângulo e tem um ponto final no ponto médio de um dos três lados. Os três cutelos coincidem (todos passam) no centro do círculo de Spieker , que é o círculo interno do triângulo medial . Os cutelos são paralelos às bissetoras do ângulo.
Um divisor de um triângulo é um segmento de linha que tem um ponto final em um dos três vértices do triângulo e divide o perímetro ao meio. Os três divisores coincidem no ponto Nagel do triângulo.
Qualquer linha através de um triângulo que divide a área do triângulo e seu perímetro ao meio passa pelo incentivo do triângulo (o centro de seu círculo interno ). Existem um, dois ou três deles para qualquer triângulo. Uma linha através do incentivo corta ao meio uma da área ou perímetro se, e somente se, corta também ao meio o outro.
Paralelogramo
Qualquer linha através do ponto médio de um paralelogramo corta a área e o perímetro ao meio.
Círculo e elipse
Todas as bissetoras de área e bissetoras de perímetro de um círculo ou outra elipse passam pelo centro , e quaisquer cordas pelo centro dividem a área e o perímetro. No caso de um círculo, eles são os diâmetros do círculo.
Bissetores de diagonais
Paralelogramo
As diagonais de um paralelogramo se dividem entre si.
Quadrilátero
Se um segmento de linha conectando as diagonais de um quadrilátero corta ao meio ambas as diagonais, então este segmento de linha (a Linha de Newton ) é ele próprio dividido ao meio pelo centróide do vértice.
Bissetoras de volume
Um plano que divide duas arestas opostas de um tetraedro em uma determinada proporção também divide o volume do tetraedro na mesma proporção. Assim, qualquer plano contendo um bimediano (conector de pontos médios de bordas opostas) de um tetraedro corta o volume do tetraedro ao meio
Referências
- ^ Weisstein, Eric W. "Exterior Angle Bisector." From MathWorld - A Wolfram Web Resource.
- ^ Espanha, Barry. Analytical Conics , Dover Publications, 2007 (orig. 1957).
- ^ a b c d e Johnson, Roger A., geometria euclidiana avançada , Dover Publ., 2007 (orig. 1929).
- ^ Oxman, Victor. "Sobre a existência de triângulos com determinados comprimentos de um lado e dois bissetores de ângulo adjacentes", Forum Geometricorum 4, 2004, 215–218. http://forumgeom.fau.edu/FG2004volume4/FG200425.pdf
- ^ Simons, Stuart. Mathematical Gazette 93, March 2009, 115-116.
- ^ Mironescu, P., e Panaitopol, L., "A existência de um triângulo com comprimentos bissetores de ângulo prescritos", American Mathematical Monthly 101 (1994): 58-60.
- ^ Oxman, Victor, "Uma prova puramente geométrica da singularidade de um triângulo com bissetores de ângulo prescritos", Forum Geometricorum 8 (2008): 197–200.
- ^ Weisstein, Eric W. "Quadrilateral." From MathWorld - A Wolfram Web Resource. http://mathworld.wolfram.com/Quadrilateral.html
- ^ a b Mitchell, Douglas W. (2013), "Perpendicular Bisectors of Triangle Sides", Forum Geometricorum 13, 53-59. http://forumgeom.fau.edu/FG2013volume13/FG201307.pdf
- ^ Altshiller-Corte, Nathan, geometria da faculdade , Dover Publ., 2007.
- ^ a b c Dunn, JA, and Pretty, JE, "Halving a triangle," Mathematical Gazette 56, maio de 1972, 105-108.
- ^ Kodokostas, Dimitrios, "Triangle Equalizers", Mathematics Magazine 83, abril de 2010, pp. 141-146.
- ^ Dunn, JA e JE Pretty, "Halving a triangle", Mathematical Gazette 56, maio de 1972, p. 105
- ^ Weisstein, Eric W. "Tetrahedron". From MathWorld - A Wolfram Web Resource. http://mathworld.wolfram.com/Tetrahedron.html
- ^ Altshiller-Court, N. "O tetraedro." CH. 4 em Modern Pure Solid Geometry : Chelsea, 1979.
links externos
- O Bisector do Ângulo em corte-o-nó
- Definição do bisector do ângulo. Referência de matemática aberta com miniaplicativo interativo
- Definição da linha divisória. Referência de matemática aberta com miniaplicativo interativo
- Bissetriz da linha perpendicular. Com miniaplicativo interativo
- Instruções animadas para dividir um ângulo e dividir uma linha usando uma bússola e régua
- Weisstein, Eric W. "Line Bisector" . MathWorld .
Este artigo incorpora material da bissetriz de Angle no PlanetMath , que é licenciado sob a licença Creative Commons Atribuição / Compartilhamento pela mesma Licença .