Jogo Blotto - Blotto game
Um jogo Coronel Blotto é um tipo de jogo de soma constante de duas pessoas em que os jogadores (oficiais) são encarregados de distribuir simultaneamente recursos limitados por vários objetos (campos de batalha).
Na versão clássica do jogo, o jogador que dedica mais recursos a um campo de batalha vence aquele campo de batalha, e o ganho (ou recompensa) é igual ao número total de campos de batalha ganhos.
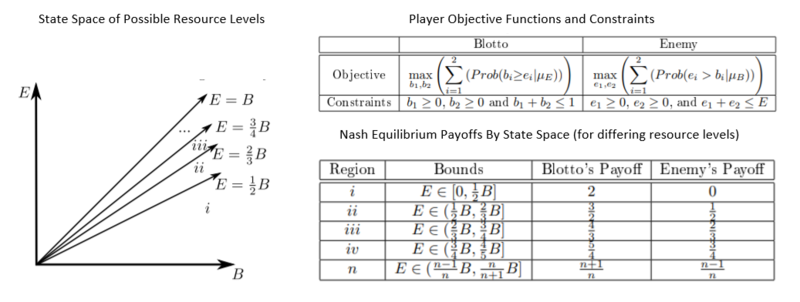
Considere dois jogadores (Coronel Blotto e Inimigo), dois campos de batalha, ambos de igual valor, ambos os jogadores conhecem o nível total de recursos um do outro antes da alocação e, então, devem tomar uma decisão simultânea de alocação. Freqüentemente, presume-se que o Coronel Blotto é o oficial com mais recursos (seu nível de recursos pode ser definido como 1) e o Inimigo tem uma fração de recursos menor que 1. As estratégias de alocação de equilíbrio de Nash e recompensas dependem dessa relação de nível de recurso.
O jogo Coronel Blotto foi proposto pela primeira vez por Émile Borel em 1921. O jogo foi estudado após a Segunda Guerra Mundial por estudiosos da Pesquisa Operacional e se tornou um clássico na teoria dos jogos . O artigo de Gross e Wagner de 1950, do qual o fictício Coronel Blotto and Enemy obteve seu nome, fornece alguns exemplos de equilíbrio de Nash. Macdonell e Mastronardi 2015 fornecem a primeira caracterização completa de todos os equilíbrios de Nash para a versão canônica mais simples do jogo Coronel Blotto. Esta solução, que inclui um algoritmo gráfico para caracterizar todas as estratégias de equilíbrio de Nash, inclui estratégias de equilíbrio de Nash não previamente identificadas e também ajuda a identificar quais comportamentos nunca devem ser esperados por jogadores racionais. As estratégias de equilíbrio de Nash nesta versão do jogo são um conjunto de distribuições de probabilidade bivariadas: distribuições sobre um conjunto de alocações de recursos possíveis para cada jogador, muitas vezes referido como Equilíbrio de Nash misto (como pode ser encontrado em Paper-Rock-Scissors ou Matching Centavos como exemplos muito mais simples).
A solução, prova e algoritmo gráfico de Macdonell e Mastronardi 2015 para identificar estratégias de equilíbrio de Nash também pertencem a versões generalizadas do jogo, como quando o Coronel Blotto tem avaliações diferentes dos campos de batalha, quando seus recursos têm eficácia diferente nos dois campos de batalha (por exemplo, um campo de batalha inclui um pouso na água e os recursos do Coronel Blotto são fuzileiros navais em vez de soldados), e fornece insights sobre versões do jogo com três ou mais campos de batalha.
Além de aplicativos de estratégia militar, o jogo Coronel Blotto tem aplicativos de estratégia política (alocação de recursos em campos de batalha políticos), defesa de rede, corridas de patentes de P&D e decisões estratégicas de contratação. Considere duas equipes esportivas com limites orçamentários obrigatórios (ou dois departamentos de Economia com subsídios do tipo use ou perca) que buscam o mesmo conjunto de candidatos e precisam decidir entre muitas ofertas modestas ou uma busca agressiva de um subconjunto de candidatos.
Exemplo
Como um exemplo de jogo Blotto, considere o jogo em que dois jogadores escrevem cada um três inteiros positivos em ordem não decrescente e de forma que eles somam um número pré-especificado S. Subseqüentemente, os dois jogadores mostram um ao outro seus escritos, e compare os números correspondentes. O jogador que tiver dois números a mais que os correspondentes do adversário vence o jogo.
Para S = 6, apenas três escolhas de números são possíveis: (2, 2, 2), (1, 2, 3) e (1, 1, 4). É fácil ver que:
- Qualquer trigêmeo contra si mesmo é um empate
- (1, 1, 4) contra (1, 2, 3) é um empate
- (1, 2, 3) contra (2, 2, 2) é um empate
- (2, 2, 2) batidas (1, 1, 4)
Segue-se que a estratégia ótima é (2, 2, 2), pois ela não tem um desempenho pior do que empatar com qualquer outra estratégia enquanto derrota outra estratégia. No entanto, existem vários equilíbrios de Nash. Se ambos os jogadores escolherem a estratégia (2, 2, 2) ou (1, 2, 3), nenhum deles poderá vencer o outro mudando de estratégia, portanto, cada par de estratégia é um equilíbrio de Nash .
Para S maiores, o jogo torna-se progressivamente mais difícil de analisar. Para S = 12, pode-se mostrar que (2, 4, 6) representa a estratégia ótima, enquanto para S> 12, as estratégias determinísticas falham em ser ótimas. Para S = 13, escolher (3, 5, 5), (3, 3, 7) e (1, 5, 7) com probabilidade 1/3 cada pode ser mostrado como a estratégia probabilística ótima.
O jogo do Borel é semelhante ao exemplo acima para S muito grande, mas os jogadores não estão limitados a inteiros redondos. Portanto, eles têm um número infinito de estratégias puras disponíveis, na verdade, um continuum.
Este conceito também é implementado em uma história de Sun Bin ao assistir a uma corrida de carruagem com três corridas diferentes correndo ao mesmo tempo. Nas corridas, cada grupo tinha a opção de ter uma equipe de carruagem em cada corrida, e cada um escolheu usar uma estratégia de 1, 2, 3 (com 3 sendo a carruagem mais rápida e 1 sendo a mais lenta) para posicionar suas carruagens entre as três corridas criando vitórias apertadas em cada corrida e poucos resultados seguros sobre os vencedores. Quando questionado sobre como vencer, Sun Bin aconselhou o dono da carruagem a mudar seu posicionamento para 2, 3, 1. Embora ele com certeza perderia a corrida contra as carruagens mais rápidas (as 3 carruagens); ele venceria cada uma das outras corridas, com suas 3 carruagens vencendo facilmente 2 carruagens e sua 2 carruagem vencendo 1 carruagem.
Aplicativo
Este jogo é comumente usado como uma metáfora para a competição eleitoral, com dois partidos políticos dedicando dinheiro ou recursos para atrair o apoio de um número fixo de eleitores. Cada eleitor é um "campo de batalha" que pode ser vencido por um ou outro partido. O mesmo jogo também encontra aplicação na teoria do leilão, em que os licitantes devem fazer lances simultâneos.
Várias variações do jogo original foram resolvidas por Jean-François Laslier , Brian Roberson e Dmitriy Kvasov.
Veja também
Referências
links externos
- Arquivos secretos do coronel Blotto: Raciocínio iterativo multidimensional em ação por Ayala Arad e Ariel Rubinstein
- Jonathan Partington 's página Coronel Blotto