Função booleana - Boolean function

Em matemática , uma função booleana é uma função cujos argumentos e resultados assumem valores de um conjunto de dois elementos (geralmente {verdadeiro, falso}, {0,1} ou {-1,1}). Nomes alternativos são função de comutação , usada especialmente na literatura da ciência da computação mais antiga, e função de verdade (ou função lógica) , usada em lógica . As funções booleanas são o assunto da álgebra booleana e da teoria de comutação .

Uma função booleana assume a forma , onde é conhecida como domínio booleano e é um número inteiro não negativo chamado aridade da função. No caso em que , a "função" é um elemento constante de . Uma função booleana com várias saídas, com uma função booleana vetorial ou com valor vetorial (uma S-box na criptografia ). ${\ displaystyle f: \ {0,1 \} ^ {k} \ to \ {0,1 \}}$${\ displaystyle \ {0,1 \}}$${\ displaystyle k}$${\ displaystyle k = 0}$${\ displaystyle \ {0,1 \}}$${\ displaystyle f: \ {0,1 \} ^ {k} \ to \ {0,1 \} ^ {m}}$${\ displaystyle m> 1}$

Existem diferentes funções booleanas com argumentos; igual ao número de tabelas verdade diferentes com entradas. ${\ displaystyle 2 ^ {2 ^ {k}}}$${\ displaystyle k}$${\ displaystyle 2 ^ {k}}$

Cada função booleana -ary pode ser expressa como uma fórmula proposicional em variáveis , e duas fórmulas proposicionais são logicamente equivalentes se e somente se expressarem a mesma função booleana. ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle x_ {1}, ..., x_ {k}}$

Exemplos

As funções booleanas simétricas rudimentares ( conectivos lógicos ou portas lógicas ) são:

• NOT , negação ou complemento - que recebe uma entrada e retorna verdadeiro quando a entrada é falsa ("não")

• AND ou conjunção - verdadeiro quando todas as entradas são verdadeiras ("ambos")

• OU ou disjunção - verdadeiro quando qualquer entrada for verdadeira ("qualquer um")

• XOR ou disjunção exclusiva - verdadeiro quando uma de suas entradas é verdadeira e a outra é falsa ("diferente")

• Traço NAND ou Sheffer - verdadeiro quando não é o caso de todas as entradas serem verdadeiras ("não ambos")
• NOR ou lógico nem - verdadeiro quando nenhuma das entradas é verdadeira ("nenhum")
• XNOR ou igualdade lógica - verdadeiro quando ambas as entradas são iguais ("igual")

Um exemplo de função mais complicada é a função majoritária (de um número ímpar de entradas).

Representação

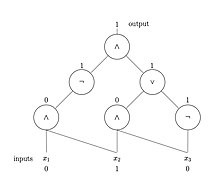
Uma função booleana pode ser especificada de várias maneiras:

• Tabela verdade : listando explicitamente seu valor para todos os valores possíveis dos argumentos
  • Diagrama de Marquand: valores da tabela verdade organizados em uma grade bidimensional (usada em um mapa de Karnaugh )
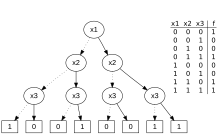
  • Diagrama de decisão binária , listando os valores da tabela verdade na parte inferior de uma árvore binária
  • Diagrama de Venn , representando os valores da tabela verdade como uma coloração das regiões do plano

Algebricamente, como uma fórmula proposicional usando funções booleanas rudimentares:

• Forma normal de negação , uma combinação arbitrária de AND e OR dos argumentos e seus complementos
• Forma normal disjuntiva , como um OR de ANDs dos argumentos e seus complementos
• Forma normal conjuntiva , como um AND de ORs dos argumentos e seus complementos
• Forma normal canônica , uma fórmula padronizada que identifica exclusivamente a função:
  • Forma normal algébrica ou polinômio de Zhegalkin , como um XOR de ANDs dos argumentos (sem complementos permitidos)
  • Forma normal disjuntiva completa (canônica) , um OR de ANDs contendo cada argumento ou complemento ( mintermos )
  • Forma normal conjuntiva completa (canônica) , um AND de ORs, cada um contendo cada argumento ou complemento ( maxtermos )
  • Forma canônica de Blake , o OR de todos os implicantes principais da função

As fórmulas booleanas também podem ser exibidas como um gráfico:

• Gráfico acíclico direcionado proposicional
  • Diagrama de circuito digital de portas lógicas , um circuito booleano
  • Gráfico do inversor E , usando apenas AND e NOT

Para otimizar os circuitos eletrônicos, as fórmulas booleanas podem ser minimizadas usando o algoritmo Quine-McCluskey ou o mapa de Karnaugh .

Análise

Propriedades

Uma função booleana pode ter uma variedade de propriedades:

• Constante : é sempre verdadeiro ou sempre falso, independentemente de seus argumentos.
• Monótono : para cada combinação de valores de argumento, alterar um argumento de falso para verdadeiro só pode fazer com que a saída mude de falso para verdadeiro e não de verdadeiro para falso. Uma função é considerada unada em uma determinada variável se for monótona em relação às mudanças nessa variável.
• Linear : para cada variável, inverter o valor da variável sempre faz diferença no valor verdade ou nunca faz diferença (uma função de paridade ).
• Simétrico : o valor não depende da ordem de seus argumentos.
• Ler uma vez : pode ser expresso com conjunção , disjunção e negação com uma única instância de cada variável.
• Equilibrado : se sua tabela verdade contém uma quantidade igual de zeros e uns. O peso de Hamming da função é o número de unidades na tabela verdade.
• Dobrado : seus derivados são todos balanceados (o espectro de autocorrelação é zero)
• Correlação imune à ordem m : se a saída não estiver correlacionada com todas as combinações (lineares) de no máximo m argumentos
• Evasivo : se a avaliação da função sempre requer o valor de todos os argumentos
• Uma função booleana é uma função Sheffer se ela pode ser usada para criar (por composição) qualquer função booleana arbitrária (ver completude funcional )
• O grau algébrico de uma função é a ordem do monômio de ordem superior em sua forma algébrica normal

A complexidade do circuito tenta classificar as funções booleanas com relação ao tamanho ou profundidade dos circuitos que podem computá-las.

Funções derivadas

Uma função booleana podem ser decompostos usando o teorema de expansão de Boole em positivos e negativos Shannon cofactores ( expansão Shannon ), que são os (k-1) funções -ary resultantes da fixação um dos argumentos para (zero ou um). As funções gerais (k-árias) obtidas pela imposição de uma restrição linear em um conjunto de entradas (um subespaço linear) são conhecidas como subfunções .

A derivada booleana da função para um dos argumentos é uma função (k-1) -ary que é verdadeira quando a saída da função é sensível à variável de entrada escolhida; é o XOR dos dois cofatores correspondentes. Um derivado e um co-fator são usados ​​em uma expansão de Reed-Muller . O conceito pode ser generalizado como uma derivada k-ária na direção dx, obtida como a diferença (XOR) da função em x e x + dx.

A transformada de Möbius (ou transformada de Boole-Möbius ) de uma função booleana é o conjunto de coeficientes de seu polinômio ( forma normal algébrica ), em função dos vetores expoentes monomiais. É uma transformação autoinversa . Ele pode ser calculado de forma eficiente usando um algoritmo de borboleta (" Fast Möbius Transform "), análogo à Fast Fourier Transform . As funções booleanas coincidentes são iguais a suas transformadas de Möbius, ou seja, seus valores de tabela verdade (mintermo) são iguais a seus coeficientes algébricos (monomiais). Existem 2 ^ 2 ^ ( k −1) funções coincidentes de k argumentos.

Análise criptográfica

A transformada de Walsh de uma função booleana é uma função de valor inteiro k-ário que fornece os coeficientes de uma decomposição em funções lineares ( funções de Walsh ), análoga à decomposição de funções de valor real em harmônicos pela transformada de Fourier . Seu quadrado é o espectro de potência ou espectro de Walsh . O coeficiente de Walsh de um único vetor de bit é uma medida para a correlação desse bit com a saída da função booleana. O coeficiente de Walsh máximo (em valor absoluto) é conhecido como linearidade da função. O maior número de bits (ordem) para o qual todos os coeficientes de Walsh são 0 (ou seja, as subfunções são balanceadas) é conhecido como resiliência , e a função é considerada uma correlação imune a essa ordem. Os coeficientes de Walsh desempenham um papel fundamental na criptoanálise linear .

A autocorrelação de uma função booleana é uma função de valor inteiro k-ário que fornece a correlação entre um certo conjunto de mudanças nas entradas e a saída da função. Para um determinado vetor de bits, ele está relacionado ao peso de Hamming da derivada nessa direção. O coeficiente de autocorrelação máximo (em valor absoluto) é conhecido como indicador absoluto . Se todos os coeficientes de autocorrelação são 0 (isto é, as derivadas são balanceadas) para um certo número de bits, diz-se que a função satisfaz o critério de propagação para aquela ordem; se forem todos zero, a função é uma função dobrada . Os coeficientes de autocorrelação desempenham um papel fundamental na criptoanálise diferencial .

Os coeficientes de Walsh de uma função booleana e seus coeficientes de autocorrelação são relacionados pelo equivalente do teorema de Wiener-Khinchin , que afirma que a autocorrelação e o espectro de potência são um par de transformada de Walsh.

Esses conceitos podem ser estendidos naturalmente para funções booleanas vetoriais considerando seus bits de saída ( coordenadas ) individualmente, ou mais profundamente, olhando para o conjunto de todas as funções lineares de bits de saída, conhecidas como seus componentes . O conjunto de Walsh transformações dos componentes é conhecida como uma mesa aproximação linear (LAT) ou matriz de correlação ; ele descreve a correlação entre diferentes combinações lineares de bits de entrada e saída. O conjunto de coeficientes de autocorrelação dos componentes é a tabela de autocorrelação , relacionada por uma transformação de Walsh dos componentes à Tabela de Distribuição de Diferença (DDT) mais amplamente usada que lista as correlações entre as diferenças nos bits de entrada e saída (ver também: S-box )

Forma polinomial real

No hipercubo da unidade

Qualquer função booleana pode ser estendida de forma única (interpolados) para o domínio real por um polinômio multilinear em , construído pela soma dos valores da tabela de verdade multiplicado por polinômios indicador :${\ displaystyle f (x): \ {0,1 \} ^ {n} \ rightarrow \ {0,1 \}}$${\ displaystyle \ mathbb {R} ^ {n}}$

Por exemplo, a extensão da função binária XOR é${\ displaystyle x \ oplus y}$que é igual aAlguns outros exemplos são negação ( ), AND ( ) e OR ( ). Quando todos os operandos são independentes (não compartilham variáveis), a forma polinomial de uma função pode ser encontrada aplicando repetidamente os polinômios dos operadores em uma fórmula booleana. Quando os coeficientes são calculados módulo 2 obtém-se a forma normal algébrica ( polinômio de Zhegalkin ). ${\ displaystyle 1-x}$${\ displaystyle xy}$${\ displaystyle x + y-xy}$

Expressões diretas para os coeficientes do polinômio podem ser derivadas tomando uma derivada apropriada:

$${\ displaystyle {\ begin {array} {lcl} f ^ {*} (00) & = & (f ^ {*}) (00) & = & f (00) \\ f ^ {*} (01) & = & (\ parcial _ {1} f ^ {*}) (00) & = & - f (00) + f (01) \\ f ^ {*} (10) & = & (\ parcial _ {2 } f ^ {*}) (00) & = & - f (00) + f (10) \\ f ^ {*} (11) & = & (\ parcial _ {1} \ parcial _ {2} f ^ {*}) (00) & = & f (00) -f (01) -f (10) + f (11) \\\ end {array}}}$$

isso se generaliza como a inversão de Möbius do conjunto parcialmente ordenado de vetores de bits:

$${\ displaystyle f ^ {*} (m) = \ sum _ {a \ subseteq m} (- 1) ^ {| a | + | m |} f (a)}$$

onde denota o peso do vetor de bits . Tomado o módulo 2, esta é a transformada Booleana de Möbius , fornecendo os coeficientes da forma normal algébrica :${\ displaystyle | a |}$${\ displaystyle a}$

$${\ displaystyle {\ hat {f}} (m) = \ bigoplus _ {a \ subseteq m} f (a)}$$

Em ambos os casos, a soma é feita sobre todos os vetores de bits a cobertos por m , isto é, os bits "um" de a formam um subconjunto dos bits um de m .

Quando o domínio é restrito ao hipercubo n-dimensional , o polinômio dá a probabilidade de um resultado positivo quando a função booleana

f é aplicada a n variáveis aleatórias independentes ( Bernoulli ), com probabilidades individuais x . Um caso especial desse fato é o lema de empilhamento para funções de paridade . A forma polinomial de uma função booleana também pode ser usada como sua extensão natural para a lógica fuzzy . ${\ displaystyle [0,1] ^ {n}}$${\ displaystyle f ^ {*} (x): [0,1] ^ {n} \ rightarrow [0,1]}$

No hipercubo simétrico

Freqüentemente, o domínio booleano é considerado como , com mapeamento falso ("0") para 1 e verdadeiro ("1") para -1 (consulte

Análise de funções booleanas ). O polinômio correspondente a é então dado por:${\ displaystyle \ {- 1,1 \}}$${\ displaystyle g (x): \ {- 1,1 \} ^ {n} \ rightarrow \ {- 1,1 \}}$

$${\ displaystyle g ^ {*} (x) = \ sum _ {a \ in {\ {- 1,1 \}} ^ {n}} g (a) \ prod _ {i: a_ {i} = - 1} {\ frac {1-x_ {i}} {2}} \ prod _ {i: a_ {i} = 1} {\ frac {1 + x_ {i}} {2}}}$$

Usar o domínio booleano simétrico simplifica certos aspectos da análise , uma vez que a negação corresponde à multiplicação por -1 e as funções lineares são monômios (XOR é multiplicação). Essa forma polinomial corresponde, portanto, à transformação de Walsh (neste contexto também conhecida como transformação de Fourier ) da função (veja acima). O polinômio também tem a mesma interpretação estatística que aquele no domínio booleano padrão, exceto que agora ele lida com os valores esperados (consulte o lema de empilhamento para um exemplo). ${\ displaystyle E (X) = P (X = 1) -P (X = -1) \ in [-1,1]}$

Formulários

As funções booleanas desempenham um papel fundamental em questões de teoria da

complexidade , bem como no projeto de processadores para computadores digitais , onde são implementadas em circuitos eletrônicos usando portas lógicas .

As propriedades das funções booleanas são críticas em criptografia , particularmente no projeto de algoritmos de chave simétrica (consulte a caixa de substituição ).

Na teoria dos jogos cooperativos , as funções booleanas monótonas são chamadas de jogos simples (jogos de votação); esta noção é aplicada para resolver problemas na teoria da escolha social .

Veja também

• Função pseudo-booleana
• Função com valor booleano
• Tópicos de álgebra booleana
• Álgebra de Conjuntos
• Modelo de árvore de decisão
• Função de indicador
• Conjunto assinado

Referências

Leitura adicional

• Crama, Yves; Hammer, Peter L. (2011), Boolean Functions: Theory, Algorithms, and Applications , Cambridge University Press, doi : 10.1017 / CBO9780511852008 , ISBN 9780511852008
• "Boolean function" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Janković, Dragan; Stanković, Radomir S .; Moraga, Claudio (novembro de 2003). "Otimização de expressões aritméticas usando propriedade de dupla polaridade" . Serbian Journal of Electrical Engineering . 1 (71–80, número 1): 71–80. doi : 10.2298 / SJEE0301071J .
• Arnold, Bradford Henry (1 de janeiro de 2011). Lógica e Álgebra Booleana . Courier Corporation. ISBN 978-0-486-48385-6.
• Mano, MM; Ciletti, MD (2013), Digital Design , Pearson