
Um conjunto (em azul claro) e seus limites (em azul escuro).
Na topologia e matemática em geral, o limite de um subconjunto S de um espaço topológico X é o conjunto de pontos que podem ser abordados a partir de ambos S e do lado de fora de S . Mais precisamente, é o conjunto de pontos no fechamento de não pertencer ao interior de Um elemento da fronteira de é chamado de ponto de fronteira de. O termo operação de fronteira refere-se a encontrar ou tomar a fronteira de um conjunto. Notações usadas para limite de um conjunto incluem e Alguns autores (por exemplo, Willard, em Topologia geral ) usam o termo fronteira em vez de limite em uma tentativa de evitar confusão com uma definição diferente usada na topologia algébrica e na teoria das variedades . Apesar da ampla aceitação do significado dos termos limite e fronteira, eles às vezes têm sido usados para se referir a outros conjuntos. Por exemplo, espaços métricos por ET Copson utiliza o termo limite para se referir a Hausdorff da fronteira , o que é definido como a intersecção de um conjunto com o seu limite. Hausdorff também introduziu o termo resíduo , que é definido como a interseção de um conjunto com o fechamento da borda de seu complemento.







Um componente conectado do limite de é chamado de componente do limite de

Definições comuns
Existem várias definições equivalentes para o limite de um subconjunto de um espaço topológico que será denotado por ou simplesmente se for compreendido:






- É o fechamento de menos o interior de em :




onde denota o fechamento de em e denota o interior topológico de em





- É a intersecção do fechamento de com o fechamento de seu complemento :


- É o conjunto de pontos de modo que cada vizinhança de contém pelo menos um ponto de e pelo menos um ponto que não é de :





Um ponto limite de um conjunto refere-se a qualquer elemento do limite desse conjunto. O limite definido acima é às vezes chamado de limite topológico do conjunto para distingui-lo de outras noções com nomes semelhantes, como o limite de um manifold com limite ou o limite de um manifold com cantos , para citar apenas alguns exemplos.

Propriedades
O fechamento de um conjunto é igual à união do conjunto com seu limite:


onde denota o
fechamento de em
Um conjunto é fechado se e somente se contiver seu limite, e aberto se e somente se for separado de seu limite. A fronteira de um conjunto está fechada ; isso segue da fórmula que expressa como a interseção de dois subconjuntos fechados de





("Tricotomia")Dado qualquer subconjunto, cada ponto encontra-se em exatamente um dos três conjuntos e dito de forma diferente,




e esses três conjuntos são disjuntos aos pares . Consequentemente, se esses conjuntos não estiverem vazios, eles formam uma partição de
Um ponto é um ponto limite de um conjunto se e somente se cada vizinhança de contiver pelo menos um ponto no conjunto e pelo menos um ponto que não esteja no conjunto. O limite do interior de um conjunto, bem como o limite do fechamento de um conjunto, estão ambos contidos no limite do conjunto.


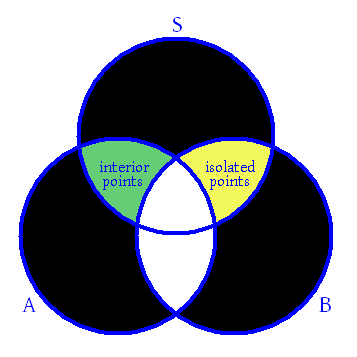
Diagrama de Venn conceitual mostrando as relações entre os diferentes pontos de um subconjunto de = conjunto de pontos limites do conjunto de pontos de fronteira da área sombreada em verde = conjunto de pontos internos da área sombreada em amarelo = conjunto de pontos isolados de áreas sombreadas em preto = conjuntos vazios. Cada ponto de é um ponto interno ou um ponto limite. Além disso, cada ponto de é um ponto de acumulação ou um ponto isolado. Da mesma forma, cada ponto limite de é um ponto de acumulação ou um ponto isolado. Os pontos isolados são sempre pontos de fronteira.










Exemplos
Caracterizações e exemplos gerais
O limite de um conjunto é igual ao limite do complemento do conjunto:

Se é um subconjunto denso e aberto de então


O interior da fronteira de um conjunto fechado é o conjunto vazio. Conseqüentemente, o interior da fronteira do fechamento de um conjunto é o conjunto vazio. O interior da fronteira de um conjunto aberto também é o conjunto vazio. Conseqüentemente, o interior da fronteira do interior de um conjunto é o conjunto vazio. Em particular, se for um subconjunto fechado ou aberto de então não existe nenhum subconjunto não vazio , que também seja um subconjunto aberto de
Este fato é importante para a definição e uso de subconjuntos densos em nenhum lugar , subconjuntos escassos e espaços de Baire .





Um conjunto é o limite de algum conjunto aberto se, e somente se, for fechado e em nenhum lugar denso . O limite de um conjunto está vazio se e somente se o conjunto for fechado e aberto (ou seja, um conjunto clopen ).
Exemplos concretos
Considere a linha real com a topologia usual (ou seja, a topologia cujos conjuntos de base são intervalos abertos ) e o subconjunto de números racionais (cujo interior topológico em está vazio). Então



![{\ displaystyle \ parcial (0,5) = \ parcial [0,5) = \ parcial (0,5] = \ parcial [0,5] = \ {0,5 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84d5dd08b8ce4a5959c14f806036b74dda17723a)


![{\ displaystyle \ partial (\ mathbb {Q} \ cap [0,1]) = [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/992baab3b186c92f1b758497f0437ae600af6c5c)
Esses dois últimos exemplos ilustram o fato de que o limite de um conjunto denso com interior vazio é o seu fechamento. Eles também mostram que é possível que o limite de um subconjunto contenha um subconjunto aberto não vazio de ; isto é, para o interior de in ser não vazio. No entanto, o limite de um subconjunto fechado sempre tem um interior vazio.





No espaço dos números racionais com a topologia usual (a topologia do subespaço de ), a fronteira de onde é irracional está vazia.



O limite de um conjunto é uma noção topológica e pode mudar se alguém alterar a topologia. Por exemplo, dada a topologia usual no limite de um disco fechado é o círculo ao redor do disco: Se o disco é visto como um conjunto com sua própria topologia usual, isto é, o limite do disco é o próprio disco: Se o disco é visto como seu próprio espaço topológico (com a topologia de subespaço de ), então o limite do disco está vazio.







Limite de uma bola aberta vs. sua esfera circundante
Este exemplo demonstra que o limite topológico de uma bola de raio aberta não é necessariamente igual à esfera de raio correspondente (centrada no mesmo ponto); também mostra que o fechamento de uma bola de raio aberta não é necessariamente igual ao de uma bola de raio fechada (novamente centrada no mesmo ponto). Denotar a habitual métrica Euclidiana em pelo






que induz na
topologia euclidiana usual . Deixe denotar a união do -eixo com o círculo unitário centrado na origem ; isto é, que é um subespaço topológica de cuja topologia é igual a que induzida pela (limitação) da métrica
Em particular, os conjuntos e são todos os subconjuntos fechados de e subconjuntos assim também fechadas da sua subespaço
Daqui em diante, a menos que claramente indicado de outro modo , toda bola aberta, bola fechada e esfera deve ser assumida como centrada na origem e, além disso, apenas o espaço métrico será considerado (e não seu superespaço ); este ser um conectado-path e conectado-path localmente espaço completo .










![{\ displaystyle \ {0 \} \ times [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3278f4a9ff634e32edeb1039a7687ef077566e)





Denote a bola de raio aberta em por
para que quando então





é o subintervalo aberto do -eixo estritamente entre e
A esfera unitária em ("unidade" significa que seu raio é ) é






enquanto a esfera unitária fechada é a união da esfera unitária aberta e da esfera unitária centrada neste mesmo ponto:

![{\ displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ direita).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbbdb5bb903d77c3b2b46a464186540e9f2146ed)
No entanto, a fronteira topológica encerramento e topológica no da bola unidade aberta são:




![{\ displaystyle \ partial _ {X} B_ {1} = \ {(0,1), (0, -1) \} \ quad {\ text {and}} \ quad \ operatorname {cl} _ {X} B_ {1} ~ = ~ B_ {1} \ xícara \ parcial _ {X} B_ {1} ~ = ~ B_ {1} \ xícara \ {(0,1), (0, -1) \} ~ = ~ \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2df64b6756937f1c40bb722992413fe99c747e7b)
Em particular, o limite topológico da bola unitária aberta é um subconjunto próprio da esfera unitária em
E o fechamento topológico da bola unitária aberta é um subconjunto apropriado da bola unitária fechada em
O ponto, por exemplo, não pode pertencer porque não existe uma sequência em que converge para ele; o mesmo raciocínio generaliza para explicar também por que nenhum ponto fora do subintervalo fechado pertence a Porque o limite topológico do conjunto é sempre um subconjunto de fechamento de, segue-se que também deve ser um subconjunto de



![{\ displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ direita)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84ca278fa188aca7582438f63a8eb555344f5719)





![{\ displaystyle \ {0 \} \ times [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3278f4a9ff634e32edeb1039a7687ef077566e)




![{\ displaystyle \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd9bfe3c9b6013059a0365209b818ee5b8d406)
Em qualquer espaço métrico, o limite topológico de uma bola aberta de raio centrada em um ponto é sempre um subconjunto da esfera de raio centrada nesse mesmo ponto ; isso é,







sempre se mantém.
Além disso, a esfera unitária em contém, que é um subconjunto aberto de. Isso mostra, em particular, que a esfera unitária em contém um subconjunto
aberto não vazio de





Limite de um limite
Para qualquer conjunto, onde denota o
superconjunto com igualdade mantida se e somente se o limite de não tiver pontos internos, o que será o caso, por exemplo, se for fechado ou aberto. Como a fronteira de um conjunto é fechada, para qualquer conjunto O operador de fronteira satisfaz um tipo enfraquecido de idempotência .






Ao discutir as fronteiras de variedades ou simplexes e seus complexos simpliciais , frequentemente encontramos a afirmação de que a fronteira da fronteira está sempre vazia. De fato, a construção da homologia singular se apóia criticamente nesse fato. A explicação para a aparente incongruência é que a fronteira topológica (o assunto deste artigo) é um conceito ligeiramente diferente da fronteira de uma variedade ou de um complexo simplicial. Por exemplo, o limite de um disco aberto visto como uma variedade está vazio, assim como seu limite topológico visto como um subconjunto de si mesmo, enquanto seu limite topológico visto como um subconjunto do plano real é o círculo ao redor do disco. Por outro lado, o limite de um disco fechado visto como uma variedade é o círculo delimitador, assim como seu limite topológico visto como um subconjunto do plano real, enquanto seu limite topológico visto como um subconjunto de si mesmo está vazio. Em particular, o limite topológico depende do espaço ambiente, enquanto o limite de uma variedade é invariante.
Veja também
Notas
Citações
Referências






































![{\ displaystyle \ parcial (0,5) = \ parcial [0,5) = \ parcial (0,5] = \ parcial [0,5] = \ {0,5 \}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84d5dd08b8ce4a5959c14f806036b74dda17723a)


![{\ displaystyle \ partial (\ mathbb {Q} \ cap [0,1]) = [0,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/992baab3b186c92f1b758497f0437ae600af6c5c)





















![{\ displaystyle \ {0 \} \ times [-1,1]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6a3278f4a9ff634e32edeb1039a7687ef077566e)









![{\ displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ direita).}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbbdb5bb903d77c3b2b46a464186540e9f2146ed)



![{\ displaystyle \ partial _ {X} B_ {1} = \ {(0,1), (0, -1) \} \ quad {\ text {and}} \ quad \ operatorname {cl} _ {X} B_ {1} ~ = ~ B_ {1} \ xícara \ parcial _ {X} B_ {1} ~ = ~ B_ {1} \ xícara \ {(0,1), (0, -1) \} ~ = ~ \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2df64b6756937f1c40bb722992413fe99c747e7b)



![{\ displaystyle \ left \ {p \ in X: d (p, \ mathbf {0}) \ leq 1 \ right \} = S ^ {1} \ cup \ left (\ {0 \} \ times [-1 , 1] \ direita)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/84ca278fa188aca7582438f63a8eb555344f5719)


![{\ displaystyle \ {0 \} \ times [-1,1].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/50bd9bfe3c9b6013059a0365209b818ee5b8d406)









