Algoritmo de linha de Bresenham - Bresenham's line algorithm

O algoritmo de linha de Bresenham é um algoritmo de desenho de linha que determina os pontos de um raster n- dimensional que deve ser selecionado para formar uma aproximação de uma linha reta entre dois pontos . É comumente usado para desenhar linhas primitivas em uma imagem bitmap (por exemplo, na tela de um computador ), pois usa apenas adição, subtração e deslocamento de bits inteiros , todas operações muito baratas em arquiteturas de computador padrão . É um algoritmo de erro incremental . É um dos primeiros algoritmos desenvolvidos no campo da computação gráfica . Uma extensão do algoritmo original pode ser usada para desenhar círculos .

Embora algoritmos como o algoritmo de Wu também sejam freqüentemente usados ​​na computação gráfica moderna porque podem suportar anti-serrilhamento , a velocidade e a simplicidade do algoritmo de linha de Bresenham significa que ele ainda é importante. O algoritmo é usado em hardware, como plotadoras e nos chips gráficos de placas de vídeo modernas . Ele também pode ser encontrado em muitas bibliotecas de gráficos de software . Como o algoritmo é muito simples, ele geralmente é implementado no firmware ou no hardware gráfico de placas de vídeo modernas .

O rótulo "Bresenham" é usado hoje para uma família de algoritmos que estendem ou modificam o algoritmo original de Bresenham.

História

O algoritmo de linha de Bresenham recebeu o nome de Jack Elton Bresenham, que o desenvolveu em 1962 na IBM . Em 2001, Bresenham escreveu:

Eu estava trabalhando no laboratório de computação do laboratório de desenvolvimento da IBM em San Jose. Um plotter Calcomp foi conectado a um IBM 1401 por meio do console da máquina de escrever 1407. [O algoritmo] estava em uso em produção no verão de 1962, possivelmente um mês ou mais antes. Naquela época, os programas eram trocados livremente entre as empresas, de modo que a Calcomp (Jim Newland e Calvin Hefte) tinha cópias. Quando voltei para Stanford no outono de 1962, coloquei uma cópia na biblioteca do Stanford Comp Center. Uma descrição da rotina de desenho de linhas foi aceita para apresentação na convenção nacional ACM de 1963 em Denver, Colorado. Foi um ano em que não foram publicados anais, apenas pauta de palestrantes e temas em uma edição das Comunicações da ACM. Uma pessoa do IBM Systems Journal me perguntou depois de fazer minha apresentação se eles poderiam publicar o artigo. Eu concordei feliz e eles o imprimiram em 1965.

O algoritmo de Bresenham foi estendido para produzir círculos, elipses, curvas bézier cúbicas e quadráticas, bem como versões nativas com suavização de serrilhado.

Método

Ilustração do resultado do algoritmo de linha de Bresenham. (0,0) está no canto superior esquerdo da grade, (1,1) está na extremidade superior esquerda da linha e (11, 5) está na extremidade inferior direita da linha.

As seguintes convenções serão usadas:

• o canto superior esquerdo é (0,0) de modo que as coordenadas do pixel aumentem nas direções direita e para baixo (por exemplo, que o pixel em (7,4) está diretamente acima do pixel em (7,5)), e
• os centros dos pixels têm coordenadas inteiras.

Os pontos finais da linha são os pixels em e , onde a primeira coordenada do par é a coluna e a segunda é a linha. ${\ displaystyle (x_ {0}, y_ {0})}$${\ displaystyle (x_ {1}, y_ {1})}$

O algoritmo será apresentado inicialmente apenas para o octante em que o segmento desce e para a direita ( e ), e sua projeção horizontal é mais longa que a projeção vertical (a linha tem inclinação positiva menor que 1). Neste octante, para cada coluna x entre e , há exatamente uma linha y (calculada pelo algoritmo) contendo um pixel da linha, enquanto cada linha entre e pode conter vários pixels rasterizados. ${\ displaystyle x_ {0} \ leq x_ {1}}$${\ displaystyle y_ {0} \ leq y_ {1}}$${\ displaystyle x_ {1} -x_ {0}}$${\ displaystyle y_ {1} -y_ {0}}$${\ displaystyle x_ {0}}$${\ displaystyle x_ {1}}$${\ displaystyle y_ {0}}$${\ displaystyle y_ {1}}$

O algoritmo de Bresenham escolhe o inteiro y correspondente ao centro do pixel que está mais próximo do y ideal (fracionário) para o mesmo x ; em colunas sucessivas y pode permanecer o mesmo ou aumentar em 1. A equação geral da linha através dos pontos finais é dada por:

${\ displaystyle {\ frac {y-y_ {0}} {y_ {1} -y_ {0}}} = {\ frac {x-x_ {0}} {x_ {1} -x_ {0}}} }$.

Como sabemos a coluna, x , a linha do pixel, y , é dada arredondando essa quantidade para o número inteiro mais próximo:

${\ displaystyle y = {\ frac {y_ {1} -y_ {0}} {x_ {1} -x_ {0}}} (x-x_ {0}) + y_ {0}}$.

A inclinação depende apenas das coordenadas do ponto final e pode ser pré-computada, e o y ideal para valores inteiros sucessivos de x pode ser calculado começando e adicionando repetidamente a inclinação. ${\ displaystyle (y_ {1} -y_ {0}) / (x_ {1} -x_ {0})}$${\ displaystyle y_ {0}}$

Na prática, o algoritmo não acompanha a coordenada y, que aumenta em m = ∆y / ∆x cada vez que x aumenta em um; ele mantém um limite de erro em cada estágio, que representa o negativo da distância de (a) o ponto onde a linha sai do pixel até (b) a borda superior do pixel. Este valor é primeiro definido como (devido ao uso das coordenadas centrais do pixel) e é incrementado em m cada vez que a coordenada x é incrementada em um. Se o erro se tornar maior que 0,5 , sabemos que a linha se moveu um pixel para cima e que devemos incrementar nossa coordenada y e reajustar o erro para representar a distância do topo do novo pixel - o que é feito subtraindo um de erro. ${\ displaystyle y_ {0} -0,5}$

Derivação

Para derivar o algoritmo de Bresenham, duas etapas devem ser executadas. O primeiro passo é transformar a equação de uma linha da forma típica de interceptação em declive em algo diferente; e então usar essa nova equação para traçar uma linha com base na ideia de acúmulo de erro.

Equação linear

y = f (x) =. 5x + 1 ou f (x, y) = x-2y + 2

Meios planos positivos e negativos

A forma de declive-interceptação de uma linha é escrita como

${\ displaystyle y = f (x) = mx + b}$

onde m é a inclinação eb é a interceptação y. Esta é uma função de apenas x e seria útil fazer esta equação escrita como uma função de x e y. Usando manipulação algébrica e reconhecimento de que a inclinação é a "subida sobre a corrida" ou então ${\ displaystyle \ Delta y / \ Delta x}$

${\ displaystyle {\ begin {alinhados} y & = mx + b \\ y & = {\ frac {(\ Delta y)} {(\ Delta x)}} x + b \\ (\ Delta x) y & = (\ Delta y) x + (\ Delta x) b \\ 0 & = (\ Delta y) x - (\ Delta x) y + (\ Delta x) b \ end {alinhado}}}$

Deixando esta última equação ser uma função de xey, então ela pode ser escrita como

${\ displaystyle f (x, y) = 0 = Ax + By + C}$

onde as constantes estão

• ${\ displaystyle A = \ Delta y}$
• ${\ displaystyle B = - \ Delta x}$
• ${\ displaystyle C = (\ Delta x) b}$

A linha é então definida para algumas constantes A, B e C em qualquer lugar . Para qualquer um que não esteja na linha, então . Tudo sobre este formulário envolve apenas inteiros se xey forem inteiros, pois as constantes são necessariamente inteiros. ${\ displaystyle f (x, y) = 0}$${\ displaystyle (x, y)}$${\ displaystyle f (x, y) \ neq 0}$

Por exemplo, a linha então isso poderia ser escrito como . O ponto (2,2) está na linha ${\ displaystyle y = {\ frac {1} {2}} x + 1}$${\ displaystyle f (x, y) = x-2y + 2}$

${\ displaystyle f (2,2) = x-2y + 2 = (2) -2 (2) + 2 = 2-4 + 2 = 0}$

e o ponto (2,3) não está na linha

${\ displaystyle f (2,3) = (2) -2 (3) + 2 = 2-6 + 2 = -2}$

e nem é o ponto (2,1)

${\ displaystyle f (2,1) = (2) -2 (1) + 2 = 2-2 + 2 = 2}$

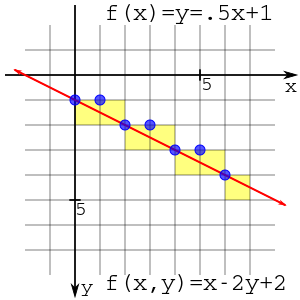
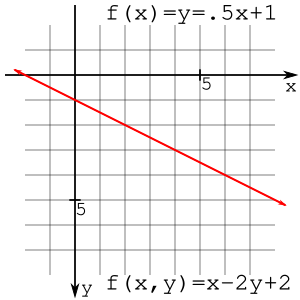
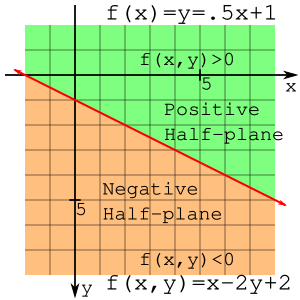
Observe que os pontos (2,1) e (2,3) estão em lados opostos da linha e f (x, y) é avaliado como positivo ou negativo. Uma linha divide um plano em metades e o semiplano que tem um f negativo (x, y) pode ser chamado de semiplano negativo e a outra metade pode ser chamada de semiplano positivo. Esta observação é muito importante no restante da derivação.

Algoritmo

Claramente, o ponto de partida está na linha

${\ displaystyle f (x_ {0}, y_ {0}) = 0}$

apenas porque a linha está definida para começar e terminar em coordenadas inteiras (embora seja inteiramente razoável querer desenhar uma linha com pontos finais não inteiros).

Ponto candidato (2,2) em azul e dois pontos candidatos em verde (3,2) e (3,3)

Tendo em mente que a inclinação é menor ou igual a um, o problema agora se apresenta se o próximo ponto deve ser em ou . Talvez intuitivamente, o ponto deva ser escolhido com base no que está mais próximo da linha em . Se estiver mais próximo do primeiro, inclua o primeiro ponto na linha, se o último, então o último. Para responder a isso, avalie a função de linha no ponto médio entre esses dois pontos: ${\ displaystyle (x_ {0} + 1, y_ {0})}$${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$${\ displaystyle x_ {0} +1}$

${\ displaystyle f (x_ {0} + 1, y_ {0} + {\ tfrac {1} {2}})}$

Se o valor disso for positivo, a linha ideal está abaixo do ponto médio e mais próxima do ponto candidato ; na verdade, a coordenada y avançou. Caso contrário, a linha ideal passa através ou acima do ponto médio e a coordenada y não avançou; neste caso, escolha o ponto . Essa observação é fundamental para entender! O valor da função de linha neste ponto médio é o único determinante de qual ponto deve ser escolhido. ${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$${\ displaystyle (x_ {0} + 1, y_ {0})}$

A imagem adjacente mostra o ponto azul (2,2) escolhido para estar na linha com dois pontos candidatos em verde (3,2) e (3,3). O ponto preto (3, 2,5) é o ponto médio entre os dois pontos candidatos.

Algoritmo para aritmética inteira

Alternativamente, a diferença entre os pontos pode ser usada em vez de avaliar f (x, y) nos pontos médios. Este método alternativo permite a aritmética apenas de inteiros, que geralmente é mais rápida do que usar a aritmética de ponto flutuante. Para derivar o método alternativo, defina a diferença como a seguir:

${\ displaystyle D = f (x_ {0} + 1, y_ {0} + {\ tfrac {1} {2}}) - f (x_ {0}, y_ {0})}$

Para a primeira decisão, esta formulação é equivalente ao método do ponto médio desde o ponto de partida. Simplificar essa expressão resulta em: ${\ displaystyle f (x_ {0}, y_ {0}) = 0}$

${\ displaystyle {\ begin {array} {rclcl} D & = & \ left [A (x_ {0} +1) + B \ left (y_ {0} + {\ frac {1} {2}} \ right) + C \ direita] & - & \ esquerda [Ax_ {0} + Por_ {0} + C \ direita] \\ & = & \ left [Ax_ {0} + Por_ {0} + C + A + {\ frac { 1} {2}} B \ right] & - & \ left [Ax_ {0} + By_ {0} + C \ right] \\ & = & A + {\ frac {1} {2}} B \ end {array }}}$

Assim como no método do ponto médio, se D for positivo, escolha , caso contrário, escolha . ${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$${\ displaystyle (x_ {0} + 1, y_ {0})}$

Se for escolhido, a mudança em D será: ${\ displaystyle (x_ {0} + 1, y_ {0})}$

${\ displaystyle {\ begin {array} {lclcl} \ Delta D & = & f (x_ {0} + 2, y_ {0} + {\ tfrac {1} {2}}) - f (x_ {0} +1 , y_ {0} + {\ tfrac {1} {2}}) & = & A & = & \ Delta y \\\ end {array}}}$

Se for escolhido, a mudança em D será: ${\ displaystyle (x_ {0} + 1, y_ {0} +1)}$

${\ displaystyle {\ begin {array} {lclcl} \ Delta D & = & f (x_ {0} + 2, y_ {0} + {\ tfrac {3} {2}}) - f (x_ {0} +1 , y_ {0} + {\ tfrac {1} {2}}) & = & A + B & = & \ Delta y- \ Delta x \ end {array}}}$

Se o novo D for positivo, então é escolhido, caso contrário . Esta decisão pode ser generalizada acumulando o erro em cada ponto subsequente. ${\ displaystyle (x_ {0} + 2, y_ {0} +1)}$${\ displaystyle (x_ {0} + 2, y_ {0})}$

Traçando a linha de (0,1) a (6,4) mostrando um gráfico de linhas de grade e pixels

Toda a derivação para o algoritmo é feita. Um problema de desempenho é o fator 1/2 no valor inicial de D. Como tudo isso é sobre o sinal da diferença acumulada, então tudo pode ser multiplicado por 2 sem consequência.

Isso resulta em um algoritmo que usa apenas aritmética de inteiros.

plotLine(x0, y0, x1, y1)
    dx = x1 - x0
    dy = y1 - y0
    D = 2*dy - dx
    y = y0

    for x from x0 to x1
        plot(x,y)
        if D > 0
            y = y + 1
            D = D - 2*dx
        end if
        D = D + 2*dy

Executar este algoritmo de (0,1) a (6,4) produz as seguintes diferenças com dx = 6 e dy = 3: ${\ displaystyle f (x, y) = x-2y + 2}$

D=2*3-6=0
Loop from 0 to 6
 * x=0: plot(0, 1), D≤0: D=0+6=6
 * x=1: plot(1, 1), D>0: D=6-12=-6, y=1+1=2, D=-6+6=0
 * x=2: plot(2, 2), D≤0: D=0+6=6
 * x=3: plot(3, 2), D>0: D=6-12=-6, y=2+1=3, D=-6+6=0
 * x=4: plot(4, 3), D≤0: D=0+6=6
 * x=5: plot(5, 3), D>0: D=6-12=-6, y=3+1=4, D=-6+6=0
 * x=6: plot(6, 4), D≤0: D=0+6=6

O resultado deste gráfico é mostrado à direita. A plotagem pode ser visualizada plotando na interseção das linhas (círculos azuis) ou preenchendo as caixas de pixel (quadrados amarelos). Independentemente disso, a plotagem é a mesma.

Todos os casos

No entanto, como mencionado acima, isso é apenas para o octante zero, ou seja, as linhas começando na origem com um gradiente entre 0 e 1, onde x aumenta em exatamente 1 por iteração ey aumenta em 0 ou 1.

O algoritmo pode ser estendido para cobrir gradientes entre 0 e -1, verificando se y precisa aumentar ou diminuir (ou seja, dy <0)

plotLineLow(x0, y0, x1, y1)
    dx = x1 - x0
    dy = y1 - y0
    yi = 1
    if dy < 0
        yi = -1
        dy = -dy
    end if
    D = (2 * dy) - dx
    y = y0

    for x from x0 to x1
        plot(x, y)
        if D > 0
            y = y + yi
            D = D + (2 * (dy - dx))
        else
            D = D + 2*dy
        end if

Ao alternar os eixos xey, uma implementação para gradientes íngremes positivos ou negativos pode ser escrita como

plotLineHigh(x0, y0, x1, y1)
    dx = x1 - x0
    dy = y1 - y0
    xi = 1
    if dx < 0
        xi = -1
        dx = -dx
    end if
    D = (2 * dx) - dy
    x = x0

    for y from y0 to y1
        plot(x, y)
        if D > 0
            x = x + xi
            D = D + (2 * (dx - dy))
        else
            D = D + 2*dx
        end if

Uma solução completa precisaria detectar se x1> x0 ou y1> y0 e reverter as coordenadas de entrada antes de desenhar, assim

plotLine(x0, y0, x1, y1)
    if abs(y1 - y0) < abs(x1 - x0)
        if x0 > x1
            plotLineLow(x1, y1, x0, y0)
        else
            plotLineLow(x0, y0, x1, y1)
        end if
    else
        if y0 > y1
            plotLineHigh(x1, y1, x0, y0)
        else
            plotLineHigh(x0, y0, x1, y1)
        end if
    end if

Em implementações de baixo nível que acessam a memória de vídeo diretamente, seria típico que os casos especiais de linhas verticais e horizontais fossem tratados separadamente, pois podem ser altamente otimizados.

Algumas versões usam os princípios de Bresenham de erro incremental de número inteiro para realizar todos os desenhos de linhas de octante, equilibrando o erro positivo e negativo entre as coordenadas xey. Observe que o pedido não é necessariamente garantido; em outras palavras, a linha pode ser traçada de (x0, y0) a (x1, y1) ou de (x1, y1) a (x0, y0).

plotLine(int x0, int y0, int x1, int y1)
    dx =  abs(x1-x0);
    sx = x0<x1 ? 1 : -1;
    dy = -abs(y1-y0);
    sy = y0<y1 ? 1 : -1;
    err = dx+dy;  /* error value e_xy */
    while (true)   /* loop */
        plot(x0, y0);
        if (x0 == x1 && y0 == y1) break;
        e2 = 2*err;
        if (e2 >= dy) /* e_xy+e_x > 0 */
            err += dy;
            x0 += sx;
        end if
        if (e2 <= dx) /* e_xy+e_y < 0 */
            err += dx;
            y0 += sy;
        end if
    end while

Algoritmos semelhantes

O algoritmo de Bresenham pode ser interpretado como um analisador diferencial digital ligeiramente modificado (usando 0,5 como limite de erro em vez de 0, que é necessário para rasterização de polígonos não sobrepostos).

O princípio de usar um erro incremental no lugar de operações de divisão tem outras aplicações em gráficos. É possível usar esta técnica para calcular as coordenadas U, V durante a varredura raster de polígonos mapeados com textura. Os motores de renderização do software voxel heightmap vistos em alguns jogos de PC também usaram esse princípio.

Bresenham também publicou um algoritmo computacional Run-Slice (em oposição ao Run-Length). Este método foi representado em várias patentes dos EUA:

Uma extensão do algoritmo que lida com linhas grossas foi criada por Alan Murphy na IBM.

Veja também

• Analisador digital diferencial (algoritmo gráfico) , um método simples e geral para rasterizar linhas e triângulos
• Algoritmo de linha de Xiaolin Wu , um método igualmente rápido de desenhar linhas com suavização
• Algoritmo de círculo de ponto médio , um algoritmo semelhante para desenhar círculos

Notas

Referências

• Bresenham, JE (1965). "Algoritmo para controle de computador de um plotter digital" (PDF) . IBM Systems Journal . 4 (1): 25–30. doi : 10.1147 / sj.41.0025 . Arquivado do original (PDF) em 28 de maio de 2008.
• "The Bresenham Line-Drawing Algorithm" , por Colin Flanagan
• Abrash, Michael (1997). Livro negro de programação gráfica de Michael Abrash . Albany, NY: Coriolis. pp.  654–678 . ISBN 978-1-57610-174-2. Uma versão muito otimizada do algoritmo em C e assembly para uso em videogames com detalhes completos de seu funcionamento interno
• Zingl, Alois (2012). "Um algoritmo de rasterização para curvas de desenho" (PDF) ., A beleza dos algoritmos de Bresenham

Leitura adicional

• A Tese de Patrick-Gilles Maillot, uma extensão do algoritmo de desenho de linhas de Bresenham para realizar a remoção de linhas ocultas 3D; também publicado nos anais do MICAD '87 sobre CAD / CAM e Computação Gráfica, página 591 - ISBN  2-86601-084-1 .
• Espessamento de linha por modificação do algoritmo de Bresenham , AS Murphy, IBM Technical Disclosure Bulletin, Vol. 20, No. 12, maio de 1978.

em vez de [qual] para uso de extensão de círculo: Relatório Técnico 1964 27 de janeiro -11- Algoritmo de Círculo TR-02-286 IBM San Jose Lab ou Um Algoritmo Linear para Exibição Digital Incremental de Arcos Circulares Fevereiro de 1977 Comunicações do ACM 20 (2 ): 100-106 DOI: 10.1145 / 359423.359432

links externos

• Edição especial do livro negro de programação gráfica de Michael Abrash: Capítulo 35: Bresenham é rápido e rápido é bom
• O Algoritmo de Desenho de Linha de Bresenham por Colin Flanagan
• Página do Instituto Nacional de Padrões e Tecnologia no algoritmo de Bresenham
• Informações do plotter incremental Calcomp 563
• Algoritmo de Bresenham em várias linguagens de programação
• The Beauty of Bresenham's Algorithm - Uma implementação simples para traçar linhas, círculos, elipses e curvas de Bézier