Força centrípeta - Centripetal force

Parte de uma série sobre
Mecânica clássica
${\displaystyle {\textbf {F}}={\frac {d}{dt}}(m{\textbf {v}})}$ Segunda lei do movimento
História Linha do tempo Livros didáticos
Galhos
Fundamentos
Formulações
Tópicos centrais
Rotação
Cientistas
Portal de física  Categoria
v t e

Uma força centrípeta (do latim centrum , "centro" e petere , "procurar") é uma força que faz um corpo seguir um caminho curvo . Sua direção é sempre ortogonal ao movimento do corpo e em direção ao ponto fixo do centro instantâneo de curvatura do caminho. Isaac Newton descreveu-o como "uma força pela qual os corpos são atraídos ou impelidos, ou de alguma forma tendem, para um ponto como para um centro". Na mecânica newtoniana , a gravidade fornece a força centrípeta que causa as órbitas astronômicas .

Um exemplo comum envolvendo força centrípeta é o caso em que um corpo se move com velocidade uniforme ao longo de um caminho circular. A força centrípeta é direcionada em ângulos retos com o movimento e também ao longo do raio em direção ao centro do caminho circular. A descrição matemática foi derivada em 1659 pelo físico holandês Christiaan Huygens .

Fórmula

A magnitude da força centrípeta em um objeto de massa m movendo-se à velocidade tangencial v ao longo de um caminho com raio de curvatura r é:

${\displaystyle F_{c}=ma_{c}={\frac {mv^{2}}{r}}}$

${\displaystyle a_{c}=\lim _{\Delta {t}\to 0}{\frac {|\Delta {\textbf {v}}|}{\Delta {t}}}}$

onde é a aceleração centrípeta e é a diferença entre os vetores de velocidade. Uma vez que os vetores de velocidade no diagrama acima têm magnitude constante e uma vez que cada um é perpendicular ao seu respectivo vetor de posição, a subtração de vetor simples implica dois triângulos isósceles semelhantes com ângulos congruentes - um compreendendo uma base de e um comprimento de perna de , e o outro um base de ( diferença de vetor de posição ) e um comprimento de perna de : ${\displaystyle a_{c}}$${\displaystyle \Delta {\textbf {v}}}$${\displaystyle \Delta {\textbf {v}}}$${\displaystyle v}$${\displaystyle \Delta {\textbf {r}}}$${\displaystyle r}$

${\displaystyle {\frac {|\Delta {\textbf {v}}|}{v}}={\frac {|\Delta {\textbf {r}}|}{r}}}$

${\displaystyle |\Delta {\textbf {v}}|={\frac {v}{r}}|\Delta {\textbf {r}}|}$

Portanto, pode ser substituído por : ${\displaystyle |\Delta {\textbf {v}}|}$${\displaystyle {\frac {v}{r}}|\Delta {\textbf {r}}|}$

${\displaystyle a_{c}=\lim _{{\Delta }t\to 0}{\frac {|\Delta {\textbf {v}}|}{\Delta {t}}}={\frac {v}{r}}\lim _{{\Delta }t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta {t}}}=\omega \lim _{{\Delta }t\to 0}{\frac {|\Delta {\textbf {r}}|}{\Delta {t}}}=v\omega ={\frac {v^{2}}{r}}}$

A direção da força é em direção ao centro do círculo em que o objeto está se movendo, ou o círculo osculante (o círculo que melhor se ajusta ao caminho local do objeto, se o caminho não for circular). A velocidade na fórmula é elevada ao quadrado, portanto, duas vezes a velocidade precisa de quatro vezes a força. A relação inversa com o raio de curvatura mostra que metade da distância radial requer o dobro da força. Esta força também é às vezes escrita em termos da velocidade angular ω do objeto sobre o centro do círculo, relacionada à velocidade tangencial pela fórmula

${\displaystyle v=\omega r}$

de modo a

${\displaystyle F_{c}=mr\omega ^{2}\,.}$

Expresso usando o período orbital T para uma revolução do círculo,

${\displaystyle \omega ={\frac {2\pi }{T}}\,}$

a equação se torna

${\displaystyle F_{c}=mr\left({\frac {2\pi }{T}}\right)^{2}.}$

Em aceleradores de partículas, a velocidade pode ser muito alta (perto da velocidade da luz no vácuo), então a mesma massa de repouso agora exerce maior inércia (massa relativística), exigindo assim maior força para a mesma aceleração centrípeta, então a equação se torna:

${\displaystyle F_{c}={\frac {\gamma mv^{2}}{r}}}$

Onde

${\displaystyle \gamma ={\frac {1}{\sqrt {1-{\frac {v^{2}}{c^{2}}}}}}}$

é o fator de Lorentz .

Assim, a força centrípeta é dada por:

${\displaystyle F_{c}=\gamma mv\omega }$

que é a taxa de variação do momento relativístico . ${\displaystyle \gamma mv}$

Fontes

Um corpo experimentando um movimento circular uniforme requer uma força centrípeta, em direção ao eixo como mostrado, para manter seu caminho circular.

No caso de um objeto que está balançando na ponta de uma corda em um plano horizontal, a força centrípeta sobre o objeto é fornecida pela tensão da corda. O exemplo da corda é um exemplo que envolve uma força de 'tração'. A força centrípeta também pode ser fornecida como uma força de 'empurrão', como no caso em que a reação normal de uma parede fornece a força centrípeta para uma parede da morte ou um cavaleiro do rotor .

A ideia de Newton de uma força centrípeta corresponde ao que hoje é referido como força central . Quando um satélite está em órbita ao redor de um planeta , a gravidade é considerada uma força centrípeta, embora no caso de órbitas excêntricas, a força gravitacional seja direcionada para o foco, e não para o centro de curvatura instantâneo.

Outro exemplo de força centrípeta surge na hélice que é traçada quando uma partícula carregada se move em um campo magnético uniforme na ausência de outras forças externas. Nesse caso, a força magnética é a força centrípeta que atua em direção ao eixo da hélice.

Análise de vários casos

Abaixo estão três exemplos de complexidade crescente, com derivações das fórmulas que regem a velocidade e a aceleração.

Movimento circular uniforme

Movimento circular uniforme refere-se ao caso de taxa de rotação constante. Aqui estão duas abordagens para descrever este caso.

Derivação de cálculo

Em duas dimensões, o vetor de posição , que tem magnitude (comprimento) e direcionado em um ângulo acima do eixo x, pode ser expresso em coordenadas cartesianas usando os vetores unitários e : ${\displaystyle {\textbf {r}}}$${\displaystyle r}$${\displaystyle \theta }$ ${\displaystyle {\hat {x}}}$${\displaystyle {\hat {y}}}$

${\displaystyle {\textbf {r}}=r\cos(\theta ){\hat {x}}+r\sin(\theta ){\hat {y}}.}$

Suponha um movimento circular uniforme , o que requer três coisas.

1. O objeto se move apenas em um círculo.
2. O raio do círculo não muda com o tempo.${\displaystyle r}$
3. O objeto se move com velocidade angular constante ao redor do círculo. Portanto, onde está o tempo.${\displaystyle \omega }$${\displaystyle \theta =\omega t}$${\displaystyle t}$

Agora encontre a velocidade e aceleração do movimento tomando as derivadas da posição em relação ao tempo. ${\displaystyle {\textbf {v}}}$ ${\displaystyle {\textbf {a}}}$

${\displaystyle {\textbf {r}}=r\cos(\omega t){\hat {x}}+r\sin(\omega t){\hat {y}}}$

${\displaystyle {\dot {\textbf {r}}}={\textbf {v}}=-r\omega \sin(\omega t){\hat {x}}+r\omega \cos(\omega t){\hat {y}}}$

${\displaystyle {\ddot {\textbf {r}}}={\textbf {a}}=-r\omega ^{2}\cos(\omega t){\hat {x}}-r\omega ^{2}\sin(\omega t){\hat {y}}}$

${\displaystyle {\textbf {a}}=-\omega ^{2}(r\cos(\omega t){\hat {x}}+r\sin(\omega t){\hat {y}})}$

Observe que o termo entre parênteses é a expressão original de em coordenadas cartesianas . Consequentemente, ${\displaystyle {\textbf {r}}}$

${\displaystyle {\textbf {a}}=-\omega ^{2}{\textbf {r}}.}$

negativo mostra que a aceleração é apontada para o centro do círculo (oposto ao raio), portanto, é chamada de "centrípeta" (ou seja, "busca do centro"). Enquanto os objetos seguem naturalmente um caminho reto (devido à inércia ), essa aceleração centrípeta descreve o caminho do movimento circular causado por uma força centrípeta.

Derivação usando vetores

Relações de vetor para movimento circular uniforme; o vetor Ω que representa a rotação é normal ao plano da órbita com polaridade determinada pela regra da mão direita e magnitude dθ / dt .

A imagem à direita mostra as relações vetoriais para movimento circular uniforme. A própria rotação é representada pelo vetor de velocidade angular Ω , que é normal ao plano da órbita (usando a regra da mão direita ) e tem magnitude dada por:

${\displaystyle |\mathbf {\Omega } |={\frac {\mathrm {d} \theta }{\mathrm {d} t}}=\omega \ ,}$

com θ a posição angular no tempo t . Nesta subseção, d θ / d t é assumido como constante, independente do tempo. A distância percorrida dℓ da partícula no tempo d t ao longo do caminho circular é

${\displaystyle \mathrm {d} {\boldsymbol {\ell }}=\mathbf {\Omega } \times \mathbf {r} (t)\mathrm {d} t\ ,}$

que, pelas propriedades do produto vetorial vetorial , tem magnitude r d θ e está na direção tangente ao caminho circular.

Consequentemente,

${\displaystyle {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}=\lim _{{\Delta }t\to 0}{\frac {\mathbf {r} (t+{\Delta }t)-\mathbf {r} (t)}{{\Delta }t}}={\frac {\mathrm {d} {\boldsymbol {\ell }}}{\mathrm {d} t}}\ .}$

Em outras palavras,

${\displaystyle \mathbf {v} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}={\frac {\mathrm {d} \mathbf {\boldsymbol {\ell }} }{\mathrm {d} t}}=\mathbf {\Omega } \times \mathbf {r} (t)\ .}$

Diferenciando com relação ao tempo,

${\displaystyle \mathbf {a} \ {\stackrel {\mathrm {def} }{=}}\ {\frac {\mathrm {d} \mathbf {v} }{d\mathrm {t} }}=\mathbf {\Omega } \times {\frac {\mathrm {d} \mathbf {r} (t)}{\mathrm {d} t}}=\mathbf {\Omega } \times \left[\mathbf {\Omega } \times \mathbf {r} (t)\right]\ .}$

A fórmula de Lagrange afirma:

${\displaystyle \mathbf {a} \times \left(\mathbf {b} \times \mathbf {c} \right)=\mathbf {b} \left(\mathbf {a} \cdot \mathbf {c} \right)-\mathbf {c} \left(\mathbf {a} \cdot \mathbf {b} \right)\ .}$

Aplicando a fórmula de Lagrange com a observação de que Ω • r ( t ) = 0 em todos os momentos,

${\displaystyle \mathbf {a} =-{|\mathbf {\Omega |} }^{2}\mathbf {r} (t)\ .}$

Em palavras, a aceleração está apontando diretamente para o lado oposto ao deslocamento radial r em todos os momentos e tem uma magnitude:

${\displaystyle |\mathbf {a} |=|\mathbf {r} (t)|\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}=r{\omega }^{2}\ }$

onde barras verticais | ... | denotam a magnitude do vetor, que no caso de r ( t ) é simplesmente o raio r do caminho. Este resultado concorda com a seção anterior, embora a notação seja um pouco diferente.

Quando a taxa de rotação é tornada constante na análise do movimento circular não uniforme , essa análise concorda com esta.

Um mérito da abordagem vetorial é que ela é manifestamente independente de qualquer sistema de coordenadas.

Exemplo: a curva inclinada

Painel superior: bola em uma pista circular inclinada movendo-se com velocidade constante v ; Painel inferior: Forças na bola

O painel superior na imagem à direita mostra uma bola em movimento circular em uma curva inclinada. A curva é inclinada em um ângulo θ em relação à horizontal e a superfície da estrada é considerada escorregadia. O objetivo é saber qual o ângulo que a inclinação deve ter para que a bola não deslize para fora da estrada. A intuição nos diz que, em uma curva plana sem nenhuma inclinação, a bola simplesmente deslizará para fora da estrada; enquanto com uma inclinação muito acentuada, a bola deslizará para o centro, a menos que faça a curva rapidamente.

Além de qualquer aceleração que possa ocorrer na direção do caminho, o painel inferior da imagem acima indica as forças na bola. Existem duas forças; um é a força da gravidade verticalmente para baixo através do centro de massa da bola m g , onde m é a massa da bola eg é a aceleração gravitacional ; a segunda é a força normal para cima exercida pela estrada em um ângulo reto com a superfície da estrada m a _n . A força centrípeta exigida pelo movimento curvo também é mostrada acima. Essa força centrípeta não é uma terceira força aplicada à bola, mas deve ser fornecida pela força resultante na bola, resultante da adição vetorial da força normal e da força da gravidade . A força resultante ou resultante na bola encontrada pela adição vetorial da força normal exercida pela estrada e a força vertical devido à gravidade deve ser igual à força centrípeta ditada pela necessidade de percorrer um caminho circular. O movimento curvo é mantido enquanto essa força resultante fornecer a força centrípeta necessária ao movimento.

A força resultante horizontal na bola é o componente horizontal da força vinda da estrada, que tem magnitude | F _h | = m | a _n | sin θ . A componente vertical da força proveniente da estrada deve neutralizar a força gravitacional: | F _v | = m | a _n | cos θ = m | g |, o que implica | a _n | = | g | / cos θ . Substituindo na fórmula acima para | F _h | produz uma força horizontal para ser:

${\displaystyle |\mathbf {F} _{\mathrm {h} }|=m|\mathbf {g} |{\frac {\mathrm {sin} \ \theta }{\mathrm {cos} \ \theta }}=m|\mathbf {g} |\mathrm {tan} \ \theta \ .}$

Por outro lado, em velocidade | v | em um caminho circular de raio r , a cinemática diz que a força necessária para girar a bola continuamente na curva é a força centrípeta radialmente para dentro F _c de magnitude:

${\displaystyle |\mathbf {F} _{\mathrm {c} }|=m|\mathbf {a} _{\mathrm {c} }|={\frac {m|\mathbf {v} |^{2}}{r}}\ .}$

Consequentemente, a bola está em um caminho estável quando o ângulo da estrada é definido para satisfazer a condição:

${\displaystyle m|\mathbf {g} |\mathrm {tan} \ \theta ={\frac {m|\mathbf {v} |^{2}}{r}}\ ,}$

ou,

${\displaystyle \mathrm {tan} \ \theta ={\frac {|\mathbf {v} |^{2}}{|\mathbf {g} |r}}\ .}$

Conforme o ângulo do banco θ se aproxima de 90 °, a função tangente se aproxima do infinito, permitindo valores maiores para | v | ² / r . Em palavras, esta equação afirma que para velocidades maiores (maior | v |) a estrada deve ser inclinada mais abruptamente (um valor maior para θ ), e para curvas mais fechadas ( r menor ) a estrada também deve ser inclinada mais abruptamente, o que está de acordo com intuição. Quando o ângulo θ não satisfaz a condição acima, o componente horizontal da força exercida pela estrada não fornece a força centrípeta correta e uma força de atrito tangencial adicional à superfície da estrada é chamada para fornecer a diferença. Se o atrito não puder fazer isso (ou seja, o coeficiente de atrito é excedido), a bola desliza para um raio diferente onde o equilíbrio pode ser realizado.

Essas idéias também se aplicam a voos aéreos. Consulte o manual do piloto da FAA.

Movimento circular não uniforme

Velocidade e aceleração para movimento circular não uniforme: o vetor velocidade é tangencial à órbita, mas o vetor aceleração não é radialmente para dentro por causa de sua componente tangencial a _θ que aumenta a taxa de rotação: d ω / dt = | a _θ | / R .

Como uma generalização do caso do movimento circular uniforme, suponha que a taxa angular de rotação não seja constante. A aceleração agora tem um componente tangencial, conforme mostra a imagem à direita. Este caso é usado para demonstrar uma estratégia de derivação baseada em um sistema de coordenadas polares .

Seja r ( t ) um vetor que descreve a posição de uma massa pontual em função do tempo. Como estamos assumindo um movimento circular , seja r ( t ) = R · u _r , onde R é uma constante (o raio do círculo) e u _r é o vetor unitário que aponta da origem para a massa do ponto. A direção de u _r é descrita por θ , o ângulo entre o eixo x e o vetor unitário, medido no sentido anti-horário a partir do eixo x. O outro vetor unitário para coordenadas polares, u _θ é perpendicular a u _r e aponta na direção de aumento de θ . Estes vectores unitários polares pode ser expressa em termos de cartesianas vectores de unidade nas x e y instruções, denotado i e j , respectivamente:

u _r = cos θ i + sin θ j

e

u _θ = -sin θ i + cos θ j .

Pode-se diferenciar para encontrar velocidade:

${\displaystyle \mathbf {v} =r{\frac {\mathrm {d} \mathbf {u} _{\mathrm {r} }}{\mathrm {d} t}}=r{\frac {\mathrm {d} }{\mathrm {d} t}}\left(\mathrm {cos} \ \theta \ \mathbf {i} +\mathrm {sin} \ \theta \ \mathbf {j} \right)}$

${\displaystyle =r{\frac {d\theta }{dt}}\left(-\mathrm {sin} \ \theta \ \mathbf {i} +\mathrm {cos} \ \theta \ \mathbf {j} \right)\,}$

${\displaystyle =r{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {u} _{\mathrm {\theta } }\,}$

${\displaystyle =\omega r\mathbf {u} _{\mathrm {\theta } }\,}$

onde ω é a velocidade angular d θ / d t .

Este resultado para a velocidade corresponde às expectativas de que a velocidade deve ser direcionada tangencialmente ao círculo e que a magnitude da velocidade deve ser rω . Diferenciando novamente, e observando que

${\displaystyle {{\frac {\mathrm {d} \mathbf {u} _{\mathrm {\theta } }}{\mathrm {d} t}}=-{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {u} _{\mathrm {r} }=-\omega \mathbf {u} _{\mathrm {r} }}\ ,}$

descobrimos que a aceleração, a é:

${\displaystyle \mathbf {a} =r\left({\frac {\mathrm {d} \omega }{\mathrm {d} t}}\mathbf {u} _{\mathrm {\theta } }-\omega ^{2}\mathbf {u} _{\mathrm {r} }\right)\ .}$

Assim, os componentes radial e tangencial da aceleração são:

${\displaystyle \mathbf {a} _{\mathrm {r} }=-\omega ^{2}r\ \mathbf {u} _{\mathrm {r} }=-{\frac {|\mathbf {v} |^{2}}{r}}\ \mathbf {u} _{\mathrm {r} }\ }$   e   ${\displaystyle \ \mathbf {a} _{\mathrm {\theta } }=r\ {\frac {\mathrm {d} \omega }{\mathrm {d} t}}\ \mathbf {u} _{\mathrm {\theta } }={\frac {\mathrm {d} |\mathbf {v} |}{\mathrm {d} t}}\ \mathbf {u} _{\mathrm {\theta } }\ ,}$

onde | v | = r ω é a magnitude da velocidade (a velocidade).

Essas equações expressam matematicamente que, no caso de um objeto que se move ao longo de um caminho circular com uma velocidade variável, a aceleração do corpo pode ser decomposta em um componente perpendicular que muda a direção do movimento (a aceleração centrípeta), e um paralelo , ou componente tangencial , que altera a velocidade.

Movimento plano geral

Vetor de posição r , sempre aponta radialmente a partir da origem.

Vetor velocidade v , sempre tangente à trajetória do movimento.

Vetor de aceleração a , não paralelo ao movimento radial, mas desviado pelas acelerações angular e de Coriolis, nem tangente ao caminho, mas desviado pelas acelerações centrípeta e radial.

Vetores cinemáticos em coordenadas polares planas. Observe que a configuração não está restrita ao espaço 2D, mas a um plano em qualquer dimensão superior.

Vetores unitários polares em dois tempos t e t + dt para uma partícula com trajetória r ( t ); à esquerda, os vetores unitários u _ρ e u _θ nos dois tempos são movidos de forma que suas caudas se encontrem, e são mostrados traçando um arco de um círculo de raio unitário. Sua rotação no tempo dt é d θ, exatamente o mesmo ângulo da rotação da trajetória r ( t ).

Coordenadas polares

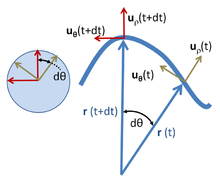
Os resultados acima podem ser derivados talvez mais simplesmente em coordenadas polares e, ao mesmo tempo, estendidos para o movimento geral dentro de um plano, como mostrado a seguir. As coordenadas polares no plano empregam um vetor unitário radial u _ρ e um vetor unitário angular u _θ , como mostrado acima. Uma partícula na posição r é descrita por:

${\displaystyle \mathbf {r} =\rho \mathbf {u} _{\rho }\ ,}$

onde a notação ρ é usada para descrever a distância do caminho desde a origem em vez de R para enfatizar que essa distância não é fixa, mas varia com o tempo. O vetor unitário u _ρ viaja com a partícula e sempre aponta na mesma direção que r ( t ). O vetor unitário u _θ também viaja com a partícula e permanece ortogonal a u _ρ . Assim, u _ρ e u _θ formam um sistema de coordenadas cartesianas local anexado à partícula, e amarrado ao caminho percorrido pela partícula. Ao mover os vetores unitários para que suas caudas coincidam, como visto no círculo à esquerda da imagem acima, é visto que u _ρ e u _θ formam um par em ângulo reto com pontas no círculo unitário que traçam para frente e para trás o perímetro deste círculo com o mesmo ângulo θ ( t ) que r ( t ).

Quando a partícula se move, sua velocidade é

${\displaystyle \mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho {\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}\ .}$

Para avaliar a velocidade, a derivada do vetor unitário u _ρ é necessária. Como u _ρ é um vetor unitário, sua magnitude é fixa e só pode mudar na direção, ou seja, sua mudança d u _ρ tem uma componente apenas perpendicular a u _ρ . Quando a trajetória r ( t ) gira em um valor d θ , u _ρ , que aponta na mesma direção de r ( t ), também gira em d θ . Veja a imagem acima. Portanto, a mudança em u _ρ é

${\displaystyle \mathrm {d} \mathbf {u} _{\rho }=\mathbf {u} _{\theta }\mathrm {d} \theta \ ,}$

ou

${\displaystyle {\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}=\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\ .}$

De maneira semelhante, a taxa de variação de u _θ é encontrada. Como com u _ρ , u _θ é um vetor unitário e só pode girar sem alterar o tamanho. Para permanecer ortogonal a u _ρ enquanto a trajetória r ( t ) gira uma quantidade d θ , u _θ , que é ortogonal a r ( t ), também gira por d θ . Veja a imagem acima. Portanto, a mudança d u _θ é ortogonal a u _θ e proporcional a d θ (ver imagem acima):

${\displaystyle {\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}=-{\frac {\mathrm {d} \theta }{\mathrm {d} t}}\mathbf {u} _{\rho }\ .}$

A imagem acima mostra que o sinal é negativo: para manter a ortogonalidade, se d u _ρ for positivo com d θ , então d u _θ deve diminuir.

Substituindo a derivada de u _ρ na expressão de velocidade:

${\displaystyle \mathbf {v} ={\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\rho }+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}=v_{\rho }\mathbf {u} _{\rho }+v_{\theta }\mathbf {u} _{\theta }=\mathbf {v} _{\rho }+\mathbf {v} _{\theta }\ .}$

Para obter a aceleração, outra diferenciação de tempo é feita:

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \mathbf {u} _{\rho }}{\mathrm {d} t}}+{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} \mathbf {u} _{\theta }}{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\ .}$

Substituindo as derivadas de u _ρ e u _θ , a aceleração da partícula é:

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}\mathbf {u} _{\rho }+2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}\mathbf {u} _{\theta }{\frac {\mathrm {d} \theta }{\mathrm {d} t}}-\rho \mathbf {u} _{\rho }\left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}+\rho \mathbf {u} _{\theta }{\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\ ,}$

${\displaystyle =\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} ^{2}\rho }{\mathrm {d} t^{2}}}-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[2{\frac {\mathrm {d} \rho }{\mathrm {d} t}}{\frac {\mathrm {d} \theta }{\mathrm {d} t}}+\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]\ }$

${\displaystyle =\mathbf {u} _{\rho }\left[{\frac {\mathrm {d} v_{\rho }}{\mathrm {d} t}}-{\frac {v_{\theta }^{2}}{\rho }}\right]+\mathbf {u} _{\theta }\left[{\frac {2}{\rho }}v_{\rho }v_{\theta }+\rho {\frac {\mathrm {d} }{\mathrm {d} t}}{\frac {v_{\theta }}{\rho }}\right]\ .}$

Como um exemplo particular, se a partícula se move em um círculo de raio constante R , então d ρ / d t = 0, v = v _θ , e:

${\displaystyle \mathbf {a} =\mathbf {u} _{\rho }\left[-\rho \left({\frac {\mathrm {d} \theta }{\mathrm {d} t}}\right)^{2}\right]+\mathbf {u} _{\theta }\left[\rho {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}\right]\ }$

${\displaystyle =\mathbf {u} _{\rho }\left[-{\frac {v^{2}}{r}}\right]+\mathbf {u} _{\theta }\left[{\frac {\mathrm {d} v}{\mathrm {d} t}}\right]\ }$

Onde ${\displaystyle v=v_{\theta }.}$

Esses resultados concordam com aqueles acima para movimentos circulares não uniformes . Veja também o artigo sobre movimento circular não uniforme . Se essa aceleração for multiplicada pela massa da partícula, o termo principal é a força centrípeta e o negativo do segundo termo relacionado à aceleração angular é algumas vezes chamado de força de Euler .

Para trajetórias diferentes do movimento circular, por exemplo, a trajetória mais geral prevista na imagem acima, o centro de rotação instantâneo e o raio de curvatura da trajetória estão relacionados apenas indiretamente ao sistema de coordenadas definido por u _ρ e u _θ e ao comprimento | r ( t ) | = ρ . Consequentemente, no caso geral, não é fácil separar os termos centrípetos e de Euler da equação de aceleração geral acima. Para lidar diretamente com este problema, as coordenadas locais são preferíveis, como discutido a seguir.

Coordenadas locais

Sistema de coordenadas local para movimento plano em uma curva. Duas posições diferentes são mostradas para distâncias s e s + ds ao longo da curva. Em cada posição s , o vetor unitário u _n aponta ao longo da normal externa à curva e o vetor unitário u _t é tangencial ao caminho. O raio de curvatura da trajetória é ρ conforme encontrado a partir da taxa de rotação da tangente à curva em relação ao comprimento do arco, e é o raio do círculo osculante na posição s . O círculo unitário à esquerda mostra a rotação dos vetores unitários com s .

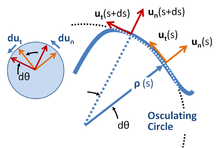
Coordenadas locais significam um conjunto de coordenadas que viajam com a partícula e têm orientação determinada pelo caminho da partícula. Os vetores unitários são formados conforme mostrado na imagem à direita, tangenciais e normais ao caminho. Este sistema de coordenadas, por vezes é referido como intrínsecos ou coordenadas de caminho ou nt-coordenadas , para normal tangencial , referindo-se estes vectores unitários. Essas coordenadas são um exemplo muito especial de um conceito mais geral de coordenadas locais da teoria das formas diferenciais.

A distância ao longo do caminho da partícula é o comprimento do arco s , considerado uma função conhecida do tempo.

${\displaystyle s=s(t)\ .}$

Um centro de curvatura é definido em cada posição s localizada a uma distância ρ (o raio de curvatura ) da curva em uma linha ao longo de u _n ( s ) normal . A distância necessária ρ ( s ) no comprimento do arco s é definida em termos da taxa de rotação da tangente à curva, que por sua vez é determinada pelo próprio caminho. Se a orientação da tangente em relação a alguma posição inicial é θ ( s ), então ρ ( s ) é definido pela derivada d θ / d s :

${\displaystyle {\frac {1}{\rho (s)}}=\kappa (s)={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .}$

O raio de curvatura geralmente é considerado positivo (isto é, como um valor absoluto), enquanto a curvatura κ é uma quantidade sinalizada.

Uma abordagem geométrica para encontrar o centro de curvatura e o raio de curvatura usa um processo de limitação que leva ao círculo osculante . Veja a imagem acima.

Usando essas coordenadas, o movimento ao longo do caminho é visto como uma sucessão de caminhos circulares de centro em constante mudança, e em cada posição s constitui um movimento circular não uniforme naquela posição com raio ρ . O valor local da taxa angular de rotação, então, é dado por:

${\displaystyle \omega (s)={\frac {\mathrm {d} \theta }{\mathrm {d} t}}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}{\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {1}{\rho (s)}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {v(s)}{\rho (s)}}\ ,}$

com a velocidade local v dada por:

${\displaystyle v(s)={\frac {\mathrm {d} s}{\mathrm {d} t}}\ .}$

Quanto aos outros exemplos acima, porque os vetores unitários não podem mudar de magnitude, sua taxa de mudança é sempre perpendicular à sua direção (veja a inserção do lado esquerdo na imagem acima):

${\displaystyle {\frac {d\mathbf {u} _{\mathrm {n} }(s)}{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {d\theta }{ds}}=\mathbf {u} _{\mathrm {t} }(s){\frac {1}{\rho }}\ ;}$ ${\displaystyle {\frac {d\mathbf {u} _{\mathrm {t} }(s)}{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} \theta }{\mathrm {d} s}}=-\mathbf {u} _{\mathrm {n} }(s){\frac {1}{\rho }}\ .}$

Consequentemente, a velocidade e a aceleração são:

${\displaystyle \mathbf {v} (t)=v\mathbf {u} _{\mathrm {t} }(s)\ ;}$

e usando a regra da cadeia de diferenciação :

${\displaystyle \mathbf {a} (t)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\ ;}$ com a aceleração tangencial ${\displaystyle {\frac {\mathrm {\mathrm {d} } v}{\mathrm {\mathrm {d} } t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ {\frac {\mathrm {d} s}{\mathrm {d} t}}={\frac {\mathrm {d} v}{\mathrm {d} s}}\ v\ .}$

Neste sistema de coordenadas local, a aceleração se assemelha à expressão para movimento circular não uniforme com o raio local ρ ( s ), e a aceleração centrípeta é identificada como o segundo termo.

O alargamento desta abordagem às curvas do espaço tridimensional conduz às fórmulas de Frenet – Serret .

Abordagem alternativa

Olhando para a imagem acima, pode-se perguntar se a consideração adequada foi levada em consideração a diferença na curvatura entre ρ ( s ) e ρ ( s + d s ) no cálculo do comprimento do arco como d s = ρ ( s ) d θ . A garantia sobre este ponto pode ser encontrada usando uma abordagem mais formal descrita abaixo. Esta abordagem também faz conexão com o artigo sobre curvatura .

Para introduzir os vetores unitários do sistema de coordenadas local, uma abordagem é começar nas coordenadas cartesianas e descrever as coordenadas locais em termos dessas coordenadas cartesianas. Em termos de comprimento de arco s , deixe o caminho ser descrito como:

${\displaystyle \mathbf {r} (s)=\left[x(s),\ y(s)\right]\ .}$

Então, um deslocamento incremental ao longo do caminho d s é descrito por:

${\displaystyle \mathrm {d} \mathbf {r} (s)=\left[\mathrm {d} x(s),\ \mathrm {d} y(s)\right]=\left[x'(s),\ y'(s)\right]\mathrm {d} s\ ,}$

onde os primos são introduzidos para denotar derivados em relação a s . A magnitude desse deslocamento é d s , mostrando que:

${\displaystyle \left[x'(s)^{2}+y'(s)^{2}\right]=1\ .}$ (Eq. 1)

Este deslocamento é necessariamente uma tangente à curva em s , mostrando que o vetor unitário tangente à curva é:

${\displaystyle \mathbf {u} _{\mathrm {t} }(s)=\left[x'(s),\ y'(s)\right]\ ,}$

enquanto o vetor unitário externo normal à curva é

${\displaystyle \mathbf {u} _{\mathrm {n} }(s)=\left[y'(s),\ -x'(s)\right]\ ,}$

A ortogonalidade pode ser verificada mostrando que o produto escalar do vetor é zero. A magnitude da unidade desses vetores é uma consequência da Eq. 1 . Usando o vetor tangente, o ângulo θ da tangente à curva é dado por:

${\displaystyle \sin \theta ={\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=y'(s)\ ;}$ e ${\displaystyle \cos \theta ={\frac {x'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}=x'(s)\ .}$

O raio de curvatura é introduzido de forma completamente formal (sem necessidade de interpretação geométrica) como:

${\displaystyle {\frac {1}{\rho }}={\frac {\mathrm {d} \theta }{\mathrm {d} s}}\ .}$

A derivada de θ pode ser encontrada para sin θ :

${\displaystyle {\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}=\cos \theta {\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}\cos \theta \ ={\frac {1}{\rho }}x'(s)\ .}$

Agora:

${\displaystyle {\frac {\mathrm {d} \sin \theta }{\mathrm {d} s}}={\frac {\mathrm {d} }{\mathrm {d} s}}{\frac {y'(s)}{\sqrt {x'(s)^{2}+y'(s)^{2}}}}}$ ${\displaystyle ={\frac {y''(s)x'(s)^{2}-y'(s)x'(s)x''(s)}{\left(x'(s)^{2}+y'(s)^{2}\right)^{3/2}}}\ ,}$

em que o denominador é a unidade. Com esta fórmula para a derivada do seno, o raio de curvatura torna-se:

${\displaystyle {\frac {\mathrm {d} \theta }{\mathrm {d} s}}={\frac {1}{\rho }}=y''(s)x'(s)-y'(s)x''(s)\ }$ ${\displaystyle ={\frac {y''(s)}{x'(s)}}=-{\frac {x''(s)}{y'(s)}}\ ,}$

onde a equivalência das formas deriva da diferenciação da Eq. 1 :

${\displaystyle x'(s)x''(s)+y'(s)y''(s)=0\ .}$

Com esses resultados, a aceleração pode ser encontrada:

${\displaystyle \mathbf {a} (s)={\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {v} (s)}$ ${\displaystyle ={\frac {\mathrm {d} }{\mathrm {d} t}}\left[{\frac {\mathrm {d} s}{\mathrm {d} t}}\left(x'(s),\ y'(s)\right)\right]\ }$

${\displaystyle =\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)+\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}\left(x''(s),\ y''(s)\right)}$

${\displaystyle =\left({\frac {\mathrm {d} ^{2}s}{\mathrm {d} t^{2}}}\right)\mathbf {u} _{\mathrm {t} }(s)-\left({\frac {\mathrm {d} s}{\mathrm {d} t}}\right)^{2}{\frac {1}{\rho }}\mathbf {u} _{\mathrm {n} }(s)\ ,}$

como pode ser verificado tomando o produto escalar com os vetores unitários u _t ( s ) e u _n ( s ). Este resultado para a aceleração é igual ao do movimento circular baseado no raio ρ . Usando este sistema de coordenadas no referencial inercial, é fácil identificar a força normal à trajetória como a força centrípeta e aquela paralela à trajetória como a força tangencial. Do ponto de vista qualitativo, o caminho pode ser aproximado por um arco de círculo por um tempo limitado, e por um tempo limitado se aplica um raio de curvatura particular, as forças centrífugas e de Euler podem ser analisadas com base no movimento circular com esse raio .

Este resultado para aceleração está de acordo com o encontrado anteriormente. No entanto, nesta abordagem, a questão da mudança no raio de curvatura com s é tratada de forma completamente formal, consistente com uma interpretação geométrica, mas não contando com ela, evitando assim quaisquer questões que a imagem acima possa sugerir sobre negligenciar a variação em ρ .

Exemplo: movimento circular

Para ilustrar as fórmulas acima, sejam x , y dados como:

${\displaystyle x=\alpha \cos {\frac {s}{\alpha }}\ ;\ y=\alpha \sin {\frac {s}{\alpha }}\ .}$

Então:

${\displaystyle x^{2}+y^{2}=\alpha ^{2}\ ,}$

que pode ser reconhecido como um caminho circular em torno da origem com raio α . A posição s = 0 corresponde a [ α , 0] ou 3 horas. Para usar o formalismo acima, os derivados são necessários:

${\displaystyle y^{\prime }(s)=\cos {\frac {s}{\alpha }}\ ;\ x^{\prime }(s)=-\sin {\frac {s}{\alpha }}\ ,}$

${\displaystyle y^{\prime \prime }(s)=-{\frac {1}{\alpha }}\sin {\frac {s}{\alpha }}\ ;\ x^{\prime \prime }(s)=-{\frac {1}{\alpha }}\cos {\frac {s}{\alpha }}\ .}$

Com esses resultados, pode-se verificar que:

${\displaystyle x^{\prime }(s)^{2}+y^{\prime }(s)^{2}=1\ ;\ {\frac {1}{\rho }}=y^{\prime \prime }(s)x^{\prime }(s)-y^{\prime }(s)x^{\prime \prime }(s)={\frac {1}{\alpha }}\ .}$

Os vetores unitários também podem ser encontrados:

${\displaystyle \mathbf {u} _{\mathrm {t} }(s)=\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]\ ;\ \mathbf {u} _{\mathrm {n} }(s)=\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]\ ,}$

que servem para mostrar que s = 0 está localizado na posição [ ρ , 0] e s = ρ π / 2 em [0, ρ ], o que concorda com as expressões originais para x e y . Em outras palavras, s é medido no sentido anti-horário em torno do círculo a partir das 3 horas. Além disso, os derivados desses vetores podem ser encontrados:

${\displaystyle {\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {t} }(s)=-{\frac {1}{\alpha }}\left[\cos {\frac {s}{\alpha }}\ ,\ \sin {\frac {s}{\alpha }}\right]=-{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ;}$

${\displaystyle \ {\frac {\mathrm {d} }{\mathrm {d} s}}\mathbf {u} _{\mathrm {n} }(s)={\frac {1}{\alpha }}\left[-\sin {\frac {s}{\alpha }}\ ,\ \cos {\frac {s}{\alpha }}\right]={\frac {1}{\alpha }}\mathbf {u} _{\mathrm {t} }(s)\ .}$

Para obter velocidade e aceleração, uma dependência do tempo para s é necessária. Para movimento anti-horário em velocidade variável v ( t ):

${\displaystyle s(t)=\int _{0}^{t}\ dt^{\prime }\ v(t^{\prime })\ ,}$

onde v ( t ) é a velocidade e t é o tempo e s ( t = 0) = 0. Então:

${\displaystyle \mathbf {v} =v(t)\mathbf {u} _{\mathrm {t} }(s)\ ,}$

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)+v{\frac {\mathrm {d} }{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-v{\frac {1}{\alpha }}\mathbf {u} _{\mathrm {n} }(s){\frac {\mathrm {d} s}{\mathrm {d} t}}}$

${\displaystyle \mathbf {a} ={\frac {\mathrm {d} v}{\mathrm {d} t}}\mathbf {u} _{\mathrm {t} }(s)-{\frac {v^{2}}{\alpha }}\mathbf {u} _{\mathrm {n} }(s)\ ,}$

onde já está estabelecido que α = ρ. Esta aceleração é o resultado padrão para movimentos circulares não uniformes .

Veja também

Notas e referências

Leitura adicional

• Serway, Raymond A .; Jewett, John W. (2004). Physics for Scientists and Engineers (6ª ed.). Brooks / Cole. ISBN 978-0-534-40842-8.
• Tipler, Paul (2004). Física para Cientistas e Engenheiros: Mecânica, Oscilações e Ondas, Termodinâmica (5ª ed.). WH Freeman. ISBN 978-0-7167-0809-4.
• Força centrípeta vs. força centrífuga , de um tutorial online de física do Exame de Regentes pelo distrito escolar de Oswego City

links externos

• Notas da Universidade de Winnipeg
• Notas de Física e Astronomia Hiperfísica na Georgia State University ; veja também a página inicial
• Notas da Britannica
• Notas da PhysicsNet
• Notas da NASA por David P. Stern
• Notas de U Texas .
• Análise de ioiô inteligente
• O iô-iô Inuit
• Kinematic Models for Design Digital Library (KMODDL)
  Filmes e fotos de centenas de modelos de sistemas mecânicos em funcionamento na Cornell University. Também inclui uma biblioteca de livros eletrônicos com textos clássicos sobre design mecânico e engenharia.