4 politopo regular - Regular 4-polytope

O tesserato é um dos 6 politopos regulares convexos de 4

Em matemática , um regulares 4-polytope é um regulares polytope quatro dimensões . Eles são os análogos quadridimensionais dos poliedros regulares em três dimensões e dos polígonos regulares em duas dimensões.

Existem seis 4 politopos regulares convexos e dez estrelas regulares, dando um total de dezesseis.

História

Os 4 politopos regulares convexos foram descritos pela primeira vez pelo matemático suíço Ludwig Schläfli em meados do século XIX. Ele descobriu que existem exatamente seis dessas figuras.

Schläfli também encontrou quatro das estrelas regulares de 4 politopos: a grande 120 células , a grande estrelada de 120 células , a grande 600 células e a grande estrela de 120 células . Ele pulou os seis restantes porque não permitiria formas que falhassem na característica de Euler em células ou figuras de vértice (para toros de orifício zero: F  -  E  +  V  = 2). Isso exclui células e figuras de vértice, como o grande dodecaedro {5,5/2} e pequeno dodecaedro estrelado {5/2, 5}.

Edmund Hess (1843–1903) publicou a lista completa em seu livro alemão de 1883 Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder .

Construção

A existência de um 4-politopo regular é restringida pela existência de poliedros regulares que formam suas células e uma restrição de ângulo diedro${\ displaystyle \ {p, q, r \}}$${\ displaystyle \ {p, q \}, \ {q, r \}}$

${\ displaystyle \ sin {\ frac {\ pi} {p}} \ sin {\ frac {\ pi} {r}} <\ cos {\ frac {\ pi} {q}}}$

para garantir que as células se encontram para formar uma superfície 3 fechada.

Os seis politopos convexos e dez estrelas descritos são as únicas soluções para essas restrições.

Existem quatro símbolos Schläfli não convexos {p, q, r} que têm células válidas {p, q} e figuras de vértice {q, r} e passam no teste diédrico, mas não conseguem produzir figuras finitas: {3,5/2, 3}, {4,3,5/2}, { 5/2, 3,4}, { 5/2, 3,5/2}

4 politopos convexos regulares

Os 4 politopos convexos regulares são os análogos quadridimensionais dos sólidos platônicos em três dimensões e os polígonos regulares convexos em duas dimensões.

Cinco dos seis são claramente análogos dos cinco sólidos platônicos correspondentes. O sexto, o de 24 células , não tem um análogo regular em três dimensões. No entanto, existe um par de sólidos irregulares, o cuboctaedro e seu dual, o dodecaedro rômbico , que são análogos parciais ao de 24 células (em formas complementares). Juntos, eles podem ser vistos como o análogo tridimensional das 24 células.

Cada politopo 4 regular convexo é delimitado por um conjunto de células tridimensionais que são todos sólidos platônicos do mesmo tipo e tamanho. Eles são encaixados ao longo de suas respectivas faces de maneira regular.

Propriedades

Como seus análogos tridimensionais, os 4 politopos regulares convexos podem ser naturalmente ordenados por tamanho como uma medida do conteúdo 4-dimensional (hipervolume) para o mesmo raio. Cada politopo maior na sequência é mais redondo que seu predecessor, envolvendo mais conteúdo no mesmo raio. O 4-simplex (5 células) é o menor caso limite e o 120 células é o maior. A complexidade (medida pela comparação de matrizes de configuração ou simplesmente o número de vértices) segue a mesma ordem.

4 politopos convexos regulares
Grupo de simetria	A 4	B 4		F 4	H 4
Nome	5 células hiper tetraedro	16 células hiper octaedro	8 células hiper cubo	24 células	600 células hiper icosaedro	120 células hiper dodecaedro
Símbolo Schläfli	{3, 3, 3}	{3, 3, 4}	{4, 3, 3}	{3, 4, 3}	{3, 3, 5}	{5, 3, 3}
Diagrama de Coxeter
Gráfico
Vértices	5	8	16	24	120	600
Arestas	10	24	32	96	720	1200
Rostos	10 triângulos	32 triângulos	24 quadrados	96 triângulos	1200 triângulos	720 pentágonos
Células	5 tetraedros	16 tetraedros	8 cubos	24 octaedros	600 tetraedros	120 dodecaedros
Raio longo	1	1	1	1	1	1
Comprimento da aresta	√ 5/√ 2 ≈ 1.581	√ 2 ≈ 1,414	1	1	1/ϕ ≈ 0,618	1/√ 2 ϕ 2 ≈ 0,270
Raio curto	1/4	1/2	1/2	√ 2/2 ≈ 0,707	1 - (√ 2/2 √ 3 φ) 2 ≈ 0,936	1 - (1/2 √ 3 φ) 2 ≈ 0,968
Área	10 •√ 8/3 ≈ 9.428	32 •√ 3/4 ≈ 13.856	24	96 •√ 3/4 ≈ 41.569	1200 •√ 3/8φ 2 ≈ 99.238	720 •25 + 10 √ 5/8φ 4 ≈ 621,9
Volume	5 •5 √ 5/24 ≈ 2.329	16 •1/3 ≈ 5,333	8	24 •√ 2/3 ≈ 11.314	600 •1/3 √ 8 φ 3 ≈ 16.693	120 •2 + φ/2 √ 8 φ 3 ≈ 18,118
4-Conteúdo	√ 5/24• (√ 5/2) 4 ≈ 0,146	2/3 ≈ 0,667	1	2	Curto ∙ Vol/4 ≈ 3.907	Curto ∙ Vol/4 ≈ 4.385

A tabela a seguir lista algumas propriedades dos seis 4 politopos regulares convexos. Os grupos de simetria desses 4 politopos são todos grupos de Coxeter e fornecidos na notação descrita naquele artigo. O número após o nome do grupo é a ordem do grupo.

Nomes	Imagem	Família	Schläfli Coxeter	V	E	F	C	Vert. FIG.	Dual	Grupo de simetria
Pentachoron pentatope 4-simplex de 5 células		n- simples (famíliaA n )	{3,3,3}	5	10	10 {3}	5 {3,3}	{3,3}	autoduplicado	A 4 [3,3,3]	120
Hexadecachoron 4-orthoplex de 16 células		n- ortoplexo (famíliaB n )	{3,3,4}	8	24	32 {3}	16 {3,3}	{3,4}	8 células	B 4 [4,3,3]	384
8-cell octachoron tesseract 4-cube		hipercubo n- cubo ( família B n )	{4,3,3}	16	32	24 {4}	8 {4,3}	{3,3}	16 células
Icositetrachoron octaplex polioctaedro (pO) de 24 células		F n família	{3,4,3}	24	96	96 {3}	24 {3,4}	{4,3}	autoduplicado	F 4 [3,4,3]	1152
Hexacosichoron tetraplex politetraedro de 600 células (pT)		politopo n-pentagonal ( família H n )	{3,3,5}	120	720	1200 {3}	600 {3,3}	{3,5}	120 células	H 4 [5,3,3]	14400
Hecatonicosachoron dodecacontachoron dodecaedro polidodecaedro ( pD ) de 120 células		politopo n-pentagonal ( família H n )	{5,3,3}	600	1200	720 {5}	120 {5,3}	{3,3}	600 células

John Conway defendeu os nomes simplex, orthoplex, tesseract, octaplex ou polyoctaedron (pO), tetraplex ou politetrahedron (pT) e dodecaplex ou polydodecahedron (pD).

Norman Johnson defendido os nomes n de células, ou pentachoron, hexadecachoron, tesseract ou octachoron, icositetrachoron, hexacosichoron, e hecatonicosachoron (ou dodecacontachoron), cunhar o termo polychoron sendo uma analogia 4D para o poliedro 3D, e polígono 2D, expressa a partir do grego raízes poly ("muitos") e choros ("sala" ou "espaço").

A característica de Euler para todos os 4 politopos é zero, temos o análogo 4-dimensional da fórmula poliédrica de Euler:

${\ displaystyle N_ {0} -N_ {1} + N_ {2} -N_ {3} = 0 \,}$

onde N _k denota o número de k -faces no politopo (um vértice é uma face 0, uma aresta é uma face 1, etc.).

A topologia de qualquer 4 politopo dado é definida por seus números de Betti e coeficientes de torção .

Como configurações

Um 4-politopo regular pode ser completamente descrito como uma matriz de configuração contendo contagens de seus elementos componentes. As linhas e colunas correspondem a vértices, arestas, faces e células. Os números diagonais (superior esquerdo para inferior direito) indicam quantos de cada elemento ocorrem em todo o 4-politopo. Os números não diagonais dizem quantos elementos da coluna ocorrem no ou no elemento da linha. Por exemplo, existem 2 vértices em cada aresta (cada aresta tem 2 vértices) e 2 células se encontram em cada face (cada face pertence a 2 células), em qualquer 4-politopo regular. Observe que a configuração do politopo duplo pode ser obtida girando a matriz em 180 graus.

5 células {3,3,3}	16 células {3,3,4}	tesseract {4,3,3}	24 células {3,4,3}	600 células {3,3,5}	120 células {5,3,3}
${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 5 & 4 & 6 & 4 \\ 2 & 10 & 3 & 3 \\ 3 & 3 & 10 & 2 \\ 4 & 6 & 4 & 5 \ end {matrix}} \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 8 & 6 & 12 & 8 \\ 2 & 24 & 4 & 4 \\ 3 & 3 & 32 & 2 \\ 4 & 6 & 4 & 16 \ end {matrix}} \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 16 & 4 & 6 & 4 \\ 2 & 32 & 3 & 3 \\ 4 & 4 & 24 & 2 \\ 8 & 12 & 6 & 8 \ end {matrix}} \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 24 & 8 & 12 & 6 \\ 2 & 96 & 3 & 3 \\ 3 & 3 & 96 & 2 \\ 6 & 12 & 8 & 24 \ end {matrix}} \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 120 & 12 & 30 & 20 \\ 2 & 720 & 5 & 5 \\ 3 & 3 & 1200 & 2 \\ 4 & 6 & 4 & 600 \ end {matrix}} \ end {bmatrix}}}$	${\ displaystyle {\ begin {bmatrix} {\ begin {matrix} 600 & 4 & 6 & 4 \\ 2 & 1200 & 3 & 3 \\ 5 & 5 & 720 & 2 \\ 20 & 30 & 12 & 120 \ end {matrix}} \ end {bmatrix}}}$

Visualização

A tabela a seguir mostra algumas projeções bidimensionais desses 4 politopos. Várias outras visualizações podem ser encontradas nos links externos abaixo. Os gráficos do diagrama de Coxeter-Dynkin também são fornecidos abaixo do símbolo Schläfli .

A 4 = [3,3,3]	B 4 = [4,3,3]		F 4 = [3,4,3]	H 4 = [5,3,3]
5 células	16 células	8 células	24 células	600 células	120 células
{3,3,3}	{3,3,4}	{4,3,3}	{3,4,3}	{3,3,5}	{5,3,3}
Projeções ortográficas 3D sólidas
Envelope tetraédrico (centrado na célula / vértice)	envelope cúbico (centrado na célula)	Envelope cúbico (centrado na célula)	Envelope cuboctaédrico (centrado na célula)	Envelope icosidodecaédrico de pentakis (centrado no vértice)	Envelope triaconaedro rômbico truncado (centrado na célula)
Diagramas de Wireframe Schlegel ( projeção em perspectiva )
Centrado na célula	Centrado na célula	Centrado na célula	Centrado na célula	Centrado no vértice	Centrado na célula
Projeções estereográficas wireframe ( 3 esferas )

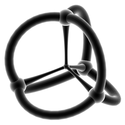
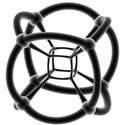
Estrela regular (Schläfli – Hess) 4-politopos

Isso mostra as relações entre os politopos estrelados quadridimensionais. As 2 formas convexas e as 10 formas estreladas podem ser vistas em 3D como os vértices de um cuboctaedro .

Um subconjunto de relações entre 8 formas do polidodecaedro (pD) de 120 células. As três operações {a, g, s} são comutáveis, definindo uma estrutura cúbica. Existem 7 densidades vistas no posicionamento vertical, com 2 formas duais tendo a mesma densidade.

Os Schläfli-Hess 4-polytopes são o conjunto completo de 10 regulares de auto-interseção polychora estrela ( Polytopes quatro dimensões ). Eles são nomeados em homenagem a seus descobridores: Ludwig Schläfli e Edmund Hess . Cada um é representado por um símbolo Schläfli { p , q , r } em que um dos números é5/2. Eles são, portanto, análogos aos poliedros Kepler-Poinsot não convexos regulares , que por sua vez são análogos ao pentagrama.

Nomes

Seus nomes dados aqui foram dados por John Conway , estendendo os nomes de Cayley para os poliedros Kepler-Poinsot : junto com estrelado e ótimo , ele adiciona um grande modificador. Conway ofereceu estas definições operacionais:

1. stellation - substitui bordas por bordas mais longas nas mesmas linhas. (Exemplo: um pentágono estrelado em um pentagrama )
2. engrandecimento - substitui os rostos por outros grandes nos mesmos planos. (Exemplo: um icosaedro se transforma em um grande icosaedro )
3. engrandecimento - substitui as células por outras grandes nos mesmos 3 espaços. (Exemplo: uma célula de 600 se engrandece em uma grande célula de 600 )

John Conway nomeia as 10 formas de 3 4-politopos de células regulares: pT = politetraedro {3,3,5} (um tetraédrico de 600 células ), pI = poliicosedro {3,5,5/2} (uma célula 120 icosaédrica ) e pD = polidodecaedro {5,3,3} (uma célula 120 dodecaédrica ), com modificadores de prefixo: g , a e s para ótimo, (ag) grande e estrelado. A estrelação final, o grande polidodecaedro estrelado, contém todos eles como gaspD .

Simetria

Todos os dez polychora têm [3,3,5] ( H ₄ ) simetria hexacosicórica . Eles são gerados a partir de 6 grupos de simetria de ordem racional de tetraedros de Goursat relacionados : [3,5,5 / 2], [5,5 / 2,5], [5,3,5 / 2], [5 / 2,5 , 5/2], [5,5 / 2,3] e [3,3,5 / 2].

Cada grupo possui 2 estrelas-policora regulares, exceto dois grupos que são autoduais, possuindo apenas um. Portanto, há 4 pares duais e 2 formas autoduais entre as dez estrelas policoras regulares.

Propriedades

Observação:

• Existem 2 arranjos de vértices exclusivos , combinando aqueles de 120 células e 600 células .
• Existem 4 arranjos de arestas exclusivos , que são mostrados como projeções ortográficas de wireframes .
• Existem 7 arranjos de faces exclusivos , mostrados como projeções ortográficas sólidas (da cor da face).

As células (poliedros), suas faces (polígonos), as figuras de arestas poligonais e as figuras de vértices poliédricas são identificadas por seus símbolos Schläfli .

Nome Conway (abrev.)	Projeção ortogonal	Schläfli Coxeter	C {p, q}	F {p}	E {r}	V {q, r}	Dens.	χ
Policosaedro icosaédrico de 120 células (pI)		{3,5,5 / 2}	120 {3,5}	1200 {3}	720 {5/2 }	120 {5,5 / 2}	4	480
Polidodecaedro estrelado pequeno estrelado de 120 células (spD)		{5 / 2,5,3}	120 {5 / 2,5}	720 {5/2}	1200 {3}	120 {5,3}	4	-480
Grande polidodecaedro de 120 células (gpD)		{5,5 / 2,5}	120 {5,5 / 2}	720 {5}	720 {5}	120 {5 / 2,5}	6	0
Grande polidodecaedro de 120 células (apD)		{5,3,5 / 2}	120 {5,3}	720 {5}	720 {5/2}	120 {3,5 / 2}	20	0
Grande polidodecaedro estrelado estrelado de 120 células (gspD)		{5 / 2,3,5}	120 {5 / 2,3}	720 {5/2}	720 {5}	120 {3,5}	20	0
Polidodecaedro grande estrelado de 120 células (aspD)		{5 / 2,5,5 / 2}	120 {5 / 2,5}	720 {5/2}	720 {5/2}	120 {5,5 / 2}	66	0
Grande grande polidodecaedro de 120 células (gapD)		{5,5 / 2,3}	120 {5,5 / 2}	720 {5}	1200 {3}	120 {5 / 2,3}	76	-480
Grande policosaedro icosaédrico de 120 células (gpI)		{3,5 / 2,5}	120 {3,5 / 2}	1200 {3}	720 {5}	120 {5 / 2,5}	76	480
Grande politetraedro de 600 células (apT)		{3,3,5 / 2}	600 {3,3}	1200 {3}	720 {5/2}	120 {3,5 / 2}	191	0
Grande grande polidodecaedro estrelado de 120 células (gaspD)		{5 / 2,3,3}	120 {5 / 2,3}	720 {5/2}	1200 {3}	600 {3,3}	191	0

Veja também

• Politopo regular
• Lista de politopos regulares
• 4 politopos regulares infinitos:
  • Um favo de mel euclidiano regular: {4,3,4}
  • Quatro favos de mel hiperbólicos regulares compactos: {3,5,3}, {4,3,5}, {5,3,4}, {5,3,5}
  • Onze favos de mel hiperbólicos regulares paracompactos: {3,3,6}, {6,3,3}, {3,4,4}, {4,4,3}, {3,6,3}, {4,3 , 6}, {6,3,4}, {4,4,4}, {5,3,6}, {6,3,5} e {6,3,6}.
• 4 politopos regulares abstratos :
  • 11 células {3,5,3}
  • 57 células {5,3,5}
• Famílias uniformes de 4 politopos uniformes de 4 politopos construídas a partir dessas 6 formas regulares.
• Sólido platônico
• Poliedro Kepler-Poinsot - poliedro estrela regular
• Polígono em estrela - polígonos em estrela regulares
• 4 politopo
• 5 politopo
• 6 politopo

Referências

Citações

Bibliografia

links externos

• Weisstein, Eric W. "Regular polychoron" . MathWorld .
• Jonathan Bowers, 16 4 politopos regulares
• Dobras regulares de politopo 4D
• Catálogo de imagens de politopo Uma coleção de projeções estereográficas de 4 politopos.
• Um catálogo de politopos uniformes
• Dimensões Filme de 2 horas sobre a quarta dimensão (contém projeções estereográficas de todos os 4 politopos regulares)
• Olshevsky, George. "Hecatonicosachoron" . Glossário para o hiperespaço . Arquivado do original em 4 de fevereiro de 2007.
  • Olshevsky, George. "Hexacosichoron" . Glossário para o hiperespaço . Arquivado do original em 4 de fevereiro de 2007.
  • Olshevsky, George. "Stellation" . Glossário para o hiperespaço . Arquivado do original em 4 de fevereiro de 2007.
  • Olshevsky, George. "Aumentando" . Glossário para o hiperespaço . Arquivado do original em 4 de fevereiro de 2007.
  • Olshevsky, George. "Engrandecimento" . Glossário para o hiperespaço . Arquivado do original em 4 de fevereiro de 2007.
• Reguläre Polytope
• The Regular Star Polychora
• Hipersólidos