Convolução - Convolution

Comparação visual de convolução, correlação cruzada e autocorrelação . Para as operações envolvendo a função f , e assumindo que a altura de f seja 1,0, o valor do resultado em 5 pontos diferentes é indicado pela área sombreada abaixo de cada ponto. Além disso, a simetria de f é a razão e são idênticas neste exemplo.${\ displaystyle g * f}$${\ displaystyle f \ star g}$

Em matemática (em particular, análise funcional ), a convolução é uma operação matemática em duas funções ( f e g ) que produz uma terceira função ( ) que expressa como a forma de uma é modificado pela outra. O termo convolução se refere à função de resultado e ao processo de computá-la. É definido como a integral do produto das duas funções depois que uma é revertida e deslocada. A integral é avaliada para todos os valores de deslocamento, produzindo a função de convolução. ${\ displaystyle f * g}$

Algumas características da convolução são semelhantes à correlação cruzada : para funções de valor real, de uma variável contínua ou discreta, ela difere da correlação cruzada ( ) apenas porque f ( x ) ou g ( x ) é refletido sobre o y -eixo; portanto, é uma correlação cruzada de f ( x ) e g (- x ) , ou f (- x ) e g ( x ) . Para funções de valor complexo, o operador de correlação cruzada é o adjunto do operador de convolução. ${\ displaystyle f \ star g}$

A convolução tem aplicações que incluem probabilidade , estatística , acústica , espectroscopia , processamento de sinal e processamento de imagem , engenharia , física , visão computacional e equações diferenciais .

A convolução pode ser definida para funções no espaço euclidiano e outros grupos . Por exemplo, funções periódicas , como a transformação de Fourier de tempo discreto , podem ser definidas em um círculo e convolvidas por convolução periódica . (Consulte a linha 18 em DTFT § Properties .) Uma convolução discreta pode ser definida para funções no conjunto de inteiros .

As generalizações de convolução têm aplicações no campo da análise numérica e álgebra linear numérica e no projeto e implementação de filtros de resposta a impulso finito no processamento de sinais.

O cálculo do inverso da operação de convolução é conhecido como deconvolução .

Definição

A convolução de f e g é escrito f * g , denotando o operador com o símbolo * . É definido como a integral do produto das duas funções depois que uma é revertida e deslocada. Como tal, é um tipo particular de transformação integral :

${\ displaystyle (f * g) (t): = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) \, d \ tau.}$

Uma definição equivalente é (ver comutatividade ):

${\ displaystyle (f * g) (t): = \ int _ {- \ infty} ^ {\ infty} f (t- \ tau) g (\ tau) \, d \ tau.}$

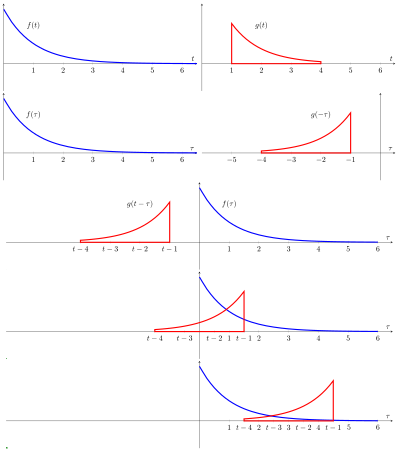
Embora o símbolo t seja usado acima, ele não precisa representar o domínio do tempo. Mas, nesse contexto, a fórmula de convolução pode ser descrita como a área sob a função f ( τ ) ponderada pela função g (- τ ) deslocada pela quantidade t . À medida que t muda, a função de ponderação g ( t - τ ) enfatiza diferentes partes da função de entrada f ( τ ) .

Para funções f , g suportadas apenas em [0, ∞) (ou seja, zero para argumentos negativos), os limites de integração podem ser truncados, resultando em:

${\ displaystyle (f * g) (t) = \ int _ {0} ^ {t} f (\ tau) g (t- \ tau) \, d \ tau \ quad \ {\ text {for}} f , g: [0, \ infty) \ to \ mathbb {R}.}$

Para a formulação multidimensional da convolução, consulte o domínio de definição (abaixo).

Notação

Uma convenção comum de notação de engenharia é:

${\ displaystyle f (t) * g (t) \ mathrel {: =} \ underbrace {\ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) \, d \ tau} _ {(f * g) (t)},}$

que deve ser interpretado com cuidado para evitar confusão. Por exemplo, f ( t ) ∗ g ( t - t ₀ ) é equivalente a ( f ∗ g ) ( t - t ₀ ) , mas f ( t - t ₀ ) ∗ g ( t - t ₀ ) é de fato equivalente a ( f ∗ g ) ( t - 2 t ₀ ) .

Derivações

A convolução descreve a saída (em termos de entrada) de uma importante classe de operações conhecida como linear invariante no tempo (LTI). Consulte a teoria do sistema LTI para obter uma derivação da convolução como resultado das restrições LTI. Em termos das transformadas de Fourier da entrada e saída de uma operação LTI, nenhum novo componente de frequência é criado. Os existentes são apenas modificados (amplitude e / ou fase). Em outras palavras, a transformação de saída é o produto pontual da transformação de entrada com uma terceira transformação (conhecida como função de transferência ). Veja o teorema da convolução para uma derivação dessa propriedade de convolução. Por outro lado, a convolução pode ser derivada como a transformada de Fourier inversa do produto pontual de duas transformadas de Fourier.

Explicação visual

Expresse cada função em termos de uma variável fictícia ${\ displaystyle \ tau.}$ Reflita uma das funções: →${\ displaystyle g (\ tau)}$${\ displaystyle g (- \ tau).}$ Adicione um deslocamento de tempo, t , que permite deslizar ao longo do eixo.${\ displaystyle g (t- \ tau)}$${\ displaystyle \ tau}$ Comece t em −∞ e deslize-o totalmente para + ∞ . Onde quer que as duas funções se cruzem, encontre a integral de seu produto. Em outras palavras, no tempo t , calcule a área sob a função ponderada pela função de ponderação${\ displaystyle f (\ tau)}$${\ displaystyle g (t- \ tau).}$ A forma de onda resultante (não mostrada aqui) é a convolução das funções f e g . Se f ( t ) é um impulso unitário , o resultado desse processo é simplesmente g ( t ) . Formalmente: ${\ displaystyle \ int _ {- \ infty} ^ {\ infty} \ delta (\ tau) g (t- \ tau) \, d \ tau = g (t)}$
Neste exemplo, o "pulso" de cor vermelha é uma função par, portanto a convolução é equivalente à correlação. Um instantâneo deste "filme" mostra funções e (em azul) para algum valor de parâmetro que é arbitrariamente definido como a distância do eixo ao centro do pulso vermelho. A quantidade de amarelo é a área do produto calculada pela integral de convolução / correlação. O filme é criado alterando e recalculando continuamente o integral. O resultado (mostrado em preto) é uma função de, mas é plotado no mesmo eixo para conveniência e comparação. ${\ displaystyle \ g (\ tau),}$ ${\ displaystyle (\ g (- \ tau) = g (\ tau) \),}$${\ displaystyle g (t- \ tau)}$${\ displaystyle f (\ tau)}$${\ displaystyle t,}$${\ displaystyle \ tau = 0}$${\ displaystyle f (\ tau) \ cdot g (t- \ tau),}$${\ displaystyle t}$${\ displaystyle t,}$${\ displaystyle \ tau,}$
Nesta representação, poderia representar a resposta de um circuito RC a um pulso estreito que ocorre em Em outras palavras, se o resultado da convolução for justo Mas quando é o pulso mais largo (em vermelho), a resposta é uma versão "manchada" de Ele começa em porque definimos como a distância do eixo ao centro do pulso largo (em vez da borda de ataque). ${\ displaystyle f (\ tau)}$${\ displaystyle \ tau = 0.}$${\ displaystyle g (\ tau) = \ delta (\ tau),}$${\ displaystyle f (t).}$${\ displaystyle g (\ tau)}$${\ displaystyle f (t).}$${\ displaystyle t = -0,5,}$${\ displaystyle t}$${\ displaystyle \ tau = 0}$

Desenvolvimentos históricos

Um dos primeiros usos da integral de convolução apareceu na derivação de D'Alembert do teorema de Taylor em Recherches sur différents points importants du système du monde, publicado em 1754.

Além disso, uma expressão do tipo:

${\ displaystyle \ int f (u) \ cdot g (xu) \, du}$

é usado por Sylvestre François Lacroix na página 505 de seu livro intitulado Tratado sobre diferenças e série , que é o último dos 3 volumes da série enciclopédica: Traité du calcul différentiel et du calcul intégral , Chez Courcier, Paris, 1797-1800. Logo depois disso, as operações de convolução aparecem nas obras de Pierre Simon Laplace , Jean-Baptiste Joseph Fourier , Siméon Denis Poisson e outros. O próprio termo não se tornou amplamente utilizado até os anos 1950 ou 1960. Antes de que foi, por vezes, conhecido como Faltung (cujos meios dobráveis em alemão ), produto da composição , integrante sobreposição , e integrante de Carson . No entanto, ele aparece já em 1903, embora a definição seja bastante desconhecida em usos mais antigos.

A operação:

${\ displaystyle \ int _ {0} ^ {t} \ varphi (s) \ psi (ts) \, ds, \ quad 0 \ leq t <\ infty,}$

é um caso particular de produtos de composição considerados pelo matemático italiano Vito Volterra em 1913.

Convolução circular

Quando uma função g _T é periódica, com período T , então para funções, f , tal que f ∗ g _T existe, a convolução também é periódica e idêntica a:

${\ displaystyle (f * g_ {T}) (t) \ equiv \ int _ {t_ {0}} ^ {t_ {0} + T} \ left [\ sum _ {k = - \ infty} ^ {\ infty} f (\ tau + kT) \ right] g_ {T} (t- \ tau) \, d \ tau,}$

onde t ₀ é uma escolha arbitrária. O somatório é denominado somatório periódico da função f .

Quando g _T é uma soma periódica de outra função, g , então f ∗ g _T é conhecido como uma convolução circular ou cíclica de f e g .

E se o somatório periódica acima é substituído por f _T , a operação é chamada um periódica convolução de f _{o t} e g _t .

Convolução discreta

Para funções de valor complexo f , g definidas no conjunto Z de inteiros, a convolução discreta de f e g é dada por:

${\ displaystyle (f * g) [n] = \ sum _ {m = - \ infty} ^ {\ infty} f [m] g [nm],}$

ou equivalentemente (ver comutatividade ) por:

${\ displaystyle (f * g) [n] = \ sum _ {m = - \ infty} ^ {\ infty} f [nm] g [m].}$

A convolução de duas sequências finitas é definida pela extensão das sequências para funções com suporte finito no conjunto de inteiros. Quando as sequências são os coeficientes de dois polinômios , então os coeficientes do produto comum dos dois polinômios são a convolução das duas sequências originais. Isso é conhecido como o produto de Cauchy dos coeficientes das sequências.

Assim, quando g tem suporte finito no conjunto (representando, por exemplo, uma resposta de impulso finita ), uma soma finita pode ser usada: ${\ displaystyle \ {- M, -M + 1, \ dots, M-1, M \}}$

${\ displaystyle (f * g) [n] = \ sum _ {m = -M} ^ {M} f [nm] g [m].}$

Convolução discreta circular

Quando uma função g _N é periódica, com período N , então para funções, f , tal que f ∗ g _N existe, a convolução também é periódica e idêntica a:

${\ displaystyle (f * g_ {N}) [n] \ equiv \ sum _ {m = 0} ^ {N-1} \ left (\ sum _ {k = - \ infty} ^ {\ infty} {f } [m + kN] \ right) g_ {N} [nm].}$

A soma em k é chamada de soma periódica da função f .

Se g _N é uma soma periódica de outra função, g , então f ∗ g _N é conhecido como uma convolução circular de f e g .

Quando as durações diferentes de zero de f e g são limitadas ao intervalo [0, N - 1] ,  f ∗ g _{N se} reduz a estas formas comuns:

${\ displaystyle {\ begin {alinhado} \ left (f * g_ {N} \ right) [n] & = \ sum _ {m = 0} ^ {N-1} f [m] g_ {N} [nm ] \\ & = \ sum _ {m = 0} ^ {n} f [m] g [nm] + \ sum _ {m = n + 1} ^ {N-1} f [m] g [N + nm] \\ [2pt] & = \ sum _ {m = 0} ^ {N-1} f [m] g [(nm) _ {\ bmod {N}}] \\ [2pt] & \ triangleq \ esquerda (f * _ {N} g \ direita) [n] \ end {alinhado}}}$

( Eq.1 )

A notação ( f * _N g ) para cíclico convolução denota convolução sobre o grupo cíclico de inteiros módulo N .

A convolução circular surge mais frequentemente no contexto de convolução rápida com um algoritmo de transformada rápida de Fourier (FFT).

Algoritmos de convolução rápida

Em muitas situações, convoluções discretas podem ser convertidas em circulares de modo que as transformações rápidas com uma propriedade de convolução possam ser usadas para implementar o cálculo. Por exemplo, a convolução de sequências de dígitos é a operação de kernel na multiplicação de números de vários dígitos, que pode, portanto, ser implementada de forma eficiente com técnicas de transformação ( Knuth 1997 , §4.3.3.C; von zur Gathen & Gerhard 2003 , §8.2).

A Eq.1 requer N operações aritméticas por valor de saída e N ² operações para N saídas. Isso pode ser reduzido significativamente com qualquer um dos vários algoritmos rápidos. O processamento digital de sinais e outras aplicações normalmente usam algoritmos de convolução rápida para reduzir o custo da convolução para acomplexidadeO ( N log N ).

Os algoritmos de convolução rápida mais comuns usam algoritmos de transformada rápida de Fourier (FFT) por meio do teorema da convolução circular . Especificamente, a convolução circular de duas sequências de comprimento finito é encontrada tomando uma FFT de cada sequência, multiplicando pontualmente e, em seguida, executando uma FFT inversa. As convoluções do tipo definido acima são então eficientemente implementadas usando essa técnica em conjunto com a extensão zero e / ou descartando porções da saída. Outros algoritmos de convolução rápida, como o algoritmo Schönhage-Strassen ou a transformada de Mersenne, usam transformadas rápidas de Fourier em outros anéis .

Se uma sequência for muito mais longa do que a outra, a extensão zero da sequência mais curta e a convolução circular rápida não é o método mais eficiente computacionalmente disponível. Em vez disso, decompor a sequência mais longa em blocos e convolver cada bloco permite algoritmos mais rápidos, como o método overlap-save e o método overlap-add . Um método de convolução híbrido que combina algoritmos de bloco e FIR permite uma latência de entrada-saída zero que é útil para cálculos de convolução em tempo real.

Domínio de definição

A convolução de duas funções de valor complexo em R ^d é ela própria uma função de valor complexo em R ^d , definida por:

${\ displaystyle (f * g) (x) = \ int _ {\ mathbf {R} ^ {d}} f (y) g (xy) \, dy = \ int _ {\ mathbf {R} ^ {d }} f (xy) g (y) \, dy,}$

e é bem definida somente se f e g decaimento de maneira suficientemente rápida no infinito, para o integrante de existir. As condições para a existência da convolução podem ser complicadas, uma vez que uma explosão em g no infinito pode ser facilmente compensada por um declínio suficientemente rápido em f . A questão da existência, portanto, pode envolver diferentes condições em f e g :

Funções com suporte compacto

Se f e g são compactamente suportado funções continuas , então a sua convoluo existente, e é também suportada de forma compacta e contínua ( Hörmander 1983 , Capítulo 1). De maneira mais geral, se uma das funções (digamos f ) for compactamente suportada e a outra for localmente integrável , então a convolução f ∗ g é bem definida e contínua.

Convolução de f e g é também bem definida quando ambas as funções são localmente quadrado integrável em R e suportado num intervalo da forma [ a , + ∞) (ou ambos suportados [-∞, um ] ).

Funções integráveis

A convolução de f e g existe se f e g são ambos funções integráveis Lebesgue em L ¹ ( R ^d ) , e, neste caso, f * g também é integrável ( Stein & Weiss, 1971 , Teorema 1,3). Isso é uma consequência do teorema de Tonelli . Isso também é verdadeiro para funções em L ¹ , sob a convolução discreta ou, mais geralmente, para a convolução em qualquer grupo .

Da mesma forma, se f ∈ L ¹ ( R ^d ) e   g ∈ L ^p ( R ^d ) onde 1 ≤ p ≤ ∞ , então   f ∗ g ∈ L ^p ( R ^d ), e

${\ displaystyle \ | {f} * g \ | _ {p} \ leq \ | f \ | _ {1} \ | g \ | _ {p}.}$

No caso particular p = 1 , isto mostra que L ¹ é uma álgebra Banach sob a convolução (e igualdade dos dois lados se mantém f e g são não-negativo quase em toda a parte).

De maneira mais geral, a desigualdade de Young implica que a convolução é um mapa bilinear contínuo entre espaços L ^p adequados . Especificamente, se 1 ≤ p , q , r ≤ ∞ satisfaça:

${\ displaystyle {\ frac {1} {p}} + {\ frac {1} {q}} = {\ frac {1} {r}} + 1,}$

então

${\ displaystyle \ left \ Vert f * g \ right \ Vert _ {r} \ leq \ left \ Vert f \ right \ Vert _ {p} \ left \ Vert g \ right \ Vert _ {q}, \ quad f \ in {\ mathcal {L}} ^ {p}, \ g \ in {\ mathcal {L}} ^ {q},}$

de modo que a convolução é um mapeamento bilinear contínuo de L ^p × L ^q a L ^r . A desigualdade de Young para convolução também é verdadeira em outros contextos (grupo de círculo, convolução em Z ). A desigualdade anterior não é nítida na linha real: quando 1 < p , q , r <∞ , existe uma constante B _{p , q} <1 tal que:

${\ displaystyle \ left \ Vert f * g \ right \ Vert _ {r} \ leq B_ {p, q} \ left \ Vert f \ right \ Vert _ {p} \ left \ Vert g \ right \ Vert _ { q}, \ quad f \ in {\ mathcal {L}} ^ {p}, \ g \ in {\ mathcal {L}} ^ {q}.}$

O valor ótimo de B _{p , q} foi descoberto em 1975 e de forma independente em 1976, veja a desigualdade de Brascamp-Lieb .

Uma estimativa mais forte é verdadeira, desde que 1 < p , q , r <∞ :

${\ displaystyle \ | f * g \ | _ {r} \ leq C_ {p, q} \ | f \ | _ {p} \ | g \ | _ {q, w}}$

onde está a norma L ^q fraca . A convolução também define um mapa contínuo bilinear para , devido à fraca desigualdade de Young: ${\ displaystyle \ | g \ | _ {q, w}}$${\ displaystyle L ^ {p, w} \ times L ^ {q, w} \ a L ^ {r, w}}$${\ displaystyle 1 <p, q, r <\ infty}$

${\ displaystyle \ | f * g \ | _ {r, w} \ leq C_ {p, q} \ | f \ | _ {p, w} \ | g \ | _ {r, w}.}$

Funções de decadência rápida

Além de funções com suporte compacto e funções integráveis, funções que têm decaimento suficientemente rápido no infinito também podem ser convolvidas. Uma característica importante da convolução é que se f e g decaem rapidamente, então f ∗ g também decai rapidamente. Em particular, se f e g são diminuindo rapidamente funções , então também o é a convolução f * g . Combinado com o fato de que convolução comuta com diferenciação (veja #Properties ), segue-se que a classe de funções de Schwartz é fechada sob convolução ( Stein & Weiss 1971 , Teorema 3.3).

Distribuições

Em algumas circunstâncias, é possível definir a convolução de uma função com uma distribuição ou de duas distribuições. Se f é uma função compactamente suportada e g é uma distribuição, então f ∗ g é uma função suave definida por uma fórmula de distribuição análoga a

${\ displaystyle \ int _ {\ mathbf {R} ^ {d}} {f} (y) g (xy) \, dy.}$

De forma mais geral, é possível estender a definição da convolução de uma maneira única para que a lei associativa

${\ displaystyle f * (g * \ varphi) = (f * g) * \ varphi}$

permanece válido no caso em que f é uma distribuição eg uma distribuição compactamente suportada ( Hörmander 1983 , §4.2).

Medidas

A convolução de quaisquer duas medidas de Borel μ e ν de variação limitada é a medida definida por ( Rudin 1962 ) ${\ displaystyle \ mu * \ nu}$

${\ displaystyle \ int _ {\ mathbf {R} ^ {d}} f (x) \, d (\ mu * \ nu) (x) = \ int _ {\ mathbf {R} ^ {d}} \ int _ {\ mathbf {R} ^ {d}} f (x + y) \, d \ mu (x) \, d \ nu (y).}$

Em particular,

${\ displaystyle (\ mu * \ nu) (A) = \ int _ {\ mathbf {R} ^ {d} \ times \ mathbf {R} ^ {d}} 1_ {A} (x + y) \, d (\ mu \ vezes \ nu) (x, y),}$

onde é um conjunto mensurável e é a função de indicador de . ${\ displaystyle A \ subset \ mathbf {R} ^ {d}}$${\ displaystyle 1_ {A}}$${\ displaystyle A}$

Isso está de acordo com a convolução definida acima quando μ e ν são considerados como distribuições, bem como a convolução das funções L ¹ quando μ e ν são absolutamente contínuos em relação à medida de Lebesgue.

A convolução das medidas também satisfaz a seguinte versão da desigualdade de Young

${\ displaystyle \ | \ mu * \ nu \ | \ leq \ | \ mu \ | \ | \ nu \ |}$

onde a norma é a variação total de uma medida. Como o espaço de medidas de variação limitada é um espaço de Banach , a convolução de medidas pode ser tratada com métodos padrão de análise funcional que podem não se aplicar à convolução de distribuições.

Propriedades

Propriedades algébricas

A convolução define um produto no espaço linear de funções integráveis. Este produto satisfaz as seguintes propriedades algébricas, que formalmente significam que o espaço de funções integráveis ​​com o produto dado pela convolução é uma álgebra associativa comutativa sem identidade ( Strichartz 1994 , §3.3). Outros espaços lineares de funções, como o espaço de funções contínuas de suporte compacto, são fechados sob a convolução e, portanto, também formam álgebras associativas comutativas.

Comutatividade

$${\ displaystyle f * g = g * f}$$

Prova: Por definição:

$${\ displaystyle (f * g) (t) = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) \, d \ tau}$$

A seguir, alterando a variável de integração para o resultado.${\ displaystyle u = t- \ tau}$

Associatividade

$${\ displaystyle f * (g * h) = (f * g) * h}$$

Prova: Isso decorre do uso do teorema de Fubini (isto é, integrais duplos podem ser avaliados como integrais iterados em qualquer ordem).

Distributividade

$${\ displaystyle f * (g + h) = (f * g) + (f * h)}$$

Prova: Isso decorre da linearidade da integral.

Associatividade com multiplicação escalar

$${\ displaystyle a (f * g) = (af) * g}$$

para qualquer número real (ou complexo) .${\ displaystyle a}$

Identidade multiplicativa

Nenhuma álgebra de funções possui uma identidade para a convolução. A falta de identidade normalmente não é um grande inconveniente, uma vez que a maioria das coleções de funções nas quais a convolução é realizada podem ser convolvidas com uma distribuição delta (um impulso unitário, centrado em zero) ou, pelo menos (como é o caso de L ¹ ) admitir aproximações à identidade . O espaço linear de distribuições compactamente suportadas, entretanto, admite uma identidade sob a convolução. Especificamente,

$${\ displaystyle f * \ delta = f}$$

onde δ é a distribuição delta.

Elemento inverso

Algumas distribuições S têm um elemento inverso S ⁻¹ para a convolução que então deve satisfazer

$${\ displaystyle S ^ {- 1} * S = \ delta}$$

a partir da qual uma fórmula explícita para S ⁻¹ pode ser obtida.

O conjunto de distribuições invertíveis forma um grupo abeliano sob a convolução.

Conjugação complexa

${\ displaystyle {\ overline {f * g}} = {\ overline {f}} * {\ overline {g}}}$

Relação com diferenciação

$${\ displaystyle (f * g) '= f' * g = f * g '}$$

Prova:

$${\ displaystyle {\ begin {align} (f * g) '& = {\ frac {d} {dt}} \ int _ {- \ infty} ^ {\ infty} f (\ tau) g (t- \ tau) \, d \ tau \\ [4pt] & = \ int _ {- \ infty} ^ {\ infty} f (\ tau) {\ frac {\ partial} {\ partial t}} g (t- \ tau) \, d \ tau \\ [4pt] & = \ int _ {- \ infty} ^ {\ infty} f (\ tau) g '(t- \ tau) \, d \ tau = f * g' . \ end {alinhado}}}$$

Relacionamento com integração

Se e então${\ textstyle F (t) = \ int _ {- \ infty} ^ {t} f (\ tau) d \ tau,}$${\ textstyle G (t) = \ int _ {- \ infty} ^ {t} g (\ tau) \, d \ tau,}$

$${\ displaystyle (F * g) (t) = (f * G) (t) = \ int _ {- \ infty} ^ {t} (f * g) (\ tau) \, d \ tau.}$$

Integração

Se f e g são funções integráveis, em seguida, o integrante da sua convolução em todo o espaço é simplesmente obtido como o produto de suas integrais:

${\ displaystyle \ int _ {\ mathbf {R} ^ {d}} (f * g) (x) \, dx = \ left (\ int _ {\ mathbf {R} ^ {d}} f (x) \, dx \ right) \ left (\ int _ {\ mathbf {R} ^ {d}} g (x) \, dx \ right).}$

Isso decorre do teorema de Fubini . O mesmo resultado é válido se f e g são considerados apenas para ser funções mensuráveis não-negativos, por teorema de Tonelli .

Diferenciação

No caso de uma variável,

${\ displaystyle {\ frac {d} {dx}} (f * g) = {\ frac {df} {dx}} * g = f * {\ frac {dg} {dx}}}$

onde d / dx é a derivada . De forma mais geral, no caso de funções de várias variáveis, uma fórmula análoga é válida para a derivada parcial :

${\ displaystyle {\ frac {\ partial} {\ partial x_ {i}}} (f * g) = {\ frac {\ partial f} {\ partial x_ {i}}} * g = f * {\ frac {\ parcial g} {\ parcial x_ {i}}}.}$

Uma consequência desta situação é que a convolução pode ser visto como uma operação de "alisamento": a convolução de f e g é diferenciável tantas vezes quanto f e g são, no total.

Estas identidades mantenha sob a condição exacta que f e g são absolutamente integrável e pelo menos um deles tem um absolutamente integrável (L ¹ ) derivado fraco, como consequência da desigualdade de convolução de Young . Por exemplo, quando f é continuamente diferenciável com suporte compacto eg é uma função arbitrária localmente integrável,

${\ displaystyle {\ frac {d} {dx}} (f * g) = {\ frac {df} {dx}} * g.}$

Essas identidades também se aplicam de forma muito mais ampla no sentido de distribuições temperadas se uma de f ou g for uma distribuição temperada de decréscimo rápido , uma distribuição temperada compactamente suportada ou uma função de Schwartz e a outra for uma distribuição temperada. Por outro lado, duas funções integráveis ​​positivas e infinitamente diferenciáveis ​​podem ter uma convolução contínua em lugar nenhum.

No caso discreto, o operador de diferença D f ( n ) = f ( n + 1) - f ( n ) satisfaz uma relação análoga:

${\ displaystyle D (f * g) = (Df) * g = f * (Dg).}$

Teorema de convolução

O teorema da convolução afirma que

${\ displaystyle {\ mathcal {F}} \ {f * g \} = k \ cdot {\ mathcal {F}} \ {f \} \ cdot {\ mathcal {F}} \ {g \}}$

onde denota a transformada de Fourier de , e é uma constante que depende da normalização específica da transformada de Fourier. Versões deste teorema também conter para a transformar Laplace , Transformada de Laplace bilateral , Z-transform e Mellin transformam . ${\ displaystyle {\ mathcal {F}} \ {f \}}$${\ displaystyle f}$${\ displaystyle k}$

Por outro lado, se for a matriz da transformada de Fourier , então ${\ displaystyle {\ mathcal {W}}}$

${\ displaystyle {\ mathcal {W}} \ left (C ^ {(1)} x \ ast C ^ {(2)} y \ right) = \ left ({\ mathcal {W}} C ^ {(1 )} \ bullet {\ mathcal {W}} C ^ {(2)} \ right) (x \ otimes y) = {\ mathcal {W}} C ^ {(1)} x \ circ {\ mathcal {W }} C ^ {(2)} y}$,

onde está o produto de divisão de face , denota o produto Kronecker , denota o produto Hadamard (este resultado é uma evolução das propriedades do esboço de contagem ). ${\ displaystyle \ bullet}$${\ displaystyle \ otimes}$${\ displaystyle \ circ}$

Equivariância translacional

A convolução comuta com traduções, o que significa que

${\ displaystyle \ tau _ {x} (f * g) = (\ tau _ {x} f) * g = f * (\ tau _ {x} g)}$

onde τ _x f é a tradução da função f por x definida por

${\ displaystyle (\ tau _ {x} f) (y) = f (yx).}$

Se f é uma função de Schwartz , então τ _x f é a convolução com uma função delta de Dirac traduzida τ _x f = f ∗ τ _x δ . Assim, a invariância de translação da convolução das funções de Schwartz é uma consequência da associatividade da convolução.

Além disso, sob certas condições, a convolução é a operação invariante de tradução mais geral. Falando informalmente, o seguinte é válido

Suponha que S seja um operador linear limitado agindo sobre funções que comutam com translações: S ( τ _x f ) = τ _x ( Sf ) para todo x . Então S é dado como convolução com uma função (ou distribuição) g _S ; isto é Sf = g _S ∗ f .

Assim, algumas operações invariantes de tradução podem ser representadas como convolução. As convoluções desempenham um papel importante no estudo de sistemas invariantes no tempo e , especialmente , na teoria do sistema LTI . O que representa a função g _S é a resposta ao impulso da transformação S .

Uma versão mais precisa do teorema citado acima requer a especificação da classe de funções na qual a convolução é definida e também requer a suposição de que S deve ser um operador linear contínuo com respeito à topologia apropriada . Sabe-se, por exemplo, que todo operador linear contínuo invariante à translação contínua em L ¹ é a convolução com medida de Borel finita . Mais geralmente, todo operador linear contínuo invariante de translação contínua em L ^p para 1 ≤ p <∞ é a convolução com uma distribuição temperada cuja transformada de Fourier é limitada. A saber, todos eles são dados por multiplicadores de Fourier limitados .

Convoluções em grupos

Se G é um grupo adequado dotado de uma medida λ, e se f e g são funções integráveis reais ou complexas de valor em G , então podemos definir sua convolução por

${\ displaystyle (f * g) (x) = \ int _ {G} f (y) g \ left (y ^ {- 1} x \ right) \, d \ lambda (y).}$

Não é comutativo em geral. Em casos típicos de interesse, G é um grupo topológico localmente compacto de Hausdorff e λ é uma medida de Haar (à esquerda) . Nesse caso, a menos que G seja unimodular , a convolução definida desta forma não é a mesma que . A preferência de um sobre o outro é feita de modo que a convolução com uma função fixa g comute com a translação à esquerda no grupo: ${\ textstyle \ int f \ left (xy ^ {- 1} \ right) g (y) \, d \ lambda (y)}$

${\ displaystyle L_ {h} (f * g) = (L_ {h} f) * g.}$

Além disso, a convenção também é necessária para que haja consistência com a definição de convolução de medidas apresentada a seguir. No entanto, com uma medida de Haar à direita em vez de à esquerda, a última integral tem preferência sobre a primeira.

Em grupos abelianos localmente compactos , uma versão do teorema da convolução é válida: a transformada de Fourier de uma convolução é o produto pontual das transformadas de Fourier. O grupo de círculo T com a medida de Lebesgue é um exemplo imediato. Para um g fixo em L ¹ ( T ), temos o seguinte operador familiar agindo no espaço de Hilbert L ² ( T ):

${\ displaystyle T {f} (x) = {\ frac {1} {2 \ pi}} \ int _ {\ mathbf {T}} {f} (y) g (xy) \, dy.}$

O operador T é compacto . Um cálculo direto mostra que seu T * adjacente é convolução com

${\ displaystyle {\ bar {g}} (- y).}$

Pela propriedade de comutatividade citada acima, T é normal : T * T = TT *. Além disso, T comuta com os operadores de tradução. Considere a família S de operadores que consiste em todas essas convoluções e os operadores de tradução. Então S é uma família de operadores normais que se deslocam diariamente. De acordo com a teoria espectral , existe uma base ortonormal { h _k } que diagonaliza S simultaneamente . Isso caracteriza as convoluções no círculo. Especificamente, temos

${\ displaystyle h_ {k} (x) = e ^ {ikx}, \ quad k \ in \ mathbb {Z}, \;}$

que são precisamente os caracteres de T . Cada convolução é um operador de multiplicação compacto nesta base. Isso pode ser visto como uma versão do teorema da convolução discutido acima.

Um exemplo discreto é um grupo cíclico finito de ordem n . Os operadores de convolução são aqui representados por matrizes circulantes e podem ser diagonalizados pela transformada discreta de Fourier .

Um resultado semelhante é válido para grupos compactos (não necessariamente abelianos): os coeficientes da matriz de representações unitárias de dimensão finita formam uma base ortonormal em L ² pelo teorema de Peter-Weyl , e um análogo do teorema da convolução continua a ser, junto com muitos outros aspectos da análise harmônica que dependem da transformada de Fourier.

Convolução de medidas

Seja G um grupo topológico (escrito multiplicativamente). Se μ e ν são medidas de Borel finitas em G , então sua convolução μ ∗ ν é definida como a medida pushforward da ação do grupo e pode ser escrita como

${\ displaystyle (\ mu * \ nu) (E) = \ iint 1_ {E} (xy) \, d \ mu (x) \, d \ nu (y)}$

para cada subconjunto mensurável E de L . A convolução também é uma medida finita, cuja variação total satisfaz

${\ displaystyle \ | \ mu * \ nu \ | \ leq \ left \ | \ mu \ right \ | \ left \ | \ nu \ right \ |.}$

No caso em que G é localmente compacto com (esquerda-) medida Haar λ, e μ e ν são absolutamente contínuos em relação a λ, de modo que cada um tem uma função de densidade , então a convolução μ ∗ ν também é absolutamente contínua, e sua função de densidade é apenas a convolução das duas funções de densidade separadas.

Se μ e ν são medidas de probabilidade no grupo topológico ( R , +), então a convolução μ ∗ ν é a distribuição de probabilidade da soma X + Y de duas variáveis ​​aleatórias independentes X e Y cujas respectivas distribuições são μ e ν.

Bialgebras

Seja ( X , Δ, ∇, ε , η ) uma bialgebra com comultiplicação Δ, multiplicação ∇, unidade η e contagem ε . A convolução é um produto definido na álgebra do endomorfismo End ( X ) como segue. Seja φ , ψ ∈ End ( X ), ou seja, φ , ψ : X → X são funções que respeitam toda a estrutura algébrica de X , então a convolução φ ∗ ψ é definida como a composição

${\ displaystyle X \ mathrel {\ xrightarrow {\ Delta}} X \ otimes X \ mathrel {\ xrightarrow {\ phi \ otimes \ psi}} X \ otimes X \ mathrel {\ xrightarrow {\ nabla}} X.}$

A convolução aparece notavelmente na definição de álgebras de Hopf ( Kassel 1995 , §III.3). Uma bialgebra é uma álgebra de Hopf se e somente se tiver um antípoda: um endomorfismo S tal que

${\ displaystyle S * \ operatorname {id} _ {X} = \ operatorname {id} _ {X} * S = \ eta \ circ \ varepsilon.}$

Formulários

O desfoque gaussiano pode ser usado para obter uma imagem digital em tons de cinza suave de uma impressão em meio - tom .

Convolução e operações relacionadas são encontradas em muitas aplicações em ciências, engenharia e matemática.

• Em processamento de imagem

  No processamento de imagens digitais, a filtragem convolucional desempenha um papel importante em muitos algoritmos importantes na detecção de bordas e processos relacionados.

  Em óptica , uma fotografia fora de foco é uma convolução da imagem nítida com uma função de lente. O termo fotográfico para isso é bokeh .

  Em aplicativos de processamento de imagem, como adicionar desfoque.

• Em processamento digital de dados

  Em química analítica , os filtros de suavização Savitzky – Golay são usados ​​para a análise de dados espectroscópicos. Eles podem melhorar a relação sinal-ruído com distorção mínima dos espectros

  Em estatística , uma média móvel ponderada é uma convolução.

• Na acústica , a reverberação é a convolução do som original com ecos de objetos ao redor da fonte sonora.

  No processamento de sinal digital, a convolução é usada para mapear a resposta ao impulso de uma sala real em um sinal de áudio digital.

  Na música eletrônica, a convolução é a imposição de uma estrutura espectral ou rítmica em um som. Freqüentemente, esse envelope ou estrutura é obtido de outro som. A convolução de dois sinais é a filtragem de um pelo outro.

• Na engenharia elétrica , a convolução de uma função (o sinal de entrada ) com uma segunda função (a resposta ao impulso) dá a saída de um sistema linear invariante no tempo (LTI). Em qualquer momento, a saída é um efeito acumulado de todos os valores anteriores da função de entrada, com os valores mais recentes normalmente tendo a maior influência (expressa como um fator multiplicativo). A função de resposta ao impulso fornece esse fator como uma função do tempo decorrido desde que ocorreu cada valor de entrada.
• Na física , onde quer que exista um sistema linear com um " princípio de superposição ", surge uma operação de convolução. Por exemplo, na espectroscopia , o alargamento da linha devido ao efeito Doppler por si só dá uma forma de linha espectral Gaussiana e o alargamento de colisão sozinho dá uma forma de linha Lorentziana . Quando ambos os efeitos estão operativos, a forma da linha é uma convolução de Gaussiana e Lorentziana, uma função Voigt .

  Na espectroscopia de fluorescência resolvida no

  tempo , o sinal de excitação pode ser tratado como uma cadeia de pulsos delta e a fluorescência medida é uma soma de decaimentos exponenciais de cada pulso delta.
  Na dinâmica de fluidos computacional , o
  modelo de turbulência de simulação de grande redemoinho (LES) usa a operação de convolução para diminuir a faixa de escalas de comprimento necessárias na computação, reduzindo assim o custo computacional.
• Na teoria da probabilidade , a distribuição de probabilidade da soma de duas variáveis ​​aleatórias independentes é a convolução de suas distribuições individuais.

  Na estimativa da densidade do kernel , uma distribuição é estimada a partir de pontos de amostra por convolução com um kernel, como um Gaussiano isotrópico.

• Em sistemas de planejamento de tratamento de radioterapia, a maior parte de todos os códigos modernos de cálculo aplica um algoritmo de convolução-superposição .
• Na confiabilidade estrutural, o índice de confiabilidade pode ser definido com base no teorema da convolução.

  A definição do índice de confiabilidade para funções de estado limite com distribuições não normais pode ser estabelecida correspondendo à função de distribuição conjunta . Na verdade, a função de distribuição conjunta pode ser obtida usando a teoria da convolução.

• As redes neurais convolucionais aplicam vários núcleos de convolução em cascata com aplicações em visão de máquina e inteligência artificial . Embora essas sejam, na verdade , correlações cruzadas em vez de convoluções na maioria dos casos.
• Na hidrodinâmica de partículas suavizadas , as simulações da dinâmica dos fluidos são calculadas usando partículas, cada uma com núcleos circundantes. Para qualquer partícula dada , alguma quantidade física é calculada como uma convolução de com uma função de ponderação, onde denota os vizinhos da partícula : aqueles que estão localizados dentro de seu núcleo. A convolução é aproximada como um somatório de cada vizinho.${\ displaystyle i}$${\ displaystyle A_ {i}}$${\ displaystyle A_ {j}}$${\ displaystyle j}$${\ displaystyle i}$

Veja também

Notas

Referências

Leitura adicional

• Bracewell, R. (1986), The Fourier Transform and Its Applications (2ª ed.), McGraw-Hill, ISBN 0-07-116043-4.
• Damelin, S .; Miller, W. (2011), The Mathematics of Signal Processing , Cambridge University Press, ISBN 978-1107601048
• Diggle, PJ (1985), "A kernel method for smoothing point process data", Journal of the Royal Statistical Society, Series C , 34 (2): 138-147, doi : 10.2307 / 2347366 , JSTOR  2347366 , S2CID  116746157
• Dominguez-Torres, Alejandro (2 de novembro de 2010). “Origem e história da convolução”. 41 pgs. http://www.slideshare.net/Alexdfar/origin-adn-history-of-convolution . Cranfield, Bedford MK43 OAL, Reino Unido. Recuperado em 13 de março de 2013.
• Ghasemi, S. Hooman; Nowak, Andrzej S. (2017), "Reliability Index for Non-normal Distributions of Limit State Functions", Structural Engineering and Mechanics , 62 (3): 365-372, doi : 10.12989 / sem.2017.62.3.365
• Grinshpan, AZ (2017), "Uma inequação para várias convoluções com respeito à medida de probabilidade de Dirichlet", Advances in Applied Mathematics , 82 (1): 102–119, doi : 10.1016 / j.aam.2016.08.001
• Hewitt, Edwin; Ross, Kenneth A. (1979), Abstract harmonic analysis. Vol. I , Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Sciences], 115 (2ª ed.), Berlin, New York: Springer-Verlag , ISBN 978-3-540-09434-0, MR  0551496.
• Hewitt, Edwin; Ross, Kenneth A. (1970), Abstract harmonic analysis. Vol. II: Estrutura e análise para grupos compactos. Análise em grupos Abelianos localmente compactos , Die Grundlehren der mathematischen Wissenschaften, Band 152, Berlim, Nova York: Springer-Verlag , MR  0262773.
• Hörmander, L. (1983), A análise de operadores diferenciais parciais lineares I , Grundl. Matemática. Wissenschaft., 256 , Springer, doi : 10.1007 / 978-3-642-96750-4 , ISBN 3-540-12104-8, MR  0717035.
• Kassel, Christian (1995), Quantum groups , Graduate Texts in Mathematics, 155 , Berlin, New York: Springer-Verlag , doi : 10.1007 / 978-1-4612-0783-2 , ISBN 978-0-387-94370-1, MR  1321145.
• Knuth, Donald (1997), Seminumerical Algorithms (3rd. Ed.), Reading, Massachusetts: Addison – Wesley, ISBN 0-201-89684-2.
• Narici, Lawrence ; Beckenstein, Edward (2011). Espaços vetoriais topológicos . Matemática pura e aplicada (segunda edição). Boca Raton, FL: CRC Press. ISBN 978-1584888666. OCLC  144216834 .
• Reed, Michael; Simon, Barry (1975), Métodos de física matemática moderna. II. Análise de Fourier, auto-junção , New York-London: Academic Press Harcourt Brace Jovanovich, Publishers, pp. Xv + 361, ISBN 0-12-585002-6, MR  0493420
• Rudin, Walter (1962), Fourier analysis on groups , Interscience Tracts in Pure and Applied Mathematics, 12 , New York – London: Interscience Publishers, ISBN 0-471-52364-X, MR  0152834.
• Schaefer, Helmut H .; Wolff, Manfred P. (1999). Espaços vetoriais topológicos . GTM . 8 (segunda edição). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC  840278135 .
• Stein, Elias ; Weiss, Guido (1971), Introdução à Análise de Fourier em Espaços Euclidianos , Princeton University Press, ISBN 0-691-08078-X.
• Sobolev, VI (2001) [1994], "Convolution of functions" , Encyclopedia of Mathematics , EMS Press.
• Strichartz, R. (1994), A Guide to Distribution Theory and Fourier Transforms , CRC Press, ISBN 0-8493-8273-4.
• Titchmarsh, E (1948), Introdução à teoria das integrais de Fourier (2ª ed.), New York, NY: Chelsea Pub. Co. (publicado em 1986), ISBN 978-0-8284-0324-5.
• Trèves, François (2006) [1967]. Espaços Vetoriais Topológicos, Distribuições e Kernels . Mineola, NY: Dover Publications. ISBN 978-0-486-45352-1. OCLC  853623322 .
• Uludag, AM (1998), "Sobre a possível deterioração da suavidade sob a operação de convolução", J. Math. Anal. Appl. , 227 (2): 335-358, doi : 10.1006 / jmaa.1998.6091
• von zur Gathen, J .; Gerhard, J. (2003), Modern Computer Algebra , Cambridge University Press, ISBN 0-521-82646-2.

links externos

• Usos mais antigos: A entrada em Convolução contém algumas informações históricas.
• Convolução , no Briefbook de Análise de Dados
• http://www.jhu.edu/~signals/convolve/index.html Visual convolution Java Applet
• http://www.jhu.edu/~signals/discreteconv2/index.html Visual convolution Java Applet para funções de tempo discreto
• https://get-the-solution.net/projects/discret-convolution calculadora online discret-convolution
• https://lpsa.swarthmore.edu/Convolution/CI.html Demonstração de convolução e visualização em javascript
• https://phiresky.github.io/convolution-demo/ Outra demonstração de convolução em javascript
• Aulas sobre Processamento de Imagens: Uma coleção de 18 aulas em formato pdf da Vanderbilt University. A aula 7 é sobre convolução 2-D. , por Alan Peters
• * https://archive.org/details/Lectures_on_Image_Processing
• Tutorial interativo da operação da máscara do kernel de convolução
• Convolução em MathWorld
• Processador de resposta ao impulso Freeverb3 : processador de resposta ao impulso de latência zero de código aberto com plug-ins VST
• Demonstração em Flash interativo CS 178 da Stanford University mostrando como funciona a convolução espacial.
• Uma vídeo-aula sobre o assunto da convolução ministrada por Salman Khan
• Exemplo de convolução FFT para reconhecimento de padrão (processamento de imagem)
• Guia intuitivo para convolução Uma postagem de blog sobre uma interpretação intuitiva da convolução.