Produto cruzado - Cross product

Em matemática , o produto vetorial ou produto vetorial (ocasionalmente produto de área direcionado , para enfatizar seu significado geométrico) é uma operação binária em dois vetores no espaço tridimensional e é denotado pelo símbolo . Dados dois vectores linearmente independentes um e b , o produto cruzado, um × b (ler "b uma cruz"), é um vector que é perpendicular a ambos um e b , e assim o normal ao plano que os cont. Ele tem muitas aplicações em matemática, física , engenharia e programação de computadores . Não deve ser confundido com o produto escalar (produto de projeção). ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle \ times}$

Se dois vetores têm a mesma direção ou direção oposta exata um do outro (ou seja, eles não são linearmente independentes), ou se qualquer um deles tem comprimento zero, então seu produto vetorial é zero. Mais geralmente, a magnitude do produto é igual à área de um paralelogramo com os vetores dos lados; em particular, a magnitude do produto de dois vetores perpendiculares é o produto de seus comprimentos.

O produto vetorial é anticommutativo (ou seja, a × b = - b × a ) e é distributivo sobre a adição (ou seja, a × ( b + c ) = a × b + a × c ). O espaço junto com o produto vetorial é uma álgebra sobre os números reais , que não é comutativa nem associativa , mas é uma álgebra de Lie com o produto vetorial sendo o colchete de Lie . ${\ displaystyle \ mathbb {R} ^ {3}}$

Como o produto escalar, depende da métrica do espaço euclidiano , mas, ao contrário do produto escalar, também depende de uma escolha de orientação ou " lateralidade ". O produto pode ser generalizado de várias maneiras; pode ser feito independente da orientação, alterando o resultado para um pseudovetor , ou o produto exterior dos vetores pode ser usado em dimensões arbitrárias com um resultado bivetor ou de 2 formas . Além disso, usando a orientação e a estrutura métrica como para o produto vetorial tridimensional tradicional, pode-se, em n dimensões, tomar o produto de n - 1 vetores para produzir um vetor perpendicular a todos eles. Mas se o produto for limitado a produtos binários não triviais com resultados vetoriais, ele existe apenas em três e sete dimensões . (Veja § Generalizações , abaixo, para outras dimensões.)

Definição

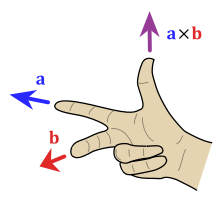
O produto cruzado de dois vectores de um e b é definido apenas no espaço tridimensional e é denotado por um × b . Em física e matemática aplicada , a notação de cunha a ∧ b é freqüentemente usada (em conjunto com o nome produto vetorial ), embora em matemática pura tal notação seja normalmente reservada apenas para o produto exterior, uma abstração do produto vetorial para n dimensões.

O produto cruzado um × b é definido como um vector c que é perpendicular (ortogonal) para ambos um e b , com uma direcção determinada pela regra da mão direita e uma amplitude igual à área do paralelogramo que os vectores abrangem.

O produto vetorial é definido pela fórmula

${\ displaystyle \ mathbf {a} \ times \ mathbf {b} = \ left \ | \ mathbf {a} \ right \ | \ left \ | \ mathbf {b} \ right \ | \ sin (\ theta) \ \ mathbf {n}}$

Onde:

• θ é o ângulo entre a e b no plano que os contém (portanto, está entre 0 ° e 180 °)
• ‖ Um ‖ e ‖ b ‖ são as magnitudes dos vectores de um e b
• e n é um vector unitário perpendicular ao plano que contém um e b , na direcção dada pela regra da mão direita (na figura).

Se os vectores a e b são paralelo (isto é, o ângulo θ entre eles é ou 0 ° ou 180 °), pela fórmula acima, o produto passe de um e b é o vector de zero 0 .

Direção

Por convenção, a direcção do vector n é dado pela regra da mão direita, onde um aponta simplesmente o dedo indicador da mão direita no sentido de um e o dedo médio na direcção de b . Então, o vetor n está saindo do polegar (veja a imagem ao lado). Usar esta regra implica que o produto vetorial é anticomutativo ; isto é, b × a = - ( a × b ) . Ao apontar o dedo indicador para b primeiro e, em seguida, apontar o dedo médio para a , o polegar será forçado na direção oposta, invertendo o sinal do vetor produto.

Como o operador de produto vetorial depende da orientação do espaço (conforme explícito na definição acima), o produto vetorial de dois vetores não é um vetor "verdadeiro", mas um pseudovetor . Consulte § Manuseio para obter mais detalhes.

Nomes

Em 1881, Josiah Willard Gibbs , e independentemente Oliver Heaviside , introduziram o produto escalar e o produto vetorial usando um ponto ( a . B ) e um "x" ( a x b ), respectivamente, para denotá-los.

Em 1877, para enfatizar o fato de que o resultado de um produto escalar é um escalar, enquanto o resultado de um produto vetorial é um vetor , William Kingdon Clifford cunhou os nomes alternativos de produto escalar e produto vetorial para as duas operações. Esses nomes alternativos ainda são amplamente usados ​​na literatura.

Tanto a notação cruzada ( a × b ) quanto o produto vetorial nome foram possivelmente inspirados no fato de que cada componente escalar de a × b é calculado multiplicando os componentes não correspondentes de a e b . Por outro lado, um produto escalar a ⋅ b envolve multiplicações entre os componentes correspondentes de a e b . Conforme explicado abaixo , o produto vetorial pode ser expresso na forma de um determinante de uma matriz 3 × 3 especial . De acordo com a regra de Sarrus , isso envolve multiplicações entre os elementos da matriz identificados por diagonais cruzadas.

Informática

Notação de coordenada

Os vetores de base padrão i , j e k satisfazem as seguintes igualdades em um sistema de coordenadas à direita :

${\ displaystyle {\ begin {alignat} {2} \ mathbf {\ color {blue} {i}} & \ times \ mathbf {\ color {red} {j}} && = \ mathbf {\ color {green} { k}} \\\ mathbf {\ color {red} {j}} & \ times \ mathbf {\ color {green} {k}} && = \ mathbf {\ color {blue} {i}} \\\ mathbf {\ color {green} {k}} & \ times \ mathbf {\ color {blue} {i}} && = \ mathbf {\ color {red} {j}} \ end {alinhados}}}$

que implicam, pela anticomutatividade do produto vetorial, que

${\ displaystyle {\ begin {alignat} {2} \ mathbf {\ color {red} {j}} & \ times \ mathbf {\ color {blue} {i}} && = - \ mathbf {\ color {green} {k}} \\\ mathbf {\ color {green} {k}} & \ times \ mathbf {\ color {red} {j}} && = - \ mathbf {\ color {blue} {i}} \\ \ mathbf {\ color {blue} {i}} & \ times \ mathbf {\ color {green} {k}} && = - \ mathbf {\ color {red} {j}} \ end {alignat}}}$

A anticomutatividade do produto vetorial (e a óbvia falta de independência linear) também implica que

${\ displaystyle \ mathbf {\ color {blue} {i}} \ times \ mathbf {\ color {blue} {i}} = \ mathbf {\ color {red} {j}} \ times \ mathbf {\ color { red} {j}} = \ mathbf {\ color {green} {k}} \ times \ mathbf {\ color {green} {k}} = \ mathbf {0}}$(o vetor zero ).

Essas igualdades, junto com a distributividade e linearidade do produto vetorial (embora nenhuma delas decorra facilmente da definição dada acima), são suficientes para determinar o produto vetorial de quaisquer dois vetores a e b . Cada vetor pode ser definido como a soma de três componentes ortogonais paralelos aos vetores de base padrão:

${\ displaystyle {\ begin {alignat} {3} \ mathbf {a} & = a_ {1} \ mathbf {\ color {blue} {i}} && + a_ {2} \ mathbf {\ color {red} { j}} && + a_ {3} \ mathbf {\ color {green} {k}} \\\ mathbf {b} & = b_ {1} \ mathbf {\ color {blue} {i}} && + b_ { 2} \ mathbf {\ color {red} {j}} && + b_ {3} \ mathbf {\ color {green} {k}} \ end {alignat}}}$

Seu produto vetorial a × b pode ser expandido usando distributividade:

${\ displaystyle {\ begin {align} \ mathbf {a} \ times \ mathbf {b} = {} & (a_ {1} \ mathbf {\ color {blue} {i}} + a_ {2} \ mathbf { \ color {red} {j}} + a_ {3} \ mathbf {\ color {green} {k}}) \ times (b_ {1} \ mathbf {\ color {blue} {i}} + b_ {2 } \ mathbf {\ color {red} {j}} + b_ {3} \ mathbf {\ color {green} {k}}) \\ = {} & a_ {1} b_ {1} (\ mathbf {\ color {blue} {i}} \ times \ mathbf {\ color {blue} {i}}) + a_ {1} b_ {2} (\ mathbf {\ color {blue} {i}} \ times \ mathbf {\ color {red} {j}}) + a_ {1} b_ {3} (\ mathbf {\ color {blue} {i}} \ times \ mathbf {\ color {green} {k}}) + {} \ \ & a_ {2} b_ {1} (\ mathbf {\ color {red} {j}} \ times \ mathbf {\ color {blue} {i}}) + a_ {2} b_ {2} (\ mathbf { \ color {red} {j}} \ times \ mathbf {\ color {red} {j}}) + a_ {2} b_ {3} (\ mathbf {\ color {red} {j}} \ times \ mathbf {\ color {green} {k}}) + {} \\ & a_ {3} b_ {1} (\ mathbf {\ color {green} {k}} \ times \ mathbf {\ color {blue} {i} }) + a_ {3} b_ {2} (\ mathbf {\ color {green} {k}} \ times \ mathbf {\ color {red} {j}}) + a_ {3} b_ {3} (\ mathbf {\ color {green} {k}} \ times \ mathbf {\ color {green} {k}}) \\\ end {alinhado}}}$

Isso pode ser interpretado como a decomposição de a × b na soma de nove produtos cruzados mais simples envolvendo vetores alinhados com i , j ou k . Cada um desses nove produtos cruzados opera em dois vetores fáceis de manusear, pois são paralelos ou ortogonais entre si. A partir dessa decomposição, usando as igualdades mencionadas acima e coletando termos semelhantes, obtemos:

${\ displaystyle {\ begin {align} \ mathbf {a} \ times \ mathbf {b} = {} & \ quad \ a_ {1} b_ {1} \ mathbf {0} + a_ {1} b_ {2} \ mathbf {\ color {green} {k}} -a_ {1} b_ {3} \ mathbf {\ color {red} {j}} \\ & - a_ {2} b_ {1} \ mathbf {\ color {verde} {k}} + a_ {2} b_ {2} \ mathbf {0} + a_ {2} b_ {3} \ mathbf {\ color {blue} {i}} \\ & + a_ {3} b_ {1} \ mathbf {\ color {red} {j}} \ -a_ {3} b_ {2} \ mathbf {\ color {blue} {i}} \ + a_ {3} b_ {3} \ mathbf {0} \\ = {} & (a_ {2} b_ {3} -a_ {3} b_ {2}) \ mathbf {\ color {blue} {i}} + (a_ {3} b_ {1} -a_ {1} b_ {3}) \ mathbf {\ color {red} {j}} + (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {\ color {green} {k}} \\\ end {alinhado}}}$

o que significa que os três componentes escalares do vetor resultante s = s ₁ i + s ₂ j + s ₃ k = a × b são

${\ displaystyle {\ begin {align} s_ {1} & = a_ {2} b_ {3} -a_ {3} b_ {2} \\ s_ {2} & = a_ {3} b_ {1} -a_ {1} b_ {3} \\ s_ {3} & = a_ {1} b_ {2} -a_ {2} b_ {1} \ end {alinhado}}}$

Usando vetores de coluna , podemos representar o mesmo resultado da seguinte maneira:

${\ displaystyle {\ begin {pmatrix} s_ {1} \\ s_ {2} \\ s_ {3} \ end {pmatrix}} = {\ begin {pmatrix} a_ {2} b_ {3} -a_ {3 } b_ {2} \\ a_ {3} b_ {1} -a_ {1} b_ {3} \\ a_ {1} b_ {2} -a_ {2} b_ {1} \ end {pmatriz}}}$

Notação de matriz

O produto vetorial também pode ser expresso como o determinante formal :

${\ displaystyle \ mathbf {a \ times b} = {\ begin {vmatrix} \ mathbf {i} & \ mathbf {j} & \ mathbf {k} \\ a_ {1} & a_ {2} & a_ {3} \ \ b_ {1} & b_ {2} & b_ {3} \\\ end {vmatrix}}}$

Este determinante pode ser calculado usando a regra de Sarrus ou a expansão do cofator . Usando a regra de Sarrus, ele se expande para

${\ displaystyle {\ begin {alinhados} \ mathbf {a \ times b} & = (a_ {2} b_ {3} \ mathbf {i} + a_ {3} b_ {1} \ mathbf {j} + a_ { 1} b_ {2} \ mathbf {k}) - (a_ {3} b_ {2} \ mathbf {i} + a_ {1} b_ {3} \ mathbf {j} + a_ {2} b_ {1} \ mathbf {k}) \\ & = (a_ {2} b_ {3} -a_ {3} b_ {2}) \ mathbf {i} + (a_ {3} b_ {1} -a_ {1} b_ {3}) \ mathbf {j} + (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {k}. \ End {alinhado}}}$

Usando a expansão de cofator ao longo da primeira linha, em vez disso, ele se expande para

${\ displaystyle {\ begin {align} \ mathbf {a \ times b} & = {\ begin {vmatrix} a_ {2} & a_ {3} \\ b_ {2} & b_ {3} \ end {vmatrix}} \ mathbf {i} - {\ begin {vmatrix} a_ {1} & a_ {3} \\ b_ {1} & b_ {3} \ end {vmatrix}} \ mathbf {j} + {\ begin {vmatrix} a_ {1 } & a_ {2} \\ b_ {1} & b_ {2} \ end {vmatrix}} \ mathbf {k} \\ & = (a_ {2} b_ {3} -a_ {3} b_ {2}) \ mathbf {i} - (a_ {1} b_ {3} -a_ {3} b_ {1}) \ mathbf {j} + (a_ {1} b_ {2} -a_ {2} b_ {1}) \ mathbf {k}, \ end {alinhado}}}$

que fornece os componentes do vetor resultante diretamente.

Usando tensores Levi-Civita

• Em qualquer base, o produto vetorial é dado pela fórmula tensorial onde é o tensor covariante de Levi-Civita (notamos a posição dos índices). Isso corresponde à fórmula intrínseca dada aqui .${\ displaystyle a \ times b}$${\ displaystyle E_ {ijk} a ^ {i} b ^ {j}}$${\ displaystyle E_ {ijk}}$
• Numa base ortonormal tendo a mesma orientação que o espaço , é dada pela fórmula pseudotensorial onde está o símbolo de Levi-Civita (que é um pseudotensor). Essa é a fórmula usada para a física cotidiana, mas só funciona neste caso especial de base.${\ displaystyle a \ times b}$${\ displaystyle \ varepsilon _ {ijk} a ^ {i} b ^ {j}}$${\ displaystyle \ varepsilon _ {ijk}}$
• Em qualquer base ortonormal, é dada pela fórmula pseudo-tensorial onde indica se a base tem a mesma orientação do espaço ou não.${\ displaystyle a \ times b}$${\ displaystyle (-1) ^ {B} \ varepsilon _ {ijk} a ^ {i} b ^ {j}}$${\ displaystyle (-1) ^ {B} = \ pm 1}$

A última fórmula evita ter que mudar a orientação do espaço quando invertemos uma base ortonormal.

Propriedades

Significado geométrico

A magnitude do produto cruzado pode ser interpretado como positivo a área do paralelogramo que tem um e b , como os lados (ver Figura 1):

${\ displaystyle \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | = \ left \ | \ mathbf {a} \ right \ | \ left \ | \ mathbf {b} \ right \ | | \ sin \ theta |.}$

Na verdade, também se pode calcular o volume V de um paralelepípedo com uma , b e c como arestas, utilizando uma combinação de um produto de cruzamento e um produto escalar, chamou produto escalar triplo (ver Figura 2):

${\ displaystyle \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) = \ mathbf {b} \ cdot (\ mathbf {c} \ times \ mathbf {a}) = \ mathbf { c} \ cdot (\ mathbf {a} \ times \ mathbf {b}).}$

Como o resultado do triplo produto escalar pode ser negativo, o volume do paralelepípedo é dado pelo seu valor absoluto. Por exemplo,

${\ displaystyle V = | \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) |.}$

Como a magnitude do produto vetorial varia pelo seno do ângulo entre seus argumentos, o produto vetorial pode ser pensado como uma medida de perpendicularidade da mesma forma que o produto escalar é uma medida de paralelismo . Dados dois vetores unitários , seu produto vetorial tem uma magnitude de 1 se os dois forem perpendiculares e uma magnitude de zero se os dois forem paralelos. O produto escalar de dois vetores unitários se comporta de maneira oposta: é zero quando os vetores unitários são perpendiculares e 1 se os vetores unitários são paralelos.

Os vetores unitários permitem duas identidades convenientes: o produto escalar de dois vetores unitários produz o cosseno (que pode ser positivo ou negativo) do ângulo entre os dois vetores unitários. A magnitude do produto vetorial dos dois vetores unitários produz o seno (que sempre será positivo).

Propriedades algébricas

Se o produto vetorial de dois vetores é o vetor zero (ou seja, a × b = 0 ), então uma ou ambas as entradas são o vetor zero, ( a = 0 ou b = 0 ) ou então eles são paralelos ou antiparalelo ( a ∥ b ) de forma que o seno do ângulo entre eles seja zero ( θ = 0 ° ou θ = 180 ° e sen  θ = 0 ).

O produto cruzado próprio de um vetor é o vetor zero:

${\ displaystyle \ mathbf {a} \ times \ mathbf {a} = \ mathbf {0}.}$

O produto vetorial é anticomutativo ,

${\ displaystyle \ mathbf {a} \ times \ mathbf {b} = - (\ mathbf {b} \ times \ mathbf {a}),}$

distributiva sobre adição,

${\ displaystyle \ mathbf {a} \ times (\ mathbf {b} + \ mathbf {c}) = (\ mathbf {a} \ times \ mathbf {b}) + (\ mathbf {a} \ times \ mathbf { c}),}$

e compatível com multiplicação escalar para que

${\ displaystyle (r \, \ mathbf {a}) \ times \ mathbf {b} = \ mathbf {a} \ times (r \, \ mathbf {b}) = r \, (\ mathbf {a} \ times \ mathbf {b}).}$

Não é associativo , mas satisfaz a identidade Jacobi :

${\ displaystyle \ mathbf {a} \ times (\ mathbf {b} \ times \ mathbf {c}) + \ mathbf {b} \ times (\ mathbf {c} \ times \ mathbf {a}) + \ mathbf { c} \ times (\ mathbf {a} \ times \ mathbf {b}) = \ mathbf {0}.}$

Distributividade, linearidade e identidade de Jacobi mostram que o espaço vetorial R ³ junto com a adição de vetores e o produto vetorial formam uma álgebra de Lie , a álgebra de Lie do grupo ortogonal real em 3 dimensões, SO (3) . O produto vetorial não obedece à lei de cancelamento ; ou seja, a × b = a × c com a ≠ 0 não implica b = c , mas apenas que:

${\ displaystyle {\ begin {alinhados} \ mathbf {0} & = (\ mathbf {a} \ times \ mathbf {b}) - (\ mathbf {a} \ times \ mathbf {c}) \\ & = \ mathbf {a} \ times (\ mathbf {b} - \ mathbf {c}). \\\ end {alinhado}}}$

Este pode ser o caso onde b e c cancelam, mas adicionalmente onde a e b - c são paralelos; ou seja, eles estão relacionados por um fator de escala t , levando a:

${\ displaystyle \ mathbf {c} = \ mathbf {b} + t \, \ mathbf {a},}$

para algum escalar t .

Se, em adição a um × b = um × c e um ≠ 0 como acima, que é o caso que uma ⋅ b = um ⋅ c então

${\ displaystyle {\ begin {alinhados} \ mathbf {a} \ times (\ mathbf {b} - \ mathbf {c}) & = \ mathbf {0} \\\ mathbf {a} \ cdot (\ mathbf {b } - \ mathbf {c}) & = 0, \ end {alinhado}}}$

Como b - c não podem ser paralelas simultaneamente (para o produto cruzado a ser 0 ) e perpendicular (para o produto de pontos para ser 0) para um , que deve ser o caso em que b e c cancelar: b = c .

Pela definição geométrica, o produto vetorial é invariante sob rotações adequadas em torno do eixo definido por a × b . Em fórmulas:

${\ displaystyle (R \ mathbf {a}) \ times (R \ mathbf {b}) = R (\ mathbf {a} \ times \ mathbf {b})}$, onde é uma matriz de rotação com .${\ displaystyle R}$${\ displaystyle \ det (R) = 1}$

De forma mais geral, o produto cruzado obedece à seguinte identidade em transformações de matriz :

${\ displaystyle (M \ mathbf {a}) \ times (M \ mathbf {b}) = (\ det M) \ left (M ^ {- 1} \ right) ^ {\ mathrm {T}} (\ mathbf {a} \ times \ mathbf {b}) = \ operatorname {cof} M (\ mathbf {a} \ times \ mathbf {b})}$

onde é uma matriz 3 por 3 e é a transposta do inverso e é a matriz cofator. Pode-se ver prontamente como esta fórmula se reduz à anterior se for uma matriz de rotação. ${\ displaystyle M}$${\ displaystyle \ left (M ^ {- 1} \ right) ^ {\ mathrm {T}}}$${\ displaystyle \ operatorname {cof}}$${\ displaystyle M}$

O produto vetorial de dois vetores encontra-se no espaço nulo da matriz 2 × 3 com os vetores como linhas:

${\ displaystyle \ mathbf {a} \ times \ mathbf {b} \ in NS \ left ({\ begin {bmatrix} \ mathbf {a} \\\ mathbf {b} \ end {bmatrix}} \ right).}$

Para a soma de dois produtos cruzados, a seguinte identidade é válida:

${\ displaystyle \ mathbf {a} \ times \ mathbf {b} + \ mathbf {c} \ times \ mathbf {d} = (\ mathbf {a} - \ mathbf {c}) \ times (\ mathbf {b} - \ mathbf {d}) + \ mathbf {a} \ times \ mathbf {d} + \ mathbf {c} \ times \ mathbf {b}.}$

Diferenciação

A regra do produto do cálculo diferencial se aplica a qualquer operação bilinear e, portanto, também ao produto vetorial:

${\ displaystyle {\ frac {d} {dt}} (\ mathbf {a} \ times \ mathbf {b}) = {\ frac {d \ mathbf {a}} {dt}} \ times \ mathbf {b} + \ mathbf {a} \ times {\ frac {d \ mathbf {b}} {dt}},}$

onde a e b são vetores que dependem da variável real t .

Expansão tripla do produto

O produto vetorial é usado em ambas as formas do produto triplo. O produto triplo escalar de três vetores é definido como

${\ displaystyle \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}),}$

É o volume assinada do paralelepípedo com arestas um , b e c e, como tal, os vectores podem ser utilizados em qualquer ordem que é uma permutação mesmo da ordenação acima. Portanto, os seguintes são iguais:

${\ displaystyle \ mathbf {a} \ cdot (\ mathbf {b} \ times \ mathbf {c}) = \ mathbf {b} \ cdot (\ mathbf {c} \ times \ mathbf {a}) = \ mathbf { c} \ cdot (\ mathbf {a} \ times \ mathbf {b}),}$

O produto vetorial triplo é o produto vetorial de um vetor com o resultado de outro produto vetorial e está relacionado ao produto escalar pela seguinte fórmula

${\ displaystyle \ mathbf {a} \ times (\ mathbf {b} \ times \ mathbf {c}) = \ mathbf {b} (\ mathbf {a} \ cdot \ mathbf {c}) - \ mathbf {c} (\ mathbf {a} \ cdot \ mathbf {b}).}$

O mnemônico "BAC menos CAB" é usado para lembrar a ordem dos vetores no membro da mão direita. Esta fórmula é usada em física para simplificar os cálculos de vetores. Um caso especial, em relação aos gradientes e útil no cálculo vetorial , é

${\ displaystyle {\ begin {alinhado} \ nabla \ times (\ nabla \ times \ mathbf {f}) & = \ nabla (\ nabla \ cdot \ mathbf {f}) - (\ nabla \ cdot \ nabla) \ mathbf {f} \\ & = \ nabla (\ nabla \ cdot \ mathbf {f}) - \ nabla ^ {2} \ mathbf {f}, \\\ end {alinhado}}}$

onde ∇ ² é o operador vetorial Laplaciano .

Outras identidades relacionam o produto vetorial ao produto escalar triplo:

${\ displaystyle {\ begin {align} (\ mathbf {a} \ times \ mathbf {b}) \ times (\ mathbf {a} \ times \ mathbf {c}) & = (\ mathbf {a} \ cdot ( \ mathbf {b} \ times \ mathbf {c})) \ mathbf {a} \\ (\ mathbf {a} \ times \ mathbf {b}) \ cdot (\ mathbf {c} \ times \ mathbf {d} ) & = \ mathbf {b} ^ {\ mathrm {T}} \ left (\ left (\ mathbf {c} ^ {\ mathrm {T}} \ mathbf {a} \ right) I- \ mathbf {c} \ mathbf {a} ^ {\ mathrm {T}} \ right) \ mathbf {d} \\ & = (\ mathbf {a} \ cdot \ mathbf {c}) (\ mathbf {b} \ cdot \ mathbf { d}) - (\ mathbf {a} \ cdot \ mathbf {d}) (\ mathbf {b} \ cdot \ mathbf {c}) \ end {alinhado}}}$

onde I é a matriz de identidade.

Formulação alternativa

O produto vetorial e o produto escalar são relacionados por:

${\ displaystyle \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | ^ {2} = \ left \ | \ mathbf {a} \ right \ | ^ {2} \ left \ | \ mathbf {b} \ right \ | ^ {2} - (\ mathbf {a} \ cdot \ mathbf {b}) ^ {2}.}$

O lado direito é o determinante de Gram de um e b , o quadrado da área do paralelogramo definido pelos vectores. Essa condição determina a magnitude do produto vetorial. A saber, uma vez que o produto escalar é definido, em termos do ângulo θ entre os dois vetores, como:

${\ displaystyle \ mathbf {a \ cdot b} = \ left \ | \ mathbf {a} \ right \ | \ left \ | \ mathbf {b} \ right \ | \ cos \ theta,}$

a relação fornecida acima pode ser reescrita da seguinte forma:

${\ displaystyle \ left \ | \ mathbf {a \ times b} \ right \ | ^ {2} = \ left \ | \ mathbf {a} \ right \ | ^ {2} \ left \ | \ mathbf {b} \ right \ | ^ {2} \ left (1- \ cos ^ {2} \ theta \ right).}$

Invocando a identidade trigonométrica pitagórica, obtém-se:

${\ displaystyle \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | = \ left \ | \ mathbf {a} \ right \ | \ left \ | \ mathbf {b} \ right \ | \ left | \ sin \ theta \ right |,}$

que representa a magnitude do produto cruzado expressa em termos de θ , igual à área do paralelogramo definido por um e b (ver definição acima).

A combinação deste requisito e a propriedade de que o produto passe ser ortogonal para os seus constituintes a e b fornece uma definição alternativa do produto cruzado.

A identidade de Lagrange

A relação:

${\ displaystyle \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | ^ {2} \ equiv \ det {\ begin {bmatrix} \ mathbf {a} \ cdot \ mathbf {a} & \ mathbf {a} \ cdot \ mathbf {b} \\\ mathbf {a} \ cdot \ mathbf {b} & \ mathbf {b} \ cdot \ mathbf {b} \\\ end {bmatrix}} \ equiv \ esquerda \ | \ mathbf {a} \ direita \ | ^ {2} \ esquerda \ | \ mathbf {b} \ direita \ | ^ {2} - (\ mathbf {a} \ cdot \ mathbf {b}) ^ { 2}.}$

pode ser comparada com outra relação envolvendo o lado direito, a saber, a identidade de Lagrange expressa como:

${\ displaystyle \ sum _ {1 \ leq i <j \ leq n} \ left (a_ {i} b_ {j} -a_ {j} b_ {i} \ right) ^ {2} \ equiv \ left \ | \ mathbf {a} \ right \ | ^ {2} \ left \ | \ mathbf {b} \ right \ | ^ {2} - (\ mathbf {a \ cdot b}) ^ {2} \,}$

onde a e b podem ser vetores n- dimensionais. Isso também mostra que a forma de volume Riemanniana para superfícies é exatamente o elemento de superfície do cálculo vetorial. No caso em que n = 3 , a combinação dessas duas equações resulta na expressão para a magnitude do produto vetorial em termos de seus componentes:

${\ displaystyle {\ begin {alinhado} & \ left \ | \ mathbf {a} \ times \ mathbf {b} \ right \ | ^ {2} \ equiv \ sum _ {1 \ leq i <j \ leq 3} \ left (a_ {i} b_ {j} -a_ {j} b_ {i} \ right) ^ {2} \\\ equiv {} & \ left (a_ {1} b_ {2} -b_ {1} a_ {2} \ direita) ^ {2} + \ esquerda (a_ {2} b_ {3} -a_ {3} b_ {2} \ direita) ^ {2} + \ esquerda (a_ {3} b_ {1 } -a_ {1} b_ {3} \ direita) ^ {2} \. \ end {alinhado}}}$

O mesmo resultado é encontrado diretamente usando os componentes do produto vetorial encontrados em:

${\ displaystyle \ mathbf {a} \ times \ mathbf {b} \ equiv \ det {\ begin {bmatrix} {\ hat {\ mathbf {i}}} & {\ hat {\ mathbf {j}}} & { \ hat {\ mathbf {k}}} \\ a_ {1} & a_ {2} & a_ {3} \\ b_ {1} & b_ {2} & b_ {3} \\\ end {bmatrix}}.}$

Em R ³ , a equação de Lagrange é um caso especial da multiplicatividade | vw | = | v || w | da norma na álgebra de quaternion .

É um caso especial de outra fórmula, também às vezes chamada de identidade de Lagrange, que é o caso tridimensional da identidade Binet-Cauchy :

${\ displaystyle (\ mathbf {a} \ times \ mathbf {b}) \ cdot (\ mathbf {c} \ times \ mathbf {d}) \ equiv (\ mathbf {a} \ cdot \ mathbf {c}) ( \ mathbf {b} \ cdot \ mathbf {d}) - (\ mathbf {a} \ cdot \ mathbf {d}) (\ mathbf {b} \ cdot \ mathbf {c}).}$

Se a = c e b = d, isso simplifica para a fórmula acima.

Geradores infinitesimais de rotações

O produto vetorial descreve convenientemente os geradores infinitesimais de rotações em R ³ . Especificamente, se n for um vetor unitário em R ³ e R ( φ ,  n ) denota uma rotação em torno do eixo através da origem especificada por n , com ângulo φ (medido em radianos, no sentido anti-horário quando visto a partir da ponta de n ), então

${\ displaystyle \ left. {d \ over d \ phi} \ right | _ {\ phi = 0} R (\ phi, {\ boldsymbol {n}}) {\ boldsymbol {x}} = {\ boldsymbol {n }} \ times {\ boldsymbol {x}}}$

para cada vetor x em R ³ . O produto vetorial com n, portanto, descreve o gerador infinitesimal das rotações em torno de n . Esses geradores infinitesimais formam a álgebra de Lie so (3) do grupo de rotação SO (3) , e obtemos o resultado que a álgebra de Lie R ³ com produto vetorial é isomórfica à álgebra de Lie so (3).

Formas alternativas de calcular

Conversão para multiplicação de matrizes

O produto vetorial vetorial também pode ser expresso como o produto de uma matriz assimétrica e um vetor:

${\ displaystyle {\ begin {alinhados} \ mathbf {a} \ times \ mathbf {b} = [\ mathbf {a}] _ {\ times} \ mathbf {b} & = {\ begin {bmatrix} \, 0 & \! - a_ {3} & \, \, a_ {2} \\\, \, a_ {3} & 0 & \! - a_ {1} \\ - a_ {2} & \, \, a_ {1} & \, 0 \ end {bmatrix}} {\ begin {bmatrix} b_ {1} \\ b_ {2} \\ b_ {3} \ end {bmatrix}} \\\ mathbf {a} \ times \ mathbf { b} = {[\ mathbf {b}] _ {\ times}} ^ {\ mathrm {\! \! T}} \ mathbf {a} & = {\ begin {bmatrix} \, 0 & \, \, b_ {3} & \! - b_ {2} \\ - b_ {3} & 0 & \, \, b_ {1} \\\, \, b_ {2} & \! - b_ {1} & \, 0 \ end {bmatrix}} {\ begin {bmatrix} a_ {1} \\ a_ {2} \\ a_ {3} \ end {bmatrix}}, \ end {alinhado}}}$

onde o sobrescrito ^T se refere à operação de transposição , e [ a ] _× é definido por:

${\ displaystyle [\ mathbf {a}] _ {\ times} {\ stackrel {\ rm {def}} {=}} {\ begin {bmatrix} \, \, 0 & \! - a_ {3} & \, \, \, a_ {2} \\\, \, \, a_ {3} & 0 & \! - a_ {1} \\\! - a_ {2} & \, \, a_ {1} & \, \ , 0 \ end {bmatrix}}.}$

As colunas [ a ] _{×, i} da matriz assimétrica para um vetor a também podem ser obtidas calculando o produto vetorial com vetores unitários . Isso é,

${\ displaystyle [\ mathbf {a}] _ {\ times, i} = \ mathbf {a} \ times \ mathbf {{\ hat {e}} _ {i}}, \; i \ in \ {1, 2,3 \}}$

ou

${\ displaystyle [\ mathbf {a}] _ {\ times} = \ sum _ {i = 1} ^ {3} \ left (\ mathbf {a} \ times \ mathbf {{\ hat {e}} _ { i}} \ right) \ otimes \ mathbf {{\ hat {e}} _ {i}},}$

onde está o operador de produto externo . ${\ displaystyle \ otimes}$

Além disso, se a for expresso como um produto vetorial:

${\ displaystyle \ mathbf {a} = \ mathbf {c} \ times \ mathbf {d}}$

então

${\ displaystyle [\ mathbf {a}] _ {\ times} = \ mathbf {d} \ mathbf {c} ^ {\ mathrm {T}} - \ mathbf {c} \ mathbf {d} ^ {\ mathrm { T}}.}$

Prova por substituição

A avaliação do produto vetorial dá ${\ displaystyle \ mathbf {a} = \ mathbf {c} \ times \ mathbf {d} = {\ begin {pmatrix} c_ {2} d_ {3} -c_ {3} d_ {2} \\ c_ {3 } d_ {1} -c_ {1} d_ {3} \\ c_ {1} d_ {2} -c_ {2} d_ {1} \ end {pmatrix}}}$ Portanto, o lado esquerdo é igual a ${\ displaystyle [\ mathbf {a}] _ {\ times} = {\ begin {bmatrix} 0 & c_ {2} d_ {1} -c_ {1} d_ {2} & c_ {3} d_ {1} -c_ { 1} d_ {3} \\ c_ {1} d_ {2} -c_ {2} d_ {1} & 0 & c_ {3} d_ {2} -c_ {2} d_ {3} \\ c_ {1} d_ { 3} -c_ {3} d_ {1} & c_ {2} d_ {3} -c_ {3} d_ {2} & 0 \ end {bmatrix}}}$ Agora, para o lado direito, ${\ displaystyle \ mathbf {c} \ mathbf {d} ^ {\ mathrm {T}} = {\ begin {bmatrix} c_ {1} d_ {1} & c_ {1} d_ {2} & c_ {1} d_ { 3} \\ c_ {2} d_ {1} & c_ {2} d_ {2} & c_ {2} d_ {3} \\ c_ {3} d_ {1} & c_ {3} d_ {2} & c_ {3} d_ {3} \ end {bmatrix}}}$ E sua transposição é ${\ displaystyle \ mathbf {d} \ mathbf {c} ^ {\ mathrm {T}} = {\ begin {bmatrix} c_ {1} d_ {1} & c_ {2} d_ {1} & c_ {3} d_ { 1} \\ c_ {1} d_ {2} & c_ {2} d_ {2} & c_ {3} d_ {2} \\ c_ {1} d_ {3} & c_ {2} d_ {3} & c_ {3} d_ {3} \ end {bmatrix}}}$ A avaliação do lado direito dá ${\ displaystyle \ mathbf {d} \ mathbf {c} ^ {\ mathrm {T}} - \ mathbf {c} \ mathbf {d} ^ {\ mathrm {T}} = {\ begin {bmatrix} 0 & c_ {2 } d_ {1} -c_ {1} d_ {2} & c_ {3} d_ {1} -c_ {1} d_ {3} \\ c_ {1} d_ {2} -c_ {2} d_ {1} & 0 & c_ {3} d_ {2} -c_ {2} d_ {3} \\ c_ {1} d_ {3} -c_ {3} d_ {1} & c_ {2} d_ {3} -c_ {3} d_ {2} & 0 \ end {bmatrix}}}$ A comparação mostra que o lado esquerdo é igual ao lado direito.

Este resultado pode ser generalizado para dimensões superiores usando álgebra geométrica . Em particular, em qualquer dimensão, os bivetores podem ser identificados com matrizes assimétricas, de modo que o produto entre uma matriz simétrica e um vetor é equivalente à parte de grau 1 do produto de um bivetor e vetor. Em três dimensões, os bivetores são duais aos vetores, de modo que o produto é equivalente ao produto vetorial, com o bivetor em vez de seu vetor dual. Em dimensões mais altas, o produto ainda pode ser calculado, mas os bivetores têm mais graus de liberdade e não são equivalentes aos vetores.

Freqüentemente, essa notação também é muito mais fácil de trabalhar, por exemplo, na geometria epipolar .

Das propriedades gerais do produto vetorial segue imediatamente que

${\ displaystyle [\ mathbf {a}] _ {\ times} \, \ mathbf {a} = \ mathbf {0}}$   e   ${\ displaystyle \ mathbf {a} ^ {\ mathrm {T}} \, [\ mathbf {a}] _ {\ times} = \ mathbf {0}}$

e do fato de que [ a ] _× é assimétrico-simétrico, segue-se que

${\ displaystyle \ mathbf {b} ^ {\ mathrm {T}} \, [\ mathbf {a}] _ {\ times} \, \ mathbf {b} = 0.}$

A expansão de produto triplo mencionada acima (regra bac – cab) pode ser facilmente comprovada usando esta notação.

Como mencionado acima, a álgebra de Lie R ³ com produto vetorial é isomórfica à álgebra de Lie so (3) , cujos elementos podem ser identificados com as matrizes simétricas 3 × 3. O mapa a → [ a ] _× fornece um isomorfismo entre R ³ e assim (3) . Sob este mapa, o produto vetorial de 3 vetores corresponde ao comutador de matrizes com simetria de inclinação 3x3.

Conversão de matriz para produto cruzado com vetores de base canônicos

Denotando com o -ésimo vetor de base canônica, o produto vetorial de um vetor genérico com é dado por:, onde ${\ displaystyle \ mathbf {e} _ {i} \ in \ mathbf {R} ^ {3 \ vezes 1}}$${\ displaystyle i}$${\ displaystyle \ mathbf {v} \ in \ mathbf {R} ^ {3 \ vezes 1}}$${\ displaystyle \ mathbf {e} _ {i}}$${\ displaystyle \ mathbf {v} \ times \ mathbf {e} _ {i} = \ mathbf {C} _ {i} \ mathbf {v}}$ ${\ displaystyle \ mathbf {C} _ {1} = {\ begin {bmatrix} 0 & 0 & 0 \\ 0 & 0 & 1 \\ 0 & -1 & 0 \ end {bmatrix}}, \ quad \ mathbf {C} _ {2} = {\ begin {bmatrix} 0 & 0 & -1 \\ 0 & 0 & 0 \\ 1 & 0 & 0 \ end {bmatrix}}, \ quad \ mathbf {C} _ {3} = {\ begin {bmatrix} 0 & 1 & 0 \\ - 1 & 0 & 0 \\ 0 & 0 & 0 \ end {bmatrix} }}$ Essas matrizes compartilham as seguintes propriedades: ${\ displaystyle \ mathbf {C} _ {i} ^ {\ textrm {T}} = - \ mathbf {C} _ {i}}$ (simétrico inclinado); Tanto o traço quanto o determinante são zero; ${\ displaystyle {\ text {rank}} (\ mathbf {C} _ {i}) = 2}$; ${\ displaystyle \ mathbf {C} _ {i} \ mathbf {C} _ {i} ^ {\ textrm {T}} = \ mathbf {P} _ {\ mathbf {e} _ {i}} ^ {^ {\ perp}}}$ (Veja abaixo); A matriz de projeção ortogonal de um vetor é dada por . A matriz de projeção no complemento ortogonal é dada por , onde está a matriz identidade. Para o caso especial de , pode-se verificar que ${\ displaystyle \ mathbf {v} \ neq \ mathbf {0}}$${\ displaystyle \ mathbf {P} _ {\ mathbf {v}} = \ mathbf {v} \ left (\ mathbf {v} ^ {\ textrm {T}} \ mathbf {v} \ right) ^ {- 1 } \ mathbf {v} ^ {T}}$${\ displaystyle \ mathbf {P} _ {\ mathbf {v}} ^ {^ {\ perp}} = \ mathbf {I} - \ mathbf {P} _ {\ mathbf {v}}}$${\ displaystyle \ mathbf {I}}$${\ displaystyle \ mathbf {v} = \ mathbf {e} _ {i}}$ ${\ displaystyle \ mathbf {P} _ {\ mathbf {e} _ {1}} ^ {^ {\ perp}} = {\ begin {bmatrix} 0 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}}, \ quad \ mathbf {P} _ {\ mathbf {e} _ {2}} ^ {^ {\ perp}} = {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 1 \ end {bmatrix}}, \ quad \ mathbf {P} _ {\ mathbf {e} _ {3}} ^ {^ {\ perp}} = {\ begin {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 0 \ end {bmatrix}}}$ Para outras propriedades de matrizes de projeção ortogonal, consulte projeção (álgebra linear) .

Notação de índice para tensores

O produto _vetorial pode, alternativamente, ser definido em termos do símbolo de Levi-Civita ε _ijk e um produto escalar η ^mi (= δ ^mi para uma base ortonormal), que são úteis na conversão de notação vetorial para aplicações de tensores:

${\ displaystyle \ mathbf {c} = \ mathbf {a \ times b} \ Leftrightarrow \ c ^ {m} = \ sum _ {i = 1} ^ {3} \ sum _ {j = 1} ^ {3} \ sum _ {k = 1} ^ {3} \ eta ^ {mi} \ varepsilon _ {ijk} a ^ {j} b ^ {k}}$

onde os índices correspondem aos componentes do vetor. Esta caracterização do produto vetorial é frequentemente expressa de forma mais compacta usando a convenção de soma de Einstein como ${\ displaystyle i, j, k}$

${\ displaystyle \ mathbf {c} = \ mathbf {a \ times b} \ Leftrightarrow \ c ^ {m} = \ eta ^ {mi} \ varepsilon _ {ijk} a ^ {j} b ^ {k}}$

em que índices repetidos são somados sobre os valores de 1 a 3. Esta representação é outra forma de representação simétrica enviesada do produto vetorial:

${\ displaystyle \ eta ^ {mi} \ varepsilon _ {ijk} a ^ {j} = [\ mathbf {a}] _ {\ times}.}$

Na mecânica clássica : representar o produto vetorial usando o símbolo de Levi-Civita pode fazer com que as simetrias mecânicas sejam óbvias quando os sistemas físicos são isotrópicos . (Um exemplo: considere uma partícula em um potencial da Lei de Hooke em três espaços, livre para oscilar em três dimensões; nenhuma dessas dimensões é "especial" em qualquer sentido, então as simetrias estão no momento angular representado pelo produto cruzado, que são evidenciados pela referida representação Levi-Civita).

Mnemônico

A palavra "xyzzy" pode ser usada para lembrar a definição do produto vetorial.

Se

${\ displaystyle \ mathbf {a} = \ mathbf {b} \ times \ mathbf {c}}$

Onde:

${\ displaystyle \ mathbf {a} = {\ begin {bmatrix} a_ {x} \\ a_ {y} \\ a_ {z} \ end {bmatrix}}, \ \ mathbf {b} = {\ begin {bmatrix } b_ {x} \\ b_ {y} \\ b_ {z} \ end {bmatriz}}, \ \ mathbf {c} = {\ begin {bmatrix} c_ {x} \\ c_ {y} \\ c_ {z} \ end {bmatrix}}}$

então:

${\ displaystyle a_ {x} = b_ {y} c_ {z} -b_ {z} c_ {y}}$

${\ displaystyle a_ {y} = b_ {z} c_ {x} -b_ {x} c_ {z}}$

${\ displaystyle a_ {z} = b_ {x} c_ {y} -b_ {y} c_ {x}.}$

A segunda e a terceira equações podem ser obtidas a partir da primeira simplesmente girando verticalmente os subscritos, x → y → z → x . O problema, claro, é como lembrar a primeira equação, e duas opções estão disponíveis para esse propósito: ou para lembrar as duas diagonais relevantes do esquema de Sarrus (aquelas contendo i ), ou para lembrar a sequência xyzzy.

Como a primeira diagonal no esquema de Sarrus é apenas a diagonal principal da matriz 3 × 3 mencionada acima , as três primeiras letras da palavra xyzzy podem ser facilmente lembradas.

Visualização cruzada

Similarmente ao dispositivo mnemônico acima, uma "cruz" ou X pode ser visualizado entre os dois vetores na equação. Isso pode ser útil para lembrar a fórmula correta do produto vetorial.

Se

${\ displaystyle \ mathbf {a} = \ mathbf {b} \ times \ mathbf {c}}$

então:

${\ displaystyle \ mathbf {a} = {\ begin {bmatrix} b_ {x} \\ b_ {y} \\ b_ {z} \ end {bmatrix}} \ times {\ begin {bmatrix} c_ {x} \ \ c_ {y} \\ c_ {z} \ end {bmatrix}}.}$

Se quisermos obter a fórmula para , simplesmente retiramos o e da fórmula e retiramos os próximos dois componentes: ${\ displaystyle a_ {x}}$${\ displaystyle b_ {x}}$${\ displaystyle c_ {x}}$

${\ displaystyle a_ {x} = {\ begin {bmatrix} b_ {y} \\ b_ {z} \ end {bmatrix}} \ times {\ begin {bmatrix} c_ {y} \\ c_ {z} \ end {bmatrix}}.}$

Ao fazer isso para os próximos dois elementos, deve "envolver" a matriz de forma que após o componente z venha o componente x. Para maior clareza, ao realizar esta operação para , os próximos dois componentes devem ser z e x (nessa ordem). Enquanto para os próximos dois componentes devem ser considerados como x e y. ${\ displaystyle a_ {y}}$${\ displaystyle a_ {y}}$${\ displaystyle a_ {z}}$

${\ displaystyle a_ {y} = {\ begin {bmatrix} b_ {z} \\ b_ {x} \ end {bmatrix}} \ times {\ begin {bmatrix} c_ {z} \\ c_ {x} \ end {bmatriz}}, \ a_ {z} = {\ begin {bmatrix} b_ {x} \\ b_ {y} \ end {bmatrix}} \ times {\ begin {bmatrix} c_ {x} \\ c_ {y } \ end {bmatrix}}}$

Pois então, se visualizarmos o operador de cruz apontando de um elemento da esquerda para um elemento da direita, podemos pegar o primeiro elemento da esquerda e simplesmente multiplicar pelo elemento para o qual a cruz aponta na matriz da direita. Em seguida, subtraímos o próximo elemento à esquerda, multiplicado pelo elemento para o qual a cruz aponta também. Isso resulta em nossa fórmula - ${\ displaystyle a_ {x}}$${\ displaystyle a_ {x}}$

${\ displaystyle a_ {x} = b_ {y} c_ {z} -b_ {z} c_ {y}.}$

Podemos fazer isso da mesma maneira para e para construir suas fórmulas associadas. ${\ displaystyle a_ {y}}$${\ displaystyle a_ {z}}$

Formulários

O produto cruzado tem aplicações em vários contextos. Por exemplo, é usado em geometria computacional, física e engenharia. Segue uma lista não exaustiva de exemplos.

Geometria computacional

O produto vetorial aparece no cálculo da distância de duas linhas de inclinação (linhas que não estão no mesmo plano) uma da outra no espaço tridimensional.

O produto vetorial pode ser usado para calcular a normal para um triângulo ou polígono, uma operação freqüentemente realizada em computação gráfica . Por exemplo, o enrolamento de um polígono (sentido horário ou anti-horário) em torno de um ponto dentro do polígono pode ser calculado triangulando o polígono (como um raio de roda) e somando os ângulos (entre os raios) usando o produto vetorial para manter o controle do sinal de cada ângulo.

Na geometria computacional do plano , o produto vetorial é usado para determinar o sinal do ângulo agudo definido por três pontos e . Corresponde à direção (para cima ou para baixo) do produto vetorial dos dois vetores coplanares definidos pelos dois pares de pontos e . O sinal do ângulo agudo é o sinal da expressão ${\ displaystyle p_ {1} = (x_ {1}, y_ {1}), p_ {2} = (x_ {2}, y_ {2})}$${\ displaystyle p_ {3} = (x_ {3}, y_ {3})}$${\ displaystyle (p_ {1}, p_ {2})}$${\ displaystyle (p_ {1}, p_ {3})}$

${\ displaystyle P = (x_ {2} -x_ {1}) (y_ {3} -y_ {1}) - (y_ {2} -y_ {1}) (x_ {3} -x_ {1}) ,}$

que é o comprimento assinado do produto vetorial dos dois vetores.

No sistema de coordenadas "destro", se o resultado for 0, os pontos são colineares ; se for positivo, os três pontos constituem um ângulo positivo de rotação em torno de a , caso contrário, um ângulo negativo. De outro ponto de vista, o sinal de indica se está à esquerda ou à direita da linha${\ displaystyle p_ {1}}$${\ displaystyle p_ {2}}$${\ displaystyle p_ {3}}$${\ displaystyle P}$${\ displaystyle p_ {3}}$${\ displaystyle p_ {1}, p_ {2}.}$

O produto vetorial é usado no cálculo do volume de um poliedro , como um tetraedro ou paralelepípedo .

Momento angular e torque

O momento angular L de uma partícula sobre uma determinada origem é definido como:

${\ displaystyle \ mathbf {L} = \ mathbf {r} \ times \ mathbf {p},}$

onde r é o vetor de posição da partícula em relação à origem, p é o momento linear da partícula.

Da mesma forma, o momento M de uma força F _B aplicada no ponto B em torno do ponto A é dado como:

${\ displaystyle \ mathbf {M} _ {\ mathrm {A}} = \ mathbf {r} _ {\ mathrm {AB}} \ times \ mathbf {F} _ {\ mathrm {B}} \,}$

Em mecânica, o momento de uma força também é chamado de torque e escrito como${\ displaystyle \ mathbf {\ tau}}$

Como a posição r , o momento linear p e a força F são todos vetores verdadeiros , tanto o momento angular L quanto o momento de uma força M são pseudovetores ou vetores axiais .

Corpo rígido

O produto vetorial freqüentemente aparece na descrição de movimentos rígidos. Dois pontos P e Q em um corpo rígido podem ser relacionados por:

${\ displaystyle \ mathbf {v} _ {P} - \ mathbf {v} _ {Q} = {\ boldsymbol {\ omega}} \ times \ left (\ mathbf {r} _ {P} - \ mathbf {r } _ {Q} \ right) \,}$

onde é a posição do ponto, é sua velocidade e é a velocidade angular do corpo . ${\ displaystyle \ mathbf {r}}$${\ displaystyle \ mathbf {v}}$${\ displaystyle {\ boldsymbol {\ omega}}}$

Visto que posição e velocidade são vetores verdadeiros , a velocidade angular é um pseudovetor ou vetor axial . ${\ displaystyle \ mathbf {r}}$${\ displaystyle \ mathbf {v}}$${\ displaystyle {\ boldsymbol {\ omega}}}$

Força Lorentz

O produto vetorial é usado para descrever a força de Lorentz experimentada por uma carga elétrica em movimento q _e :

${\ displaystyle \ mathbf {F} = q_ {e} \ left (\ mathbf {E} + \ mathbf {v} \ times \ mathbf {B} \ right)}$

Como a velocidade v , a força F e o campo elétrico E são todos vetores verdadeiros , o campo magnético B é um pseudovetor .

De outros

No cálculo vetorial , o produto vetorial é usado para definir a fórmula para o operador vetorial curl .

O truque de reescrever um produto vetorial em termos de multiplicação de matriz aparece frequentemente na geometria epipolar e de múltiplas visualizações, em particular ao derivar restrições correspondentes.

Como um produto externo

O produto vetorial pode ser definido em termos do produto externo. Pode ser generalizado para um produto externo em outras três dimensões. Esta visualização permite uma interpretação geométrica natural do produto vetorial. Na álgebra exterior, o produto exterior de dois vetores é um bivetor. Um bivetor é um elemento plano orientado, da mesma forma que um vetor é um elemento de linha orientado. Dados dois vectores de um e b , pode-se ver o bivector um ∧ b como o paralelogramo orientado gerado por um e b . O produto vetorial é então obtido tomando a estrela de Hodge do bivetor a ∧ b , mapeando 2 vetores em vetores:

${\ displaystyle a \ times b = \ star (a \ wedge b) \,}$

Isso pode ser considerado como o elemento multidimensional orientado "perpendicular" ao bivetor. Apenas em três dimensões o resultado é um elemento unidimensional orientado - um vetor - enquanto, por exemplo, em quatro dimensões o Hodge dual de um bivetor é bidimensional - um bivetor. Assim, apenas em três dimensões pode um produto cruzado vetor de um e b ser definida como o vector de dupla para o bivector um ∧ b : é perpendicular ao bivector, com orientação dependente de destreza manual do sistema de coordenadas, e tem a mesma magnitude relativa ao vetor normal unitário como a ∧ b tem em relação ao bivetor unitário; precisamente as propriedades descritas acima.

Handedness

Consistência

Quando as leis da física são escritas como equações, é possível fazer uma escolha arbitrária do sistema de coordenadas, incluindo a destreza. Deve-se ter cuidado para nunca escrever uma equação em que os dois lados não se comportem igualmente em todas as transformações que precisam ser consideradas. Por exemplo, se um lado da equação é um produto vetorial de dois vetores polares, deve-se levar em consideração que o resultado é um vetor axial . Portanto, para consistência, o outro lado também deve ser um vetor axial. Mais geralmente, o resultado de um produto vetorial pode ser um vetor polar ou um vetor axial, dependendo do tipo de seus operandos (vetores polares ou vetores axiais). Nomeadamente, os vetores polares e os vetores axiais estão inter-relacionados das seguintes maneiras sob a aplicação do produto vetorial:

• vetor polar × vetor polar = vetor axial
• vetor axial × vetor axial = vetor axial
• vetor polar × vetor axial = vetor polar
• vetor axial × vetor polar = vetor polar

ou simbolicamente

• polar × polar = axial
• axial × axial = axial
• polar × axial = polar
• axial × polar = polar

Como o produto vetorial também pode ser um vetor polar, ele pode não mudar de direção com uma transformação de imagem espelhada. Isso acontece, de acordo com as relações acima, se um dos operandos for um vetor polar e o outro for um vetor axial (por exemplo, o produto vetorial de dois vetores polares). Por exemplo, um produto triplo vetorial envolvendo três vetores polares é um vetor polar.

Uma abordagem livre de lateralidade é possível usando álgebra exterior.

O paradoxo da base ortonormal

Seja ( i , j , k ) uma base ortonormal. Os vetores i , j e k não dependem da orientação do espaço. Eles podem até ser definidos na ausência de qualquer orientação. Portanto, eles não podem ser vetores axiais. Mas se i e j são vetores polares, então k é um vetor axial para i × j = k ou j × i = k . Este é um paradoxo.

"Axial" e "polar" são físicas qualificadores para físicos vectores; ou seja, vetores que representam quantidades físicas , como a velocidade ou o campo magnético. Os vetores i , j e k são vetores matemáticos, nem axiais nem polares. Em matemática, o produto cruzado de dois vetores é um vetor. Não há contradição.

Generalizações

Existem várias maneiras de generalizar o produto vetorial para dimensões superiores.

Álgebra de mentira

O produto vetorial pode ser visto como um dos produtos de Lie mais simples e, portanto, é generalizado pelas álgebras de Lie , que são axiomatizadas como produtos binários que satisfazem os axiomas de multilinearidade, simetria de inclinação e a identidade de Jacobi. Existem muitas álgebras de Lie e seu estudo é um campo importante da matemática, chamado teoria de Lie .

Por exemplo, a álgebra de Heisenberg fornece outra estrutura de álgebra de Lie com base no produto é${\ displaystyle \ mathbf {R} ^ {3}.}$${\ displaystyle \ {x, y, z \},}$${\ displaystyle [x, y] = z, [x, z] = [y, z] = 0.}$

Quatérnions

O produto vetorial também pode ser descrito em termos de quatérnios . Em geral, se um vetor [ a ₁ , a ₂ , a ₃ ] é representado como o quatérnion a ₁ i + a ₂ j + a ₃ k , o produto vetorial de dois vetores pode ser obtido tomando seu produto como quatérnions e deletando a parte real do resultado. A parte real será o negativo do produto escalar dos dois vetores.

Octonions

Um produto vetorial para vetores de 7 dimensões pode ser obtido da mesma forma, usando as octonions em vez dos quaternions. A inexistência de produtos cruzados não triviais com valor vetorial de dois vetores em outras dimensões está relacionada ao resultado do teorema de Hurwitz de que as únicas álgebras de divisão normada são aquelas com dimensão 1, 2, 4 e 8.

Produto exterior

Na dimensão geral, não há um análogo direto do produto vetorial binário que produz especificamente um vetor. No entanto, existe o produto exterior, que tem propriedades semelhantes, exceto que o produto exterior de dois vetores é agora um vetor 2 em vez de um vetor comum. Como mencionado acima, o produto vetorial pode ser interpretado como o produto externo em três dimensões usando o operador estrela de Hodge para mapear 2 vetores em vetores. O dual de Hodge do produto externo produz um ( n - 2) -vetor, que é uma generalização natural do produto vetorial em qualquer número de dimensões.

O produto externo e o produto escalar podem ser combinados (por meio de soma) para formar o produto geométrico em álgebra geométrica.

Produto externo

Conforme mencionado acima, o produto vetorial pode ser interpretado em três dimensões como o Hodge dual do produto externo. Em quaisquer n dimensões finitas , o dual de Hodge do produto exterior de n - 1 vetores é um vetor. Assim, em vez de uma operação binária, em dimensões finitas arbitrárias, o produto vetorial é generalizado como o dual de Hodge do produto exterior de alguns n - 1 vetores dados. Essa generalização é chamada de produto externo .

Produto comutador

Interpretação do tridimensional de espaço vectorial da álgebra como o 2-vector (não o 1-vector) subálgebra da álgebra geométrica tridimensional, onde , , e , os corresponde produto cruzado exactamente ao produto comutador em álgebra geométrica e tanto use o mesmo símbolo . O produto do comutador é definido para 2 vetores e em álgebra geométrica como: ${\ displaystyle \ mathbf {i} = \ mathbf {e_ {2}} \ mathbf {e_ {3}}}$${\ displaystyle \ mathbf {j} = \ mathbf {e_ {1}} \ mathbf {e_ {3}}}$${\ displaystyle \ mathbf {k} = \ mathbf {e_ {1}} \ mathbf {e_ {2}}}$${\ displaystyle \ times}$${\ displaystyle A}$${\ displaystyle B}$

${\ displaystyle A \ times B = {\ tfrac {1} {2}} (AB-BA)}$

onde está o produto geométrico. ${\ displaystyle AB}$

O produto do comutador poderia ser generalizado para multivetores arbitrários em três dimensões, o que resulta em um multivetor consistindo apenas de elementos de graus 1 (1-vetor / vetores verdadeiros ) e 2 (2-vetores / pseudovetores). Enquanto o produto do comutador de dois vetores 1 é de fato o mesmo que o produto externo e produz um vetor 2, o comutador de um vetor 1 e um vetor 2 produz um vetor verdadeiro, correspondendo em vez das contrações esquerda e direita em álgebra geométrica. O produto do comutador de dois 2 vetores não tem produto equivalente correspondente, razão pela qual o produto do comutador é definido em primeiro lugar para 2 vetores. Além disso, o produto triplo do comutador de três 2 vetores é o mesmo que o produto triplo do vetor dos mesmos três pseudovetores na álgebra vetorial. No entanto, o produto triplo do comutador de três vetores 1 na álgebra geométrica é, em vez disso, o negativo do produto triplo do vetor dos mesmos três vetores verdadeiros na álgebra vetorial.

Generalizações para dimensões superiores são fornecidas pelo mesmo produto comutador de 2 vetores em álgebras geométricas de dimensões superiores, mas os 2 vetores não são mais pseudovetores. Assim como o produto / produto vetorial do comutador de 2 vetores em três dimensões corresponde à álgebra de Lie mais simples , as subálgebras de 2 vetores da álgebra geométrica de dimensão superior equipadas com o produto do comutador também correspondem às álgebras de Lie. Também como em três dimensões, o produto do comutador poderia ser generalizado para multivetores arbitrários.

Álgebra multilinear

No contexto da álgebra multilinear , o produto vetorial pode ser visto como o (1,2) -tensor (um tensor misto , especificamente um mapa bilinear ) obtido a partir da forma de volume tridimensional , um (0,3) -tensor, por levantar um índice .

Em detalhes, a forma de volume tridimensional define um produto tomando o determinante da matriz dado por esses 3 vetores. Por dualidade , isso é equivalente a uma função (fixar quaisquer duas entradas dá uma função avaliando na terceira entrada) e na presença de um produto interno (como o produto escalar; mais geralmente, uma forma bilinear não degenerada), temos um isomorfismo e, portanto, isso produz um mapa que é o produto vetorial: um (0,3) -tensor (3 entradas de vetor, saída escalar) foi transformado em um (1,2) -tensor (2 entradas de vetor, 1 saída do vetor) "aumentando um índice". ${\ displaystyle V \ times V \ times V \ to \ mathbf {R},}$${\ displaystyle V \ times V \ a V ^ {*},}$${\ displaystyle V \ to \ mathbf {R}}$${\ displaystyle V \ a V ^ {*},}$${\ displaystyle V \ times V \ a V,}$

Traduzindo a álgebra acima em geometria, a função "volume do paralelepípedo definido por " (em que os dois primeiros vetores são fixos e o último é uma entrada), que define uma função , pode ser representada exclusivamente como o produto escalar com um vetor: este vetor é o produto vetorial Nesta perspectiva, o produto vetorial é definido pelo produto escalar triplo ,${\ displaystyle (a, b, -)}$${\ displaystyle V \ to \ mathbf {R}}$${\ displaystyle a \ times b.}$${\ displaystyle \ mathrm {Vol} (a, b, c) = (a \ vezes b) \ cdot c.}$

Da mesma forma, em dimensões superiores, pode-se definir produtos cruzados generalizados elevando os índices da forma de volume n- dimensional, que é um -tensor. As generalizações mais diretas do produto vetorial são para definir: ${\ displaystyle (0, n)}$

• um -tensor, que toma como vetores de entrada , e dá como saída 1 vetor - um produto com valor de vetor -ary, ou${\ displaystyle (1, n-1)}$${\ displaystyle n-1}$${\ displaystyle (n-1)}$
• um -tensor, que toma como entrada 2 vetores e dá como saída tensor simétrico com inclinação de classificação n - 2 - um produto binário com classificação n - 2 valores de tensor. Também se pode definir -tensores para outros k .${\ displaystyle (n-2,2)}$${\ displaystyle (k, nk)}$

Esses produtos são todos multilineares e simétricos com inclinação e podem ser definidos em termos de determinante e paridade .

O produto -ary pode ser descrito como se segue: dadas vectores em definir o seu produto cruzado generalizada como: ${\ displaystyle (n-1)}$${\ displaystyle n-1}$${\ displaystyle v_ {1}, \ dots, v_ {n-1}}$${\ displaystyle \ mathbf {R} ^ {n},}$${\ displaystyle v_ {n} = v_ {1} \ times \ cdots \ times v_ {n-1}}$

• perpendicular ao hiperplano definido pelo ${\ displaystyle v_ {i},}$
• magnitude é o volume do paralelotopo definido pelo que pode ser calculado como o determinante de Gram do${\ displaystyle v_ {i},}$${\ displaystyle v_ {i},}$
• orientado para que seja orientado positivamente.${\ displaystyle v_ {1}, \ dots, v_ {n}}$

Este é o produto multilinear alternado único que avalia , e assim por diante, para permutações cíclicas de índices. ${\ displaystyle e_ {1} \ times \ cdots \ times e_ {n-1} = e_ {n}}$${\ displaystyle e_ {2} \ times \ cdots \ times e_ {n} = e_ {1},}$

Em coordenadas, pode-se dar uma fórmula para este análogo -ary do produto vetorial em R ⁿ por: ${\ displaystyle (n-1)}$

${\ displaystyle \ bigwedge _ {i = 0} ^ {n-1} \ mathbf {v} _ {i} = {\ begin {vmatrix} v_ {1} {} ^ {1} & \ cdots & v_ {1} {} ^ {n} \\\ vdots & \ ddots & \ vdots \\ v_ {n-1} {} ^ {1} & \ cdots & v_ {n-1} {} ^ {n} \\\ mathbf { e} _ {1} & \ cdots & \ mathbf {e} _ {n} \ end {vmatrix}}.}$

Esta fórmula é idêntica em estrutura à fórmula do determinante para o produto vetorial normal em R ^3, exceto que a linha de vetores de base é a última linha no determinante, e não a primeira. A razão para isso é garantir que os vetores ordenados ( v ₁ , ..., v _{n −1} , Λ^{n –1}
_{i = 0}v _i ) ter uma orientação positiva em relação a ( e ₁ , ..., e _n ). Se n for ímpar, essa modificação deixa o valor inalterado, portanto, essa convenção está de acordo com a definição normal do produto binário. No caso de n ser par, entretanto, a distinção deve ser mantida. Esta forma -ary possui muitas das mesmas propriedades que o produto vetorial vetorial: é alternada e linear em seus argumentos, é perpendicular a cada argumento e sua magnitude fornece o hipervolume da região delimitada pelos argumentos. E, assim como o produto vetorial vetorial, ele pode ser definido de uma maneira independente de coordenadas como o dual de Hodge do produto em cunha dos argumentos. ${\ displaystyle (n-1)}$

História

Em 1773, Joseph-Louis Lagrange introduziu a forma do componente tanto do ponto quanto do produto cruzado para estudar o tetraedro em três dimensões. Em 1843, William Rowan Hamilton introduziu o produto quaternion e com ele os termos "vetor" e "escalar". Dado dois quatérnions [0, L ] e [0, v ] , onde u e v são vectores em R ³ , o seu produto Quatérnion pode ser resumido como [- u ⋅ v , u × v ] . James Clerk Maxwell usou as ferramentas de quatérnio de Hamilton para desenvolver suas famosas equações de eletromagnetismo e, por esta e outras razões, os quatérnios por um tempo foram uma parte essencial da educação física.

Em 1878, William Kingdon Clifford publicou seu Elements of Dynamic, um texto avançado para a época. Ele definiu o produto de dois vetores como tendo magnitude igual à área do paralelogramo do qual eles são dois lados, e direção perpendicular ao seu plano.

Oliver Heaviside e Josiah Willard Gibbs também sentiram que os métodos do quaternion eram muito complicados, muitas vezes exigindo que a parte escalar ou vetorial de um resultado fosse extraída. Assim, cerca de quarenta anos após o produto do quatérnio, o produto escalar e o produto vetorial foram introduzidos - sob forte oposição. Fundamental para a (eventual) aceitação foi a eficiência da nova abordagem, permitindo a Heaviside reduzir as equações do eletromagnetismo das 20 originais de Maxwell às quatro comumente vistas hoje.

Em grande parte independente desse desenvolvimento e pouco apreciado na época, Hermann Grassmann criou uma álgebra geométrica não ligada à dimensão dois ou três, com o produto externo desempenhando um papel central. Em 1853, Augustin-Louis Cauchy , contemporâneo de Grassmann, publicou um artigo sobre chaves algébricas que eram usadas para resolver equações e tinham as mesmas propriedades de multiplicação do produto vetorial. Clifford combinou as álgebras de Hamilton e Grassmann para produzir a álgebra de Clifford , onde, no caso de vetores tridimensionais, o bivetor produzido a partir de dois vetores dualiza em um vetor, reproduzindo assim o produto vetorial.

A notação cruzada e o nome "produto cruzado" começaram com Gibbs. Originalmente, eles apareceram em notas publicadas privadamente para seus alunos em 1881 como Elementos de análise vetorial . A utilidade para a mecânica foi observada por Aleksandr Kotelnikov . A notação de Gibbs e o nome "produto cruzado" mais tarde alcançaram um amplo público por meio de Vector Analysis , um livro de Edwin Bidwell Wilson , um ex-aluno. Wilson reorganizou o material das palestras de Gibbs, junto com o material das publicações de Heaviside, Föpps e Hamilton. Ele dividiu a análise vetorial em três partes:

Primeiro, o que diz respeito à adição e aos produtos escalares e vetoriais dos vetores. Em segundo lugar, o que diz respeito ao cálculo diferencial e integral em suas relações com funções escalares e vetoriais. Terceiro, aquele que contém a teoria da função vetorial linear.

Dois tipos principais de multiplicações de vetores foram definidos e chamados da seguinte forma:

• O directo , escalar , ou dot produto de dois vetores
• A inclinação , vetor ou produto cruzado de dois vetores

Vários tipos de produtos triplos e produtos de mais de três vetores também foram examinados. A expansão tripla de produto acima mencionada também foi incluída.

Veja também

• Produto cartesiano - Um produto de dois conjuntos
• Álgebra geométrica: sistemas rotativos
• Vários produtos cruzados - produtos envolvendo mais de três vetores
• Multiplicação de vetores
• Produto quádruplo
• × (o símbolo)

Notas

Referências

Bibliografia

• Cajori, Florian (1929). A History Of Mathematical Notations Volume II . Publicação em tribunal aberto . p. 134. ISBN 978-0-486-67766-8.
• EA Milne (1948) Vectorial Mechanics , Capítulo 2: Vector Product, pp 11–31, London: Methuen Publishing .
• Wilson, Edwin Bidwell (1901). Análise de vetores: um livro-texto para uso de estudantes de matemática e física, baseado nas palestras de J. Willard Gibbs . Yale University Press .
• T. Levi-Civita; U. Amaldi (1949). Lezioni di meccanica razionale (em italiano). Bolonha: Zanichelli editore.

links externos

• "Produto cruzado" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Uma rápida derivação geométrica e interpretação de produtos cruzados
• Um tutorial interativo criado na Syracuse University - (requer java )
• W. Kahan (2007). Produtos cruzados e rotações no espaço euclidiano 2 e 3. Universidade da Califórnia, Berkeley (PDF).
• O produto vetorial , Mathcentre (Reino Unido), 2009