Treliça Bravais - Bravais lattice

Em geometria e cristalografia , uma rede de Bravais , em homenagem a Auguste Bravais ( 1850 ), é uma matriz infinita de pontos discretos gerados por um conjunto de operações de translação discretas descritas no espaço tridimensional por:

{\ displaystyle \ mathbf {R} = n_ {1} \ mathbf {a} _ {1} + n_ {2} \ mathbf {a} _ {2} + n_ {3} \ mathbf {a} _ {3} }

onde os n _i são quaisquer inteiros e a _i são vetores de tradução primitivos ou vetores primitivos que se encontram em direções diferentes (não necessariamente perpendiculares entre si) e abrangem a rede. A escolha de vetores primitivos para uma dada rede de Bravais não é única. Um aspecto fundamental de qualquer rede Bravais é que, para qualquer escolha de direção, a rede aparecerá exatamente a mesma de cada um dos pontos discretos da rede ao olhar para aquela direção escolhida.

O conceito de rede de Bravais é usado para definir formalmente um arranjo cristalino e suas fronteiras (finitas). Um cristal é feito de um ou mais átomos, chamados de base ou motivo , em cada ponto da rede. A base pode consistir em átomos , moléculas ou cadeias de polímeros de matéria sólida , e a rede fornece as localizações da base.

Duas redes Bravais são freqüentemente consideradas equivalentes se tiverem grupos de simetria isomórfica. Nesse sentido, existem 5 redes Bravais possíveis no espaço bidimensional e 14 redes Bravais possíveis no espaço tridimensional. Os 14 grupos de simetria possíveis das redes Bravais são 14 dos 230 grupos espaciais . No contexto da classificação do grupo espacial, as redes Bravais são também chamadas de classes Bravais, classes aritméticas Bravais ou rebanhos Bravais.

Célula unitária

Na cristalografia, existe o conceito de uma célula unitária que compreende o espaço entre os pontos adjacentes da rede, bem como quaisquer átomos nesse espaço. Uma célula unitária é definida como um espaço que, quando traduzido através de um subconjunto de todos os vetores descritos por , preenche o espaço da rede sem sobreposição ou vazios. (Ou seja, um espaço de rede é um múltiplo de uma célula unitária.) Existem basicamente dois tipos de células unitárias: células unitárias primitivas e células unitárias convencionais. Uma célula primitiva é o menor componente de uma rede (ou cristal) que, quando empilhada com as operações de tradução da rede, reproduz toda a rede (ou cristal). Observe que as traduções devem ser operações de tradução de rede que fazem com que a rede apareça inalterada após a tradução. Se traduções arbitrárias fossem permitidas, poderia-se fazer uma célula primitiva com a metade do tamanho da verdadeira e traduzir duas vezes mais, por exemplo. Outra forma de definir o tamanho de uma célula primitiva que evita invocar operações de tradução de rede é dizer que a célula primitiva é o menor componente possível de uma rede (ou cristal) que pode ser repetido para reproduzir toda a rede (ou cristal), e que contém exatamente um ponto de rede. Em qualquer definição, a célula primitiva é caracterizada por seu pequeno tamanho. Existem claramente muitas opções de células que podem reproduzir toda a rede quando empilhadas (duas metades da rede, por exemplo), e o requisito de tamanho mínimo distingue a célula primitiva de todas essas outras unidades repetitivas válidas. Se a rede ou cristal é bidimensional, a célula primitiva tem uma área mínima; da mesma forma, em 3 dimensões, a célula primitiva tem um volume mínimo. Apesar desse rígido requisito de tamanho mínimo, não há uma escolha única de célula unitária primitiva. Na verdade, todas as células cujas bordas são vetores de tradução primitivos serão células unitárias primitivas. O fato de não haver uma escolha única de vetores de tradução primitivos para uma determinada rede leva à multiplicidade de células unitárias primitivas possíveis. As células unitárias convencionais, por outro lado, não são necessariamente células de tamanho mínimo. Eles são escolhidos puramente por conveniência e costumam ser usados para fins ilustrativos. Eles são definidos vagamente. ${\ displaystyle \ mathbf {R} = n_ {1} \ mathbf {a} _ {1} + n_ {2} \ mathbf {a} _ {2} + n_ {3} \ mathbf {a} _ {3} }$

As células unitárias primitivas são definidas como células unitárias com o menor volume para um determinado cristal. (Um cristal é uma rede e uma base em cada ponto da rede.) Para ter o menor volume de célula, uma célula unitária primitiva deve conter (1) apenas um ponto da rede e (2) a quantidade mínima de constituintes básicos (por exemplo, o mínimo número de átomos em uma base). Para o primeiro requisito, contar o número de pontos de rede em uma célula unitária é tal que, se um ponto de rede é compartilhado por m células unitárias adjacentes em torno desse ponto de rede, então o ponto é contado como 1 / m . O último requisito é necessário, uma vez que existem cristais que podem ser descritos por mais de uma combinação de uma rede e uma base. Por exemplo, um cristal, visto por uma rede com átomos de tipo único localizados em cada ponto da rede (a forma de base mais simples), também pode ser visto por outra rede com uma base de dois átomos. Neste caso, uma célula unitária primitiva é uma célula unitária tendo apenas um ponto de rede na primeira forma de descrever o cristal, a fim de garantir o menor volume de célula unitária.

Pode haver mais de uma maneira de escolher uma célula primitiva para um determinado cristal e cada escolha terá uma forma de célula primitiva diferente, mas o volume da célula primitiva é o mesmo para todas as opções e cada escolha terá a propriedade de um para - uma correspondência pode ser estabelecida entre células unitárias primitivas e pontos de rede discretos sobre a rede associada. Todas as células unitárias primitivas com formas diferentes para um dado cristal têm o mesmo volume por definição; Para um dado cristal, se n é a densidade dos pontos da rede em uma rede garantindo a quantidade mínima de constituintes básicos ev é o volume de uma célula primitiva escolhida, então nv = 1 resultando em v = 1 / n , então cada célula primitiva tem o mesmo volume de 1 / n .

Entre todas as células primitivas possíveis para um determinado cristal, uma célula primitiva óbvia pode ser o paralelepípedo formado por um conjunto escolhido de vetores de tradução primitivos. (Novamente, esses vetores devem formar uma rede com a quantidade mínima de constituintes básicos.) Ou seja, o conjunto de todos os pontos onde e é o vetor primitivo escolhido. Esta célula primitiva nem sempre mostra a simetria nítida de um determinado cristal. Neste caso, uma célula unitária convencional exibindo facilmente a simetria do cristal é freqüentemente usada. O volume da célula unitária convencional será um número inteiro múltiplo do volume da célula unitária primitiva. ${\ displaystyle \ mathbf {r} = x_ {1} \ mathbf {a} _ {1} + x_ {2} \ mathbf {a} _ {2} + x_ {3} \ mathbf {a} _ {3} }$ ${\ displaystyle 0 \ leq x_ {i} <1}$ ${\ displaystyle \ mathbf {a} _ {i}}$

Origem do conceito

Em duas dimensões, qualquer rede pode ser especificada pelo comprimento de seus dois vetores de translação primitivos e o ângulo entre eles. Há um número infinito de redes possíveis que podem ser descritas dessa maneira. Alguma maneira de categorizar diferentes tipos de reticulados é desejada. Uma maneira de fazer isso é reconhecer que algumas redes têm simetria inerente. Pode-se impor condições no comprimento dos vetores de translação primitivos e no ângulo entre eles para produzir várias redes simétricas. Essas simetrias são categorizadas em diferentes tipos, como simetrias de espelho, simetrias de inversão, simetrias de rotação e simetrias de translação. Uma combinação particular dessas simetrias (por exemplo, simetria de rotação dupla e simetria de espelho) é chamada de grupo de pontos . Assim, os reticulados podem ser categorizados com base no grupo de pontos que se aplica a eles. O grupo de pontos mais básico corresponde à invariância rotacional sob 2π e π, ou simetria rotacional de 1 e 2 vezes. Na verdade, isso se aplica automaticamente a todas as redes bidimensionais e é o grupo de pontos mais geral. Os reticulados contidos neste grupo (tecnicamente todos os reticulados, mas convencionalmente todos os reticulados que não se enquadram em nenhum dos outros grupos de pontos) são chamados de reticulados oblíquos . A partir daí, em duas dimensões, existem 4 grupos de pontos adicionais (ou equivalentemente, 4 tipos de restrição nos comprimentos / ângulos dos vetores de translação primitivos) que correspondem às 4 categorias de rede restantes: quadrada, hexagonal, retangular e retangular centrada . Assim, ao todo, existem 5 redes Bravais em 2 dimensões. Da mesma forma, em 3 dimensões, existem 14 treliças Bravais: 1 categoria geral "cesto de lixo" ( triclínico ) e mais 13 categorias. Esses 14 tipos de rede são agrupados por conveniência em 7 sistemas de rede (triclínico, monoclínico, ortorrômbico, tetragonal, cúbico, trigonal e hexagonal).

Em 2 dimensões

No espaço bidimensional, existem 5 redes Bravais, agrupadas em quatro famílias de cristais .

Nota: Nos diagramas de células unitárias da tabela a seguir, os pontos da rede são representados com círculos pretos e as células unitárias são representadas com paralelogramos (que podem ser quadrados ou retângulos) delineados em preto. Embora cada um dos quatro cantos de cada paralelogramo se conecte a um ponto da rede, apenas um dos quatro pontos da rede pertence tecnicamente a uma determinada célula unitária e cada um dos outros três pontos da rede pertence a uma das células unitárias adjacentes. Isso pode ser visto imaginando mover o paralelogramo da célula unitária ligeiramente para a esquerda e ligeiramente para baixo, enquanto deixa todos os círculos pretos dos pontos da rede fixos.

Família cristal	Grupo de pontos ( notação Schönflies )	5 treliças Bravais
Família cristal	Grupo de pontos ( notação Schönflies )	Primitivo (p)	Centrado (c)
Monoclínico (m)	C ₂	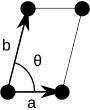Oblíquo (mp)
Ortorrômbico (o)	D ₂	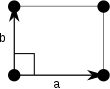Retangular (op)	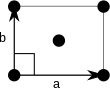Retangular centrado (oc)
Tetragonal (t)	D ₄	Quadrado (tp)
Hexagonal (h)	D ₆	Hexagonal (hp)

As células unitárias são especificadas de acordo com os comprimentos relativos das bordas de células ( um e b ) e o ângulo entre eles ( θ ). A área da célula unitária pode ser calculada avaliando a norma || a × b || , onde a e b são os vetores da rede. As propriedades das famílias de cristal são fornecidas abaixo:

Família cristal	Área	Distâncias axiais (comprimentos de borda)	Ângulo axial
Monoclínico	${\ displaystyle ab \, \ sin \ theta}$	a ≠ b	θ ≠ 90 °
Ortorrômbico	${\ displaystyle ab}$	a ≠ b	θ = 90 °
Tetragonal	${\ displaystyle a ^ {2}}$	a = b	θ = 90 °
Hexagonal	${\ displaystyle {\ frac {\ sqrt {3}} {2}} \, a ^ {2}}$	a = b	θ = 120 °

Em 3 dimensões

2 × 2 × 2 células unitárias de uma rede cúbica de diamante

No espaço tridimensional, existem 14 redes Bravais. Estes são obtidos combinando um dos sete sistemas de rede com um dos tipos de centralização. Os tipos de centralização identificam as localizações dos pontos de rede na célula unitária da seguinte forma:

Primitivo (P): pontos de rede apenas nos cantos das células (às vezes chamados de simples)
Centrado na base (A, B ou C): pontos de rede nos cantos da célula com um ponto adicional no centro de cada face de um par de faces paralelas da célula (às vezes chamado de centralizado na extremidade)
Centrado no corpo (I): pontos de rede nos cantos da célula, com um ponto adicional no centro da célula
Centrado na face (F): pontos de rede nos cantos da célula, com um ponto adicional no centro de cada uma das faces da célula

Nem todas as combinações de sistemas de rede e tipos de centralização são necessárias para descrever todas as redes possíveis, pois pode ser mostrado que vários deles são de fato equivalentes uns aos outros. Por exemplo, a rede monoclínica I pode ser descrita por uma rede monoclínica C por diferentes escolhas de eixos de cristal. Da mesma forma, todas as redes centradas em A ou B podem ser descritas por uma centralização em C ou em P. Isso reduz o número de combinações para 14 redes Bravais convencionais, mostrado na tabela abaixo. Abaixo de cada diagrama está o símbolo de Pearson para essa rede Bravais.

Nota: Nos diagramas de células unitárias na tabela a seguir, todos os pontos de rede no limite da célula (cantos e faces) são mostrados; entretanto, nem todos esses pontos da rede pertencem tecnicamente à célula unitária dada. Isso pode ser visto imaginando mover a célula unitária ligeiramente na direção negativa de cada eixo, enquanto mantém os pontos da rede fixos. Grosso modo, isso pode ser pensado como mover a célula unitária ligeiramente para a esquerda, ligeiramente para baixo e ligeiramente para fora da tela. Isso mostra que apenas um dos oito pontos da rede de canto (especificamente o frontal, esquerdo e inferior) pertence à célula unitária dada (os outros sete pontos da rede pertencem a células unitárias adjacentes). Além disso, apenas um dos dois pontos de rede mostrados na face superior e inferior da coluna Centrada na base pertence à célula unitária dada. Finalmente, apenas três dos seis pontos da rede nas faces da coluna centrada na face pertencem à célula unitária dada.

Família cristal	Sistema de treliça	Grupo de pontos ( notação Schönflies )	14 treliças Bravais
Família cristal	Sistema de treliça	Grupo de pontos ( notação Schönflies )	Primitivo (P)	Centrado na base (S)	Centrado no corpo (I)	Centrado no rosto (F)
Triclínico (a)		C _i	aP
Monoclínico (m)		C _2h	mP	em
Ortorrômbico (o)		D _2h	oP	oS	oI	do
Tetragonal (t)		D _4h	tP		tI
Hexagonal (h)	Romboédrico	D _3d	hR
Hexagonal (h)	Hexagonal	D _6h	hP
Cúbico (c)		O _h	cP		cI	cF

As células unitárias são especificadas de acordo com seis parâmetros de rede que são os comprimentos relativos das bordas das células ( a , b , c ) e os ângulos entre elas ( α , β , γ ). O volume da célula unitária pode ser calculado avaliando o produto triplo a · ( b × c ) , onde a , b e c são os vetores da rede. As propriedades dos sistemas de rede são dadas abaixo:

Família cristal	Sistema de treliça	Volume	Distâncias axiais (comprimentos de borda)	Ângulos axiais	Exemplos correspondentes
Triclínico		${\ displaystyle abc {\ sqrt {1- \ cos ^ {2} \ alpha - \ cos ^ {2} \ beta - \ cos ^ {2} \ gamma +2 \ cos \ alpha \ cos \ beta \ cos \ gamma }}}$	(Todos os casos restantes)		K ₂ Cr ₂ O ₇ , CuSO ₄ · 5H ₂ O , H ₃ BO ₃
Monoclínico		${\ displaystyle abc \, \ sin \ beta}$	a ≠ c	α = γ = 90 °, β ≠ 90 °	Enxofre monoclínico , Na ₂ SO ₄ · 10H ₂ O , PbCrO ₃
Ortorrômbico		${\ displaystyle abc}$	a ≠ b ≠ c	α = β = γ = 90 °	Enxofre rômbico , KNO ₃ , BaSO ₄
Tetragonal		${\ displaystyle a ^ {2} c}$	a = b ≠ c	α = β = γ = 90 °	Estanho branco , SnO ₂ , TiO ₂ , CaSO ₄
Hexagonal	Romboédrico	${\ displaystyle a ^ {3} {\ sqrt {1-3 \ cos ^ {2} \ alpha +2 \ cos ^ {3} \ alpha}}}$	a = b = c	α = β = γ ≠ 90 °	Calcita (CaCO ₃ ), cinábrio (HgS)
Hexagonal	Hexagonal	${\ displaystyle {\ frac {\ sqrt {3}} {2}} \, a ^ {2} c}$	a = b	α = β = 90 °, γ = 120 °	Grafite , ZnO , CdS
Cúbico		${\ displaystyle a ^ {3}}$	a = b = c	α = β = γ = 90 °	NaCl , mistura de zinco , cobre metálico , KCl , diamante , prata

Em 4 dimensões

Em quatro dimensões, existem 64 treliças Bravais. Destes, 23 são primitivos e 41 são centralizados. Dez redes Bravais dividem-se em pares enantiomórficos .

Veja também

Referências

Leitura adicional

Bravais, A. (1850). "Mémoire sur les systèmes formés par les points distribués régulièrement sur un plan ou dans l'espace" [Memória sobre os sistemas formados por pontos regularmente distribuídos em um plano ou no espaço]. J. École Polytech . 19 : 1–128. (Inglês: Memoir 1, Crystallographic Society of America, 1949.)
Hahn, Theo, ed. (2002). Tabelas Internacionais de Cristalografia, Volume A: Simetria de Grupo Espacial . Tabelas Internacionais de Cristalografia. A (5ª ed.). Berlim, Nova York: Springer-Verlag . doi : 10.1107 / 97809553602060000100 . ISBN 978-0-7923-6590-7.

links externos

Catálogo de Lattices (por Nebe e Sloane)
Smith, Walter Fox (2002). "A Canção dos Lattices de Bravais" .

Languages

In other projects