Wavelet Daubechies - Daubechies wavelet
As wavelets Daubechies , baseadas no trabalho de Ingrid Daubechies , são uma família de wavelets ortogonais que definem uma transformada wavelet discreta e caracterizada por um número máximo de momentos de desaparecimento para algum suporte dado . Com cada tipo de wavelet desta classe, existe uma função de escala (chamada wavelet pai ) que gera uma análise de multiresolução ortogonal .
Propriedades
Em geral, as wavelets Daubechies são escolhidos para ter o maior número Um de desaparecer momentos, (isso não implica a melhor suavidade) para determinada largura de apoio (número de coeficientes) 2 A . Existem dois esquemas de nomenclatura em uso, D N usando o comprimento ou número de toques e db A referindo-se ao número de momentos de fuga. Portanto, D4 e db2 são a mesma transformação wavelet.
Dentre as 2 A −1 possíveis soluções das equações algébricas para as condições de momento e ortogonalidade, é escolhida aquela cujo filtro de escala tem fase extrema. A transformada wavelet também é fácil de colocar em prática usando a transformada wavelet rápida . As wavelets Daubechies são amplamente utilizadas na solução de uma ampla gama de problemas, por exemplo, propriedades de auto-similaridade de um sinal ou problemas fractais , descontinuidades de sinal, etc.
As wavelets Daubechies não são definidas em termos das funções de escala e wavelet resultantes; na verdade, não é possível escrevê- los de forma fechada . Os gráficos abaixo são gerados usando o algoritmo em cascata , uma técnica numérica que consiste na transformação inversa [1 0 0 0 0 ...] um número apropriado de vezes.
| Funções de escala e wavelet |

|

|

|
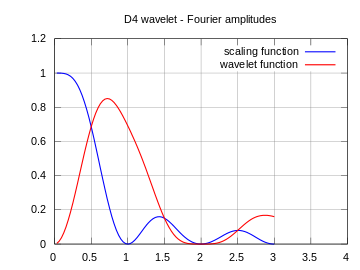
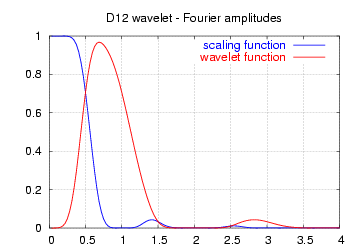
| Amplitudes dos espectros de frequência das funções acima |
|
|

|
Observe que os espectros mostrados aqui não são a resposta de frequência dos filtros passa-alta e passa-baixa, mas sim as amplitudes das transformadas Fourier contínuas das funções de escala (azul) e wavelet (vermelho).
Wavelets ortogonais de Daubechies D2 – D20 resp. db1 – db10 são comumente usados. O número do índice refere-se ao número N de coeficientes. Cada wavelet tem um número de momentos zero ou momentos de fuga igual à metade do número de coeficientes. Por exemplo, D2 tem um momento de fuga, D4 tem dois, etc. Um momento de fuga limita a capacidade das wavelets de representar comportamento polinomial ou informação em um sinal. Por exemplo, D2, com um momento de fuga, codifica facilmente polinômios de um coeficiente ou componentes de sinal constantes. D4 codifica polinômios com dois coeficientes, isto é, componentes de sinal constantes e lineares; e D6 codifica 3 polinômios, isto é, componentes de sinal constantes, lineares e quadráticas . Essa capacidade de codificar sinais está, no entanto, sujeita ao fenômeno de vazamento de escala e à falta de invariância ao deslocamento, que surgem da operação de deslocamento discreto (abaixo) durante a aplicação da transformada. As sub-sequências que representam componentes de sinal lineares, quadráticos (por exemplo) são tratadas de maneira diferente pela transformação, dependendo se os pontos se alinham com localizações de números pares ou ímpares na sequência. A falta da propriedade importante de invariância ao deslocamento levou ao desenvolvimento de várias versões diferentes de uma transformada wavelet invariante ao deslocamento (discreta) .
Construção
Tanto a sequência de escala (filtro passa-baixa) e a sequência wavelet (filtro passa-banda) (ver wavelet ortogonal para detalhes desta construção) serão normalizadas aqui para ter soma igual a 2 e soma dos quadrados igual a 2. Em algumas aplicações, eles são normalizados para ter soma , de modo que ambas as sequências e todos os deslocamentos deles por um número par de coeficientes são ortonormais entre si.
Usando a representação geral para uma sequência de escala de uma transformada wavelet discreta ortogonal com ordem de aproximação A ,
com N = 2 A , p tendo coeficientes reais, p (1) = 1 e deg ( p ) = A - 1, pode-se escrever a condição de ortogonalidade como
ou igualmente como
com o polinômio de Laurent
gerando todas as sequências simétricas e , além disso, P ( X ) representa o polinômio Laurent simétrico
Desde a
P assume valores não negativos no segmento [0,2].
A equação (*) tem uma solução mínima para cada A , que pode ser obtida pela divisão no anel da série de potências truncada em X ,
Obviamente, isso tem valores positivos em (0,2).
A equação homogênea para (*) é anti-simétrica em relação a X = 1 e tem, portanto, a solução geral
com R algum polinômio com coeficientes reais. Essa é a soma
deve ser não negativo no intervalo [0,2] traduz em um conjunto de restrições lineares sobre os coeficientes de R . Os valores de P no intervalo [0,2] são limitados por alguma quantidade que maximiza r resultados em um programa linear com infinitas condições de desigualdade.
Resolver
para p, usa-se uma técnica chamada fatoração espectral resp. Algoritmo de Fejér-Riesz. O polinômio P ( X ) se divide em fatores lineares
Cada fator linear representa um polinômio de Laurent
que pode ser fatorado em dois fatores lineares. Pode-se atribuir qualquer um dos dois fatores lineares a p ( Z ), obtendo-se 2 N soluções possíveis. Para a fase extrema, escolhe-se aquele que tem todas as raízes complexas de p ( Z ) dentro ou no círculo unitário e, portanto, é real.
Para a transformada wavelet de Daubechies, um par de filtros lineares é usado. Cada filtro do par deve ser um filtro de espelho de quadratura . Resolver o coeficiente do filtro linear usando a propriedade de filtro de espelho de quadratura resulta na seguinte solução para os valores de coeficiente para filtro de ordem 4.
As sequências de escala de ordem de aproximação mais baixa
Abaixo estão os coeficientes para as funções de escala para D2-20. Os coeficientes wavelet são derivados invertendo a ordem dos coeficientes da função de escala e, em seguida, invertendo o sinal de cada um dos segundos, (ou seja, wavelet D4 {−0,1830127, −0,3169873, 1,1830127, −0,6830127}). Matematicamente, esta parece ser onde k é o dice de coeficiente, b é um coeficiente da sequência de onda e um coeficiente da sequência de escala. N é o índice wavelet, ou seja, 2 para D2.
| D2 ( Haar ) | D4 | D6 | D8 | D10 | D12 | D14 | D16 | D18 | D20 |
|---|---|---|---|---|---|---|---|---|---|
| 1 | 0,6830127 | 0,47046721 | 0,32580343 | 0,22641898 | 0,15774243 | 0,11009943 | 0,07695562 | 0,05385035 | 0,03771716 |
| 1 | 1,1830127 | 1,14111692 | 1.01094572 | 0,85394354 | 0,69950381 | 0,56079128 | 0,44246725 | 0,34483430 | 0,26612218 |
| 0,3169873 | 0,650365 | 0,89220014 | 1.02432694 | 1.06226376 | 1.03114849 | 0,95548615 | 0,85534906 | 0,74557507 | |
| -0,1830127 | -0,19093442 | -0,03957503 | 0,19576696 | 0,44583132 | 0,66437248 | 0,82781653 | 0,92954571 | 0,97362811 | |
| -0,12083221 | -0,26450717 | -0,34265671 | -0,31998660 | -0.20351382 | -0,02238574 | 0,18836955 | 0,39763774 | ||
| 0,0498175 | 0,0436163 | -0,04560113 | -0,18351806 | -0,31683501 | -0,40165863 | -0,41475176 | -0,35333620 | ||
| 0,0465036 | 0,10970265 | 0,13788809 | 0,1008467 | 6,68194092 × 10 −4 | -0,13695355 | -0,27710988 | |||
| -0,01498699 | -0,00882680 | 0,03892321 | 0,11400345 | 0,18207636 | 0,21006834 | 0,18012745 | |||
| -0,01779187 | -0,04466375 | -0,05378245 | -0,02456390 | 0,043452675 | 0,13160299 | ||||
| 4,71742793 × 10 −3 | 7,83251152 × 10 −4 | -0,02343994 | -0,06235021 | -0,09564726 | -0,10096657 | ||||
| 6,75606236 × 10 −3 | 0,01774979 | 0,01977216 | 3,54892813 × 10 −4 | -0,04165925 | |||||
| −1,52353381 × 10 −3 | 6,07514995 × 10 −4 | 0,01236884 | 0,03162417 | 0,04696981 | |||||
| −2,54790472 × 10 −3 | −6,88771926 × 10 −3 | −6,67962023 × 10 −3 | 5.10043697 × 10 −3 | ||||||
| 5,00226853 × 10 −4 | −5,54004549 × 10 −4 | −6,05496058 × 10 −3 | -0,01517900 | ||||||
| 9,55229711 × 10 −4 | 2,61296728 × 10 −3 | 1,97332536 × 10 −3 | |||||||
| −1,66137261 × 10 −4 | 3,25814671 × 10 −4 | 2,81768659 × 10 −3 | |||||||
| −3,56329759 × 10 −4 | −9,69947840 × 10 −4 | ||||||||
| 5,5645514 × 10 −5 | −1,64709006 × 10 −4 | ||||||||
| 1,32354367 × 10 −4 | |||||||||
| −1,875841 × 10 −5 |
Partes da construção também são usadas para derivar as ondas de Cohen – Daubechies – Feauveau (CDFs) bi-ortogonais .
Implementação
Embora softwares como o Mathematica suportem wavelets Daubechies diretamente, uma implementação básica é possível no MATLAB (neste caso, Daubechies 4). Esta implementação usa periodização para lidar com o problema de sinais de comprimento finito. Outros métodos mais sofisticados estão disponíveis, mas muitas vezes não é necessário usá-los, pois afeta apenas as extremidades do sinal transformado. A periodização é realizada na transformação direta diretamente na notação vetorial MATLAB e na transformação inversa usando a circshift()função:
Transformar, D4
Assume-se que S , um vetor coluna com um número par de elementos, foi pré-definido como o sinal a ser analisado. Observe que os coeficientes D4 são [1 + √ 3 , 3 + √ 3 , 3 - √ 3 , 1 - √ 3 ] / 4.
N = length(S);
s1 = S(1:2:N - 1) + sqrt(3) * S(2:2:N);
d1 = S(2:2:N) - sqrt(3) / 4 * s1 - (sqrt(3) - 2) / 4 * [s1(N / 2); s1(1:N / 2 - 1)];
s2 = s1 - [d1(2:N / 2); d1(1)];
s = (sqrt(3) - 1) / sqrt(2) * s2;
d = - (sqrt(3) + 1) / sqrt(2) * d1;
Transformada inversa, D4
d1 = d * ((sqrt(3) - 1) / sqrt(2));
s2 = s * ((sqrt(3) + 1) / sqrt(2));
s1 = s2 + circshift(d1, - 1);
S(2:2:N) = d1 + sqrt(3) / 4 * s1 + (sqrt(3) - 2) / 4 * circshift(s1, 1);
S(1:2:N - 1) = s1 - sqrt(3) * S(2:2:N);
Binomial-QMF
Foi mostrado por Ali Akansu em 1990 que o banco de filtro de espelho de quadratura binomial (QMF binomial) é idêntico ao filtro wavelet de Daubechies, e seu desempenho foi classificado entre as soluções de subespaço conhecidas de uma perspectiva de processamento de sinal em tempo discreto. Foi uma extensão do trabalho anterior sobre coeficiente binomial e polinômios de Hermite que levou ao desenvolvimento da Transformação Hermite modificada (MHT) em 1987. As funções quadradas de magnitude dos filtros Binomial-QMF são mostradas como sendo as funções únicas maximamente planas em um formulação de projeto de reconstrução perfeita de duas bandas QMF (PR-QMF) que está relacionada à regularidade da wavelet no domínio contínuo.
Veja também
Referências
links externos
- Ingrid Daubechies: Ten Lectures on Wavelets , SIAM 1992.
- Proc. 1º Simpósio da NJIT sobre Wavelets, Subbands and Transforms, abril de 1990.
- Akansu, Ali N .; Haddad, Richard A. (1992), Multiresolution Signal Decomposition: Transforms, Subbands, and Wavelets , Boston, MA: Academic Press, ISBN 978-0-12-047141-6
- AN Akansu, Filter Banks and Wavelets in Signal Processing: A Critical Review , Proc. SPIE Video Communications and PACS for Medical Applications (Invited Paper), pp. 330-341, vol. 1977, Berlim, outubro de 1993.
- Carlos Cabrelli, Ursula Molter : "Generalized Self-similarity", Journal of Mathematical Analysis and Applications , 230: 251–260, 1999.
- Implementação de hardware de wavelets
- "Daubechies wavelets" , Encyclopedia of Mathematics , EMS Press , 2001 [1994].
- I. Kaplan, The Daubechies D4 Wavelet Transform .
- Jensen; la Cour-Harbo (2001). Ripples in Mathematics . Berlim: Springer. pp. 157–160. ISBN 3-540-41662-5.
- Jianhong (Jackie) Shen e Gilbert Strang , Applied and Computational Harmonic Analysis , 5 (3), Asymptotics of Daubechies Filters, Scaling Functions, and Wavelets .





















