Estrutura distributiva - Distributive lattice

Em matemática , uma rede distributiva é uma rede na qual as operações de junção e reunião se distribuem umas sobre as outras. Os exemplos prototípicos de tais estruturas são coleções de conjuntos para os quais as operações de rede podem ser fornecidas por união e interseção de conjuntos . Na verdade, essas redes de conjuntos descrevem o cenário completamente: toda rede distributiva é - até o isomorfismo - dada como tal rede de conjuntos.

Definição

Como no caso de redes arbitrárias, pode-se escolher considerar uma rede distributiva L como uma estrutura da teoria da ordem ou como álgebra universal . Ambas as visões e sua correspondência mútua são discutidas no artigo sobre redes . Na situação atual, a descrição algébrica parece ser mais conveniente:

Uma rede ( L , ∨, ∧) é distributiva se a seguinte identidade adicional for válida para todos os x , y e z em L :

x ∧ ( y ∨ z ) = ( x ∧ y ) ∨ ( x ∧ z ).

Visualizando reticulados como conjuntos parcialmente ordenados, isso diz que a operação meet preserva junções finitas não vazias. É um fato básico da teoria da rede que a condição acima é equivalente ao seu dual :

x ∨ ( y ∧ z ) = ( x ∨ y ) ∧ ( x ∨ z ) para todos os x , y , e z em L .

Em cada rede, definindo p ≤ q como de costume para significar p ∧ q = p , a desigualdade x ∧ ( y ∨ z ) ≥ ( x ∧ y ) ∨ ( x ∧ z ) se mantém, bem como sua desigualdade dual x ∨ ( y ∧ z ) ≤ ( x ∨ y ) ∧ ( x ∨ z ). Uma rede é distributiva se uma das desigualdades inversas também for válida. Mais informações sobre a relação dessa condição com outras condições de distributividade da teoria da ordem podem ser encontradas no artigo sobre distributividade (teoria da ordem) .

Morfismos

Um morfismo de redes distributivas é apenas um homomorfismo de rede como dado no artigo sobre redes , ou seja, uma função que é compatível com as duas operações de rede. Como tal morfismo de redes preserva a estrutura da rede, conseqüentemente também preservará a distributividade (e, portanto, será um morfismo de redes distributivas).

Exemplos

Malha de Young

As redes distributivas são onipresentes, mas também estruturas bastante específicas. Como já mencionado, o principal exemplo de redes distributivas são redes de conjuntos, onde junção e encontro são dados pelas operações teóricas de conjuntos usuais. Outros exemplos incluem:

• A álgebra de Lindenbaum da maioria das lógicas que suportam conjunção e disjunção é uma rede distributiva, ou seja, "e" distribui "ou" e vice-versa.
• Cada álgebra booleana é uma rede distributiva.
• Cada álgebra de Heyting é uma rede distributiva. Especialmente isso inclui todos os locais e, portanto, todas as redes de conjuntos abertos de espaços topológicos . Observe também que as álgebras de Heyting podem ser vistas como álgebras de Lindenbaum da lógica intuicionista , o que as torna um caso especial do primeiro exemplo.
• Cada conjunto totalmente ordenado é uma rede distributiva com max como join e min como meet.
• Os números naturais formam uma rede distributiva (condicionalmente completa) tomando o maior divisor comum como encontro e o mínimo múltiplo comum como junção. Essa rede também tem um elemento mínimo, ou seja, 1, que, portanto, serve como o elemento de identidade para as junções.
• Dado um número inteiro positivo n , o conjunto de todos os divisores positivos de n forma uma rede distributiva, novamente com o maior divisor comum como encontro e o mínimo múltiplo comum como junção. Esta é uma álgebra booleana se e somente se n for livre de quadrados .
• Um espaço vetorial ordenado por rede é uma rede distributiva.
• A rede de Young dada pela ordem de inclusão dos diagramas de Young representando partições inteiras é uma rede distributiva.
• Os pontos de um politopo distributivo (um politopo convexo fechado sob as operações mínimo e máximo coordenado), com essas duas operações como as operações de junção e encontro da rede.

No início do desenvolvimento da teoria da rede, Charles S. Peirce acreditava que todas as redes são distributivas, ou seja, a distributividade segue do resto dos axiomas da rede. No entanto, as provas de independência foram fornecidas por Schröder , Voigt, ^{( de )} Lüroth , Korselt e Dedekind .

Propriedades características

Existem várias formulações equivalentes à definição acima. Por exemplo, L é distributivo se e somente se o seguinte for válido para todos os elementos x , y , z em L :

( x y ) ( y z ) ( z x ) = ( x y ) ( y z ) ( z x ).${\ displaystyle \ wedge}$${\ displaystyle \ vee}$${\ displaystyle \ wedge}$${\ displaystyle \ vee}$${\ displaystyle \ wedge}$${\ displaystyle \ vee}$${\ displaystyle \ wedge}$${\ displaystyle \ vee}$${\ displaystyle \ wedge}$${\ displaystyle \ vee}$

Da mesma forma, L é distributivo se e somente se

x z = y z e x z = y z sempre implicam x = y .${\ displaystyle \ wedge}$${\ displaystyle \ wedge}$${\ displaystyle \ vee}$${\ displaystyle \ vee}$

• Diagramas de Hasse das duas redes prototípicas não distributivas
• 

  A rede de diamante M ₃ não é distributiva: x ∧ ( y ∨ z ) = x ∧ 1 = x ≠ 0 = 0 ∨ 0 = ( x ∧ y ) ∨ ( x ∧ z ) .

• 

  A rede do pentágono N ₅ não é distributiva: x ∧ ( y ∨ z ) = x ∧ 1 = x ≠ z = 0 ∨ z = ( x ∧ y ) ∨ ( x ∧ z ) .

Treliça distributiva que contém N5 (linhas a cheio, para a esquerda) e M3 (direita) como sub- conjunto , mas não como sub rede

As redes não distributivas mais simples são M ₃ , a "rede do diamante", e N ₅ , a "rede do pentágono". Uma rede é distributiva se e somente se nenhuma de suas sub-redes é isomórfica a M ₃ ou  N ₅ ; uma sub-rede é um subconjunto que é fechado nas operações de encontro e junção da rede original. Observe que isso não é o mesmo que ser um subconjunto que é uma rede sob a ordem original (mas possivelmente com diferentes operações de junção e reunião). Outras caracterizações derivam da teoria da representação na próxima seção.

Uma maneira alternativa de afirmar o mesmo fato é que toda rede distributiva é um produto subdireto de cópias da cadeia de dois elementos , ou que o único membro subdiretamente irredutível da classe de redes distributivas é a cadeia de dois elementos. Como corolário, toda rede booleana também possui essa propriedade.

Finalmente, a distributividade envolve várias outras propriedades agradáveis. Por exemplo, um elemento de uma rede distributiva é atender primo se e somente se for irredutível ao encontro , embora o último seja em geral uma propriedade mais fraca. Por dualidade, o mesmo é verdadeiro para elementos join-prime e join-irredutível . Se uma rede é distributiva, sua relação de cobertura forma um gráfico mediano .

Além disso, toda rede distributiva também é modular .

Teoria da representação

A introdução já sugeriu a caracterização mais importante para redes distributivas: uma rede é distributiva se e somente se for isomórfica a uma rede de conjuntos (fechada sob a união e interseção de conjuntos ). (A última estrutura é às vezes chamada de anel de conjuntos neste contexto.) Que a união e a interseção do conjunto sejam de fato distributivas no sentido acima é um fato elementar. A outra direção é menos trivial, pois requer os teoremas de representação declarados abaixo. O insight importante dessa caracterização é que as identidades (equações) que se mantêm em todas as redes distributivas são exatamente aquelas que se sustentam em todas as redes de conjuntos no sentido acima.

O teorema de representação de Birkhoff para redes distributivas afirma que toda rede distributiva finita é isomórfica à rede de conjuntos inferiores do poset de seus elementos primos de junção (equivalentemente: irredutíveis de junção). Isso estabelece uma bijeção (até isomorfismo ) entre a classe de todos os posets finitos e a classe de todas as redes distributivas finitas. Esta bijeção pode ser estendida a uma dualidade de categorias entre homomorfismos de redes distributivas finitas e funções monótonas de posets finitos. Generalizar esse resultado para redes infinitas, no entanto, requer a adição de mais estrutura.

Outro teorema da representação inicial é agora conhecido como teorema da representação de Stone para redes distributivas (o nome homenageia Marshall Harvey Stone , que o provou pela primeira vez). Ele caracteriza as redes distributivas como as redes de conjuntos abertos compactos de certos espaços topológicos . Este resultado pode ser visto como uma generalização do famoso teorema da representação de Stone para álgebras booleanas e como uma especialização da configuração geral da dualidade de Stone .

Uma outra representação importante foi estabelecida por Hilary Priestley em seu teorema de representação para redes distributivas . Nesta formulação, uma rede distributiva é usada para construir um espaço topológico com uma ordem parcial adicional em seus pontos, produzindo um espaço de Stone ordenado (completamente separado por ordem) (ou espaço de Priestley ). A treliça original é recuperada como a coleção de conjuntos inferiores clopen deste espaço.

Como consequência dos teoremas de Stone e Priestley, pode-se ver facilmente que qualquer rede distributiva é realmente isomórfica a uma rede de conjuntos. No entanto, as provas de ambas as afirmações requerem o teorema do ideal primo Booleano , uma forma fraca do axioma da escolha .

Redes distributivas gratuitas

Redes distributivas livres em geradores zero, um, dois e três. Os elementos rotulados como "0" e "1" são a junção e reunião vazias, e o elemento rotulado como "maioria" é ( x ∧ y ) ∨ ( x ∧ z ) ∨ ( y ∧ z ) = ( x ∨ y ) ∧ ( x ∨ z ) ∧ ( y ∨ z ).

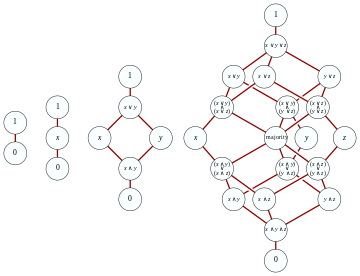
A rede distributiva livre sobre um conjunto de geradores G pode ser construída muito mais facilmente do que uma rede livre geral. A primeira observação é que, usando as leis da distributividade, todo termo formado pelas operações binárias e em um conjunto de geradores pode ser transformado na seguinte forma normal equivalente : ${\ displaystyle \ lor}$${\ displaystyle \ land}$

${\ displaystyle M_ {1} \ lor M_ {2} \ lor \ cdots \ lor M_ {n},}$

onde são finitas encontra de elementos de L . Além disso, uma vez que ambos Meet e Join são associativos , comutativos e idempotentes , pode-se ignorar duplicatas e ordem, e representar uma junção de encontros como o acima como um conjunto de conjuntos: ${\ displaystyle M_ {i}}$

${\ displaystyle \ {N_ {1}, N_ {2}, \ ldots, N_ {n} \},}$

onde o são subconjuntos finitos de L . No entanto, ainda é possível que dois desses termos denotem o mesmo elemento da rede distributiva. Isso ocorre quando há índices j e k tais que são um subconjunto de. Nesse caso, o encontro de será abaixo do encontro de e, portanto, pode-se remover com segurança o conjunto redundante sem alterar a interpretação de todo o termo. Consequentemente, um conjunto de subconjuntos finitos de G será chamado de irredundante sempre que todos os seus elementos forem mutuamente incomparáveis ​​(com relação à ordenação do subconjunto); isto é, quando forma uma anticadeia de conjuntos finitos . ${\ displaystyle N_ {i}}$${\ displaystyle N_ {j}}$${\ displaystyle N_ {k}.}$${\ displaystyle N_ {k}}$${\ displaystyle N_ {j},}$${\ displaystyle N_ {k}}$${\ displaystyle N_ {i}}$

Agora, a rede de distribuição livre ao longo de um conjunto de geradores G é definido no conjunto de todos os conjuntos de redundâncias finitos de subconjuntos finitos de G . A junção de dois conjuntos irredundantes finitos é obtida a partir de sua união removendo todos os conjuntos redundantes. Da mesma forma, o encontro de dois conjuntos S e T é a versão irredundante de A verificação de que essa estrutura é uma rede distributiva com a propriedade universal necessária é rotineira. ${\ displaystyle \ {N \ cup M \ mid N \ in S, M \ in T \}.}$

O número de elementos em redes distributivas livres com n geradores é dado pelos números de Dedekind . Esses números crescem rapidamente e são conhecidos apenas por n  ≤ 8; eles são

2, 3, 6, 20, 168, 7581, 7828354, 2414682040998, 56130437228687557907788 (sequência A000372 no OEIS ).

Os números acima contam o número de elementos em redes distributivas livres nas quais as operações de rede são junções e encontros de conjuntos finitos de elementos, incluindo o conjunto vazio. Se junções vazias e encontros vazios não forem permitidos, as redes distributivas livres resultantes terão dois elementos a menos; seus números de elementos formam a sequência

0, 1, 4, 18, 166, 7579, 7828352, 2414682040996, 56130437228687557907786 (sequência A007153 no OEIS ).

Veja também

• Estrutura totalmente distributiva - uma estrutura na qual junções infinitas distribuem-se por encontros infinitos
• Teoria da dualidade para redes distributivas
• Espaço espectral

Referências

Leitura adicional

• Burris, Stanley N .; Sankappanavar, HP (1981). Um Curso de Álgebra Universal . Springer-Verlag. ISBN 3-540-90578-2.
• Sequência OEIS A006982 (Número de redes distributivas não rotuladas com n elementos)