Variável fictícia (estatísticas) - Dummy variable (statistics)

Em estatística e econometria , particularmente em análise de regressão , uma variável dummy é aquela que assume apenas o valor 0 ou 1 para indicar a ausência ou presença de algum efeito categórico que pode ser esperado para alterar o resultado. Eles podem ser considerados como substitutos numéricos para fatos qualitativos em um modelo de regressão , classificando os dados em categorias mutuamente exclusivas (como fumante e não fumante).

Uma variável independente fictícia (também chamada de variável explicativa fictícia) que para alguma observação tem um valor de 0 fará com que o coeficiente dessa variável não tenha nenhum papel em influenciar a variável dependente , enquanto quando a dummy assume um valor 1, seu coeficiente age para alterar a interceptação . Por exemplo, suponha que pertencer a um grupo seja uma das variáveis ​​qualitativas relevantes para uma regressão. Se a associação ao grupo for arbitrariamente atribuída ao valor 1, então todos os outros obterão o valor 0. Então a interceptação seria o termo constante para não-membros, mas seria o termo constante mais o coeficiente da dummy de associação no caso do grupo membros.

Variáveis ​​fictícias são usadas frequentemente em análises de séries temporais com mudança de regime, análise sazonal e aplicações de dados qualitativos.

Incorporando um manequim independente

Figura 1: Gráfico mostrando salário = α ₀ + δ ₀ mulheres + α ₁ educação + U , δ ₀  <0.

As variáveis ​​fictícias são incorporadas da mesma forma que as variáveis ​​quantitativas (como variáveis ​​explicativas) nos modelos de regressão. Por exemplo, se considerarmos um modelo de regressão do tipo Mincer de determinação de salários, em que os salários dependem do gênero (qualitativo) e dos anos de educação (quantitativo):

${\ displaystyle \ ln {\ text {wage}} = \ alpha _ {0} + \ delta _ {0} {\ text {female}} + \ alpha _ {1} {\ text {educação}} + u}$

onde está o termo de erro . No modelo, feminino = 1 quando a pessoa é do sexo feminino e feminino = 0 quando a pessoa é do sexo masculino. pode ser interpretado como a diferença de salários entre mulheres e homens, mantendo a educação constante. Assim, δ ₀ ajuda a determinar se há discriminação de salários entre homens e mulheres. Por exemplo, se δ ₀ > 0 (coeficiente positivo), então as mulheres ganham um salário mais alto do que os homens (mantendo os outros fatores constantes). Os coeficientes associados às variáveis ​​dummy são chamados de coeficientes de interceptação diferencial . O modelo pode ser representado graficamente como uma mudança de interceptação entre mulheres e homens. Na figura, é mostrado o caso δ ₀ <0 (em que os homens ganham um salário mais alto do que as mulheres). ${\ displaystyle u \ sim N (0, \ sigma ^ {2})}$${\ displaystyle \ delta _ {0}}$

Variáveis ​​fictícias podem ser estendidas para casos mais complexos. Por exemplo, os efeitos sazonais podem ser capturados criando variáveis ​​fictícias para cada uma das estações: se a observação for para o verão, e igual a zero caso contrário; se e somente se outono, caso contrário, é igual a zero; se e somente se inverno, caso contrário, é igual a zero; e se e somente se primavera, caso contrário, é igual a zero. Nos dados em painel , dummies estimadoras de efeitos fixos são criadas para cada uma das unidades em dados transversais (por exemplo, empresas ou países) ou períodos em uma série temporal combinada. No entanto, em tais regressões, o termo constante deve ser removido ou uma das dummies deve ser removida, com sua categoria associada se tornando a categoria base contra a qual as outras são avaliadas a fim de evitar a armadilha da variável dummy : ${\ displaystyle D_ {1} = 1}$${\ displaystyle D_ {2} = 1}$${\ displaystyle D_ {3} = 1}$${\ displaystyle D_ {4} = 1}$

O termo constante em todas as equações de regressão é um coeficiente multiplicado por um regressor igual a um. Quando a regressão é expressa como uma equação matricial, a matriz dos regressores consiste em uma coluna de uns (o termo constante), vetores de zeros e uns (os dummies) e possivelmente outros regressores. Se incluirmos manequins masculinos e femininos, digamos, a soma desses vetores é um vetor de uns, uma vez que toda observação é categorizada como masculina ou feminina. Essa soma é, portanto, igual ao regressor do termo constante, o primeiro vetor de uns. Como resultado, a equação de regressão não terá solução, mesmo pelo método pseudoinverso típico. Em outras palavras: se o regressor vetor de uns (termo constante) e um conjunto exaustivo de dummies estão presentes, ocorre multicolinearidade perfeita , e o sistema de equações formado pela regressão não tem uma solução única. Isso é conhecido como armadilha de variável fictícia . A armadilha pode ser evitada removendo o termo constante ou um dos bonecos ofensivos. A dummy removida então se torna a categoria base com a qual as outras categorias são comparadas.

Modelos ANOVA

Um modelo de regressão no qual a variável dependente é quantitativa por natureza, mas todas as variáveis ​​explicativas são dummies (qualitativa por natureza) é chamado de modelo de Análise de Variância (ANOVA).

Modelo ANOVA com uma variável qualitativa

Suponha que queremos executar uma regressão para descobrir se o salário médio anual dos professores de escolas públicas difere entre três regiões geográficas no País A com 51 estados: (1) Norte (21 estados) (2) Sul (17 estados) (3) Oeste (13 estados). Digamos que os salários médios aritméticos simples sejam os seguintes: $ 24.424,14 (Norte), $ 22.894 (Sul), $ 26.158,62 (Oeste). As médias aritméticas são diferentes, mas são estatisticamente diferentes umas das outras? Para comparar os valores médios, podem ser utilizadas técnicas de Análise de Variância . O modelo de regressão pode ser definido como:

${\ displaystyle Y_ {i} = \ alpha _ {1} + \ alpha _ {2} D_ {2i} + \ alpha _ {3} D_ {3i} + u_ {i}}$ ,

Onde

${\ displaystyle Y_ {i} =}$ salário médio anual de professores de escolas públicas no estado i

${\ displaystyle D_ {2i} = 1}$ se o estado i fica na Região Norte

${\ displaystyle D_ {2i} = 0}$ caso contrário (qualquer região diferente do Norte)

${\ displaystyle D_ {3i} = 1}$ se o estado i está na região sul

${\ displaystyle D_ {3i} = 0}$ de outra forma

Neste modelo, temos apenas regressores qualitativos, assumindo o valor 1 se a observação pertencer a uma categoria específica e 0 se pertencer a qualquer outra categoria. Isso o torna um modelo ANOVA.

Figura 2: Gráfico mostrando os resultados da regressão do exemplo do modelo ANOVA: Salários médios anuais de professores de escolas públicas em 3 regiões do País A.

Agora, tomando a expectativa de ambos os lados, obtemos o seguinte:

Salário médio dos professores de escolas públicas da Região Norte:

E ( Y _i | D _{2 i} = 1, D _{3 i} = 0) = α ₁ + α ₂

Salário médio dos professores de escolas públicas da Região Sul:

E (Y _i | D _2i = 0, D _3i = 1) = α ₁ + α ₃

Salário médio dos professores da rede pública da Região Oeste:

E (Y _i | D _2i = 0, D _3i = 0) = α ₁

(O termo de erro não é incluído nos valores esperados, pois é assumido que ele satisfaz as condições OLS usuais , ou seja, E (u _i ) = 0)

Os valores esperados podem ser interpretados da seguinte forma: O salário médio dos professores de escolas públicas no Ocidente é igual ao termo de interceptação α ₁ na equação de regressão múltipla e os coeficientes de interceptação diferencial, α ₂ e α ₃ , explicam por quanto a média os salários dos professores nas Regiões Norte e Sul variam em relação aos professores do Oeste. Assim, os salários médios dos professores do Norte e do Sul são comparados com os salários médios dos professores do Oeste. Assim, a Região Oeste torna-se o grupo de base ou o grupo de referência , ou seja, o grupo contra o qual as comparações são feitas. A categoria omitida , ou seja, a categoria à qual nenhuma dummy é atribuída, é considerada a categoria do grupo de base.

Usando os dados fornecidos, o resultado da regressão seria:

Ŷ _i = 26,158,62 - 1734,473D _{2 i} - 3264,615D _{3 i}

se = (1128.523) (1435.953) (1499.615)

t = (23,1759) (-1,2078) (-2,1776)

p = (0,0000) (0,2330) (0,0349)

R ² = 0,0901

onde, se = erro padrão , t = t-estatísticas , p = valor de p

O resultado da regressão pode ser interpretado como: O salário médio dos professores no Oeste (grupo de base) é cerca de $ 26.158, o salário dos professores no Norte é inferior em cerca de $ 1.734 ($ 26.158,62 - $ 1734,473 = $ 24.424,14, que é o salário médio dos professores no Norte) e o dos professores no Sul é inferior em cerca de $ 3.265 ($ 26.158,62 - $ 3.264.615 = $ 22.894, que é o salário médio dos professores no Sul).

Para saber se os salários médios dos professores do Norte e do Sul são estatisticamente diferentes dos salários dos professores do Oeste (a categoria de comparação), temos de descobrir se os coeficientes de inclinação do resultado da regressão são estatisticamente significativos . Para isso, precisamos considerar os valores de p . O coeficiente de inclinação estimado para o Norte não é estatisticamente significativo, pois seu valor de p é 23 por cento; no entanto, o do Sul é estatisticamente significativo no nível de 5%, pois seu valor de p é de apenas cerca de 3,5%. Assim, o resultado geral é que os salários médios dos professores no Oeste e no Norte não são estatisticamente diferentes uns dos outros, mas o salário médio dos professores no Sul é estatisticamente inferior ao do Oeste em cerca de $ 3.265. O modelo é mostrado em diagrama na Figura 2. Este modelo é um modelo ANOVA com uma variável qualitativa com 3 categorias.

Modelo ANOVA com duas variáveis ​​qualitativas

Suponha que consideremos um modelo ANOVA com duas variáveis ​​qualitativas, cada uma com duas categorias: Salários por hora devem ser explicados em termos das variáveis ​​qualitativas Estado Civil (Casado / Solteiro) e Região Geográfica (Norte / Não Norte). Aqui, o estado civil e a região geográfica são as duas variáveis ​​fictícias explicativas.

Digamos que o resultado da regressão com base em alguns dados fornecidos seja o seguinte:

Ŷ _i = 8,8148 + 1,0997D ₂ - 1,6729D ₃

Onde,

Y = salários por hora (em $)

D ₂ = estado civil, 1 = casado, 0 = caso contrário

D ₃ = região geográfica, 1 = Norte, 0 = caso contrário

Nesse modelo, uma única dummy é atribuída a cada variável qualitativa, uma a menos que o número de categorias incluídas em cada uma.

Aqui, o grupo de base é a categoria omitida: Solteiro, região Não Norte (Solteiros que não moram na região Norte). Todas as comparações seriam feitas em relação a este grupo de base ou categoria omitida. O salário médio por hora na categoria de base é de cerca de US $ 8,81 (prazo interceptado). Em comparação, o salário médio por hora dos casados ​​é maior em cerca de $ 1,10 e é igual a cerca de $ 9,91 ($ 8,81 + $ 1,10). Em contraste, o salário médio por hora daqueles que vivem no Norte é inferior em cerca de $ 1,67 e é de cerca de $ 7,14 ($ 8,81 - $ 1,67).

Assim, se mais de uma variável qualitativa for incluída na regressão, é importante observar que a categoria omitida deve ser escolhida como a categoria de benchmark e todas as comparações serão feitas em relação a essa categoria. O termo de interceptação mostrará a expectativa da categoria de benchmark e os coeficientes de inclinação mostrarão o quanto as outras categorias diferem da categoria de benchmark (omitida).

Modelos ANCOVA

Um modelo de regressão que contém uma mistura de variáveis ​​quantitativas e qualitativas é chamado de modelo de Análise de Covariância (ANCOVA). Os modelos ANCOVA são extensões dos modelos ANOVA. Eles controlam estatisticamente os efeitos das variáveis ​​explicativas quantitativas (também chamadas de covariáveis ​​ou variáveis ​​de controle).

Para ilustrar como os regressores qualitativos e quantitativos são incluídos para formar modelos ANCOVA, suponha que consideremos o mesmo exemplo usado no modelo ANOVA com uma variável qualitativa: salário médio anual de professores de escolas públicas em três regiões geográficas do País A. Se incluirmos um quantitativo variável, gasto do Governo do Estado com escolas públicas por aluno , nesta regressão, temos o seguinte modelo:

Figura 3: Gráfico que mostra os resultados da regressão do exemplo do modelo ANCOVA: Salário (Y) do professor da escola pública em relação ao gasto do Estado por aluno nas escolas públicas.

Y _i = α ₁ + α ₂ D _2i + α ₃ D _3i + α ₄ X _i + U _i

Onde,

Y _i = salário médio anual de professores de escolas públicas no estado i

X _i = despesas do Estado em escolas públicas por aluno

D _2i = 1, se o Estado i estiver na Região Norte

D _2i = 0, caso contrário

D _3i = 1, se o Estado i estiver na Região Sul

D _3i = 0, caso contrário

Digamos que a saída de regressão para este modelo seja

Ŷ _i = 13.269,11 - 1673,514D _2i - 1144,157D _3i + 3,2889X _i

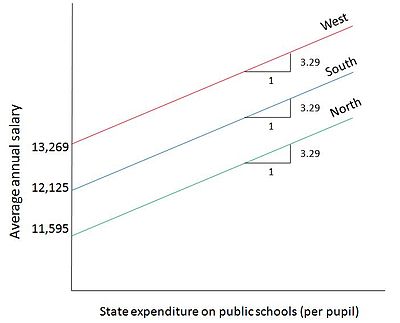
O resultado sugere que, para cada US $ 1 de aumento nos gastos do Estado por aluno nas escolas públicas, o salário médio de um professor de escola pública aumenta cerca de US $ 3,29. Além disso, para um estado da região Norte, o salário médio dos professores é inferior ao da região Oeste em cerca de US $ 1.673 e para um estado da região Sul, o salário médio dos professores é inferior ao da região Oeste em cerca de $ 1144. A Figura 3 mostra esse modelo em diagrama. As linhas salariais médias são paralelas entre si pela suposição do modelo de que o coeficiente de despesas não varia por estado. O trade off mostrado separadamente no gráfico para cada categoria é entre as duas variáveis ​​quantitativas: salários dos professores das escolas públicas (Y) em relação aos gastos do Estado por aluno nas escolas públicas (X).

Interações entre variáveis ​​dummy

Os regressores quantitativos em modelos de regressão costumam interagir uns com os outros. Da mesma forma, regressores qualitativos, ou dummies, também podem ter efeitos de interação entre si, e essas interações podem ser representadas no modelo de regressão. Por exemplo, em uma regressão envolvendo determinação de salários, se duas variáveis ​​qualitativas forem consideradas, a saber, sexo e estado civil, pode haver uma interação entre estado civil e sexo. Essas interações podem ser mostradas na equação de regressão, conforme ilustrado pelo exemplo abaixo.

Com as duas variáveis ​​qualitativas sendo gênero e estado civil e com o explicador quantitativo sendo anos de escolaridade, uma regressão que é puramente linear nos explicadores seria

Y _i = β ₁ + β ₂ D _{2, i} + β ₃ D _{3, i} + αX _i + U _i

Onde

eu denota o indivíduo em particular

Y = Salário por hora (em $)

X = anos de educação

D ₂ = 1 se feminino, 0 caso contrário

D ₃ = 1 se casado, 0 caso contrário

Esta especificação não permite que possa haver uma interação que ocorra entre as duas variáveis ​​qualitativas, D ₂ e D ₃ . Por exemplo, uma mulher casada pode receber salários diferentes dos de um homem solteiro por um valor que não é o mesmo que a soma das diferenças por ser apenas mulher e apenas ser casada. Então, o efeito dos dummies interagindo na média de Y não é simplesmente aditivo como no caso da especificação acima, mas também multiplicativo , e a determinação dos salários pode ser especificada como:

Y _i = β ₁ + β ₂ D _{2, i} + β ₃ D _{3, i} + β ₄ (D _{2, i} D _{3, i} ) + αX _i + U _i

Aqui,

β ₂ = efeito diferencial de ser mulher

β ₃ = efeito diferencial de ser casado

β ₄ = efeito adicional diferencial de ser tanto do sexo feminino e casada

Por esta equação, na ausência de um erro diferente de zero, o salário de um homem solteiro é β ₁ + αX _i , o de uma mulher solteira é β ₁ + β ₂ + αX _i , o de ser um homem casado é β ₁ + β ₃ + αX _i , e o de ser uma mulher casada é β ₁ + β ₂ + β ₃ + β ₄ + αX _i (onde qualquer uma das estimativas dos coeficientes das dummies pode ser positivo, zero, ou negativo).

Assim, uma dummy de interação (produto de duas dummies) pode alterar a variável dependente do valor que ela obtém quando as duas dummies são consideradas individualmente.

No entanto, o uso de produtos de variáveis ​​dummy para capturar interações pode ser evitado usando um esquema diferente para categorizar os dados - um que especifica categorias em termos de combinações de características. Se deixarmos

D ₄ = 1 se solteira, 0 caso contrário

D ₅ = 1 se homem casado, 0 caso contrário

D ₆ = 1 se mulher casada, 0 caso contrário

então é suficiente especificar a regressão

Y _i = δ ₁ + δ ₄ D _{4, i} + δ ₅ D _{5, i} + δ ₆ D _{6, i} + αX _i + U _i .

Então, com o termo choque zero, o valor da variável dependente é δ ₁ + αX _i para os homens solteiros da categoria base, δ ₁ + δ ₄ + αX _i para mulheres solteiras, δ ₁ + δ ₅ + αX _i para homens casados ​​e δ ₁ + δ ₆ + αX _i para mulheres casadas. Esta especificação envolve o mesmo número de variáveis ​​do lado direito que a especificação anterior com um termo de interação, e os resultados da regressão para o valor previsto da variável dependente contingente em X _i , para qualquer combinação de características qualitativas, são idênticos entre esta especificação e a especificação de interação.

Variáveis ​​dependentes fictícias

O que acontece se a variável dependente for uma dummy?

Um modelo com uma variável dependente dummy (também conhecido como variável dependente qualitativa) é aquele em que a variável dependente, conforme influenciada pelas variáveis ​​explicativas, é de natureza qualitativa. Algumas decisões sobre 'quanto' de um ato deve ser realizado envolvem uma tomada de decisão prévia sobre se o ato deve ser executado ou não. Por exemplo, a quantidade de produto a produzir, o custo a ser incorrido, etc. envolvem decisões anteriores sobre se produzir ou não, se gastar ou não, etc. Essas "decisões anteriores" tornam-se dummies dependentes no modelo de regressão.

Por exemplo, a decisão de um trabalhador de fazer parte da força de trabalho torna-se uma variável dependente dummy. A decisão é dicotômica , ou seja, a decisão tem dois desfechos possíveis: sim e não. Assim, a variável dependente dummy Participação assumiria o valor 1 se participasse, 0 se não participasse. Alguns outros exemplos de manequins dependentes dicotômicos são citados abaixo:

Decisão: Escolha da Profissão. Dependent Dummy: Supervisory = 1 se supervisor, 0 se não for supervisor.

Decisão: Filiação a um Partido Político. Dependent Dummy: Affiliation = 1 se afiliado ao partido, 0 se não for afiliado.

Decisão: Aposentadoria. Dependente Fictício: Aposentado = 1 se aposentado, 0 se não aposentado.

Quando a variável dummy dependente qualitativa tem mais de dois valores (como afiliação a muitos partidos políticos), ela se torna um modelo multirresposta ou multinomial ou policotômico .

Modelos de variáveis ​​fictícias dependentes

A análise de modelos de variáveis ​​dummy dependentes pode ser feita por meio de diferentes métodos. Um desses métodos é o método OLS usual , que neste contexto é denominado modelo de probabilidade linear . Um método alternativo é assumir que existe uma variável latente contínua não observável Y ^* e que a variável dicotômica observada Y = 1 se Y ^* > 0, 0 caso contrário. Este é o conceito subjacente dos modelos logit e probit . Esses modelos são discutidos resumidamente a seguir.

Modelo de probabilidade linear

Um modelo de mínimos quadrados ordinários em que a variável dependente Y é uma dummy dicotômica, assumindo os valores de 0 e 1, é o modelo de probabilidade linear (LPM). Suponha que consideremos a seguinte regressão:

${\ displaystyle Y_ {i} = \ alpha _ {1} + \ alpha _ {2} X_ {i} + u_ {i}}$

Onde

${\ displaystyle X}$ = renda familiar

${\ displaystyle Y = 1}$ se a casa for propriedade da família, 0 se a casa não for propriedade da família

O modelo é chamado de modelo de probabilidade linear porque a regressão é linear. A média condicional de Y _i dado X _i , escrita como , é interpretada como a probabilidade condicional de que o evento ocorrerá para aquele valor de X _i - isto é, Pr ( Y _i = 1 | X _i ). Neste exemplo, dá a probabilidade de uma casa pertencer a uma família cuja renda é dada por X _i . ${\ displaystyle \ mathbb {E} (Y_ {i} | X_ {i})}$${\ displaystyle \ mathbb {E} (Y_ {i} | X_ {i})}$

Agora, usando a suposição de OLS , obtemos ${\ displaystyle E (u_ {i} | X_ {i}) = 0}$

${\ displaystyle \ mathbb {E} (Y_ {i} | X_ {i}) = \ alpha _ {1} + \ alpha _ {2} X_ {i}}$

Alguns problemas são inerentes ao modelo LPM:

1. A linha de regressão não será bem ajustada e, portanto, as medidas de significância, como R ² , não serão confiáveis.
2. Os modelos que são analisados ​​usando a abordagem LPM terão distúrbios heterocedásticos .
3. O termo de erro terá uma distribuição não normal.
4. O LPM pode fornecer valores previstos da variável dependente maiores que 1 ou menores que 0. Isso será difícil de interpretar, pois os valores previstos são probabilidades, que devem estar entre 0 e 1.
5. Pode haver uma relação não linear entre as variáveis ​​do modelo LPM, caso em que a regressão linear não ajustará os dados com precisão.

Alternativas ao LPM

Figura 4: Uma função de distribuição cumulativa.

Para evitar as limitações do LPM, é necessário um modelo que tenha a característica de que à medida que a variável explicativa, X _i , aumenta, P _i = E ( Y _i = 1 | X _i ) deve permanecer no intervalo entre 0 e 1. Assim, a relação entre as variáveis ​​independentes e dependentes é necessariamente não linear.

Para este propósito, uma função de distribuição cumulativa (CDF) pode ser usada para estimar a regressão da variável dependente dummy. A Figura 4 mostra uma curva em forma de 'S', que se assemelha ao CDF de uma variável aleatória. Neste modelo, a probabilidade está entre 0 e 1 e a não linearidade foi capturada. A escolha do CDF a ser usado agora é a questão.

Podem ser usados ​​dois CDFs alternativos: os CDFs logísticos e normais . O CDF logístico dá origem ao modelo logit e o CDF normal dá origem ao modelo probit .

Modelo Logit

As deficiências do LPM levaram ao desenvolvimento de um modelo mais refinado e aprimorado, denominado modelo logit. No modelo logit, a distribuição cumulativa do termo de erro na equação de regressão é logística. A regressão é mais realista por ser não linear.

O modelo logit é estimado usando a abordagem de máxima verossimilhança . Neste modelo, que é a probabilidade da variável dependente assumir o valor de 1 dada a variável independente é: ${\ displaystyle P (Y = 1 | X)}$

${\ displaystyle P_ {i} = {\ frac {1} {1 + e ^ {- z_ {i}}}} \ = {\ frac {e ^ {z_ {i}}} {1 + e ^ {z_ {eu}}}}\ }$

onde . ${\ displaystyle z_ {i} = \ alpha _ {1} + \ alpha _ {2} X_ {i} + u_ {i}}$

O modelo é então expresso na forma de odds ratio : o que é modelado na regressão logística é o logaritmo natural das probabilidades, sendo as probabilidades definidas como . Tomando o logaritmo natural das probabilidades, o logit ( L _i ) é expresso como ${\ displaystyle P / (1-P)}$

${\ displaystyle L_ {i} = \ ln \ left ({\ frac {P_ {i}} {1-P_ {i}}} \ right) = z_ {i} = \ alpha _ {1} + \ alpha _ {2} X_ {i}.}$

Esta relação mostra que L _i é linear em relação a X _i , mas as probabilidades não são lineares em termos de X _i .

Modelo probit

Outro modelo desenvolvido para compensar as desvantagens do LPM é o modelo probit. O modelo probit usa a mesma abordagem para não linearidade que o modelo logit; entretanto, ele usa o CDF normal em vez do CDF logístico.

Veja também

• Regressão binária
• Teste de comida
• Testando hipóteses
• Função de indicador
• Função discriminante linear
• Multicolinearidade

Referências

Leitura adicional

• Asteriou, Dimitrios; Hall, SG (2015). "Variáveis ​​fictícias". Econometria aplicada (3ª ed.). Londres: Palgrave Macmillan. pp. 209–230. ISBN   978-1-137-41546-2 .
• Kooyman, Marius A. (1976). Variáveis ​​fictícias em econometria . Tilburg: Tilburg University Press. ISBN   90-237-2919-6 .

links externos

• Maathuis, Marloes (2007). "Capítulo 7: Regressão de variável fictícia" (PDF) . Stat 423: Regressão aplicada e análise de variância . Arquivado do original (PDF) em 16 de dezembro de 2011.
• Fox, John (2010). "Regressão variável simulada" (PDF) .
• Baker, Samuel L. (2006). "Variáveis ​​fictícias" (PDF) . Arquivado do original (PDF) em 1º de março de 2006.