Grupo fundamental - Fundamental group

No campo matemático da topologia algébrica , o grupo fundamental de um espaço topológico é o grupo das classes de equivalência sob homotopia dos loops contidos no espaço. Ele registra informações sobre a forma básica, ou orifícios, do espaço topológico . O grupo fundamental é o primeiro e mais simples grupo de homotopia . O grupo fundamental é uma homotopia invariantes espaços -topological que são equivalentes homotopy (ou o caso mais forte de homeomorphic ) têm isomorphic grupos fundamentais.

Intuição

Comece com um espaço (por exemplo, uma superfície) e algum ponto nele, e todos os loops começando e terminando neste ponto - caminhos que começam neste ponto, vagueiam e eventualmente retornam ao ponto inicial. Dois loops podem ser combinados de maneira óbvia: viaje ao longo do primeiro loop e depois ao longo do segundo. Dois loops são considerados equivalentes se um puder ser deformado no outro sem quebrar. O conjunto de todos esses loops com este método de combinação e esta equivalência entre eles é o grupo fundamental para aquele espaço particular.

História

Henri Poincaré definiu o grupo fundamental em 1895 em seu artigo " Analysis situs ". O conceito surgiu na teoria das superfícies de Riemann , na obra de Bernhard Riemann , Poincaré e Felix Klein . Ele descreve as propriedades de monodromia de funções de valor complexo , bem como fornece uma classificação topológica completa de superfícies fechadas .

Definição

Ao longo deste artigo, X é um espaço topológico. Um exemplo típico é uma superfície como a mostrada à direita. Além disso, é um ponto em X denominado ponto-base . (Como é explicado abaixo, seu papel é bastante auxiliar.) A ideia da definição do grupo de homotopia é medir quantas curvas (em termos gerais) em X podem ser deformadas umas nas outras. A definição precisa depende da noção de homotopia de loops, que é explicada primeiro. ${\ displaystyle x_ {0}}$

Homotopia de loops

Dado um espaço topológico X , um loop baseado em${\ displaystyle x_ {0}}$ é definido como uma função contínua (também conhecido como mapa contínuo )

${\ displaystyle \ gamma \ dois pontos [0,1] \ a X}$

de forma que o ponto inicial e o ponto final são ambos iguais a . ${\ displaystyle \ gamma (0)}$${\ displaystyle \ gamma (1)}$${\ displaystyle x_ {0}}$

Uma homotopia é uma interpolação contínua entre dois loops. Mais precisamente, uma homotopia entre dois loops (com base no mesmo ponto ) é um mapa contínuo ${\ displaystyle \ gamma, \ gamma '\ dois pontos [0,1] \ a X}$${\ displaystyle x_ {0}}$

${\ displaystyle h \ dois pontos [0,1] \ vezes [0,1] \ a X,}$

de tal modo que

• ${\ displaystyle h (0, t) = x_ {0}}$apesar de tudo , o ponto de partida da homotopia é para todo t (que muitas vezes é considerado um parâmetro de tempo).${\ displaystyle t \ in [0,1],}$${\ displaystyle x_ {0}}$
• ${\ displaystyle h (1, t) = x_ {0}}$para tudo o que existe, da mesma forma o ponto final permanece para todo t .${\ displaystyle t \ in [0,1],}$${\ displaystyle x_ {0}}$
• ${\ displaystyle h (r, 0) = \ gamma (r), h (r, 1) = \ gamma '(r)}$para todos .${\ displaystyle r \ in [0,1]}$

Se um tal homotopy h existe, e são referidos como sendo homotópicas . A relação " é homotópica com " é uma relação de equivalência para que o conjunto de classes de equivalência possa ser considerado: ${\ displaystyle \ gamma}$${\ displaystyle \ gamma '}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma '}$

${\ displaystyle \ pi _ {1} (X, x_ {0}): = \ {{\ text {todos os loops}} \ gamma {\ text {baseado em}} x_ {0} \} / {\ text { homotopia}}}$.

Este conjunto (com a estrutura de grupo descrita abaixo) é chamado de grupo fundamental do espaço topológico X no ponto de base . O objetivo de considerar as classes de equivalência de loops até a homotopia, em oposição ao conjunto de todos os loops (o chamado espaço de loop de X ) é que este último, embora seja útil para vários fins, é um objeto bastante grande e pesado . Em contraste, o quociente acima é, em muitos casos, mais gerenciável e computável. ${\ displaystyle x_ {0}}$

Estrutura de grupo

Pela definição acima, é apenas um conjunto. Ele se torna um grupo (e, portanto, merece o nome de grupo fundamental ) usando a concatenação de loops. Mais precisamente, dados dois loops , seu produto é definido como o loop ${\ displaystyle \ pi _ {1} (X, x_ {0})}$${\ displaystyle \ gamma _ {0}, \ gamma _ {1}}$

${\ displaystyle {\ begin {alinhados} \ gamma _ {0} \ cdot \ gamma _ {1} \ dois pontos [0,1] & \ para X \\ (\ gamma _ {0} \ cdot \ gamma _ {1 }) (t) & = {\ begin {cases} \ gamma _ {0} (2t) & 0 \ leq t \ leq {\ tfrac {1} {2}} \\\ gamma _ {1} (2t-1 ) & {\ tfrac {1} {2}} \ leq t \ leq 1. \ end {casos}} \ end {alinhado}}}$

Assim, o loop primeiro segue o loop com "duas vezes a velocidade" e depois com "duas vezes a velocidade". ${\ displaystyle \ gamma _ {0} \ cdot \ gamma _ {1}}$${\ displaystyle \ gamma _ {0}}$${\ displaystyle \ gamma _ {1}}$

O produto de duas classes de homotopia de loops e é então definido como . Pode-se comprovar que este produto não depende da escolha de representantes e, portanto, proporciona um funcionamento bem definido no conjunto . Esta operação se transforma em um grupo. Seu elemento neutro é o loop constante, que permanece em todos os tempos t . O inverso de um (classe de homotopia de um) loop é o mesmo loop, mas percorrido na direção oposta. Mais formalmente, ${\ displaystyle [\ gamma _ {0}]}$${\ displaystyle [\ gamma _ {1}]}$${\ displaystyle [\ gamma _ {0} \ cdot \ gamma _ {1}]}$${\ displaystyle \ pi _ {1} (X, x_ {0})}$${\ displaystyle \ pi _ {1} (X, x_ {0})}$${\ displaystyle x_ {0}}$

${\ displaystyle \ gamma ^ {- 1} (t): = \ gamma (1-t)}$.

Dados três loops baseados no produto ${\ displaystyle \ gamma _ {0}, \ gamma _ {1}, \ gamma _ {2},}$

${\ displaystyle (\ gamma _ {0} \ cdot \ gamma _ {1}) \ cdot \ gamma _ {2}}$

é a concatenação desses loops, percorrendo e depois com velocidade quádrupla e, em seguida, com velocidade dupla. Por comparação, ${\ displaystyle \ gamma _ {0}}$${\ displaystyle \ gamma _ {1}}$${\ displaystyle \ gamma _ {2}}$

${\ displaystyle \ gamma _ {0} \ cdot (\ gamma _ {1} \ cdot \ gamma _ {2})}$

atravessa os mesmos caminhos (na mesma ordem), mas com velocidade dupla e com velocidade quádrupla. Assim, por causa das velocidades diferentes, os dois caminhos não são idênticos. O axioma da associatividade${\ displaystyle \ gamma _ {0}}$${\ displaystyle \ gamma _ {1}, \ gamma _ {2}}$

${\ displaystyle [\ gamma _ {0}] \ cdot \ left ([\ gamma _ {1}] \ cdot [\ gamma _ {2}] \ right) = \ left ([\ gamma _ {0}] \ cdot [\ gamma _ {1}] \ right) \ cdot [\ gamma _ {2}]}$

portanto, depende crucialmente do fato de que os caminhos são considerados até a homotopia. De fato, os dois compostos acima são homotópicos, por exemplo, ao loop que atravessa todos os três loops com velocidade tripla. O conjunto de loops baseados até a homotopia, equipado com a operação acima, portanto, se transforma em um grupo. ${\ displaystyle \ gamma _ {0}, \ gamma _ {1}, \ gamma _ {2}}$${\ displaystyle \ pi _ {1} (X, x_ {0})}$

Dependência do ponto de base

Embora o grupo fundamental em geral dependa da escolha do ponto de base, verifica-se que, até o isomorfismo (na verdade, mesmo até o isomorfismo interno ), essa escolha não faz diferença, desde que o espaço X seja conectado por caminho . Para espaços conectados por caminhos, portanto, muitos autores escrevem em vez de . ${\ displaystyle \ pi _ {1} (X)}$${\ displaystyle \ pi _ {1} (X, x_ {0})}$

Exemplos concretos

Esta seção lista alguns exemplos básicos de grupos fundamentais. Para começar, no espaço euclidiano ( ) ou em qualquer subconjunto convexo de, há apenas uma classe de homotopia de loops, e o grupo fundamental é, portanto, o grupo trivial com um elemento. De maneira mais geral, qualquer domínio de estrela e, ainda mais geralmente, qualquer espaço contrátil tem um grupo fundamental trivial. Assim, o grupo fundamental não faz distinção entre tais espaços. ${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n},}$

A 2-esfera

Um espaço conectado por caminho cujo grupo fundamental é trivial é chamado simplesmente conectado . Por exemplo, a esfera 2 representada à direita e também todas as esferas de dimensões superiores estão simplesmente conectadas. A figura ilustra uma homotopia contraindo um loop particular para o loop constante. Essa ideia pode ser adaptada a todos os loops de forma que haja um ponto que não está na imagem de No entanto, como existem loops tais que (construídos a partir da curva de Peano , por exemplo), uma prova completa requer uma análise mais cuidadosa com ferramentas de topologia algébrica, como o teorema de Seifert-van Kampen ou o teorema de aproximação celular . ${\ displaystyle S ^ {2} = \ left \ {(x, y, z) \ in \ mathbb {R} ^ {3} \ mid x ^ {2} + y ^ {2} + z ^ {2} = 1 \ direita \}}$${\ displaystyle \ gamma}$${\ displaystyle (x, y, z) \ in S ^ {2}}$${\ displaystyle \ gamma.}$${\ displaystyle \ gamma ([0,1]) = S ^ {2}}$

O circulo

O círculo (também conhecido como 1 esfera)

${\ displaystyle S ^ {1} = \ left \ {(x, y) \ in \ mathbb {R} ^ {2} \ mid x ^ {2} + y ^ {2} = 1 \ right \}}$

não está simplesmente conectado. Em vez disso, cada classe de homotopia consiste em todos os loops que enrolam ao redor do círculo um determinado número de vezes (que pode ser positivo ou negativo, dependendo da direção do enrolamento). O produto de um loop que gira em torno de m vezes e outro que gira em torno de n vezes é um loop que gira em torno de vezes. Portanto, o grupo fundamental do círculo é isomórfico ao grupo aditivo de inteiros . Este fato pode ser usado para fornecer provas do teorema do ponto fixo de Brouwer e do teorema de Borsuk-Ulam na dimensão 2. ${\ displaystyle m + n}$${\ displaystyle (\ mathbb {Z}, +),}$

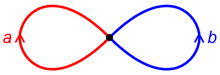
O número oito

O grupo fundamental da figura oito é o grupo livre em duas letras. A ideia de provar isso é a seguinte: escolhendo o ponto base para ser o ponto onde os dois círculos se encontram (pontilhados em preto na imagem à direita), qualquer loop pode ser decomposto como ${\ displaystyle \ gamma}$

${\ displaystyle \ gamma = a ^ {n_ {1}} b ^ {m_ {1}} \ cdots a ^ {n_ {k}} b ^ {m_ {k}}}$

onde a e b são os dois loops enrolando em torno de cada metade da figura, conforme ilustrado, e os expoentes são inteiros. Ao contrário do grupo fundamental da figura oito não é abeliano : as duas formas de compor a e b não são homotópicas entre si: ${\ displaystyle n_ {1}, \ dots, n_ {k}, m_ {1}, \ dots, m_ {k}}$${\ displaystyle \ pi _ {1} \ left (S ^ {1} \ right),}$

${\ displaystyle [a] \ cdot [b] \ neq [b] \ cdot [a].}$

De maneira mais geral, o grupo fundamental de um buquê de r círculos é o grupo livre em r letras.

O grupo fundamental de uma soma de cunha de dois espaços conectados de caminho X e Y pode ser calculado como o produto livre dos grupos fundamentais individuais:

${\ displaystyle \ pi _ {1} (X \ vee Y) \ cong \ pi _ {1} (X) * \ pi _ {1} (Y).}$

Isso generaliza as observações acima, uma vez que a figura oito é a soma de dois círculos.

O grupo fundamental do avião perfurado em n pontos é também o grupo livre com n geradores. O i- ésimo gerador é a classe do loop que contorna o i- ésimo punção sem contornar nenhum outro punção.

Gráficos

O grupo fundamental também pode ser definido para estruturas discretas. Em particular, consideram um gráfico conectado G = ( V , E ) , com um vértice designado v ₀ em V . Os loops em G são os ciclos que começam e terminam em v ₀ . Deixe- T ser uma árvore geradora de G . Cada laço simples em G contém exatamente uma aresta em E \ T ; cada loop em G é uma concatenação desses loops simples. Portanto, o grupo fundamental de um gráfico é um grupo livre , em que o número de geradores é exactamente o número de arestas em E \ T . Este número é igual a | E | - | V | + 1 .

Por exemplo, suponha que G tenha 16 vértices dispostos em 4 filas de 4 vértices cada, com arestas conectando vértices adjacentes horizontal ou verticalmente. Então G tem 24 arestas no total, e o número de arestas em cada árvore geradora é 16 - 1 = 15 , então o grupo fundamental de G é o grupo livre com 9 geradores. Observe que G possui 9 "orifícios", semelhante a um buquê de 9 círculos, que possui o mesmo grupo fundamental.

Grupos de nós

Os grupos de nós são, por definição, o grupo fundamental do complemento de um nó K embutido.Por exemplo, o grupo de nós do nó do trevo é conhecido como o grupo de trança que dá outro exemplo de um grupo fundamental não abeliano. A apresentação de Wirtinger descreve explicitamente os grupos de nós em termos de geradores e relações com base em um diagrama do nó. Portanto, grupos de nós têm algum uso na teoria de nós para distinguir entre nós: senão for isomórfico a algum outro grupode nós de outro nó K ' , então K não pode ser transformado em.Assim, o nó de trevo não pode ser continuamente transformado em círculo ( também conhecido como unknot ), já que este último possui grupo de nós. Existem, no entanto, nós que não podem ser deformados uns nos outros, mas têm grupos de nós isomórficos. ${\ displaystyle \ mathbb {R} ^ {3}.}$ ${\ displaystyle B_ {3},}$${\ displaystyle \ pi _ {1} \ left (\ mathbb {R} ^ {3} \ setminus K \ right)}$${\ displaystyle \ pi _ {1} \ left (\ mathbb {R} ^ {3} \ setminus K '\ right)}$${\ displaystyle K '.}$${\ displaystyle \ mathbb {Z}}$

Superfícies orientadas

O grupo fundamental de uma superfície orientável gênero n pode ser calculado em termos de geradores e relações como

${\ displaystyle \ left \ langle A_ {1}, B_ {1}, \ ldots, A_ {n}, B_ {n} \ left | A_ {1} B_ {1} A_ {1} ^ {- 1} B_ {1} ^ {- 1} \ cdots A_ {n} B_ {n} A_ {n} ^ {- 1} B_ {n} ^ {- 1} \ right. \ Right \ rangle.}$

Inclui o toro , sendo o caso do gênero 1, cujo grupo fundamental é

${\ displaystyle \ left \ langle A_ {1}, B_ {1} \ left | A_ {1} B_ {1} A_ {1} ^ {- 1} B_ {1} ^ {- 1} \ right. \ right \ rangle \ cong \ mathbb {Z} ^ {2}.}$

Grupos topológicos

O grupo fundamental de um grupo topológico X (com respeito ao ponto base sendo o elemento neutro) é sempre comutativo. Em particular, o grupo fundamental de um grupo de Lie é comutativo. Na verdade, a estrutura de grupo em X dota de outra estrutura de grupo: dados dois loops e em X , outro loop pode ser definido usando a multiplicação de grupo em X : ${\ displaystyle \ pi _ {1} (X)}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma '}$${\ displaystyle \ gamma \ star \ gamma '}$

${\ displaystyle \ left (\ gamma \ star \ gamma '\ right) (x) = \ gamma (x) \ cdot \ gamma' (x).}$

Esta operação binária no conjunto de todos os loops é a priori independente da descrita acima. No entanto, o argumento Eckmann-Hilton mostra que ele de fato concorda com a concatenação de loops acima e, além disso, a estrutura de grupo resultante é abeliana. ${\ displaystyle \ star}$

Uma inspeção da prova mostra que, mais geralmente, é abeliano para qualquer H-espaço X , ou seja, a multiplicação não precisa ter um inverso, nem precisa ser associativa. Por exemplo, isto mostra que o grupo fundamental de um espaço circuito de um outro espaço topológico Y , é abeliano. Ideias relacionadas levam ao cálculo de Heinz Hopf da cohomologia de um grupo de Lie . ${\ displaystyle \ pi _ {1} (X)}$ ${\ displaystyle X = \ Omega (Y),}$

Funcionalidade

Se é um mapa contínuo, e com então todo laço em X com ponto base pode ser composto com f para produzir um laço em Y com ponto base Esta operação é compatível com a relação de equivalência de homotopia e com composição de laços. O homomorfismo de grupo resultante , denominado homomorfismo induzido , é escrito como ou, mais comumente, ${\ displaystyle f \ dois pontos X \ a Y}$${\ displaystyle x_ {0} \ in X}$${\ displaystyle y_ {0} \ in Y}$${\ displaystyle f (x_ {0}) = y_ {0},}$${\ displaystyle x_ {0}}$${\ displaystyle y_ {0}.}$${\ displaystyle \ pi (f)}$

${\ displaystyle f _ {*} \ dois pontos \ pi _ {1} (X, x_ {0}) \ a \ pi _ {1} (Y, y_ {0}).}$

Este mapeamento de mapas contínuos para homomorfismos de grupo é compatível com a composição de mapas e morfismos de identidade. No jargão da teoria das categorias , a formação de associar a um espaço topológico seu grupo fundamental é, portanto, um functor

${\ displaystyle {\ begin {alinhados} \ pi _ {1} \ colon \ mathbf {Top} _ {*} & \ to \ mathbf {Grp} \\ (X, x_ {0}) & \ mapsto \ pi _ {1} (X, x_ {0}) \ end {alinhado}}}$

da categoria de espaços topológicos juntamente com um ponto de base para a categoria de grupos . Acontece que este functor não distingue mapas que são homotópicos em relação ao ponto base: se f , g  : X → Y são mapas contínuos com f ( x ₀ ) = g ( x ₀ ) = y ₀ , e f e g são homotópicos em relação a { x ₀ }, então f _∗ = g _∗ . Como consequência, dois espaços conectados por caminho equivalentes de homotopia têm grupos fundamentais isomórficos:

${\ displaystyle X \ simeq Y \ Rightarrow \ pi _ {1} (X, x_ {0}) \ cong \ pi _ {1} (Y, y_ {0}).}$

Por exemplo, a inclusão do círculo no plano perfurado

${\ displaystyle S ^ {1} \ subset \ mathbb {R} ^ {2} \ setminus \ {0 \}}$

é uma equivalência de homotopia e, portanto, produz um isomorfismo de seus grupos fundamentais.

O funtor de grupo fundamental leva produtos a produtos e coprodutos a coprodutos. Ou seja, se X e Y estão conectados por caminho, então

${\ displaystyle \ pi _ {1} (X \ times Y, (x_ {0}, y_ {0})) \ cong \ pi _ {1} (X, x_ {0}) \ times \ pi _ {1 } (Y, y_ {0}).}$

Resultados abstratos

Como foi mencionado acima, calcular o grupo fundamental de espaços topológicos relativamente simples tende a não ser totalmente trivial, mas requer alguns métodos de topologia algébrica.

Relação com o primeiro grupo de homologia

A abelianização do grupo fundamental pode ser identificada com o primeiro grupo de homologia do espaço.

Um caso especial do teorema de Hurewicz afirma que o primeiro grupo de homologia singular é, coloquialmente falando, a mais próxima aproximação do grupo fundamental por meio de um grupo abeliano. Em mais detalhes, o mapeamento da classe de homotopia de cada loop para a classe de homologia do loop fornece um homomorfismo de grupo${\ displaystyle H_ {1} (X)}$

${\ displaystyle \ pi _ {1} (X) \ a H_ {1} (X)}$

do grupo fundamental de um espaço topológico X ao seu primeiro grupo de homologia singular Este homomorfismo não é em geral um isomorfismo, uma vez que o grupo fundamental pode ser não abeliano, mas o grupo de homologia é, por definição, sempre abeliano. Esta diferença é, no entanto, a única: se X está conectado por caminho, esse homomorfismo é sobrejetivo e seu núcleo é o subgrupo comutador do grupo fundamental, de forma que é isomórfico à abelianização do grupo fundamental. ${\ displaystyle H_ {1} (X).}$${\ displaystyle H_ {1} (X)}$

Colagem de espaços topológicos

Generalizando a declaração acima, para uma família de espaços de caminho ligados o grupo fundamental é o produto livre dos grupos fundamentais do Este fato é um caso especial do teorema Seifert-van Kampen , o que permite calcular, de forma mais geral, os grupos fundamentais de espaços que são colados de outros espaços. Por exemplo, a 2-esfera pode ser obtida colando duas cópias de meias-esferas ligeiramente sobrepostas ao longo de uma vizinhança do equador . Nesse caso, o rendimento do teorema é trivial, uma vez que as duas meias-esferas são contráteis e, portanto, têm grupo fundamental trivial. Os grupos fundamentais de superfícies, como mencionado acima, também podem ser calculados usando este teorema. ${\ displaystyle X_ {i},}$${\ textstyle \ pi _ {1} \ left (\ bigvee _ {i \ in I} X_ {i} \ right)}$${\ displaystyle X_ {i}.}$${\ displaystyle S ^ {2}}$${\ displaystyle \ pi _ {1} \ left (S ^ {2} \ right)}$

No jargão da teoria das categorias, o teorema pode ser afirmado de forma concisa, dizendo que o functor de grupo fundamental leva pushouts (na categoria de espaços topológicos) ao longo de inclusões em pushouts (na categoria de grupos).

Coberturas

Dado um espaço topológico B , um mapa contínuo

${\ displaystyle f: E \ to B}$

é chamado de cobertura ou E é chamado de espaço de cobertura de B se cada ponto b em B admite uma vizinhança aberta U tal que existe um homeomorfismo entre a pré - imagem de U e uma união disjunta de cópias de U (indexada por algum conjunto I ) ,

${\ displaystyle \ varphi: \ bigsqcup _ {i \ in I} U \ para f ^ {- 1} (U)}$

de tal forma que é o mapa de projeção padrão${\ displaystyle \ pi \ circ \ varphi}$${\ displaystyle \ bigsqcup _ {i \ in I} U \ to U.}$

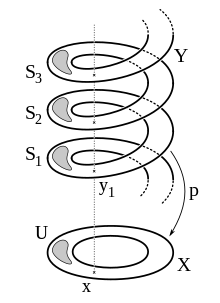
Cobertura universal

Uma cobertura é chamada de cobertura universal se E estiver, além da condição anterior, simplesmente conectada. É universal no sentido de que todos os outros revestimentos podem ser construídos por identificar adequadamente pontos em E . Conhecendo uma cobertura universal

${\ displaystyle p: {\ widetilde {X}} \ a X}$

de um espaço topológico X é útil na compreensão de seu grupo fundamental de várias maneiras: primeiro, identifica-se com o grupo de transformações de convés , ou seja, o grupo de homeomorfismos que comutam com o mapa para X , ou seja, Outra relação com o grupo fundamental é que podem ser identificados com a fibra. Por exemplo, o mapa ${\ displaystyle \ pi _ {1} (X)}$ ${\ displaystyle \ varphi: {\ widetilde {X}} \ to {\ widetilde {X}}}$${\ displaystyle p \ circ \ varphi = p.}$${\ displaystyle \ pi _ {1} (X, x)}$${\ displaystyle p ^ {- 1} (x).}$

${\ displaystyle p: \ mathbb {R} \ to S ^ {1}, t \ mapsto \ exp (2 \ pi it)}$

(ou, equivalentemente, ) é uma cobertura universal. As transformações de baralho são os mapas para Isso está de acordo com a identificação em particular, isso prova a afirmação acima${\ displaystyle \ pi: \ mathbb {R} \ to \ mathbb {R} / \ mathbb {Z}, \ t \ mapsto [t]}$${\ displaystyle t \ mapsto t + n}$${\ displaystyle n \ in \ mathbb {Z}.}$${\ displaystyle p ^ {- 1} (1) = \ mathbb {Z},}$${\ displaystyle \ pi _ {1} \ left (S ^ {1} \ right) \ cong \ mathbb {Z}.}$

Qualquer caminho conectado, localmente conectado por caminho e localmente simplesmente conectado ao espaço topológico X admite uma cobertura universal. Uma construção abstrata procede analogamente ao grupo fundamental tomando pares ( x , γ), onde x é um ponto em X e γ é uma classe de homotopia de caminhos de x ₀ a x . A passagem de um espaço topológico a sua cobertura universal pode ser usado para a compreensão da geometria da X . Por exemplo, o teorema de uniformização mostra que qualquer superfície de Riemann simplesmente conectada é (isomórfica a) um ou o meio plano superior . As superfícies gerais de Riemann surgem então como quocientes de ações de grupo nessas três superfícies. ${\ displaystyle S ^ {2},}$ ${\ displaystyle \ mathbb {C},}$

O quociente de uma ação de um grupo ( discreto ) G em um espaço Y simplesmente conectado tem um grupo fundamental

${\ displaystyle \ pi _ {1} (Y / G) \ cong G.}$

A título de exemplo, o espaço projetivo real n- dimensional real é obtido como o quociente da esfera n- dimensional pela ação antípoda do grupo enviando para As é simplesmente conectado por n ≥ 2, é uma cobertura universal nestes casos , o que implica para n ≥ 2. ${\ displaystyle \ mathbb {R} \ mathrm {P} ^ {n}}$${\ displaystyle S ^ {n}}$${\ displaystyle \ mathbb {Z} / 2}$${\ displaystyle x \ in S ^ {n}}$${\ displaystyle -x.}$${\ displaystyle S ^ {n}}$${\ displaystyle \ mathbb {R} \ mathrm {P} ^ {n}}$${\ displaystyle \ pi _ {1} \ left (\ mathbb {R} \ mathrm {P} ^ {n} \ right) \ cong \ mathbb {Z} / 2}$

Grupos de mentiras

Deixe L ser um ligado, simplesmente ligado grupo de Lie compacto , por exemplo, o grupo unitário especial SU ( n ), e deixe Γ ser um subgrupo finito de L . Então o espaço homogêneo X  =  G / Γ tem Γ grupo fundamental, que atua pela multiplicação direito sobre o espaço cobertura universal G . Entre as muitas variantes desta construção, uma das mais importantes é dada pelos espaços localmente simétricos X  = Γ \ G / K , onde

• G é um grupo de Lie não compacto conectado de forma simples (muitas vezes semissimples ),
• K é um subgrupo compacto máximo de G
• Γ é um subgrupo de G livre de torção contável e discreto .

Neste caso, o grupo fundamental é Γ e o espaço de cobertura universal G / K é realmente contraível (pela decomposição de Cartan para grupos de Lie ).

Como exemplo, tome G  = SL (2, R ), K  = SO (2) e Γ qualquer subgruente de congruência livre de torção do grupo modular SL (2, Z ).

Da compreensão explícita, também segue que o espaço de cobertura universal de um grupo topológico H conectado por caminho é novamente um grupo topológico G conectado por caminho . Além disso, o mapa de cobertura é um homomorfismo aberto contínuo de G em H com kernel Γ, um subgrupo normal discreto fechado de G :

${\ displaystyle 1 \ a \ Gamma \ a G \ a H \ a 1.}$

Uma vez que L é um grupo ligado com uma acção contínua por conjugação sobre uma Γ grupo discreto, deve agir trivialmente, de modo que Γ tem de ser um subgrupo do centro de L . Em particular, π ₁ ( H ) = Γ é um grupo abeliano ; isso também pode ser facilmente visto diretamente sem o uso de espaços de cobertura. O grupo G é chamado o grupo cobertura universal de  H .

Como sugere o grupo de cobertura universal, há uma analogia entre o grupo fundamental de um grupo topológico e o centro de um grupo; isso é elaborado na Malha de grupos de cobertura .

Fibrações

Fibrações fornecem um meio muito poderoso para calcular grupos de homotopia. Um fibraç~ao f o chamado espaço total , e o espaço de base B tem, em particular, a propriedade de que todas as suas fibrassão homotopy equivalente e, por conseguinte, não podem ser distinguidos utilizando grupos fundamentais (e os grupos de homotopia superior), desde que B é caminho -conectado. Portanto, o espaço E pode ser considerado um "produto torcido " da base do espaço B e da fibra. A grande importância das fibrações para o cálculo de grupos de homotopia decorre de uma longa sequência exata${\ displaystyle f ^ {- 1} (b)}$ ${\ displaystyle F = f ^ {- 1} (b).}$

${\ displaystyle \ dots \ to \ pi _ {2} (B) \ to \ pi _ {1} (F) \ to \ pi _ {1} (E) \ to \ pi _ {1} (B) \ para \ pi _ {0} (F) \ para \ pi _ {0} (E)}$

desde que B esteja conectado ao caminho. O termo é o segundo grupo de homotopia de B , que é definido como o conjunto de classes de homotopia de mapas de a B , em analogia direta com a definição de${\ displaystyle \ pi _ {2} (B)}$${\ displaystyle S ^ {2}}$${\ displaystyle \ pi _ {1}.}$

Se E acontecer de ser conectado por caminho e simplesmente conectado, esta sequência se reduz a um isomorfismo

${\ displaystyle \ pi _ {1} (B) \ cong \ pi _ {0} (F)}$

o que generaliza o fato acima sobre a cobertura universal (o que equivale ao caso em que a fibra F também é discreta). Se, em vez disso, F estiver conectado e simplesmente conectado, ele se reduz a um isomorfismo

${\ displaystyle \ pi _ {1} (E) \ cong \ pi _ {1} (B).}$

Além disso, a sequência pode ser continuada à esquerda com os grupos de homotopia mais elevados dos três espaços, o que dá algum acesso à computação de tais grupos na mesma linha. ${\ displaystyle \ pi _ {n}}$

Grupos de Lie clássica

Tais sequências de fibra pode ser usado para calcular indutivamente grupos fundamentais de grupos de Lie clássicos compactos, como o grupo unitária especial com Este grupo actua transitively na esfera unitária dentro O estabilizador de um ponto na esfera é isomorfa a Em seguida, pode ser mostrado que este produz uma sequência de fibra ${\ displaystyle \ mathrm {SU} (n),}$${\ displaystyle n \ geq 2.}$${\ displaystyle S ^ {2n-1}}$${\ displaystyle \ mathbb {C} ^ {n} = \ mathbb {R} ^ {2n}.}$${\ displaystyle \ mathrm {SU} (n-1).}$

${\ displaystyle \ mathrm {SU} (n-1) \ para \ mathrm {SU} (n) \ para S ^ {2n-1}.}$

Uma vez que a esfera tem dimensão de pelo menos 3, o que implica ${\ displaystyle n \ geq 2,}$${\ displaystyle S ^ {2n-1}}$

${\ displaystyle \ pi _ {1} \ left (S ^ {2n-1} \ right) \ cong \ pi _ {2} \ left (S ^ {2n-1} \ right) = 1.}$

A longa sequência exata mostra então um isomorfismo

${\ displaystyle \ pi _ {1} (\ mathrm {SU} (n)) \ cong \ pi _ {1} (\ mathrm {SU} (n-1)).}$

Já que é um único ponto, então isso é trivial, isso mostra que está simplesmente conectado para todos${\ displaystyle \ mathrm {SU} (1)}$${\ displaystyle \ pi _ {1} (\ mathrm {SU} (1))}$${\ displaystyle \ mathrm {SU} (n)}$${\ displaystyle n.}$

O grupo fundamental de grupos de Lie não compactos pode ser reduzido ao caso compacto, uma vez que tal grupo é homotópico ao seu subgrupo compacto máximo. Esses métodos fornecem os seguintes resultados:

Grupo de Lie clássico compacto G	Grupo de Lie não compacto	${\ displaystyle \ pi _ {1}}$
grupo unitário especial ${\ displaystyle \ mathrm {SU} (n)}$	${\ displaystyle \ mathrm {SL} (n, \ mathbb {C})}$	1
grupo unitário ${\ displaystyle \ mathrm {U} (n)}$	${\ displaystyle \ mathrm {GL} (n, \ mathbb {C}), \ mathrm {Sp} (n, \ mathbb {R})}$	${\ displaystyle \ mathbb {Z}}$
grupo ortogonal especial ${\ displaystyle \ mathrm {SO} (n)}$	${\ displaystyle \ mathrm {SO} (n, \ mathbb {C})}$	${\ displaystyle \ mathbb {Z} / 2}$para e para${\ displaystyle n \ geq 3}$${\ displaystyle \ mathbb {Z}}$${\ displaystyle n = 2}$
grupo simplético compacto ${\ displaystyle \ mathrm {Sp} (n)}$	${\ displaystyle \ mathrm {Sp} (n, \ mathbb {C})}$	1

Um segundo método de cálculo de grupos fundamentais se aplica a todos os grupos de Lie compactos conectados e usa a maquinaria do toro máximo e o sistema de raiz associado . Especificamente, deixa ser um toro mima num grupo de Lie compacto ligado e deixar ser o álgebra de Lie de O mapa exponencial${\ displaystyle T}$${\ displaystyle K,}$${\ displaystyle {\ mathfrak {t}}}$${\ displaystyle T.}$

${\ displaystyle \ exp: {\ mathfrak {t}} \ to T}$

é uma fibração e, portanto, seu kernel se identifica com o mapa ${\ displaystyle \ Gamma \ subset {\ mathfrak {t}}}$${\ displaystyle \ pi _ {1} (T).}$

${\ displaystyle \ pi _ {1} (T) \ to \ pi _ {1} (K)}$

pode ser mostrado como sobrejetivo com kernel dado pelo conjunto I de combinação linear inteira de coroots . Isso leva ao cálculo

${\ displaystyle \ pi _ {1} (K) \ cong \ Gamma / I.}$

Este método mostra, por exemplo, que qualquer grupo compacto de Lie conectado para o qual o sistema raiz associado é do tipo${\ displaystyle G_ {2}}$ é simplesmente conectado. Assim, existe (até o isomorfismo) apenas um grupo de Lie compacto conectado tendo álgebra de Lie do tipo ; este grupo está simplesmente conectado e tem um centro trivial. ${\ displaystyle G_ {2}}$

Grupo de caminho de borda de um complexo simplicial

Quando o espaço topológico é homeomorfo a um complexo simplicial , seu grupo fundamental pode ser descrito explicitamente em termos de geradores e relações .

Se X é um ligado complexo simplicial , uma borda caminho em X é definido como sendo uma cadeia de vértices ligadas por arestas em X . Dois caminhos de borda são referidos como sendo de borda equivalente se um pode ser obtido a partir da outra, alternando sucessivamente, entre uma ponta e as duas bordas opostas de um triângulo em X . Se v é um vértice fixo em X , um loop de aresta em v é um caminho de aresta começando e terminando em v . O grupo de caminho de borda E ( X ,  v ) é definido como o conjunto de classes de equivalência de borda de loops de borda em v , com produto e inverso definidos por concatenação e reversão de loops de borda.

O grupo do caminho da borda é naturalmente isomórfico a π ₁ (| X |,  v ), o grupo fundamental da realização geométrica | X | de X . Uma vez que depende apenas do 2-esqueleto X ² de X (ou seja, os vértices, arestas e triângulos de X ), os grupos π ₁ (| X |, v ) e π ₁ (| X ² |,  v ) são isomórficos.

O grupo do caminho de borda pode ser descrito explicitamente em termos de geradores e relações . Se T é uma árvore geradora máxima no esqueleto 1 de X , então E ( X ,  v ) é canonicamente isomórfico ao grupo com geradores (os caminhos de borda orientados de X não ocorrem em T ) e relações (as equivalências de borda correspondendo a triângulos em X ). Um resultado semelhante se prende T é substituído por qualquer simplesmente ligado -em particular, contraível -subcomplex de X . Isso geralmente fornece uma maneira prática de computar grupos fundamentais e pode ser usado para mostrar que todo grupo finitamente apresentado surge como o grupo fundamental de um complexo simplicial finito. É também um dos métodos clássicos usados ​​para superfícies topológicas , que são classificadas por seus grupos fundamentais.

O espaço de cobertura universal de um complexo simplicial conectado finito X também pode ser descrito diretamente como um complexo simplicial usando caminhos de borda. Seus vértices são pares ( w , γ) onde w é um vértice de X e γ é uma classe de equivalência de arestas de caminhos de v a w . Os k -simplices contendo ( w , γ) correspondem naturalmente aos k -simplices contendo w . Cada novo vértice u do k -simplexo fornece uma aresta wu e, portanto, por concatenação, um novo caminho γ _u de v para u . Os pontos ( w , γ) e ( u , γ _u ) são os vértices do simplex "transportado" no espaço de cobertura universal. O grupo de borda caminho actua naturalmente por concatenação, preservando a estrutura simplicial, e o espaço quociente é apenas X .

É bem sabido que este método também pode ser usado para calcular o grupo fundamental de um espaço topológico arbitrário. Isso, sem dúvida, era conhecido por Eduard Čech e Jean Leray e apareceu explicitamente como uma observação em um artigo de André Weil ; vários outros autores como Lorenzo Calabi, Wu Wen-tsün e Nodar Berikashvili também publicaram provas. No caso mais simples de um espaço compacto X com uma cobertura aberta finita em que todas as interseções finitas não vazias de conjuntos abertos na cobertura são contráteis, o grupo fundamental pode ser identificado com o grupo de caminho de borda do complexo simplicial correspondente ao nervo da cobertura .

Realizabilidade

• Cada grupo pode ser realizado como o grupo fundamental de um complexo CW conectado de dimensão 2 (ou superior). Porém, conforme observado acima, apenas grupos livres podem ocorrer como grupos fundamentais de complexos CW unidimensionais (ou seja, gráficos).
• Cada grupo finitamente apresentado pode ser realizado como o grupo fundamental de uma variedade compacta , conectada e lisa de dimensão 4 (ou superior). Mas existem severas restrições sobre quais grupos ocorrem como grupos fundamentais de variedades de baixa dimensão. Por exemplo, nenhum grupo abeliano livre de classificação 4 ou superior pode ser realizado como o grupo fundamental de uma variedade de dimensão 3 ou inferior. Pode-se provar que todo grupo pode ser realizado como o grupo fundamental de um espaço de Hausdorff compacto se e somente se não houver cardeal mensurável .

Conceitos relacionados

Grupos de homotopia mais elevados

Grosso modo, o grupo fundamental detecta a estrutura de orifícios unidimensionais de um espaço, mas não orifícios em dimensões superiores, como para a esfera 2. Tais "buracos de dimensões superiores" podem ser detectadas utilizando as maiores grupos de homotopia , que são definidos como consistindo de classes de homotopia de (basepoint-preservando) mapeia a partir de X . Por exemplo, o teorema de Hurewicz implica que o n -ésimo grupo de homotopia da n -sfera é (para todos ) ${\ displaystyle \ pi _ {n} (X)}$${\ displaystyle S ^ {n}}$${\ displaystyle n \ geq 1}$

${\ displaystyle \ pi _ {n} (S ^ {n}) = \ mathbb {Z}.}$

Como foi mencionado no cálculo acima de grupos de Lie clássicos, grupos de homotopia mais altos podem ser relevantes até mesmo para o cálculo de grupos fundamentais. ${\ displaystyle \ pi _ {1}}$

Espaço de loop

O conjunto de loops baseados (como está, isto é, não levado à homotopia) em um espaço pontudo X , dotado da topologia aberta compacta , é conhecido como o espaço de loop , denotado O grupo fundamental de X está em bijeção com o conjunto de componentes do caminho de seu espaço de loop: ${\ displaystyle \ Omega X.}$

${\ displaystyle \ pi _ {1} (X) \ cong \ pi _ {0} (\ Omega X).}$

Grupóide fundamental

O grupóide fundamental é uma variante do grupo fundamental que é útil em situações onde a escolha de um ponto base é indesejável. É definido considerando primeiro a categoria de caminhos , ou seja, funções contínuas ${\ displaystyle x_ {0} \ in X}$${\ displaystyle X,}$

${\ displaystyle \ gamma \ dois pontos [0, r] \ a X}$,

onde r é um número real não negativo arbitrário. Como o comprimento r é variável nesta abordagem, tais caminhos podem ser concatenados como estão (ou seja, não até a homotopia) e, portanto, geram uma categoria. Dois desses caminhos com os mesmos pontos finais e comprimento r , resp. r ' são considerados equivalentes se existem números reais tais que e são homotópicos em relação aos seus pontos finais, onde${\ displaystyle \ gamma, \ gamma '}$${\ displaystyle u, v \ geqslant 0}$${\ displaystyle r + u = r '+ v}$${\ displaystyle \ gamma _ {u}, \ gamma '_ {v} \ dois pontos [0, r + u] \ to X}$${\ displaystyle \ gamma _ {u} (t) = {\ begin {cases} \ gamma (t), & t \ in [0, r] \\\ gamma (r), & t \ in [r, r + u ]. \ end {cases}}}$

A categoria de caminhos até essa relação de equivalência é denotada. Cada morfismo em é um isomorfismo , com o inverso dado pelo mesmo caminho percorrido na direção oposta. Essa categoria é chamada de grupóide . Ele reproduz o grupo fundamental desde ${\ displaystyle \ Pi (X).}$${\ displaystyle \ Pi (X)}$

${\ displaystyle \ pi _ {1} (X, x_ {0}) = \ mathrm {Hom} _ {\ Pi (X)} (x_ {0}, x_ {0})}$.

De forma mais geral, pode-se considerar o grupóide fundamental em um conjunto A de pontos de base, escolhidos de acordo com a geometria da situação; por exemplo, no caso do círculo, que pode ser representado como a união de dois conjuntos abertos conectados cuja interseção tem dois componentes, pode-se escolher um ponto base em cada componente. O teorema de van Kampen admite uma versão para grupóides fundamentais que fornece, por exemplo, outra maneira de calcular o grupo fundamental (oid) de${\ displaystyle S ^ {1}.}$

Sistemas locais

De um modo geral, as representações podem servir para exibir características de um grupo por meio de suas ações em outros objetos matemáticos, geralmente espaços vetoriais . As representações do grupo fundamental têm um significado muito geométrico: qualquer sistema local (ou seja, um feixe em X com a propriedade de que localmente em uma vizinhança U suficientemente pequena de qualquer ponto em X , a restrição de F é um feixe constante da forma ) dá origem à chamada representação de monodromia , uma representação do grupo fundamental em um espaço vetorial n- dimensional . Por outro lado, qualquer representação em um espaço conectado por caminho X surge dessa maneira. Esta equivalência de categorias entre representações de e sistemas locais é usada, por exemplo, no estudo de equações diferenciais , como as equações de Knizhnik-Zamolodchikov . ${\ displaystyle {\ mathcal {F}}}$${\ displaystyle {\ mathcal {F}} | _ {U} = \ mathbb {Q} ^ {n}}$${\ displaystyle \ mathbb {Q}}$${\ displaystyle \ pi _ {1} (X)}$

Étale fundamental grupo

Em geometria algébrica , o denominado grupo fundamental étale é usado como substituto do grupo fundamental. Desde a topologia de Zariski em uma algébrica variedade ou esquema X é muito mais grosseiro do que, digamos, a topologia de subconjuntos abertos em que não é mais significativa a considerar aplicações contínuas de um intervalo de X . Em vez disso, a abordagem desenvolvida por Grothendieck consiste em construir , considerando todos os finitos tampas étalé de X . Eles servem como um análogo algebro-geométrico de coberturas com fibras finitas. ${\ displaystyle \ mathbb {R} ^ {n},}$${\ displaystyle \ pi _ {1} ^ {\ text {et}}}$

Isso produz uma teoria aplicável em situações em que nenhuma intuição topológica clássica de grande generalidade está disponível, por exemplo, para variedades definidas sobre um campo finito . Além disso, o grupo fundamental étale de um campo é seu grupo de Galois (absoluto) . Por outro lado, para as variedades suaves X sobre os números complexos, o grupo fundamental étale retém muitas das informações inerentes ao grupo fundamental clássico: o primeiro é a complementação profinita do último.

Grupo fundamental de grupos algébricos

O grupo fundamental de um sistema raiz é definido, em analogia ao cálculo para grupos de Lie. Isso permite definir e usar o grupo fundamental de um grupo algébrico linear semi-simples G , que é uma ferramenta básica útil na classificação de grupos algébricos lineares.

Grupo fundamental de conjuntos simpliciais

A relação de homotopia entre 1-simplicos de um conjunto simplicial X é uma relação de equivalência se X for um complexo de Kan, mas não necessariamente em geral. Assim, de um complexo de Kan pode ser definido como o conjunto de classes de homotopia de 1-simplicos. O grupo fundamental de um conjunto arbitrário simplicial X são definidos para ter o grupo de homotopy sua realização topológico , isto é, o espaço topológico obtido por colagem simplices topológicos como prescrito pela estrutura conjunto simplicial de X . ${\ displaystyle \ pi _ {1}}$${\ displaystyle | X |,}$

Veja também

• Grupo fundamental Orbifold

Notas

Referências

• Adams, John Frank (1978), Infinite loop spaces , Annals of Mathematics Studies, 90 , Princeton University Press , ISBN 978-0-691-08207-3, MR  0505692
• Brown, Ronald (2006), Topology and Groupoids , Booksurge, ISBN 1-4196-2722-8
• Bump, Daniel (2013), Lie Groups , Graduate Texts in Mathematics, 225 (2ª ed.), Springer, doi : 10.1007 / 978-1-4614-8024-2 , ISBN 978-1-4614-8023-5
• Crowell, Richard H .; Fox, Ralph (1963), Introdução à Teoria dos Nó , Springer
• El Zein, Fouad; Suciu, Alexander I .; Tosun, Meral; Uludağ, Muhammed; Yuzvinsky, Sergey (2010), Arrangements, Local Systems and Singularities: CIMPA Summer School, Galatasaray University, Istanbul, 2007 , ISBN 978-3-0346-0208-2
• Forster, Otto (1981), Lectures on Riemann Surfaces , ISBN 0-387-90617-7
• Fulton, William (1995), Algebraic Topology: A First Course , Springer, ISBN 9780387943275
• Goerss, Paul G .; Jardine, John F. (1999), Simplicial Homotopy Theory , Progress in Mathematics, 174 , Basel, Boston, Berlin: Birkhäuser, ISBN 978-3-7643-6064-1
• Grothendieck, Alexandre ; Raynaud, Michèle (2003) [1971], Séminaire de Géométrie Algébrique du Bois Marie - 1960-61 - Revêtements étales et groupe fondamental - (SGA 1) (Documentos Mathématiques 3 ) , Paris: Société Mathématique de France , pp. Xviii + 327 , veja Exp. V, IX, X., arXiv : math.AG/0206203 , ISBN 978-2-85629-141-2
• Hall, Brian C. (2015), Lie Groups, Lie Algebras, and Representations: An Elementary Introduction , Graduate Texts in Mathematics, 222 (2ª ed.), Springer, ISBN 978-3319134666
• Hatcher, Allen (2002), Algebraic Topology , Cambridge University Press, ISBN 0-521-79540-0
• Peter Hilton e Shaun Wylie , Homology Theory , Cambridge University Press (1967) [advertência: esses autores usam contra- homologia para cohomologia ]
• Humphreys, James E. (2004), Linear Algebraic Groups , Graduate Texts in Mathematics, Springer, ISBN 9780387901084
• Humphreys, James E. (1972), Introdução a Lie Algebras and Representation Theory , ISBN 0-387-90052-7
• Maunder, CRF (janeiro de 1996), Algebraic Topology , Dover Publications , ISBN 0-486-69131-4
• Massey, William S. (1991), A Basic Course in Algebraic Topology , Springer, ISBN 038797430X
• Maio, J. Peter (1999), A Concise Course in Algebraic Topology , ISBN 9780226511832
• Deane Montgomery e Leo Zippin, Topological Transformation Groups , Interscience Publishers (1955)
• Munkres, James R. (2000), Topologia , Prentice Hall , ISBN 0-13-181629-2
• Rotman, Joseph (1998-07-22), An Introduction to Algebraic Topology , Springer-Verlag , ISBN 0-387-96678-1
• Rubei, Elena (2014), Algebraic Geometry, a concise dictionary , Berlin / Boston: Walter De Gruyter, ISBN 978-3-11-031622-3
• Seifert, Herbert ; Threlfall, William (1980), A Textbook of Topology , traduzido por Heil, Wolfgang, Academic Press , ISBN 0-12-634850-2
• Singer, Isadore. M .; Thorpe, JA (1976-12-10), Lecture Notes on Elementary Topology and Geometry , ISBN 0-387-90202-3
• Spanier, Edwin H. (1989), Algebraic Topology , Springer, ISBN 0-387-94426-5
• Strom, Jeffrey (2011), Modern Classical Homotopy Theory , AMS, ISBN 9780821852866

links externos

• Weisstein, Eric W. "Grupo fundamental" . MathWorld .
• Dylan GL Allegretti, Conjuntos Simpliciais e Teorema de Van Kampen : Uma discussão sobre o grupóide fundamental de um espaço topológico e o grupóide fundamental de um conjunto simplicial
• Animações para apresentar o grupo fundamental de Nicolas Delanoue
• Conjuntos de pontos de base e grupóides fundamentais: discussão sobre o fluxo de matemática
• Groupoids em Matemática