Poset graduado - Graded poset

Um conjunto de potência , parcialmente ordenado por inclusão , com classificação definida como número de elementos, forma um poset graduado.

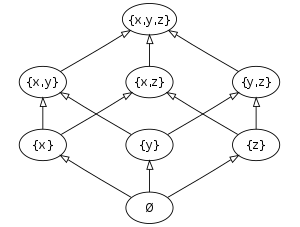
Em matemática , no ramo da combinatória , um poset graduado é um conjunto parcialmente ordenado (poset) P equipado com uma função de classificação ρ de P ao conjunto N de todos os números naturais . ρ deve satisfazer as duas propriedades a seguir:

• A função de classificação é compatível com a ordenação, o que significa que para cada x e y na ordem com x  <  y , deve ser o caso que ρ ( x ) <  ρ ( y ), e
• A classificação é consistente com a relação cobrindo da encomenda, o que significa que para cada x e y para o qual y tampas X , que deve ser o caso que ρ ( y ) =  ρ ( x ) + 1.

O valor da função de classificação para um elemento do poset é chamado de classificação . Às vezes, um poset classificado é chamado de poset classificado, mas essa frase tem outros significados; consulte Poset classificado . Uma classificação ou nível de classificação de um poset graduado é o subconjunto de todos os elementos do poset que possuem um determinado valor de classificação.

Posets graduados desempenham um papel importante na combinatória e podem ser visualizados por meio de um diagrama de Hasse .

Exemplos

Alguns exemplos de posets graduados (com a função de classificação entre parênteses) são:

• os números naturais N , com sua ordem usual (posto: o próprio número), ou algum intervalo [0,  N ] deste poset,
• N ⁿ , com a ordem do produto (soma dos componentes), ou um subposet dela que é um produto de intervalos,
• os inteiros positivos, ordenados por divisibilidade (número de fatores primos, contados com multiplicidade), ou um subposet dele formado pelos divisores de um N fixo ,
• a rede booleana de subconjuntos finitos de um conjunto (número de elementos do subconjunto),
• a rede de partições de um conjunto em partes finitas, ordenadas por refinamento reverso (número de partes),
• a rede de partições de um conjunto finito X , ordenado por refinamento (número de elementos de X menos número de partes),
• um grupo e um conjunto gerador, ou equivalentemente seu gráfico de Cayley , ordenados pela ordem de Bruhat forte ou fraca e classificados por comprimento de palavra (comprimento da palavra reduzida mais curta).
  • Em particular para grupos Coxeter , por exemplo, permutações de um conjunto de n- elementos totalmente ordenado , com a ordem Bruhat fraca ou forte (número de inversões adjacentes),
• redes geométricas , como a rede de subespaços de um espaço vetorial (dimensão do subespaço),
• a rede distributiva de conjuntos inferiores finitos de outro poset (número de elementos),
• Rede de Young , uma instância particular do exemplo anterior (número de caixas no diagrama de Young),
• redes de rosto de politopos convexos (dimensão da face, mais um),
• politopos abstratos ("distância" da menor face, menos uma),
• complexos simpliciais abstratos (número de elementos do simplex).

Caracterizações alternativas

A rede N ₅ não pode ser graduada.

Um poset limitado admite uma classificação se e somente se todas as cadeias máximas em P tiverem o mesmo comprimento: definir a classificação do menor elemento como 0 determina a função de classificação completamente. Isso cobre muitos casos finitos de interesse; veja a imagem para um exemplo negativo. No entanto, posets ilimitados podem ser mais complicados.

Uma função de classificação candidata, compatível com a ordenação, transforma um poset em poset graduado se e somente se, sempre que se tiver x  <  z com z de classificação n +1, um elemento y de classificação n pode ser encontrado com x  ≤  y  <  z . Esta condição é suficiente porque se z é considerado uma cobertura de x , a única escolha possível é y  =  x mostrando que as classificações de x e z diferem por 1, e é necessário porque em um poset graduado pode-se tomar para y qualquer elemento de classificação máxima com x  ≤  y  <  z , que sempre existe e é coberto por z .

Freqüentemente, um poset vem com um candidato natural para uma função de posto; por exemplo, se seus elementos são subconjuntos finitos de algum conjunto base B , pode-se tomar o número de elementos desses subconjuntos. Então, o critério que acabamos de fornecer pode ser mais prático do que a definição, porque evita a menção de capas. Por exemplo, se B é ele mesmo um poset, e P consiste em seus conjuntos inferiores finitos (subconjuntos para os quais, com cada um de seus elementos, todos os elementos menores também estão no subconjunto), então o critério é automaticamente satisfeito, uma vez que para conjuntos inferiores x  ⊆  z sempre há um elemento máximo de z que está ausente de x , e pode ser removido de z para formar y .

Em alguns posets comuns, como a estrutura de face de um politopo convexo, há uma graduação natural por dimensão , que se usada como função de classificação forneceria o elemento mínimo, a face vazia, classificação -1. Nesses casos, pode ser conveniente dobrar a definição declarada acima juntando o valor –1 ao conjunto de valores permitidos para a função de classificação. Permitir números inteiros arbitrários como classificação, entretanto, daria uma noção fundamentalmente diferente; por exemplo, a existência de um elemento mínimo não seria mais garantida.

Um poset graduado (com classificações inteiras positivas) não pode ter nenhum elemento x para o qual cadeias arbitrariamente longas com o maior elemento x existam, caso contrário, ele teria que ter elementos de classificação arbitrariamente pequena (e eventualmente negativa). Por exemplo, os inteiros (com a ordem usual) não podem ser um poset graduado, nem pode qualquer intervalo (com mais de um elemento) de números racionais ou reais . (Em particular, posets graduados são bem fundamentados , o que significa que eles satisfazem a condição de cadeia descendente (DCC): eles não contêm nenhuma cadeia descendente infinita .) Doravante, consideraremos, portanto, apenas posets em que isso não acontece. Isto implica que sempre que x  <  y podemos começar a partir de x para y escolhendo repetidamente uma tampa, um número finito de vezes. Também significa que (para funções de classificação de número inteiro positivo) a compatibilidade de ρ com a ordenação segue do requisito sobre coberturas. Como uma variante da definição de um poset graduado, Birkhoff permite que funções de classificação tenham valores inteiros arbitrários (em vez de apenas não negativos). Nesta variante, os inteiros podem ser graduados (pela função de identidade) em sua configuração, e a compatibilidade das classificações com a ordenação não é redundante. Como uma terceira variante, Brightwell e West definem uma função de classificação como com valor inteiro, mas não exigem sua compatibilidade com a ordem; portanto, essa variante pode classificar até, por exemplo, os números reais por qualquer função, já que o requisito sobre coberturas é vazio para este exemplo.

Observe que posets graduados não precisam satisfazer a condição de cadeia ascendente (ACC): por exemplo, os números naturais contêm a cadeia ascendente infinita . ${\ displaystyle 0 <1 <2 <\ cdots}$

Um poset é classificado se e somente se cada componente conectado de seu gráfico de comparabilidade for classificado, portanto, caracterizações adicionais irão supor que esse gráfico de comparabilidade seja conectado. Em cada componente conectado, a função de classificação é exclusiva apenas até uma mudança uniforme (portanto, a função de classificação pode sempre ser escolhida de forma que os elementos de classificação mínima em seu componente conectado tenham classificação 0).

Se P tem o menor elemento Ô, então ser graduado é equivalente à condição de que para qualquer elemento x todas as cadeias máximas no intervalo [Ô,  x ] tenham o mesmo comprimento. Esta condição é necessária uma vez que cada passo em uma cadeia máxima é uma relação de cobertura, que deve mudar a classificação em 1. A condição também é suficiente, pois quando ela se mantém, pode-se usar o comprimento mencionado para definir a classificação de x (o comprimento de uma cadeia finita é seu número de "etapas", portanto, um a menos que seu número de elementos), e sempre que x cobre y , juntando x a uma cadeia máxima em [Ô, y ] dá uma cadeia máxima em [Ô, x ] .

Se P também tem um maior elemento Î (de modo que é um poset limitado ), então a condição anterior pode ser simplificada para o requisito de que todas as cadeias máximas em P tenham o mesmo comprimento (finito). Isto é suficiente, uma vez que qualquer par de correntes máximas em [O, X ] pode ser estendido por uma corrente máxima na [ x , i] para dar um par de correntes máximas em P .

Nota Stanley define um poset a ser graduado de comprimento n se todas as suas cadeias máximas tiverem comprimento n (Stanley 1997, p.99). Esta definição é dada em um contexto onde o interesse é principalmente em posets finitos, e embora o livro subsequentemente muitas vezes elimine a parte "de comprimento n ", não parece apropriado usar isso como definição de "graduado" para posets gerais, porque ( 1) não diz nada sobre posets cujas cadeias máximas são infinitas, em particular (2) exclui posets importantes como a rede de Young . Também não está claro por que em um poset graduado todos os elementos mínimos, bem como todos os elementos máximos, devem ter o mesmo comprimento, mesmo que Stanley dê exemplos deixando claro que ele pretende exigir isso (ibid, pp.216 e 219).

O caso usual

Muitos autores em combinatória definem posets graduados de tal forma que todos os elementos mínimos de P devem ter classificação 0 e, além disso, existe uma classificação máxima r que é a classificação de qualquer elemento máximo. Então, ser graduado significa que todas as cadeias máximas têm comprimento r , como indicado acima. Nesse caso, diz-se que P tem posto r .

Além disso, neste caso, aos níveis de classificação estão associados os números de classificação ou números de Whitney . Esses números são definidos por = número de elementos de P com classificação i . ${\ displaystyle W_ {0}, W_ {1}, W_ {2}, ...}$${\ displaystyle W_ {i}}$

Os números de Whitney estão ligados a muitos teoremas combinatórios importantes . O exemplo clássico é o teorema de Sperner , que pode ser formulado da seguinte forma:

Para o conjunto de poderes de cada conjunto finito, a cardinalidade máxima de uma família Sperner é igual ao número máximo de Whitney . ${\ displaystyle {\ mathcal {P}} (S)}$ ${\ displaystyle S}$

Isso significa:

Cada conjunto de poderes finito tem a propriedade Sperner

Veja também

• Graduado (matemática)
• Prewellordering - um prewellordering com uma norma é análogo a um poset graduado, substituindo um mapa para os inteiros por um mapa para os ordinais
• Produto Star , um método para combinar dois posets graduados

Notas

Referências

• Stanley, Richard (1997). Enumerative Combinatorics (vol.1, Cambridge Studies in Advanced Mathematics 49) . Cambridge University Press . ISBN   0-521-66351-2 .
• Anderson, Ian (1987). Combinatória de conjuntos finitos . Oxford, Reino Unido: Clarendon Press . ISBN   0-19-853367-5 .
• Engel, Konrad (1997). Teoria de Sperner . Cambridge, UK (et al.): Cambridge University Press. ISBN   0-521-45206-6 .
• Kung, Joseph PS; Rota, Gian-Cario ; Yan, Catherine H. (2009). Combinatorics: The Rota Way . Cambridge, UK (et al.): Cambridge University Press. ISBN   978-0-521-73794-4 .