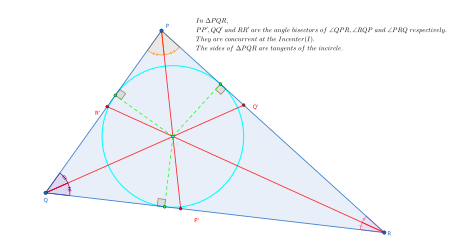
No centro - Incenter

O ponto de intersecção das bissetoras dos ângulos dos 3 ângulos do triângulo ABC é o incenter (denotado por I). O incircle (cujo centro é I) toca cada lado do triângulo.

Na geometria , o incentivo de um triângulo é o centro do triângulo , um ponto definido para qualquer triângulo de uma forma que é independente da posição ou escala do triângulo. O incentivo pode ser definido de forma equivalente como o ponto onde as bissetoras do ângulo interno do triângulo se cruzam, como o ponto equidistante dos lados do triângulo, como o ponto de junção do eixo medial e o ponto mais interno da transformação do triângulo, e como o ponto central do círculo inscrito do triângulo.

Junto com o centróide , o circuncentro e o ortocentro , é um dos quatro centros triangulares conhecidos pelos gregos antigos e o único que geralmente não se encontra na linha de Euler . É o centro primeiro da lista, X (1), em Clark Kimberling 's Encyclopedia of Centros Triângulo , e o elemento de identidade do grupo multiplicativo de centros triângulo.

Para polígonos com mais de três lados, o incentivo só existe para polígonos tangenciais - aqueles que têm um incircle que é tangente a cada lado do polígono. Nesse caso, o incentivo é o centro desse círculo e está igualmente distante de todos os lados.

Definição e construção

É um teorema da geometria euclidiana que as três bissetoras dos ângulos internos de um triângulo se encontram em um único ponto. Em Euclides 's Elementos , proposição 4 do livro IV mostra que este ponto é também o centro do círculo inscrito do triângulo. O próprio incircle pode ser construído deixando-se cair uma perpendicular do incentivo a um dos lados do triângulo e desenhando um círculo com esse segmento como seu raio.

O incentivo encontra-se a distâncias iguais dos três segmentos de linha que formam os lados do triângulo, e também das três linhas que contêm esses segmentos. É o único ponto igualmente distante dos segmentos de reta, mas há mais três pontos igualmente distantes das retas, os excentros, que formam os centros dos círculos de um dado triângulo. O incentivo e os excentros juntos formam um sistema ortocêntrico .

O eixo medial de um polígono é o conjunto de pontos cujo vizinho mais próximo no polígono não é único: esses pontos são equidistantes de dois ou mais lados do polígono. Um método para calcular eixos mediais é usar a transformada de fogo de grama , na qual se forma uma sequência contínua de curvas de deslocamento , cada uma a alguma distância fixa do polígono; o eixo medial é traçado pelos vértices dessas curvas. No caso de um triângulo, o eixo medial consiste em três segmentos das bissetoras do ângulo, conectando os vértices do triângulo ao incentivo, que é o ponto único na curva de deslocamento mais interna. O esqueleto reto , definido de maneira semelhante a partir de um tipo diferente de curva de deslocamento, coincide com o eixo medial para polígonos convexos e, portanto, também tem sua junção no incentivo.

Provas

Prova de proporção

Que a bissecção de e se encontre em , e a bissecção de e se encontre em , e se encontre em . ${\ displaystyle \ angle {BAC}}$${\ displaystyle {\ overline {BC}}}$${\ displaystyle D}$${\ displaystyle \ angle {ABC}}$${\ displaystyle {\ overline {AC}}}$${\ displaystyle E}$${\ displaystyle {\ overline {AD}}}$${\ displaystyle {\ overline {BE}}}$${\ displaystyle {I}}$

E deixe e se encontram em . ${\ displaystyle {\ overline {CI}}}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle {F}}$

Então temos que provar que é a bissecção de . ${\ displaystyle {\ overline {CI}}}$${\ displaystyle \ angle {ACB}}$

No , . ${\ displaystyle \ triangle {ACF}}$${\ displaystyle {\ overline {AC}}: {\ overline {AF}} = {\ overline {CI}}: {\ overline {IF}}}$

No , . ${\ displaystyle \ triangle {BCF}}$${\ displaystyle {\ overline {BC}}: {\ overline {BF}} = {\ overline {CI}}: {\ overline {IF}}}$

Portanto, para que . ${\ displaystyle {\ overline {AC}}: {\ overline {AF}} = {\ overline {BC}}: {\ overline {BF}}}$${\ displaystyle {\ overline {AC}}: {\ overline {BC}} = {\ overline {AF}}: {\ overline {BF}}}$

Assim é a bissecção de${\ displaystyle {\ overline {CF}}}$${\ displaystyle \ angle {ACB}}$

Prova perpendicular

Uma linha que é uma bissetriz do ângulo é equidistante de suas duas linhas ao medir pela perpendicular. No ponto onde duas bissetoras se cruzam, este ponto é perpendicularmente equidistante das linhas de formação do ângulo final (porque elas estão à mesma distância dessa borda oposta do ângulo) e, portanto, encontra-se em sua linha bissetriz do ângulo.

Relação com os lados e vértices do triângulo

Coordenadas trilineares

As coordenadas trilineares de um ponto no triângulo fornecem a razão das distâncias para os lados do triângulo. Coordenadas trilineares para o incentivo são dadas por

${\ displaystyle \ 1: 1: 1.}$

A coleção de centros de triângulo pode receber a estrutura de um grupo sob multiplicação coordenada de coordenadas trilineares; neste grupo, o incentivo constitui o elemento de identidade .

Coordenadas baricêntricas

As coordenadas baricêntricas para um ponto em um triângulo fornecem pesos tais que o ponto é a média ponderada das posições dos vértices do triângulo. As coordenadas baricêntricas para o incentivo são fornecidas por

${\ displaystyle \ a: b: c}$

onde , e são os comprimentos dos lados do triângulo, ou equivalentemente (utilizando a lei dos senos ) por ${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$

${\ displaystyle \ sin (A): \ sin (B): \ sin (C)}$

onde , e são os ângulos nos três vértices. ${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle C}$

Coordenadas cartesianas

As coordenadas cartesianas do incentivo são uma média ponderada das coordenadas dos três vértices usando os comprimentos laterais do triângulo em relação ao perímetro - isto é, usando as coordenadas baricêntricas fornecidas acima, normalizadas para somar à unidade - como pesos. (Os pesos são positivos para que as mentiras incentro no interior do triângulo como indicado acima). Se os três vértices estão localizados no , e , e os lados opostos desses vértices têm comprimentos correspondentes , e , em seguida, o incentro é a ${\ displaystyle (x_ {A}, y_ {A})}$${\ displaystyle (x_ {B}, y_ {B})}$${\ displaystyle (x_ {C}, y_ {C})}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle c}$

${\ displaystyle {\ bigg (} {\ frac {ax_ {A} + bx_ {B} + cx_ {C}} {a + b + c}}, {\ frac {ay_ {A} + by_ {B} + cy_ {C}} {a + b + c}} {\ bigg)} = {\ frac {a (x_ {A}, y_ {A}) + b (x_ {B}, y_ {B}) + c (x_ {C}, y_ {C})} {a + b + c}}.}$

Distâncias para vértices

Denotando o incentivo do triângulo ABC como I , as distâncias do incentivo aos vértices combinadas com os comprimentos dos lados do triângulo obedecem à equação

${\ displaystyle {\ frac {IA \ cdot IA} {CA \ cdot AB}} + {\ frac {IB \ cdot IB} {AB \ cdot BC}} + {\ frac {IC \ cdot IC} {BC \ cdot CA}} = 1.}$

Adicionalmente,

${\ displaystyle IA \ cdot IB \ cdot IC = 4Rr ^ {2},}$

onde R e R são do triângulo circumradius e inradius respectivamente.

Construções relacionadas

Outros centros

A distância do incentivo ao centróide é inferior a um terço do comprimento da mediana mais longa do triângulo.

Pelo teorema de Euler em geometria , a distância ao quadrado do incentivo I ao circuncentro O é dada por

${\ displaystyle OI ^ {2} = R (R-2r),}$

onde R e r são o circumradius e o inradius respectivamente; assim, o circumradius é pelo menos duas vezes o inradius, com igualdade apenas no caso equilátero .

A distância do incentivo ao centro N do círculo de nove pontos é

${\ displaystyle IN = {\ frac {1} {2}} (R-2r) <{\ frac {1} {2}} R.}$

A distância quadrada do incentivo ao ortocentro H é

${\ displaystyle IH ^ {2} = 2r ^ {2} -4R ^ {2} \ cos A \ cos B \ cos C.}$

As desigualdades incluem:

${\ displaystyle IG <HG, \ quad IH <HG, \ quad IG <IO, \ quad 2IN <IO.}$

O incentivo é o ponto de Nagel do triângulo medial (o triângulo cujos vértices são os pontos médios dos lados) e, portanto, fica dentro desse triângulo. Inversamente, o ponto de Nagel de qualquer triângulo é o incentivo de seu triângulo anticomplementar .

O incentivo deve estar no interior de um disco cujo diâmetro conecta o centróide G e o ortocentro H (o disco ortocentroidal ), mas não pode coincidir com o centro de nove pontos , cuja posição é fixada a 1/4 do caminho ao longo do diâmetro (mais perto de G ). Qualquer outro ponto dentro do disco ortocentroidal é o incentivo de um triângulo único.

Linha Euler

A linha de Euler de um triângulo é uma linha que passa por seu circuncentro , centróide e ortocentro , entre outros pontos. O incentivo geralmente não está na linha de Euler; está na linha de Euler apenas para triângulos isósceles , para os quais a linha de Euler coincide com o eixo de simetria do triângulo e contém todos os centros do triângulo.

Denotando a distância do incentivo à linha de Euler como d , o comprimento da mediana mais longa como v , o comprimento do lado mais longo como u , o circumradius como R , o comprimento do segmento de linha de Euler do ortocentro ao circuncentro como e , e o semiperímetro como s , as seguintes desigualdades são válidas:

${\ displaystyle {\ frac {d} {s}} <{\ frac {d} {u}} <{\ frac {d} {v}} <{\ frac {1} {3}};}$

${\ displaystyle d <{\ frac {1} {3}} e;}$

${\ displaystyle d <{\ frac {1} {2}} R.}$

Divisores de área e perímetro

Qualquer linha através de um triângulo que divide a área do triângulo e seu perímetro ao meio passa pelo incentivo do triângulo; cada linha através do incentivo que divide a área ao meio também divide o perímetro ao meio. Existem uma, duas ou três dessas linhas para qualquer triângulo.

Distâncias relativas de uma bissetriz de ângulo

Deixe X ser um ponto variável sobre a bissectriz do ângulo interno de um . Então X = I (o incentivo) maximiza ou minimiza a razão ao longo dessa bissetriz do ângulo. ${\ displaystyle {\ tfrac {BX} {CX}}}$

Referências

links externos

• Weisstein, Eric W. "Incenter" . MathWorld .