Inversão (matemática discreta) - Inversion (discrete mathematics)

Permutação com uma de suas inversões destacada

Pode ser denotada pelo par de lugares (2, 4) ou pelo par de elementos (5, 2).

Na ciência da computação e na matemática discreta , uma inversão em uma sequência é um par de elementos que estão fora de sua ordem natural .

Definições

Inversão

Deixe ser uma permutação . Se e , o par de lugares ou o par de elementos é chamado de inversão de . ${\ displaystyle \ pi}$${\ displaystyle i <j}$${\ displaystyle \ pi (i)> \ pi (j)}$${\ displaystyle (i, j)}$${\ displaystyle {\ bigl (} \ pi (i), \ pi (j) {\ bigr)}}$${\ displaystyle \ pi}$

A inversão é geralmente definida para permutações, mas também pode ser definida para sequências:
Let Ser uma sequência (ou permutação multiset ). Se e , o par de lugares ou o par de elementos é chamado de inversão de . ${\ displaystyle S}$${\ displaystyle i <j}$${\ displaystyle S (i)> S (j)}$${\ displaystyle (i, j)}$${\ displaystyle {\ bigl (} S (i), S (j) {\ bigr)}}$${\ displaystyle S}$

Para sequências, as inversões de acordo com a definição baseada em elemento não são únicas, porque diferentes pares de lugares podem ter o mesmo par de valores.

O conjunto de inversões é o conjunto de todas as inversões. O conjunto de inversão de uma permutação de acordo com a definição baseada no lugar é aquele conjunto de inversão da permutação inversa de acordo com a definição baseada no elemento, e vice-versa, apenas com os elementos dos pares trocados.

Número de inversão

O número de inversão de uma sequência é a cardinalidade do conjunto de inversão. É uma medida comum de (pré-) classificação de uma permutação ou sequência. Este valor está entre 0 e incluído. ${\ displaystyle {\ mathtt {inv}} (X)}$${\ displaystyle X = \ langle x_ {1}, \ dots, x_ {n} \ rangle}$${\ displaystyle {\ frac {n (n-1)} {2}}}$

Por exemplo, uma vez que a sequência está ordenada. Além disso, como cada par é uma inversão. Este último exemplo mostra que uma classificação ordenada intuitivamente ainda pode ter um número quadrático de inversões. ${\ displaystyle {\ mathtt {inv}} (\ langle 1,2, \ dots, n \ rangle) = 0}$${\ displaystyle {\ mathtt {inv}} (\ langle n + 1, n + 2, \ dots, 2n, 1,2, \ dots, n \ rangle) = n ^ {2}}$${\ displaystyle (1 \ leq i \ leq n <j \ leq 2n)}$

É o número de cruzamentos no diagrama de setas da permutação, sua distância tau Kendall da permutação de identidade e a soma de cada um dos vetores relacionados à inversão definidos abaixo.

Não importa se a definição de inversão baseada em lugar ou baseada em elemento é usada para definir o número de inversão, porque uma permutação e seu inverso têm o mesmo número de inversões.

Outras medidas de (pré-) classificação incluem o número mínimo de elementos que podem ser excluídos da sequência para render uma sequência totalmente classificada, o número e os comprimentos das "corridas" classificadas dentro da sequência, a regra de Spearman (soma das distâncias de cada elemento de sua posição classificada), e o menor número de trocas necessárias para classificar a sequência. Os algoritmos de classificação de comparação padrão podem ser adaptados para calcular o número de inversão no tempo O ( n log n ) .

Vetores relacionados à inversão

Três vetores semelhantes estão em uso e condensam as inversões de uma permutação em um vetor que a determina de maneira única. Eles são freqüentemente chamados de vetor de inversão ou código Lehmer . (Uma lista de fontes pode ser encontrada aqui .)

Este artigo usa o termo vetor de inversão ( ) como Volfrâmio . Os dois vetores restantes às vezes são chamados de vetor de inversão à esquerda e à direita , mas para evitar confusão com o vetor de inversão, este artigo os chama de contagem de inversão à esquerda ( ) e contagem de inversão à direita ( ). Interpretada como um número fatorial, a contagem de inversão à esquerda fornece as permutações colexicográficas reversas e a contagem de inversão à direita fornece o índice lexicográfico. ${\ displaystyle v}$${\ displaystyle l}$${\ displaystyle r}$

Diagrama de Rothe

Vetor de inversão : ${\ displaystyle v}$
Com a definição baseada em elemento é o número de inversões cujo menor componente (direito) é . ${\ displaystyle v (i)}$${\ displaystyle i}$

${\ displaystyle v (i)}$ é o número de elementos em maior do que antes . ${\ displaystyle \ pi}$${\ displaystyle i}$${\ displaystyle i}$

${\ displaystyle v (i) ~~ = ~~ \ # \ {k \ mid k> i ~ \ land ~ \ pi ^ {- 1} (k) <\ pi ^ {- 1} (i) \}}$

Contagem de inversões à esquerda : ${\ displaystyle l}$
Com a definição baseada no local é o número de inversões cujo maior componente (à direita) é . ${\ displaystyle l (i)}$${\ displaystyle i}$

${\ displaystyle l (i)}$ é o número de elementos em maior do que antes . ${\ displaystyle \ pi}$${\ displaystyle \ pi (i)}$${\ displaystyle \ pi (i)}$

${\ displaystyle l (i) ~~ = ~~ \ # \ left \ {k \ mid k <i ~ \ land ~ \ pi (k)> \ pi (i) \ right \}}$

Contagem de inversão direita , geralmente chamada de código Lehmer : ${\ displaystyle r}$
com a definição baseada em local é o número de inversões cujo menor componente (esquerdo) é . ${\ displaystyle r (i)}$${\ displaystyle i}$

${\ displaystyle r (i)}$ é o número de elementos em menor do que depois . ${\ displaystyle \ pi}$${\ displaystyle \ pi (i)}$${\ displaystyle \ pi (i)}$

${\ displaystyle r (i) ~~ = ~~ \ # \ {k \ mid k> i ~ \ land ~ \ pi (k) <\ pi (i) \}}$

Ambos e podem ser encontrados com a ajuda de um diagrama de Rothe , que é uma matriz de permutação com os 1s representados por pontos e uma inversão (frequentemente representada por uma cruz) em cada posição que tem um ponto à direita e abaixo dela. é a soma das inversões na linha do diagrama de Rothe, enquanto é a soma das inversões na coluna . A matriz de permutação da inversa é a transposta, portanto, de uma permutação é de sua inversa, e vice-versa. ${\ displaystyle v}$${\ displaystyle r}$${\ displaystyle r (i)}$${\ displaystyle i}$${\ displaystyle v (i)}$${\ displaystyle i}$${\ displaystyle v}$${\ displaystyle r}$

Exemplo: todas as permutações de quatro elementos

As seis inversões possíveis de uma permutação de 4 elementos

A tabela classificável a seguir mostra as 24 permutações de quatro elementos com seus conjuntos de inversão baseados em lugar, vetores relacionados à inversão e números de inversão. (As colunas pequenas são reflexos das colunas próximas a elas e podem ser usadas para classificá-las em ordem colexicográfica .)

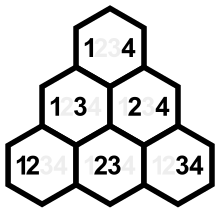
Pode-se observar que e sempre têm os mesmos dígitos, e que e estão ambos relacionados ao conjunto de inversão baseado em lugar. Os elementos não triviais de são as somas das diagonais descendentes do triângulo mostrado e os de são as somas das diagonais ascendentes. (Os pares nas diagonais descendentes têm os componentes direitos 2, 3, 4 em comum, enquanto os pares nas diagonais ascendentes têm os componentes esquerdos 1, 2, 3 em comum.) ${\ displaystyle v}$${\ displaystyle l}$${\ displaystyle l}$${\ displaystyle r}$${\ displaystyle l}$${\ displaystyle r}$

A ordem padrão da tabela é a ordem reversa do cólex por , que é o mesmo que a ordem do cólex por . Lex ordenar por é o mesmo que Lex ordenar por . ${\ displaystyle \ pi}$${\ displaystyle l}$${\ displaystyle \ pi}$${\ displaystyle r}$

Permutações de 3 elementos para comparação
0 1 2 3 4 5 ${\ displaystyle \ pi}$ ${\ displaystyle v}$ ${\ displaystyle l}$ pb ${\ displaystyle r}$ # 0 123 321 00 0 0 00 00 0 0 00 00 0 0 00 0 1 213 312 10 0 0 01 01 0 0 10 10 0 0 01 1 2 132 231 01 0 0 10 10 0 0 01 01 0 0 10 1 3 312 213 11 0 0 11 11 0 0 11 20 0 0 02 2 4 231 132 20 0 0 02 20 0 0 02 11 0 0 11 2 5 321 123 21 0 0 12 21 0 0 12 21 0 0 12 3

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23

${\ displaystyle \ pi}$ ${\ displaystyle v}$ ${\ displaystyle l}$ pb ${\ displaystyle r}$ # 0 1234 4321 000 0 0 000 000 0 0 000 000 0 0 000 0 1 2134 4312 100 0 0 001 001 0 0 100 100 0 0 001 1 2 1324 4231 010 0 0 010 010 0 0 010 010 0 0 010 1 3 3124 4213 110 0 0 011 011 0 0 110 200 0 0 002 2 4 2314 4132 200 0 0 002 020 0 0 020 110 0 0 011 2 5 3214 4123 210 0 0 012 021 0 0 120 210 0 0 012 3 6 1243 3421 001 0 0 100 100 0 0 001 001 0 0 100 1 7 2143 3412 101 0 0 101 101 0 0 101 101 0 0 101 2 8 1423 3241 011 0 0 110 110 0 0 011 020 0 0 020 2 9 4123 3214 111 0 0 111 111 0 0 111 300 0 0 003 3 10 2413 3142 201 0 0 102 120 0 0 021 120 0 0 021 3 11 4213 3124 211 0 0 112 121 0 0 121 310 0 0 013 4 12 1342 2431 020 0 0 020 200 0 0 002 011 0 0 110 2 13 3142 2413 120 0 0 021 201 0 0 102 201 0 0 102 3 14 1432 2341 021 0 0 120 210 0 0 012 021 0 0 120 3 15 4132 2314 121 0 0 121 211 0 0 112 301 0 0 103 4 16 3412 2143 220 0 0 022 220 0 0 022 220 0 0 022 4 17 4312 2134 221 0 0 122 221 0 0 122 320 0 0 023 5 18 2341 1432 300 0 0 003 300 0 0 003 111 0 0 111 3 19 3241 1423 310 0 0 013 301 0 0 103 211 0 0 112 4 20 2431 1342 301 0 0 103 310 0 0 013 121 0 0 121 4 21 4231 1324 311 0 0 113 311 0 0 113 311 0 0 113 5 22 3421 1243 320 0 0 023 320 0 0 023 221 0 0 122 5 23 4321 1234 321 0 0 123 321 0 0 123 321 0 0 123 6

Ordem fraca de permutações

Permutoedro do grupo simétrico S ₄

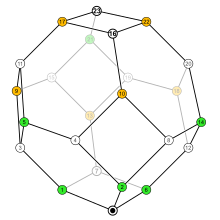
O conjunto de permutações em n itens pode receber a estrutura de uma ordem parcial , chamada de ordem fraca de permutações , que forma uma rede .

O diagrama de Hasse dos conjuntos de inversão ordenados pela relação de subconjunto forma o esqueleto de um permutoedro .

Se uma permutação é atribuída a cada conjunto de inversão usando a definição baseada no lugar, a ordem resultante das permutações é a do permutoedro, onde uma aresta corresponde à troca de dois elementos com valores consecutivos. Esta é a ordem fraca das permutações. A identidade é seu mínimo, e a permutação formada pela reversão da identidade é seu máximo.

Se uma permutação fosse atribuída a cada conjunto de inversão usando a definição baseada em elemento, a ordem resultante das permutações seria a de um gráfico de Cayley , onde uma aresta corresponde à troca de dois elementos em lugares consecutivos. Este gráfico de Cayley do grupo simétrico é semelhante ao seu permutoedro, mas com cada permutação substituída por seu inverso.

Veja também

• Sistema de número fatorial
• Gráfico de permutação
• Transposições, transposições simples, inversões e classificação
• Distância Damerau-Levenshtein
• Paridade de uma permutação

Sequências no OEIS :

• Sequências relacionadas à representação de base fatorial
• Números fatoriais: A007623 e A108731
• Números de inversão: A034968
• Conjuntos de inversão de permutações finitas interpretadas como números binários: A211362   (permutação relacionada: A211363 )
• Permutações finitas que têm apenas 0s e 1s em seus vetores de inversão: A059590   (seus conjuntos de inversão: A211364 )
• Número de permutações de n elementos com k inversões; Números maconianos: A008302   (seus máximos de linha; números Kendall-Mann: A000140 )
• Número de gráficos rotulados conectados com n arestas e n nós: A057500

Referências

Bibliografia fonte

Leitura adicional

Medidas de pré-ordenação