Teoria do nó - Knot theory

Exemplos de nós diferentes, incluindo o nó trivial (canto superior esquerdo) e o nó trifólio (abaixo dele)

Um diagrama de nó do nó trifólio, o nó não trivial mais simples

No campo matemático da topologia , a teoria dos nós é o estudo dos nós matemáticos . Embora seja inspirado por nós que aparecem na vida cotidiana, como os de cadarços e cordas, um nó matemático difere porque as pontas são unidas de forma que não pode ser desfeito, sendo o nó mais simples um anel (ou "desamarramento") . Em linguagem matemática, uma nó é uma incorporação de um círculo em três dimensões do espaço Euclidiano , (em topologia, um círculo não está ligado ao conceito geométrico clássica, mas para todas as suas Homeomorfismos ). Dois nós matemáticos são equivalentes se um pode ser transformado no outro por meio de uma deformação sobre si mesmo (conhecido como isotopia ambiental ); essas transformações correspondem a manipulações de um fio com nós que não envolvem cortá-lo ou passar por ele mesmo. ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle \ mathbb {R} ^ {3}}$

Os nós podem ser descritos de várias maneiras. Usando métodos de descrição diferentes, pode haver mais de uma descrição do mesmo nó. Por exemplo, um método comum para descrever um nó é um diagrama plano denominado diagrama de nó, no qual qualquer nó pode ser desenhado de muitas maneiras diferentes. Portanto, um problema fundamental na teoria do nó é determinar quando duas descrições representam o mesmo nó.

Existe uma solução algorítmica completa para este problema, que possui complexidade desconhecida . Na prática, os nós são freqüentemente distinguidos usando um invariante de nó , uma "quantidade" que é a mesma quando calculada a partir de diferentes descrições de um nó. Invariantes importantes incluem polinômios nó , grupos nó , e invariantes hiperbólicas.

A motivação original para os fundadores da teoria dos nós era criar uma tabela de nós e elos , que são nós de vários componentes emaranhados uns com os outros. Mais de seis bilhões de nós e links foram tabulados desde o início da teoria dos nós no século XIX.

Para obter mais informações, os matemáticos generalizaram o conceito de nó de várias maneiras. Os nós podem ser considerados em outros espaços tridimensionais e objetos diferentes de círculos podem ser usados; veja nó (matemática) . Os nós de dimensões superiores são esferas n- dimensionais no espaço euclidiano m- dimensional.

História

Trabalho de nós celtas intrincados no Livro de Kells de 1200 anos

Os arqueólogos descobriram que a amarração dos nós remonta aos tempos pré-históricos. Além de seus usos, como registrar informações e amarrar objetos, os nós têm interessado os humanos por sua estética e simbolismo espiritual. Os nós aparecem em várias formas de arte chinesa que datam de vários séculos aC (ver nó chinês ). O nó infinito aparece no budismo tibetano , enquanto os anéis borromeanos fizeram repetidas aparições em diferentes culturas, muitas vezes representando a força na unidade. Os monges celtas que criaram o Livro de Kells esbanjaram páginas inteiras com intrincados trabalhos de nós celtas .

O primeiro tabulador de nó, Peter Guthrie Tait

Uma teoria matemática dos nós foi desenvolvida pela primeira vez em 1771 por Alexandre-Théophile Vandermonde, que observou explicitamente a importância das características topológicas ao discutir as propriedades dos nós relacionadas à geometria da posição. Os estudos matemáticos de nós começaram no século 19 com Carl Friedrich Gauss , que definiu a integral de ligação ( Silver 2006 ). Na década de 1860, a teoria de Lord Kelvin de que os átomos eram nós no éter levou à criação de Peter Guthrie Tait das primeiras tabelas de nós para classificação completa. Tait, em 1885, publicou uma tabela de nós com até dez cruzamentos, e o que veio a ser conhecido como as conjecturas de Tait . Este registro motivou os primeiros teóricos do nó, mas a teoria do nó eventualmente se tornou parte do assunto emergente da topologia .

Esses topólogos do início do século 20 - Max Dehn , JW Alexander e outros - estudaram os nós do ponto de vista do grupo de nós e os invariantes da teoria da homologia , como o polinômio de Alexander . Essa seria a abordagem principal da teoria do nó até que uma série de avanços transformou o assunto.

No final dos anos 1970, William Thurston introduziu a geometria hiperbólica no estudo de nós com o teorema da hiperbolização . Muitos nós mostraram ser nós hiperbólicos , permitindo o uso da geometria na definição de invariantes de nó novos e poderosos . A descoberta do polinômio de Jones por Vaughan Jones em 1984 ( Sossinsky 2002 , pp. 71-89) e as contribuições subsequentes de Edward Witten , Maxim Kontsevich e outros revelaram profundas conexões entre a teoria do nó e métodos matemáticos em mecânica estatística e campo quântico teoria . Uma infinidade de invariantes de nó foi inventada desde então, utilizando ferramentas sofisticadas como grupos quânticos e homologia de Floer .

Nas últimas décadas do século 20, os cientistas começaram a se interessar pelo estudo dos nós físicos a fim de compreender o fenômeno dos nós no DNA e em outros polímeros. A teoria do nó pode ser usada para determinar se uma molécula é quiral (tem uma "lateralidade") ou não ( Simon 1986 ). Emaranhados , fios com ambas as extremidades fixadas no lugar, têm sido usados ​​com eficácia no estudo da ação da topoisomerase no DNA ( Flapan 2000 ). A teoria dos nós pode ser crucial na construção de computadores quânticos, por meio do modelo de computação quântica topológica ( Collins 2006 ).

Equivalência de nó

À esquerda, o desatamento e um nó equivalente a ele. Pode ser mais difícil determinar se nós complexos, como o da direita, são equivalentes ao nó desfeito.

Um nó é criado começando com um segmento de linha unidimensional , envolvendo-o em torno de si mesmo arbitrariamente e, em seguida, fundindo suas duas extremidades livres para formar um loop fechado ( Adams 2004 ) ( Sossinsky 2002 ). Simplesmente, podemos dizer que um nó é uma "curva fechada simples" ou "curva de Jordan (fechada)" (ver Curva ) - isto é: uma função "quase" injetiva e contínua , com o único ser de "não-injetividade" . Os topologistas consideram os nós e outros enredamentos, como elos e tranças, equivalentes se o nó puder ser empurrado suavemente, sem se cruzar, para coincidir com outro nó. ${\ displaystyle K}$ ${\ displaystyle K \ dois pontos [0,1] \ to \ mathbb {R} ^ {3}}$${\ displaystyle K (0) = K (1)}$

A ideia de equivalência de nós é dar uma definição precisa de quando dois nós devem ser considerados iguais, mesmo quando posicionados de forma bastante diferente no espaço. Uma definição matemática formal é que dois nós são equivalentes se houver um homeomorfismo de preservação de orientação com . ${\ displaystyle K_ {1}, K_ {2}}$ ${\ displaystyle h \ colon \ mathbb {R} ^ {3} \ to \ mathbb {R} ^ {3}}$${\ displaystyle h (K_ {1}) = K_ {2}}$

Outra maneira de definir a equivalência de nós é que dois nós são equivalentes quando há uma família contínua de homeomorfismos do espaço sobre si mesma, de forma que o último deles carregue o primeiro nó no segundo nó. (Mais formalmente: Dois nós e são equivalentes se houver um mapeamento contínuo tal que a) para cada um dos mapeamentos que leva a é um homeomorfismo de sobre si mesmo; b) para todos ; ec) . Essa função é conhecida como isotopia ambiental .) ${\ displaystyle \ {h_ {t}: \ mathbb {R} ^ {3} \ rightarrow \ mathbb {R} ^ {3} \ \ mathrm {para} \ 0 \ leq t \ leq 1 \}}$${\ displaystyle K_ {1}}$${\ displaystyle K_ {2}}$${\ displaystyle H: \ mathbb {R} ^ {3} \ times [0,1] \ rightarrow \ mathbb {R} ^ {3}}$${\ displaystyle t \ in [0,1]}$${\ displaystyle x \ in \ mathbb {R} ^ {3}}$${\ displaystyle H (x, t) \ in \ mathbb {R} ^ {3}}$${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle H (x, 0) = x}$${\ displaystyle x \ in \ mathbb {R} ^ {3}}$${\ displaystyle H (K_ {1}, 1) = K_ {2}}$${\ displaystyle H}$

Essas duas noções de equivalência de nós concordam exatamente sobre quais nós são equivalentes: Dois nós que são equivalentes sob a definição de homeomorfismo de preservação de orientação também são equivalentes sob a definição de isotopia ambiental, porque qualquer homeomorfismo de preservação de orientação de si mesmo é o estágio final de um isotopia ambiente a partir da identidade. Por outro lado, dois nós equivalentes sob a definição de isotopia ambiental também são equivalentes sob a definição de homeomorfismo de preservação de orientação, porque o estágio (final) da isotopia de ambiente deve ser um homeomorfismo de preservação de orientação carregando um nó para o outro. ${\ displaystyle \ mathbb {R} ^ {3}}$${\ displaystyle t = 1}$

O problema básico da teoria dos nós, o problema do reconhecimento , é determinar a equivalência de dois nós. Algoritmos existem para resolver este problema, com o primeiro dado por Wolfgang Haken no final dos anos 1960 ( Hass 1998 ). No entanto, esses algoritmos podem consumir muito tempo, e uma questão importante na teoria é entender o quão difícil é esse problema ( Hass 1998 ). O caso especial de reconhecimento do desatamento , denominado problema do desatamento , é de particular interesse ( Hoste 2005 ). Em fevereiro de 2021, Marc Lackenby anunciou um novo algoritmo de reconhecimento sem nó que é executado em tempo quase polinomial .

Diagramas de nó

Uma maneira útil de visualizar e manipular nós é projetar o nó em um plano - pense no nó projetando uma sombra na parede. Uma pequena mudança na direção da projeção garantirá que seja um a um, exceto nos pontos duplos, chamados cruzamentos , onde a "sombra" do nó se cruza uma vez transversalmente ( Rolfsen 1976 ). A cada cruzamento, para poder recriar o nó original, deve-se distinguir o sobrecordo do subcordo. Isso geralmente é feito criando uma quebra no fio que fica por baixo. O diagrama resultante é uma curva plana imersa com os dados adicionais de qual fio está acima e abaixo em cada cruzamento. (Esses diagramas são chamados de diagramas de nó quando representam um nó e diagramas de ligação quando representam uma ligação .) Analogamente, superfícies com nós em 4 espaços podem ser relacionadas a superfícies imersas em 3 espaços.

Um diagrama reduzido é um diagrama de nó no qual não há cruzamentos redutíveis (também cruzamentos desnecessários ou removíveis ), ou no qual todos os cruzamentos redutíveis foram removidos. A projeção de pétalas é um tipo de projeção em que, ao invés de formarem pontos duplos, todos os fios do nó se encontram em um único ponto de cruzamento, a ele conectado por laços formando "pétalas" não aninhadas.

Reidemeister se move

Em 1927, trabalhando com esta forma diagramática de nós, JW Alexander e Garland Baird Briggs , e independentemente Kurt Reidemeister , demonstraram que dois diagramas de nós pertencentes ao mesmo nó podem ser relacionados por uma sequência de três tipos de movimentos no diagrama, mostrado abaixo . Essas operações, agora chamadas de movimentos Reidemeister , são:

Reidemeister se move

Tipo I	Tipo II
Tipo III

A prova de que diagramas de nós equivalentes são conectados por movimentos de Reidemeister depende de uma análise do que acontece sob a projeção plana do movimento levando um nó a outro. O movimento pode ser organizado de modo que quase todo o tempo a projeção seja um diagrama de nós, exceto em muitas vezes quando um "evento" ou "catástrofe" ocorre, como quando mais de dois fios se cruzam em um ponto ou vários fios torne-se tangente em um ponto. Uma inspeção detalhada mostrará que eventos complicados podem ser eliminados, deixando apenas os eventos mais simples: (1) uma "torção" se formando ou sendo corrigida; (2) dois fios se tornando tangentes em um ponto e passando por ele; e (3) três fios se cruzando em um ponto. Esses são precisamente os movimentos de Reidemeister ( Sossinsky 2002 , cap. 3) ( Lickorish 1997 , cap. 1).

Invariantes de nó

Um invariante de nó é uma "quantidade" que é a mesma para nós equivalentes ( Adams 2004 ) ( Lickorish 1997 ) ( Rolfsen 1976 ). Por exemplo, se o invariante é calculado a partir de um diagrama de nós, ele deve fornecer o mesmo valor para dois diagramas de nós representando nós equivalentes. Um invariante pode assumir o mesmo valor em dois nós diferentes, portanto, por si só, pode ser incapaz de distinguir todos os nós. Uma invariante elementar é a tricolorabilidade .

Invariantes de nó "clássicos" incluem o grupo de nó , que é o grupo fundamental do complemento de nó , e o polinômio de Alexander , que pode ser calculado a partir do invariante de Alexander, um módulo construído a partir da cobertura cíclica infinita do complemento de nó ( Lickorish 1997 ) ( Rolfsen 1976 ). No final do século 20, invariantes como polinômios de nós "quânticos", invariantes de Vassiliev e invariantes hiperbólicos foram descobertos. Esses invariantes mencionados são apenas a ponta do iceberg da moderna teoria dos nós.

Polinômios de nó

Um polinômio de nó é um invariante de nó que é um polinômio . Exemplos bem conhecidos incluem os polinômios de Jones e Alexander . Uma variante do polinômio de Alexander, o polinômio de Alexander-Conway , é um polinômio na variável z com coeficientes inteiros ( Lickorish 1997 ).

O polinômio de Alexander-Conway é realmente definido em termos de links , que consistem em um ou mais nós emaranhados uns com os outros. Os conceitos explicados acima para nós, por exemplo, diagramas e movimentos Reidemeister, também são válidos para links.

Considere um diagrama de link orientado, ou seja , aquele em que cada componente do link tem uma direção preferencial indicada por uma seta. Para um dado cruzamento do diagrama, sejam os diagramas de links orientados resultantes da alteração do diagrama conforme indicado na figura: ${\ displaystyle L _ {+}, L _ {-}, L_ {0}}$

O diagrama original pode ser ou , dependendo da configuração da travessia escolhida. Em seguida, o polinômio de Alexander-Conway,, é recursivamente definido de acordo com as regras: ${\ displaystyle L _ {+}}$${\ displaystyle L _ {-}}$${\ displaystyle C (z)}$

• ${\ displaystyle C (O) = 1}$(onde está qualquer diagrama do unknot )${\ displaystyle O}$
• ${\ displaystyle C (L _ {+}) = C (L _ {-}) + zC (L_ {0}).}$

A segunda regra é frequentemente chamada de relação de novelo . Para verificar se essas regras fornecem uma invariante de um link orientado, deve-se determinar que o polinômio não muda sob os três movimentos de Reidemeister. Muitos polinômios de nó importantes podem ser definidos dessa maneira.

O seguinte é um exemplo de um cálculo típico usando uma relação de novelo. Ele calcula o polinômio de Alexander-Conway do nó trifólio . As manchas amarelas indicam onde a relação é aplicada.

C ( ) =  C ( ) +  z C ( )

fornece o unknot e o link Hopf . Aplicando a relação ao link Hopf onde indicado,

C ( ) = C ( ) + z C ( )

dá um link deformável para um com 0 cruzamentos (na verdade é o desvinculação de dois componentes) e um unknot. A desvinculação é um pouco furtiva:

C ( ) = C ( ) + z C ( )

o que implica que C (desvinculação de dois componentes) = 0, uma vez que os dois primeiros polinômios são do não nó e, portanto, iguais.

Juntar tudo isso mostrará:

${\ displaystyle C (\ mathrm {trevo}) = 1 + z (0 + z) = 1 + z ^ {2}}$

Uma vez que o polinômio de Alexander-Conway é um nó invariante, isso mostra que o trifólio não é equivalente ao desnó. Portanto, o trifólio é realmente "nodoso".

• 

  O nó trifólio canhoto.

• 

  O nó trifólio destro.

Na verdade, existem dois nós do trifólio, chamados de trifólio direito e esquerdo, que são imagens espelhadas um do outro (pegue um diagrama do trifólio dado acima e mude cada cruzamento para o outro para obter a imagem no espelho). Não são equivalentes entre si, o que significa que não são anfiquirais. Isso foi mostrado por Max Dehn , antes da invenção dos polinômios de nó, usando métodos teóricos de grupo ( Dehn 1914 ). Mas o polinômio de Alexander-Conway de cada tipo de trevo será o mesmo, como pode ser visto ao fazer o cálculo acima com a imagem espelhada. O polinômio de Jones pode de fato distinguir entre os nós do trifólio canhotos e destros ( Lickorish 1997 ).

Invariantes hiperbólicos

William Thurston provou que muitos nós são nós hiperbólicos , o que significa que o complemento do nó (isto é, o conjunto de pontos do espaço 3 não no nó) admite uma estrutura geométrica, em particular a da geometria hiperbólica . A estrutura hiperbólica depende apenas do nó, portanto, qualquer quantidade calculada a partir da estrutura hiperbólica é, então, um nó invariante ( Adams 2004 ).

Os anéis borromeanos são um elo com a propriedade de que remover um anel desvincula os outros.

Vista da cúspide de SnapPea : os anéis borromeanos se complementam na perspectiva de um habitante que vive próximo ao componente vermelho.

A geometria nos permite visualizar como é o interior de um nó ou complemento de link, imaginando os raios de luz viajando ao longo da geodésica da geometria. Um exemplo é fornecido pela imagem do complemento dos anéis borromeanos . O habitante deste complemento de link está visualizando o espaço próximo ao componente vermelho. As bolas na imagem são vistas dos bairros horoball do link. Ao engrossar o link de forma padrão, as vizinhanças horoball dos componentes do link são obtidas. Mesmo que o limite de uma vizinhança seja um toro, quando visto de dentro do complemento do link, ele se parece com uma esfera. Cada componente de link mostra infinitas esferas (de uma cor), pois há infinitos raios de luz do observador para o componente de link. O paralelogramo fundamental (que é indicado na imagem), ladrilhos vertical e horizontalmente e mostra como estender o padrão de esferas infinitamente.

Esse padrão, o padrão horoball, é em si um invariante útil. Outros invariantes hiperbólicos incluem a forma do paralelogramo fundamental, o comprimento da geodésica mais curta e o volume. Os esforços modernos de tabulação de nós e links têm utilizado esses invariantes de forma eficaz. Computadores rápidos e métodos inteligentes de obtenção desses invariantes tornam o cálculo desses invariantes, na prática, uma tarefa simples ( Adams, Hildebrand & Weeks 1991 ).

Dimensões superiores

Um nó em três dimensões pode ser desamarrado quando colocado no espaço quadridimensional. Isso é feito mudando os cruzamentos. Suponha que um fio esteja atrás de outro, visto de um ponto escolhido. Eleve-o até a quarta dimensão, para que não haja nenhum obstáculo (o fio dianteiro não tendo nenhum componente ali); em seguida, deslize-o para a frente e deixe-o cair para trás, agora na frente. As analogias para o avião seriam levantar uma corda da superfície ou remover um ponto de dentro de um círculo.

Na verdade, em quatro dimensões, qualquer loop fechado sem interseção de uma corda unidimensional é equivalente a um nó desfeito. Primeiro, "empurre" o loop para um subespaço tridimensional, o que sempre é possível, embora seja técnico de explicar.

Esferas de nó de dimensão superior

Uma vez que um nó pode ser considerado topologicamente uma esfera unidimensional, a próxima generalização é considerar uma esfera bidimensional ( ) embutida no espaço euclidiano de 4 dimensões ( ). Tal incorporação é atada se não houver homeomorfismo de sobre si mesma levando a 2-esfera incorporada à incorporação "redonda" padrão da 2-esfera. Nós suspensos e nós girados são duas famílias típicas desses nós de 2 esferas. ${\ displaystyle \ mathbb {S} ^ {2}}$${\ displaystyle \ mathbb {R} ^ {4}}$${\ displaystyle \ mathbb {R} ^ {4}}$

A técnica matemática chamada "posição geral" implica que para uma dada n -sfera no espaço euclidiano m- dimensional, se m for grande o suficiente (dependendo de n ), a esfera deve ser desatada. Em geral, n- esferas lineares por partes formam nós apenas no espaço ( n  + 2) -dimensional ( Zeeman 1963 ), embora isso não seja mais um requisito para esferas com nós suavemente. Na verdade, existem esferas suavemente atadas no espaço dimensional de 6 k ; por exemplo, há uma 3-esfera suavemente atada em ( Haefliger 1962 ) ( Levine 1965 ). Assim, a codimensão de um nó liso pode ser arbitrariamente grande quando não fixa a dimensão da esfera com nó; no entanto, qualquer k -sfera suave embutida com não tem nós. A noção de um nó tem mais generalizações em matemática, consulte: Nó (matemática) , classificação de isotopia de embeddings . ${\ displaystyle (4k-1)}$${\ displaystyle \ mathbb {R} ^ {6}}$${\ displaystyle \ mathbb {R} ^ {n}}$${\ displaystyle 2n-3k-3> 0}$

Cada nó na n -sfera é o elo de um conjunto real-algébrico com singularidade isolada em ( Akbulut & King 1981 ). ${\ displaystyle \ mathbb {S} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {n + 1}}$

Um n- nó é um único incorporado . Um n- link consiste em k -copias de embutidas em , onde k é um número natural . Os casos e os casos são bem estudados e, portanto, é o caso. ${\ displaystyle \ mathbb {S} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {m}}$${\ displaystyle \ mathbb {S} ^ {n}}$${\ displaystyle \ mathbb {R} ^ {m}}$${\ displaystyle m = n + 2}$${\ displaystyle m> n + 2}$${\ displaystyle n> 1}$

Adicionando nós

Adicionando dois nós

Dois nós podem ser adicionados cortando ambos os nós e juntando os pares de pontas. A operação é chamada de soma de nós , ou às vezes a soma conectada ou composição de dois nós. Isso pode ser definido formalmente da seguinte forma ( Adams 2004 ): considere uma projeção plana de cada nó e suponha que essas projeções sejam disjuntas. Encontre um retângulo no plano onde um par de lados opostos são arcos ao longo de cada nó, enquanto o resto do retângulo é separado dos nós. Forme um novo nó excluindo o primeiro par de lados opostos e juntando o outro par de lados opostos. O nó resultante é a soma dos nós originais. Dependendo de como isso é feito, dois nós diferentes (mas não mais) podem resultar. Esta ambigüidade na soma pode ser eliminada em relação aos nós como orientados , isto é, tendo uma direção preferencial de deslocamento ao longo do nó, e exigindo que os arcos dos nós na soma sejam orientados de forma consistente com o limite orientado do retângulo.

A soma dos nós orientados é comutativa e associativa . Um nó é primo se não for trivial e não puder ser escrito como a soma de dois nós não triviais. Um nó que pode ser escrito como tal soma é composto . Há uma decomposição primária para nós, análoga aos números primos e compostos ( Schubert 1949 ). Para nós orientados, essa decomposição também é única. Nós de dimensões mais altas também podem ser adicionados, mas existem algumas diferenças. Embora você não possa formar o desatamento em três dimensões adicionando dois nós não triviais, você pode fazer em dimensões superiores, pelo menos quando se considera nós suaves na codimensão pelo menos 3.

Nós tabulando

Uma mesa de nós principais até sete travessias. Os nós são rotulados com a notação Alexander – Briggs

Tradicionalmente, os nós são catalogados em termos de número de cruzamento . As tabelas de nós geralmente incluem apenas nós primos e apenas uma entrada para um nó e sua imagem espelhada (mesmo que sejam diferentes) ( Hoste, Thistlethwaite & Weeks 1998 ). O número de nós não triviais de um determinado número de cruzamento aumenta rapidamente, tornando a tabulação computacionalmente difícil ( Hoste 2005 , p. 20). Os esforços de tabulação conseguiram enumerar mais de 6 bilhões de nós e links ( Hoste 2005 , p. 28). A sequência do número de nós principais de um determinado número de cruzamento, até o número de cruzamento 16, é 0, 0, 1, 1, 2, 3, 7, 21, 49, 165, 552, 2176, 9988,46 972 ,253 293 ,1 388 705 ... (sequência A002863 no OEIS ). Embora os limites superior e inferior exponenciais para esta sequência sejam conhecidos, não foi provado que esta sequência seja estritamente crescente ( Adams 2004 ).

As primeiras tabelas de nós de Tait, Little e Kirkman usavam diagramas de nós, embora Tait também tenha usado um precursor da notação Dowker . Diferentes notações foram inventadas para nós que permitem uma tabulação mais eficiente ( Hoste 2005 ).

As primeiras tabelas tentaram listar todos os nós de no máximo 10 cruzamentos e todos os nós alternados de 11 cruzamentos ( Hoste, Thistlethwaite & Weeks 1998 ). O desenvolvimento da teoria do nó devido a Alexander, Reidemeister, Seifert e outros facilitou a tarefa de verificação e tabelas de nós até e incluindo 9 cruzamentos foram publicadas por Alexander – Briggs e Reidemeister no final dos anos 1920.

A primeira grande verificação desse trabalho foi feita na década de 1960 por John Horton Conway , que não apenas desenvolveu uma nova notação, mas também o polinômio de Alexander-Conway ( Conway 1970 ) ( Doll & Hoste 1991 ). Isso verificou a lista de nós de no máximo 11 travessias e uma nova lista de links de até 10 travessias. Conway encontrou várias omissões, mas apenas uma duplicação nas tabelas Tait-Little; no entanto, ele perdeu as duplicatas chamadas de par Perko , que só seriam notadas em 1974 por Kenneth Perko ( Perko 1974 ). Este famoso erro se propagou quando Dale Rolfsen adicionou uma mesa de nós em seu influente texto, baseado no trabalho de Conway. O artigo de Conway de 1970 sobre a teoria dos nós também contém uma duplicação tipográfica em sua página não alternada de 11 nós cruzados e omite 4 exemplos - 2 listados anteriormente na tese sênior de Princeton de D. Lombardero em 1968 e 2 outros posteriormente descobertos por Alain Caudron . [ver Perko (1982), Primality of sure knots, Topology Proceedings] Menos famosa é a duplicata em sua tabela de 10 elos de cruzamento: 2.-2.-20.20 é o espelho de 8 * -20: -20. [Ver Perko (2016), destaques históricos da teoria do nó não cíclico, J. Knot Theory Ramifications].

No final da década de 1990, Hoste, Thistlethwaite e Weeks tabularam todos os nós por meio de 16 cruzamentos ( Hoste, Thistlethwaite & Weeks 1998 ). Em 2003, Rankin, Flint e Schermann tabularam os nós alternados por meio de 22 cruzamentos ( Hoste 2005 ).

Notação Alexander – Briggs

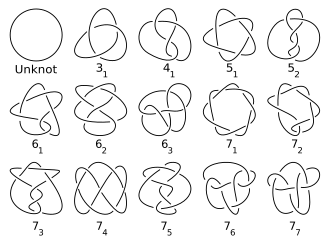
Esta é a notação mais tradicional, devido ao artigo de 1927 de James W. Alexander e Garland B. Briggs e posteriormente estendida por Dale Rolfsen em sua tabela de nós (ver imagem acima e Lista de nós principais ). A notação simplesmente organiza os nós por seu número de cruzamento. Um escreve o número de cruzamento com um subscrito para denotar sua ordem entre todos os nós com aquele número de cruzamento. Essa ordem é arbitrária e, portanto, não tem significado especial (embora em cada número de cruzamentos o nó torcido venha depois do nó toróide ). Os links são escritos pelo número de cruzamento com um sobrescrito para denotar o número de componentes e um subscrito para denotar sua ordem dentro dos links com o mesmo número de componentes e cruzamentos. Assim, o nó trifólio é notado 3 ₁ e a ligação Hopf é 2²
₁. Os nomes de Alexander-Briggs no intervalo de 10 ₁₆₂ a 10 ₁₆₆ são ambíguos, devido à descoberta do par Perko nas tabelas de nós originais e subsequentes de Charles Newton Little e diferenças na abordagem para corrigir este erro nas tabelas de nós e outras publicações criadas após este ponto.

Notação Dowker-Thistlethwaite

Um diagrama de nós com cruzamentos marcados para uma sequência Dowker

A notação Dowker-Thistlethwaite , também chamada de notação ou código Dowker, pois um nó é uma sequência finita de inteiros pares. Os números são gerados seguindo o nó e marcando os cruzamentos com inteiros consecutivos. Uma vez que cada cruzamento é visitado duas vezes, isso cria um emparelhamento de inteiros pares com inteiros ímpares. Um sinal apropriado é dado para indicar sobre e subcruzamento. Por exemplo, nesta figura o diagrama de nós tem cruzamentos rotulados com os pares (1,6) (3, −12) (5,2) (7,8) (9, −4) e (11, −10). A notação de Dowker-Thistlethwaite para esta rotulagem é a sequência: 6, −12, 2, 8, −4, −10. Um diagrama de nó tem mais de uma notação Dowker possível, e há uma ambigüidade bem compreendida ao reconstruir um nó a partir de uma notação Dowker – Thistlethwaite.

Notação de Conway

A notação de Conway para nós e elos, em homenagem a John Horton Conway , é baseada na teoria dos emaranhados ( Conway 1970 ). A vantagem dessa notação é que ela reflete algumas propriedades do nó ou elo.

A notação descreve como construir um diagrama de link específico do link. Comece com um poliedro básico , um gráfico planar conectado de 4 valências sem regiões digon . Esse poliedro é denotado primeiro pelo número de vértices e depois por um número de asteriscos que determinam a posição do poliedro em uma lista de poliedros básicos. Por exemplo, 10 ** denota o segundo poliedro de 10 vértices na lista de Conway.

Cada vértice tem então um emaranhado algébrico substituído nele (cada vértice é orientado de forma que não há escolha arbitrária na substituição). Cada um desses emaranhados tem uma notação que consiste em números e sinais + ou -.

Um exemplo é 1 * 2 −3 2. O 1 * denota o único poliedro básico de 1 vértice. O 2 −3 2 é uma sequência que descreve a fração contínua associada a um emaranhado racional . Insere-se este emaranhado no vértice do poliedro básico 1 *.

Um exemplo mais complicado é 8 * 3.1.2 0.1.1.1.1.1 Aqui, novamente, 8 * se refere a um poliedro básico com 8 vértices. Os pontos separam a notação para cada emaranhado.

Qualquer link admite tal descrição, e é claro que esta é uma notação muito compacta, mesmo para um número de cruzamento muito grande. Existem algumas outras abreviações geralmente usadas. O último exemplo é geralmente escrito 8 * 3: 2 0, onde os uns são omitidos e mantidos o número de pontos, exceto os pontos no final. Para um nó algébrico, como no primeiro exemplo, 1 * é freqüentemente omitido.

O artigo pioneiro de Conway sobre o assunto lista até poliedros básicos de 10 vértices, dos quais ele usa para tabular links, que se tornaram o padrão para esses links. Para uma lista adicional de poliedros de vértice superior, existem opções não padronizadas disponíveis.

Código de Gauss

O código de Gauss , semelhante à notação Dowker – Thistlethwaite, representa um nó com uma sequência de inteiros. No entanto, em vez de cada cruzamento ser representado por dois números diferentes, os cruzamentos são marcados com apenas um número. Quando o cruzamento é um overcrossing, um número positivo é listado. Em um cruzamento, um número negativo. Por exemplo, o nó do trevo no código de Gauss pode ser dado como: 1, −2,3, −1,2, −3

O código de Gauss é limitado em sua capacidade de identificar nós. Este problema é parcialmente resolvido com o código de Gauss estendido .

Veja também

• Topologia de circuito
• Geometria de contato # Subvariedades e nós de Legendrian
• Nós e gráficos
• Lista de tópicos da teoria do nó
• Nó molecular
• Topologia quântica
• Teoria da fita
• Gravata § Tipos de nó

Referências

Fontes

• Adams, Colin (2004), The Knot Book: An Elementary Introduction to the Mathematical Theory of Knots , American Mathematical Society , ISBN 978-0-8218-3678-1
• Adams, Colin ; Crawford, Thomas; DeMeo, Benjamin; Landry, Michael; Lin, Alex Tong; Montee, MurphyKate; Park, Seojung; Venkatesh, Saraswathi; Yhee, Farrah (2015), "Knot projections with a single multi-crossing", Journal of Knot Theory and its Ramifications , 24 (3): 1550011, 30, arXiv : 1208.5742 , doi : 10.1142 / S021821651550011X , MR  3342136
• Adams, Colin; Hildebrand, Martin; Weeks, Jeffrey (1991), "Hyperbolic invariants of knots and links", Transactions of the American Mathematical Society , 326 (1): 1-56, doi : 10.1090 / s0002-9947-1991-0994161-2 , JSTOR  2001854
• Akbulut, Selman ; King, Henry C. (1981), "All knots are algebraic", Comm. Matemática. Helv. , 56 (3): 339-351, doi : 10.1007 / BF02566217
• Bar-Natan, Dror (1995), "On the Vassiliev knot invariants", Topology , 34 (2): 423-472, doi : 10.1016 / 0040-9383 (95) 93237-2
• Collins, Graham (abril de 2006), "Computing with Quantum Knots", Scientific American , 294 (4), pp. 56-63, Bibcode : 2006SciAm.294d..56C , doi : 10.1038 / scientificamerican0406-56
• Dehn, Max (1914), "Die beiden Kleeblattschlingen", Mathematische Annalen , 75 : 402-413
• Conway, John Horton (1970), "Uma enumeração de nós e ligações, e algumas de suas propriedades algébricas", Computational Problems in Abstract Algebra , Pergamon, pp. 329-358, ISBN 978-0080129754, OCLC  322649
• Boneca, Helmut; Hoste, Jim (1991), "A tabulation of oriented links. With microfiche Supplement", Math. Comp. , 57 (196): 747–761, Bibcode : 1991MaCom..57..747D , doi : 10.1090 / S0025-5718-1991-1094946-4
• Flapan, Erica (2000), Quando a topologia encontra a química: Um olhar topológico na quiralidade molecular , Outlook, Cambridge University Press , ISBN 978-0-521-66254-3
• Haefliger, André (1962), "Knotted (4 k  - 1) -spheres in 6 k -space", Annals of Mathematics , Second Series, 75 (3): 452–466, doi : 10.2307 / 1970208 , JSTOR  1970208
• Hass, Joel (1998), "Algorithms for reconhecendo nós e 3-variedades", Chaos, Solitons and Fractals , 9 (4-5): 569-581, arXiv : math / 9712269 , Bibcode : 1998CSF ..... 9 ..569H , doi : 10.1016 / S0960-0779 (97) 00109-4
• Hoste, Jim; Thistlethwaite, Morwen ; Weeks, Jeffrey (1998), "The First 1.701.935 Knots", Math. Intelligencer , 20 (4): 33-48, doi : 10.1007 / BF03025227
• Hoste, Jim (2005), "A enumeração e classificação de nós e ligações", Handbook of Knot Theory (PDF) , Amsterdam: Elsevier
• Levine, Jerome (1965), "A classificação de nós diferenciáveis", Annals of Mathematics , Second Series, 1982 (1): 15–50, doi : 10.2307 / 1970561 , JSTOR  1970561
• Kontsevich, Maxim (1993), "Vassiliev's knot invariants", IM Gelfand Seminar, Adv. Matemática soviética. , 2, Providence, RI: American Mathematical Society, 16 : 137-150, doi : 10.1090 / advsov / 016.2 / 04 , ISBN 9780821841174
• Lickorish, WB Raymond (1997), An Introduction to Knot Theory , Graduate Texts in Mathematics, Springer-Verlag, ISBN 978-0-387-98254-0
• Perko, Kenneth (1974), "Sobre a classificação dos nós", Proceedings of the American Mathematical Society , 45 (2): 262–6, doi : 10.2307 / 2040074 , JSTOR  2040074
• Rolfsen, Dale (1976), Knots and Links , Mathematics Lecture Series, 7 , Berkeley, California : Publish or Perish, ISBN 978-0-914098-16-4, MR  0515288
• Schubert, Horst (1949), "Die eindeutige Zerlegbarkeit eines Knotens in Primknoten", Heidelberger Akad. Wiss. Math.-Nat. Kl. (3): 57-104
• Silver, Dan (2006), "Knot theory's odd origins" (PDF) , American Scientist , 94 (2), pp. 158-165, doi : 10.1511 / 2006.2.158
• Simon, Jonathan (1986), "Topological chirality of certas moléculas", Topology , 25 (2): 229-235, doi : 10.1016 / 0040-9383 (86) 90041-8
• Sossinsky, Alexei (2002), Knots, mathematics with a twist , Harvard University Press, ISBN 978-0-674-00944-8
• Turaev, VG (1994), "Quantum invariants of knots and 3-manifolds" , De Gruyter Studies in Mathematics , Berlin: Walter de Gruyter & Co., 18 , arXiv : hep-th / 9409028 , ISBN 978-3-11-013704-0
• Weisstein, Eric W. (2013). "Diagrama de Nó Reduzido" . MathWorld . Wolfram . Retirado em 8 de maio de 2013 .
• Weisstein, Eric W. (2013a). "Cruzamento Redutível" . MathWorld . Wolfram . Retirado em 8 de maio de 2013 .
• Witten, Edward (1989), "Quantum field theory and the Jones polynomial", Comm. Matemática. Phys. , 121 (3): 351-399, Bibcode : 1989CMaPh.121..351W , doi : 10.1007 / BF01217730
• Zeeman, EC (1963), "Unknotting combinatorial balls", Annals of Mathematics , Second Series, 78 (3): 501-526, doi : 10.2307 / 1970538 , JSTOR  1970538

Notas de rodapé

Leitura adicional

Livros didáticos introdutórios

Existem várias introduções à teoria do nó. Uma introdução clássica para alunos de pós-graduação ou alunos de graduação avançados é ( Rolfsen 1976 ). Outros bons textos das referências são ( Adams 2001 ) e ( Lickorish 1997 ). Adams é informal e acessível em sua maior parte para alunos do ensino médio. Lickorish é uma introdução rigorosa para alunos de pós-graduação, cobrindo uma bela mistura de tópicos clássicos e modernos. erro harv: sem alvo: CITEREFAdams2001 ( ajuda )

• Burde, Gerhard ; Zieschang, Heiner (1985), Knots , De Gruyter Studies in Mathematics, 5 , Walter de Gruyter, ISBN 978-3-11-008675-1
• Crowell, Richard H .; Fox, Ralph (1977). Introdução à teoria dos nós . ISBN 978-0-387-90272-2.
• Kauffman, Louis H. (1987), On Knots , ISBN 978-0-691-08435-0
• Kauffman, Louis H. (2013), Knots and Physics (4ª ed.), World Scientific, ISBN 978-981-4383-00-4

pesquisas

• Menasco, William W .; Thistlethwaite, Morwen , eds. (2005), Handbook of Knot Theory , Elsevier, ISBN 978-0-444-51452-3
  • O manual de Menasco e Thistlethwaite examina uma mistura de tópicos relevantes para as tendências de pesquisa atuais de uma maneira acessível para alunos de graduação avançados, mas de interesse para pesquisadores profissionais.
• Livio, Mario (2009), "Ch. 8: Unreasonable Effectiveness?" , Deus é um matemático? , Simon & Schuster, pp. 203-218, ISBN 978-0-7432-9405-8

links externos

• "Mathematics and Knots" Esta é uma versão online de uma exposição desenvolvida para a Royal Society "PopMath RoadShow" de 1989. Seu objetivo era usar nós para apresentar métodos matemáticos ao público em geral.

História

• Thomson, Sir William (1867), "On Vortex Atoms" , Proceedings of the Royal Society of Edinburgh , VI : 94-105
• Silliman, Robert H. (dezembro de 1963), "William Thomson: Smoke Rings and Nineteenth-Century Atomism", Isis , 54 (4): 461–474, doi : 10.1086 / 349764 , JSTOR  228151
• Filme de uma recriação moderna do experimento do anel de fumaça de Tait
• História da teoria do nó (na página inicial de Andrew Ranicki )

Tabelas Knot e software

• KnotInfo : Tabela de Invariantes de Nó e Recursos da Teoria de Nó
• The Knot Atlas - informações detalhadas sobre nós individuais em tabelas de nós
• KnotPlot - software para investigar propriedades geométricas de nós
• Knotscape - software para criar imagens de nós
• Knoutilus - banco de dados online e gerador de imagens de nós
• KnotData.html - função Wolfram Mathematica para investigar nós