Regressão logística - Logistic regression

Em estatística , o modelo logístico (ou modelo logit ) é usado para modelar a probabilidade de uma determinada classe ou evento existir, como aprovação / reprovação, vitória / derrota, vivo / morto ou saudável / doente. Isso pode ser estendido para modelar várias classes de eventos, como determinar se uma imagem contém um gato, cachorro, leão, etc. Cada objeto sendo detectado na imagem seria atribuído a uma probabilidade entre 0 e 1, com uma soma de um.

A regressão logística é um modelo estatístico que em sua forma básica usa uma função logística para modelar uma variável dependente binária , embora existam muitas extensões mais complexas . Na análise de regressão , a regressão logística (ou regressão logit ) estima os parâmetros de um modelo logístico (uma forma de regressão binária ). Matematicamente, um modelo logístico binário possui uma variável dependente com dois valores possíveis, como aprovação / reprovação, que é representada por uma variável indicadora , onde os dois valores são rotulados como "0" e "1". No modelo logístico, o log-odds (o logaritmo dos odds ) para o valor denominado "1" é uma combinação linear de uma ou mais variáveis ​​independentes ("preditores"); as variáveis ​​independentes podem ser, cada uma, uma variável binária (duas classes, codificadas por uma variável indicadora) ou uma variável contínua (qualquer valor real). A probabilidade correspondente do valor rotulado "1" pode variar entre 0 (certamente o valor "0") e 1 (certamente o valor "1"), daí a rotulagem; a função que converte log-odds em probabilidade é a função logística, daí o nome. A unidade de medida da escala log-odds é chamada logit , de log istic un it , daí os nomes alternativos. Modelos análogos com uma função sigmóide diferente em vez da função logística também podem ser usados, como o modelo probit ; a característica definidora do modelo logístico é que o aumento de uma das variáveis ​​independentes escala multiplicativamente as chances de um determinado resultado a uma taxa constante , com cada variável independente tendo seu próprio parâmetro; para uma variável dependente binária, isso generaliza a razão de chances .

Em um modelo de regressão logística binária, a variável dependente possui dois níveis ( categóricos ). As saídas com mais de dois valores são modeladas por regressão logística multinomial e, se as categorias múltiplas forem ordenadas , por regressão logística ordinal (por exemplo, o modelo logístico ordinal de odds proporcionais). O próprio modelo de regressão logística simplesmente modela a probabilidade de saída em termos de entrada e não realiza classificação estatística (não é um classificador), embora possa ser usado para fazer um classificador, por exemplo, escolhendo um valor de corte e classificando entradas com probabilidade maior do que o corte como uma classe, abaixo do corte como a outra; esta é uma maneira comum de fazer um classificador binário . Os coeficientes geralmente não são calculados por uma expressão de forma fechada, ao contrário dos mínimos quadrados lineares ; consulte § Ajuste do modelo . A regressão logística como um modelo estatístico geral foi originalmente desenvolvida e popularizada principalmente por Joseph Berkson , começando em Berkson (1944) , onde ele cunhou "logit"; veja § História . erro harvtxt: sem alvo: CITEREFBerkson1944 ( ajuda )

Parte de uma série sobre
Análise de regressão
Modelos
Regressão linear Regressão simples Regressão polinomial Modelo linear geral
Modelo linear generalizado Escolha discreta Regressão binomial Regressão binária Regressão logística Regressão logística multinomial Logit misto Probit Probit multinomial Logit ordenado Probit ordenado Poisson
Modelo multinível Efeitos fixos Efeitos aleatórios Modelo linear de efeitos mistos Modelo de efeitos mistos não linear
Regressão não linear Não paramétrico Semiparamétrico Robusto Quantil Isotônico Componentes principais Ângulo mínimo Local Segmentado
Erros em variáveis
Estimativa
Mínimos quadrados Linear Não linear
Ordinário Pesada Generalizado
Parcial Total Não negativo Regressão de cume Regularizado
Desvios mínimos absolutos Reponderado iterativamente Bayesiano Multivariada bayesiana
Fundo
Validação de regressão Resposta média e prevista Erros e residuais Qualidade de ajuste Resíduo estudantizado Teorema de Gauss-Markov
Portal de matemática
v t e

Formulários

A regressão logística é usada em vários campos, incluindo aprendizado de máquina, a maioria dos campos médicos e ciências sociais. Por exemplo, o Trauma and Injury Severity Score ( TRISS ), amplamente utilizado para predizer mortalidade em pacientes feridos, foi originalmente desenvolvido por Boyd et al. usando regressão logística. Muitas outras escalas médicas usadas para avaliar a gravidade de um paciente foram desenvolvidas por meio de regressão logística. A regressão logística pode ser usada para prever o risco de desenvolver uma determinada doença (por exemplo, diabetes ; doença coronariana ), com base nas características observadas do paciente (idade, sexo, índice de massa corporal , resultados de vários exames de sangue , etc.). Outro exemplo pode ser prever se um eleitor nepalês votará no Congresso do Nepal ou no Partido Comunista do Nepal ou em qualquer outro partido, com base na idade, renda, sexo, raça, estado de residência, votos em eleições anteriores, etc. A técnica também pode ser usado em engenharia , especialmente para prever a probabilidade de falha de um determinado processo, sistema ou produto. Ele também é usado em aplicativos de marketing , como previsão da propensão de um cliente para comprar um produto ou interromper uma assinatura, etc. Em economia , pode ser usado para prever a probabilidade de uma pessoa acabar na força de trabalho, e um aplicativo de negócios faria ser para prever a probabilidade de um proprietário inadimplente em uma hipoteca . Os campos aleatórios condicionais , uma extensão da regressão logística para dados sequenciais, são usados ​​no processamento de linguagem natural .

Exemplos

Modelo logístico

Vamos tentar entender a regressão logística considerando um modelo logístico com parâmetros dados, então vendo como os coeficientes podem ser estimados a partir dos dados. Considere um modelo com dois preditores e , e uma variável de resposta binária (Bernoulli) , que denotamos . Assumimos uma relação linear entre as variáveis ​​preditoras e as probabilidades de log (também chamadas de logit) do evento que . Esta relação linear pode ser escrita na seguinte forma matemática (onde ℓ é o log-odds, é a base do logaritmo e são parâmetros do modelo): ${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle Y}$${\ displaystyle p = P (Y = 1)}$${\ displaystyle Y = 1}$${\ displaystyle b}$${\ displaystyle \ beta _ {i}}$

${\ displaystyle \ ell = \ log _ {b} {\ frac {p} {1-p}} = \ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2}}$

Podemos recuperar as probabilidades exponenciando as probabilidades logarítmicas:

${\ displaystyle {\ frac {p} {1-p}} = b ^ {\ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2}}}$.

Por manipulação simples algébrico (e dividindo numerador e denominador por ), a probabilidade de que é ${\ displaystyle b ^ {\ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2}}}$${\ displaystyle Y = 1}$

${\ displaystyle p = {\ frac {b ^ {\ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2}}} {b ^ {\ beta _ { 0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2}} + 1}} = {\ frac {1} {1 + b ^ {- (\ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2})}}} = S_ {b} (\ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2})}$.

Onde está a função sigmóide com base . A fórmula acima mostra que, uma vez que são fixos, podemos facilmente calcular as probabilidades logarítmicas de uma dada observação ou a probabilidade de uma determinada observação. O principal caso de uso de um modelo logístico é receber uma observação e estimar a probabilidade disso . Na maioria das aplicações, a base do logaritmo geralmente é considerada e . No entanto, em alguns casos, pode ser mais fácil comunicar os resultados trabalhando na base 2 ou 10. ${\ displaystyle S_ {b}}$${\ displaystyle b}$${\ displaystyle \ beta _ {i}}$${\ displaystyle Y = 1}$${\ displaystyle Y = 1}$${\ displaystyle (x_ {1}, x_ {2})}$${\ displaystyle p}$${\ displaystyle Y = 1}$${\ displaystyle b}$

Nós consideramos um exemplo com e coeficientes , e . Para ser concreto, o modelo é ${\ displaystyle b = 10}$${\ displaystyle \ beta _ {0} = - 3}$${\ displaystyle \ beta _ {1} = 1}$${\ displaystyle \ beta _ {2} = 2}$

${\ displaystyle \ log _ {10} {\ frac {p} {1-p}} = \ ell = -3 + x_ {1} + 2x_ {2}}$

onde está a probabilidade do evento que . ${\ displaystyle p}$${\ displaystyle Y = 1}$

Isso pode ser interpretado da seguinte forma:

• ${\ displaystyle \ beta _ {0} = - 3}$é a interceptação y . É o log-odds do evento que , quando os preditores . Ao exponenciar, podemos ver que quando as chances do evento são de 1 para 1000, ou . Da mesma forma, a probabilidade do evento que , quando pode ser calculado como .${\ displaystyle Y = 1}$${\ displaystyle x_ {1} = x_ {2} = 0}$${\ displaystyle x_ {1} = x_ {2} = 0}$${\ displaystyle Y = 1}$${\ displaystyle 10 ^ {- 3}}$${\ displaystyle Y = 1}$${\ displaystyle x_ {1} = x_ {2} = 0}$${\ displaystyle 1 / (1000 + 1) = 1/1001}$
• ${\ displaystyle \ beta _ {1} = 1}$significa que aumentar em 1 aumenta as chances de log em . Portanto, se aumentar em 1, as chances aumentam em um fator de . Observe que a probabilidade de também aumentou, mas não aumentou tanto quanto as chances aumentaram.${\ displaystyle x_ {1}}$${\ displaystyle 1}$${\ displaystyle x_ {1}}$${\ displaystyle Y = 1}$${\ displaystyle 10 ^ {1}}$${\ displaystyle Y = 1}$
• ${\ displaystyle \ beta _ {2} = 2}$significa que aumentar em 1 aumenta as chances de log em . Portanto, se aumenta em 1, as probabilidades aumentam por um fator de Observe como o efeito de nas probabilidades logarítmicas é duas vezes maior do que o efeito de , mas o efeito nas probabilidades é 10 vezes maior. Mas o efeito na probabilidade de não é tão 10 vezes maior, é apenas o efeito nas probabilidades que é 10 vezes maior.${\ displaystyle x_ {2}}$${\ displaystyle 2}$${\ displaystyle x_ {2}}$${\ displaystyle Y = 1}$${\ displaystyle 10 ^ {2}.}$${\ displaystyle x_ {2}}$${\ displaystyle x_ {1}}$${\ displaystyle Y = 1}$

Para estimar os parâmetros dos dados, deve-se fazer uma regressão logística. ${\ displaystyle \ beta _ {i}}$

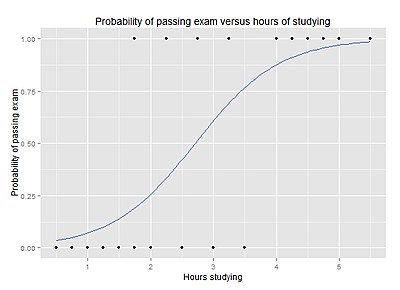
Probabilidade de passar em um exame versus horas de estudo

Para responder à seguinte pergunta:

Um grupo de 20 alunos gasta entre 0 e 6 horas estudando para um exame. Como o número de horas gastas estudando afeta a probabilidade de o aluno ser aprovado no exame?

A razão para usar a regressão logística para este problema é que os valores da variável dependente, passa e falha, embora representados por "1" e "0", não são números cardinais . Se o problema foi alterado de forma que aprovação / reprovação foi substituído pela nota 0–100 (números cardinais), então a análise de regressão simples pode ser usada.

A tabela mostra o número de horas que cada aluno passou estudando e se eles foram aprovados (1) ou reprovados (0).

Horas	0,50	0,75	1,00	1,25	1,50	1,75	1,75	2,00	2,25	2,50	2,75	3,00	3,25	3,50	4,00	4,25	4,50	4,75	5,00	5,50
Passar	0	0	0	0	0	0	1	0	1	0	1	0	1	0	1	1	1	1	1	1

O gráfico mostra a probabilidade de aprovação no exame versus o número de horas de estudo, com a curva de regressão logística ajustada aos dados.

A análise de regressão logística fornece a seguinte saída.

	Coeficiente	Std.Error	valor z	Valor P (Wald)
Interceptar	-4,0777	1,7610	-2,316	0,0206
Horas	1,5046	0,6287	2.393	0,0167

A saída indica que as horas de estudo estão significativamente associadas à probabilidade de passar no exame ( , teste de Wald ). A saída também fornece os coeficientes para e . Esses coeficientes são inseridos na equação de regressão logística para estimar as chances (probabilidade) de passar no exame: ${\ displaystyle p = 0,0167}$${\ displaystyle {\ text {Intercept}} = - 4.0777}$${\ displaystyle {\ text {Horas}} = 1,5046}$

${\ displaystyle {\ begin {align} {\ text {Log-odds of passar exam}} & = 1,5046 \ cdot {\ text {Hours}} - 4,0777 = 1,5046 \ cdot ({\ text {Hours}} - 2,71) \\ {\ text {Probabilidade de passar no exame}} & = \ exp \ left (1.5046 \ cdot {\ text {Horas}} - 4.0777 \ right) = \ exp \ left (1.5046 \ cdot ({\ text {Horas} } -2.71) \ right) \\ {\ text {Probabilidade de passar no exame}} & = {\ frac {1} {1+ \ exp \ left (- \ left (1.5046 \ cdot {\ text {Horas}} - 4.0777 \ right) \ right)}} \ end {alinhado}}}$

Estima-se que uma hora adicional de estudo aumente as probabilidades logarítmicas de passar em 1,5046, portanto, multiplicar as probabilidades de passar pelo formulário com o intercepto x (2,71) mostra que isso estima as probabilidades pares ( probabilidades logarítmicas 0, probabilidades 1, probabilidade 1 / 2) para um aluno que estuda 2,71 horas. ${\ displaystyle \ exp (1.5046) \ aproximadamente 4.5.}$

Por exemplo, para um aluno que estuda 2 horas, inserir o valor na equação dá a probabilidade estimada de aprovação no exame de 0,26: ${\ displaystyle {\ text {Horas}} = 2}$

${\ displaystyle {\ text {Probabilidade de passar no exame}} = {\ frac {1} {1+ \ exp \ left (- \ left (1.5046 \ cdot 2-4.0777 \ right) \ right)}} = 0.26}$

Da mesma forma, para um aluno que estuda 4 horas, a probabilidade estimada de aprovação no exame é de 0,87:

${\ displaystyle {\ text {Probabilidade de passar no exame}} = {\ frac {1} {1+ \ exp \ left (- \ left (1.5046 \ cdot 4-4.0777 \ right) \ right)}} = 0,87}$

Esta tabela mostra a probabilidade de aprovação no exame para vários valores de horas de estudo.

Horas de estudo	Passando no exame
	Log-odds	Chances	Probabilidade
1	-2,57	0,076 ≈ 1: 13,1	0,07
2	-1,07	0,34 ≈ 1: 2,91	0,26
3	0,44	1,55	0,61
4	1,94	6,96	0,87
5	3,45	31,4	0,97

A saída da análise de regressão logística fornece um valor p de , que é baseado no escore z de Wald. Em vez do método de Wald, o método recomendado para calcular o valor p para regressão logística é o teste da razão de verossimilhança (LRT), que para esses dados dá . ${\ displaystyle p = 0,0167}$${\ displaystyle p = 0,0006}$

Discussão

A regressão logística pode ser binomial, ordinal ou multinomial. A regressão logística binomial ou binária lida com situações em que o resultado observado para uma variável dependente pode ter apenas dois tipos possíveis, "0" e "1" (que pode representar, por exemplo, "passa" vs. "falha" ou "ganha "vs." perda "). A regressão logística multinomial lida com situações em que o resultado pode ter três ou mais tipos possíveis (por exemplo, "doença A" vs. "doença B" vs. "doença C") que não são ordenados. A regressão logística ordinal lida com variáveis ​​dependentes que são ordenadas.

Na regressão logística binária, o resultado é geralmente codificado como "0" ou "1", pois isso leva à interpretação mais direta. Se um determinado resultado observado para a variável dependente é o resultado possível digno de nota (referido como um "sucesso" ou uma "instância" ou um "caso"), é geralmente codificado como "1" e o resultado contrário (referido como um "falha" ou "não instância" ou "não caso") como "0". A regressão logística binária é usada para prever as chances de ser um caso com base nos valores das variáveis ​​independentes (preditores). As probabilidades são definidas como a probabilidade de que um determinado resultado seja um caso dividido pela probabilidade de que seja uma não ocorrência.

Como outras formas de análise de regressão , a regressão logística faz uso de uma ou mais variáveis ​​preditoras que podem ser contínuas ou categóricas. Ao contrário da regressão linear comum, no entanto, a regressão logística é usada para prever variáveis ​​dependentes que fazem parte de uma de um número limitado de categorias (tratando a variável dependente no caso binomial como o resultado de um ensaio de Bernoulli ) em vez de um resultado contínuo. Dada essa diferença, as premissas da regressão linear são violadas. Em particular, os resíduos não podem ser normalmente distribuídos. Além disso, a regressão linear pode fazer previsões sem sentido para uma variável dependente binária. O que é necessário é uma forma de converter uma variável binária em uma contínua que pode assumir qualquer valor real (negativo ou positivo). Para fazer isso, a regressão logística binomial primeiro calcula as chances de o evento acontecer para diferentes níveis de cada variável independente e, em seguida, usa seu logaritmo para criar um critério contínuo como uma versão transformada da variável dependente. O logaritmo das probabilidades é o logit da probabilidade, o logit é definido da seguinte forma:

${\ displaystyle \ operatorname {logit} p = \ ln {\ frac {p} {1-p}} \ quad {\ text {para}} 0 <p <1 \ ,.}$

Embora a variável dependente na regressão logística seja Bernoulli, o logit está em uma escala irrestrita. A função logit é a função de ligação neste tipo de modelo linear generalizado, ou seja,

${\ displaystyle \ operatorname {logit} \ operatorname {\ mathcal {E}} (Y) = \ beta _ {0} + \ beta _ {1} x}$

Y é a variável de resposta distribuída de Bernoulli e x é a variável preditora; os valores β são os parâmetros lineares.

O logit da probabilidade de sucesso é então ajustado aos preditores. O valor previsto do logit é convertido de volta em probabilidades previstas, por meio do inverso do logaritmo natural - a função exponencial . Assim, embora a variável dependente observada na regressão logística binária seja uma variável 0 ou 1, a regressão logística estima as chances, como uma variável contínua, de que a variável dependente seja um 'sucesso'. Em alguns aplicativos, as chances são tudo o que é necessário. Em outros, uma previsão específica do tipo sim ou não é necessária para determinar se a variável dependente é ou não um 'sucesso'; esta previsão categórica pode ser baseada nas probabilidades de sucesso computadas, com as probabilidades previstas acima de algum valor de corte escolhido sendo traduzidas em uma previsão de sucesso.

A suposição de efeitos de preditor linear pode ser facilmente relaxada usando técnicas como funções spline .

Regressão logística vs. outras abordagens

A regressão logística mede a relação entre a variável dependente categórica e uma ou mais variáveis ​​independentes, estimando probabilidades usando uma função logística , que é a função de distribuição cumulativa da distribuição logística . Assim, ele trata o mesmo conjunto de problemas que a regressão probit usando técnicas semelhantes, com a última usando uma curva de distribuição normal cumulativa. De forma equivalente, nas interpretações das variáveis ​​latentes desses dois métodos, o primeiro assume uma distribuição logística padrão de erros e o segundo uma distribuição normal padrão de erros.

A regressão logística pode ser vista como um caso especial do modelo linear generalizado e, portanto, análoga à regressão linear . O modelo de regressão logística, entretanto, é baseado em suposições bastante diferentes (sobre a relação entre as variáveis ​​dependentes e independentes) daquelas de regressão linear. Em particular, as principais diferenças entre esses dois modelos podem ser vistas nas seguintes duas características de regressão logística. Primeiro, a distribuição condicional é uma distribuição Bernoulli em vez de uma distribuição Gaussiana , porque a variável dependente é binária. Em segundo lugar, os valores previstos são probabilidades e, portanto, são restritos a (0,1) por meio da função de distribuição logística porque a regressão logística prevê a probabilidade de resultados específicos, em vez dos próprios resultados. ${\ displaystyle y \ mid x}$

A regressão logística é uma alternativa ao método de Fisher de 1936, a análise discriminante linear . Se as suposições da análise discriminante linear forem mantidas, o condicionamento pode ser revertido para produzir regressão logística. O inverso não é verdadeiro, entretanto, porque a regressão logística não requer a suposição normal multivariada da análise discriminante.

Interpretação de variável latente

A regressão logística pode ser entendida simplesmente como encontrar os parâmetros que melhor se ajustam: ${\ displaystyle \ beta}$

${\ displaystyle y = {\ begin {cases} 1 & \ beta _ {0} + \ beta _ {1} x + \ varepsilon> 0 \\ 0 & {\ text {else}} \ end {cases}}}$

onde é um erro distribuído pela distribuição logística padrão . (Se a distribuição normal padrão for usada em vez disso, é um modelo probit .) ${\ displaystyle \ varepsilon}$

A variável latente associada é . O termo de erro não é observado e , portanto, também é inobservável, portanto denominado "latente" (os dados observados são valores de e ). Ao contrário da regressão comum, no entanto, os parâmetros não podem ser expressos por nenhuma fórmula direta dos valores e nos dados observados. Em vez disso, eles devem ser encontrados por um processo de pesquisa iterativa, geralmente implementado por um programa de software, que encontra o máximo de uma "expressão de verossimilhança" complicada que é uma função de todos os valores e observados . A abordagem de estimativa é explicada abaixo. ${\ displaystyle y '= \ beta _ {0} + \ beta _ {1} x + \ varepsilon}$${\ displaystyle \ varepsilon}$${\ displaystyle y '}$${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle \ beta}$${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle x}$

Função logística, odds, odds ratio e logit

Definição da função logística

Uma explicação da regressão logística pode começar com uma explicação da função logística padrão . A função logística é uma função sigmóide , que recebe qualquer entrada real e produz um valor entre zero e um. Para o logit, isso é interpretado como obter log-odds de entrada e ter probabilidade de saída . A função logística padrão é definida da seguinte forma: ${\ displaystyle t}$${\ displaystyle \ sigma: \ mathbb {R} \ rightarrow (0,1)}$

${\ displaystyle \ sigma (t) = {\ frac {e ^ {t}} {e ^ {t} +1}} = {\ frac {1} {1 + e ^ {- t}}}}$

Um gráfico da função logística no intervalo t (−6,6) é mostrado na Figura 1.

Vamos supor que seja uma função linear de uma única variável explicativa (o caso em que é uma combinação linear de múltiplas variáveis ​​explicativas é tratado de forma semelhante). Podemos então expressar o seguinte: ${\ displaystyle t}$ ${\ displaystyle x}$${\ displaystyle t}$${\ displaystyle t}$

${\ displaystyle t = \ beta _ {0} + \ beta _ {1} x}$

E a função logística geral agora pode ser escrita como: ${\ displaystyle p: \ mathbb {R} \ rightarrow (0,1)}$

${\ displaystyle p (x) = \ sigma (t) = {\ frac {1} {1 + e ^ {- (\ beta _ {0} + \ beta _ {1} x)}}}}$

No modelo logístico, é interpretado como a probabilidade da variável dependente se igualar a um sucesso / caso em vez de uma falha / não caso. É claro que as variáveis ​​de resposta não são distribuídas de forma idêntica: difere de um ponto de dados para outro, embora sejam independentes, dada a matriz de design e os parâmetros compartilhados . ${\ displaystyle p (x)}$${\ displaystyle Y}$ ${\ displaystyle Y_ {i}}$${\ displaystyle P (Y_ {i} = 1 \ mid X)}$${\ displaystyle X_ {i}}$ ${\ displaystyle X}$${\ displaystyle \ beta}$

Definição do inverso da função logística

Agora podemos definir a função logit (log odds) como o inverso da função logística padrão. É fácil ver que satisfaz: ${\ displaystyle g = \ sigma ^ {- 1}}$

${\ displaystyle g (p (x)) = \ sigma ^ {- 1} (p (x)) = \ operatorname {logit} p (x) = \ ln \ left ({\ frac {p (x)} { 1-p (x)}} \ right) = \ beta _ {0} + \ beta _ {1} x,}$

e de forma equivalente, após exponenciar ambos os lados, temos as chances:

${\ displaystyle {\ frac {p (x)} {1-p (x)}} = e ^ {\ beta _ {0} + \ beta _ {1} x}.}$

Interpretação destes termos

Nas equações acima, os termos são os seguintes:

• ${\ displaystyle g}$é a função logit. A equação para ilustra que o logit (isto é, log-odds ou logaritmo natural das odds) é equivalente à expressão de regressão linear.${\ displaystyle g (p (x))}$
• ${\ displaystyle \ ln}$denota o logaritmo natural .
• ${\ displaystyle p (x)}$é a probabilidade de que a variável dependente seja igual a um caso, dada alguma combinação linear dos preditores. A fórmula para ilustra que a probabilidade da variável dependente se igualar a um caso é igual ao valor da função logística da expressão de regressão linear. Isso é importante porque mostra que o valor da expressão de regressão linear pode variar de infinito negativo a positivo e, ainda, após a transformação, a expressão resultante para a probabilidade varia entre 0 e 1.${\ displaystyle p (x)}$${\ displaystyle p (x)}$
• ${\ displaystyle \ beta _ {0}}$é a interceptação da equação de regressão linear (o valor do critério quando o preditor é igual a zero).
• ${\ displaystyle \ beta _ {1} x}$ é o coeficiente de regressão multiplicado por algum valor do preditor.
• base denota a função exponencial.${\ displaystyle e}$

Definição das probabilidades

A probabilidade da variável dependente igualar um caso (dada alguma combinação linear dos preditores) é equivalente à função exponencial da expressão de regressão linear. Isso ilustra como o logit serve como uma função de ligação entre a probabilidade e a expressão de regressão linear. Dado que o logit varia entre infinito negativo e positivo, ele fornece um critério adequado para conduzir a regressão linear e o logit é facilmente convertido de volta nas probabilidades. ${\ displaystyle x}$

Portanto, definimos as probabilidades da variável dependente igualar um caso (dada alguma combinação linear dos preditores) da seguinte forma: ${\ displaystyle x}$

${\ displaystyle {\ text {odds}} = e ^ {\ beta _ {0} + \ beta _ {1} x}.}$

O odds ratio

Para uma variável independente contínua, o odds ratio pode ser definido como:

${\ displaystyle \ mathrm {OR} = {\ frac {\ operatorname {odds} (x + 1)} {\ operatorname {odds} (x)}} = {\ frac {\ left ({\ frac {p (x +1)} {1-p (x + 1)}} \ right)} {\ left ({\ frac {p (x)} {1-p (x)}} \ right)}} = {\ frac {e ^ {\ beta _ {0} + \ beta _ {1} (x + 1)}} {e ^ {\ beta _ {0} + \ beta _ {1} x}}} = e ^ {\ beta _ {1}}}$

Essa relação exponencial fornece uma interpretação para : As probabilidades se multiplicam por para cada aumento de 1 unidade em x. ${\ displaystyle \ beta _ {1}}$${\ displaystyle e ^ {\ beta _ {1}}}$

Para uma variável binária independente, o odds ratio é definido como onde a , b , c e d são células em uma tabela de contingência 2 × 2 . ${\ displaystyle {\ frac {ad} {bc}}}$

Variáveis ​​explicativas múltiplas

Se houver várias variáveis ​​explicativas, a expressão acima pode ser revisada para . Então, quando isso é usado na equação que relaciona as chances de log de sucesso aos valores dos preditores, a regressão linear será uma regressão múltipla com m explicadores; os parâmetros para todos os j = 0, 1, 2, ..., m são todos estimados. ${\ displaystyle \ beta _ {0} + \ beta _ {1} x}$${\ displaystyle \ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2} + \ cdots + \ beta _ {m} x_ {m} = \ beta _ { 0} + \ sum _ {i = 1} ^ {m} \ beta _ {i} x_ {i}}$${\ displaystyle \ beta _ {j}}$

Novamente, as equações mais tradicionais são:

${\ displaystyle \ log {\ frac {p} {1-p}} = \ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2} + \ cdots + \ beta _ {m} x_ {m}}$

e

${\ displaystyle p = {\ frac {1} {1 + b ^ {- (\ beta _ {0} + \ beta _ {1} x_ {1} + \ beta _ {2} x_ {2} + \ cdots + \ beta _ {m} x_ {m})}}}}$

onde normalmente . ${\ displaystyle b = e}$

Adaptação do modelo

A regressão logística é um algoritmo de aprendizado de máquina importante . O objetivo é modelar a probabilidade de uma variável aleatória ser 0 ou 1 dados experimentais dados. ${\ displaystyle Y}$

Considere uma função de modelo linear generalizado parametrizada por , ${\ displaystyle \ theta}$

${\ displaystyle h _ {\ theta} (X) = {\ frac {1} {1 + e ^ {- \ theta ^ {T} X}}} = \ Pr (Y = 1 \ mid X; \ theta)}$

Portanto,

${\ displaystyle \ Pr (Y = 0 \ mid X; \ theta) = 1-h _ {\ theta} (X)}$

e uma vez que vemos que é dado por Calculamos agora a função de verossimilhança assumindo que todas as observações na amostra são distribuídas independentemente de Bernoulli, ${\ displaystyle Y \ in \ {0,1 \}}$${\ displaystyle \ Pr (y \ mid X; \ theta)}$${\ displaystyle \ Pr (y \ mid X; \ theta) = h _ {\ theta} (X) ^ {y} (1-h _ {\ theta} (X)) ^ {(1-y)}.}$

${\ displaystyle {\ begin {alinhados} L (\ theta \ mid y; x) & = \ Pr (Y \ mid X; \ theta) \\ & = \ prod _ {i} \ Pr (y_ {i} \ mid x_ {i}; \ theta) \\ & = \ prod _ {i} h _ {\ theta} (x_ {i}) ^ {y_ {i}} (1-h _ {\ theta} (x_ {i} )) ^ {(1-y_ {i})} \ end {alinhado}}}$

Normalmente, a probabilidade de log é maximizada,

${\ displaystyle N ^ {- 1} \ log L (\ theta \ mid y; x) = N ^ {- 1} \ sum _ {i = 1} ^ {N} \ log \ Pr (y_ {i} \ mid x_ {i}; \ theta)}$

que é maximizado usando técnicas de otimização, como gradiente descendente .

Assumindo que os pares são desenhados uniformemente a partir da distribuição subjacente, então no limite de N grande  , ${\ displaystyle (x, y)}$

${\ displaystyle {\ begin {align} & \ lim \ limits _ {N \ rightarrow + \ infty} N ^ {- 1} \ sum _ {i = 1} ^ {N} \ log \ Pr (y_ {i} \ mid x_ {i}; \ theta) = \ sum _ {x \ in {\ mathcal {X}}} \ sum _ {y \ in {\ mathcal {Y}}} \ Pr (X = x, Y = y) \ log \ Pr (Y = y \ mid X = x; \ theta) \\ [6pt] = {} & \ sum _ {x \ in {\ mathcal {X}}} \ sum _ {y \ in {\ mathcal {Y}}} \ Pr (X = x, Y = y) \ left (- \ log {\ frac {\ Pr (Y = y \ mid X = x)} {\ Pr (Y = y \ mid X = x; \ theta)}} + \ log \ Pr (Y = y \ mid X = x) \ right) \\ [6pt] = {} & - D _ {\ text {KL}} (Y \ paralelo Y _ {\ theta}) - H (Y \ mid X) \ end {alinhado}}}$

onde está a entropia condicional e é a divergência de Kullback-Leibler . Isso leva à intuição de que, ao maximizar a probabilidade logarítmica de um modelo, você está minimizando a divergência KL de seu modelo em relação à distribuição de entropia máxima. Busca intuitiva pelo modelo que faz menos suposições em seus parâmetros. ${\ displaystyle H (Y \ mid X)}$${\ displaystyle D _ {\ text {KL}}}$

"Regra dos dez"

Uma regra prática amplamente usada, a " regra um em dez ", afirma que os modelos de regressão logística fornecem valores estáveis ​​para as variáveis ​​explicativas se baseados em um mínimo de cerca de 10 eventos por variável explicativa (VPE); onde evento denota os casos pertencentes à categoria menos frequente na variável dependente. Portanto, um estudo projetado para usar variáveis ​​explicativas para um evento (por exemplo, infarto do miocárdio ) que deve ocorrer em uma proporção de participantes do estudo exigirá um total de participantes. No entanto, há um debate considerável sobre a confiabilidade dessa regra, que é baseada em estudos de simulação e carece de um suporte teórico seguro. De acordo com alguns autores, a regra é excessivamente conservadora em algumas circunstâncias, com os autores declarando: "Se nós (um tanto subjetivamente) considerarmos a cobertura do intervalo de confiança menor que 93 por cento, erro tipo I maior que 7 por cento ou viés relativo maior que 15 por cento como problemático, nossos resultados indicam que os problemas são bastante frequentes com 2–4 EPV, incomuns com 5–9 EPV e ainda observados com 10–16 EPV. Os piores casos de cada problema não foram graves com 5–9 EPV e geralmente comparáveis ​​a aqueles com 10-16 EPV ". ${\ displaystyle k}$${\ displaystyle p}$${\ displaystyle 10k / p}$

Outros encontraram resultados que não são consistentes com os anteriores, usando critérios diferentes. Um critério útil é se o modelo ajustado deverá atingir a mesma discriminação preditiva em uma nova amostra como parecia atingir na amostra de desenvolvimento do modelo. Para esse critério, podem ser necessários 20 eventos por variável candidata. Além disso, pode-se argumentar que 96 observações são necessárias apenas para estimar a interceptação do modelo com precisão suficiente para que a margem de erro nas probabilidades previstas seja de ± 0,1 com um nível de confiança de 0,95.

Estimativa de máxima verossimilhança (MLE)

Os coeficientes de regressão são geralmente estimados usando estimativa de máxima verossimilhança . Ao contrário da regressão linear com resíduos normalmente distribuídos, não é possível encontrar uma expressão de forma fechada para os valores dos coeficientes que maximizam a função de verossimilhança, de modo que um processo iterativo deve ser usado em seu lugar; por exemplo, o método de Newton . Esse processo começa com uma solução provisória, revisa-a levemente para ver se pode ser melhorada e repete essa revisão até que nenhuma outra melhoria seja feita, ponto em que o processo teria convergido.

Em alguns casos, o modelo pode não atingir a convergência. A não convergência de um modelo indica que os coeficientes não são significativos porque o processo iterativo não foi capaz de encontrar soluções adequadas. Uma falha na convergência pode ocorrer por uma série de razões: ter uma grande proporção de preditores para casos, multicolinearidade , dispersão ou separação completa .

• Ter uma grande proporção de variáveis ​​para casos resulta em uma estatística de Wald excessivamente conservadora (discutida abaixo) e pode levar à não convergência. A regressão logística regularizada destina-se especificamente a ser usada nessa situação.
• Multicolinearidade refere-se a correlações inaceitavelmente altas entre preditores. À medida que a multicolinearidade aumenta, os coeficientes permanecem imparciais, mas os erros padrão aumentam e a probabilidade de convergência do modelo diminui. Para detectar a multicolinearidade entre os preditores, pode-se realizar uma análise de regressão linear com os preditores de interesse com o único propósito de examinar a estatística de tolerância usada para avaliar se a multicolinearidade é inaceitavelmente alta.
• Disparidade nos dados refere-se a ter uma grande proporção de células vazias (células com contagem zero). A contagem de células zero é particularmente problemática com preditores categóricos. Com preditores contínuos, o modelo pode inferir valores para as contagens de células zero, mas esse não é o caso com preditores categóricos. O modelo não convergirá com contagens de células zero para preditores categóricos porque o logaritmo natural de zero é um valor indefinido para que a solução final para o modelo não possa ser alcançada. Para remediar esse problema, os pesquisadores podem reduzir as categorias de uma forma teoricamente significativa ou adicionar uma constante a todas as células.
• Outro problema numérico que pode levar à falta de convergência é a separação completa, que se refere à instância em que os preditores predizem perfeitamente o critério - todos os casos são classificados com precisão. Nesses casos, deve-se reexaminar os dados, pois é provável que haja algum tipo de erro.
• Pode-se também adotar abordagens semiparamétricas ou não paramétricas, por exemplo, por meio de métodos de verossimilhança local ou não paramétricos, que evitam suposições de uma forma paramétrica para a função de índice e são robustas para a escolha da função de ligação (por exemplo, probit ou logit).

Função de perda de entropia cruzada

Em aplicativos de aprendizado de máquina onde a regressão logística é usada para classificação binária, o MLE minimiza a função de perda de entropia cruzada .

Mínimos quadrados reponderados iterativamente (IRLS)

A regressão logística binária ( ou ) pode, por exemplo, ser calculada usando mínimos quadrados reponderados iterativamente (IRLS), o que é equivalente a maximizar a probabilidade log de um processo distribuído de Bernoulli usando o método de Newton . Se o problema for escrito na forma de matriz vetorial, com parâmetros , variáveis ​​explicativas e valor esperado da distribuição de Bernoulli , os parâmetros podem ser encontrados usando o seguinte algoritmo iterativo: ${\ displaystyle y = 0}$${\ displaystyle y = 1}$${\ displaystyle \ mathbf {w} ^ {T} = [\ beta _ {0}, \ beta _ {1}, \ beta _ {2}, \ ldots]}$${\ displaystyle \ mathbf {x} (i) = [1, x_ {1} (i), x_ {2} (i), \ ldots] ^ {T}}$${\ displaystyle \ mu (i) = {\ frac {1} {1 + e ^ {- \ mathbf {w} ^ {T} \ mathbf {x} (i)}}}}$${\ displaystyle \ mathbf {w}}$

${\ displaystyle \ mathbf {w} _ {k + 1} = \ left (\ mathbf {X} ^ {T} \ mathbf {S} _ {k} \ mathbf {X} \ right) ^ {- 1} \ mathbf {X} ^ {T} \ left (\ mathbf {S} _ {k} \ mathbf {X} \ mathbf {w} _ {k} + \ mathbf {y} - \ mathbf {\ boldsymbol {\ mu} } _ {k} \ right)}$

onde é uma matriz de ponderação diagonal, o vetor de valores esperados, ${\ displaystyle \ mathbf {S} = \ operatorname {diag} (\ mu (i) (1- \ mu (i)))}$${\ displaystyle {\ boldsymbol {\ mu}} = [\ mu (1), \ mu (2), \ ldots]}$

${\ displaystyle \ mathbf {X} = {\ begin {bmatrix} 1 & x_ {1} (1) & x_ {2} (1) & \ ldots \\ 1 & x_ {1} (2) & x_ {2} (2) & \ ldots \\\ vdots & \ vdots & \ vdots \ end {bmatrix}}}$

A matriz de regressor e o vetor de variáveis ​​de resposta. Mais detalhes podem ser encontrados na literatura. ${\ displaystyle \ mathbf {y} (i) = [y (1), y (2), \ ldots] ^ {T}}$

Avaliação da qualidade do ajuste

A qualidade do ajuste em modelos de regressão linear é geralmente medida usando R ² . Como não há analogia direta na regressão logística, vários métodos, incluindo o seguinte, podem ser usados.

Testes de desvio e razão de verossimilhança

Na análise de regressão linear, preocupa-se com o particionamento da variância por meio dos cálculos da soma dos quadrados - a variância no critério é essencialmente dividida em variância contabilizada pelos preditores e variância residual. Na análise de regressão logística, o desvio é usado no lugar de cálculos de soma de quadrados. O desvio é análogo à soma dos cálculos dos quadrados na regressão linear e é uma medida da falta de ajuste aos dados em um modelo de regressão logística. Quando um modelo "saturado" está disponível (um modelo com um ajuste teoricamente perfeito), o desvio é calculado comparando um determinado modelo com o modelo saturado. Este cálculo fornece o teste de razão de verossimilhança :

${\ displaystyle D = -2 \ ln {\ frac {\ text {probabilidade do modelo ajustado}} {\ text {probabilidade do modelo saturado}}}.}$

Na equação acima, D representa o desvio e ln representa o logaritmo natural. O log dessa razão de verossimilhança (a razão do modelo ajustado para o modelo saturado) produzirá um valor negativo, daí a necessidade de um sinal negativo. D pode ser mostrado para seguir uma distribuição qui-quadrada aproximada . Valores menores indicam melhor ajuste, pois o modelo ajustado se desvia menos do modelo saturado. Quando avaliados em uma distribuição qui-quadrado, valores não significativos de qui-quadrado indicam muito pouca variância inexplicada e, portanto, um bom ajuste do modelo. Por outro lado, um valor significativo de qui-quadrado indica que uma quantidade significativa da variação não é explicada.

Quando o modelo saturado não está disponível (um caso comum), o desvio é calculado simplesmente como −2 · (probabilidade log do modelo ajustado), e a referência à probabilidade log do modelo saturado pode ser removida de tudo o que segue sem danos.

Duas medidas de desvio são particularmente importantes na regressão logística: desvio nulo e desvio do modelo. O desvio nulo representa a diferença entre um modelo com apenas a interceptação (o que significa "sem preditores") e o modelo saturado. O desvio do modelo representa a diferença entre um modelo com pelo menos um preditor e o modelo saturado. A este respeito, o modelo nulo fornece uma linha de base sobre a qual comparar os modelos preditores. Dado que o desvio é uma medida da diferença entre um determinado modelo e o modelo saturado, valores menores indicam melhor ajuste. Assim, para avaliar a contribuição de um preditor ou conjunto de preditores, pode-se subtrair o desvio do modelo do desvio nulo e avaliar a diferença em uma distribuição qui-quadrado com graus de liberdade iguais à diferença no número de parâmetros estimados. ${\ displaystyle \ chi _ {sp} ^ {2},}$

Deixar

${\ displaystyle {\ begin {alinhados} D _ {\ text {null}} & = - 2 \ ln {\ frac {\ text {probabilidade do modelo nulo}} {\ text {probabilidade do modelo saturado}}} \\ [6pt] D _ {\ text {apropriado}} & = - 2 \ ln {\ frac {\ text {probabilidade do modelo ajustado}} {\ text {probabilidade do modelo saturado}}}. \ End {alinhado}}}$

Então, a diferença de ambos é:

${\ displaystyle {\ begin {alinhados} D _ {\ text {null}} - D _ {\ text {apropriado}} & = - 2 \ left (\ ln {\ frac {\ text {probabilidade de modelo nulo}} {\ text {probabilidade do modelo saturado}}} - \ ln {\ frac {\ text {probabilidade do modelo ajustado}} {\ text {probabilidade do modelo saturado}}} \ right) \\ [6pt] & = - 2 \ ln {\ frac {\ left ({\ dfrac {\ text {probabilidade do modelo nulo}} {\ text {probabilidade do modelo saturado}}} \ right)} {\ left ({\ dfrac {\ text {probabilidade do modelo ajustado}} {\ text {probabilidade do modelo saturado}}} \ right)}} \\ [6pt] & = - 2 \ ln {\ frac {\ text {probabilidade do modelo nulo}} {\ text {probabilidade do modelo ajustado}}}. \ end {alinhado}}}$

Se o desvio do modelo for significativamente menor do que o desvio nulo, pode-se concluir que o preditor ou conjunto de preditores melhora significativamente o ajuste do modelo. Isso é análogo ao teste F usado na análise de regressão linear para avaliar a significância da previsão.

Pseudo-R-quadrado

Na regressão linear, a correlação múltipla quadrada, R² é usado para avaliar a qualidade do ajuste, pois representa a proporção da variância no critério que é explicada pelos preditores. Na análise de regressão logística, não há uma medida análoga acordada, mas existem várias medidas concorrentes, cada uma com limitações.

Quatro dos índices mais comumente usados ​​e um menos comumente usado são examinados nesta página:

• Razão de verossimilhança R ² _L
• Cox e Snell R ² _CS
• Nagelkerke R ² _N
• McFadden R ² _MCF
• Tjur R ² _t

R ² _L é dado por Cohen:

${\ displaystyle R _ {\ text {L}} ^ {2} = {\ frac {D _ {\ text {null}} - D _ {\ text {apropriado}}} {D _ {\ text {null}}}}. }$

Este é o índice mais análogo às correlações múltiplas ao quadrado na regressão linear. Representa a redução proporcional no desvio em que o desvio é tratado como uma medida de variação análoga, mas não idêntica à variância na análise de regressão linear . Uma limitação da razão de verossimilhança R² é que ela não está monotonicamente relacionada à razão de chance, o que significa que não necessariamente aumenta à medida que a razão de chance aumenta e não necessariamente diminui à medida que a razão de chance diminui.

R ² _CS é um índice alternativo de qualidade de ajuste relacionada com o R valor ² de regressão linear. É dado por:

${\ displaystyle {\ begin {alinhados} R _ {\ text {CS}} ^ {2} & = 1- \ left ({\ frac {L_ {0}} {L_ {M}}} \ right) ^ {2 / n} \\ [5pt] & = 1-e ^ {2 (\ ln (L_ {0}) - \ ln (L_ {M})) / n} \ end {alinhado}}}$

onde L _M e L ₀ são as probabilidades do modelo sendo ajustado e do modelo nulo, respectivamente. O índice de Cox e Snell é problemático, pois seu valor máximo é . O máximo que esse limite superior pode ser é 0,75, mas pode facilmente ser tão baixo quanto 0,48 quando a proporção marginal de casos é pequena. ${\ displaystyle 1-L_ {0} ^ {2 / n}}$

R ² _N fornece uma correcção para a Cox e Snell R ² de modo a que o valor máximo é igual a 1. No entanto, os Cox e Snell e razão de probabilidade de P ²s mostrar maior acordo uns com os outros do que quer faz com o Nagelkerke R m². Obviamente, esse pode não ser o caso para valores que excedem 0,75, pois o índice de Cox e Snell é limitado a esse valor. A taxa de probabilidade R 'é muitas vezes preferido para as alternativas, uma vez que é mais análogo a R ² em regressão linear , é independente da taxa de base (tanto Cox e Snell e Nagelkerke R aumento ²s como a proporção dos casos aumentar 0-0,5) e varia entre 0 e 1.

R ² _McF é definido como

${\ displaystyle R _ {\ text {McF}} ^ {2} = 1 - {\ frac {\ ln (L_ {M})} {\ ln (L_ {0})}},}$

e é preferido em relação R ² _CS por Allison. As duas expressões R ² _McF e R ² _CS são então relacionadas respectivamente por,

${\ displaystyle {\ begin {matrix} R _ {\ text {CS}} ^ {2} = 1- \ left ({\ dfrac {1} {L_ {0}}} \ right) ^ {\ frac {2 ( R _ {\ text {McF}} ^ {2})} {n}} \\ [1.5em] R _ {\ text {McF}} ^ {2} = - {\ dfrac {n} {2}} \ cdot {\ dfrac {\ ln (1-R _ {\ text {CS}} ^ {2})} {\ ln L_ {0}}} \ end {matriz}}}$

No entanto, Allison agora prefere R ² _T que é uma medida relativamente nova desenvolvida pela tjur. Pode ser calculado em duas etapas:

1. Para cada nível da variável dependente, encontre a média das probabilidades previstas de um evento.
2. Pegue o valor absoluto da diferença entre essas médias

Uma palavra de cautela é necessária ao interpretar as estatísticas pseudo- R² . A razão pela qual esses índices de ajuste são chamados de pseudo R² é que eles não representam a redução proporcional no erro como o R² na regressão linear representa . A regressão linear assume homocedasticidade , que a variância do erro é a mesma para todos os valores do critério. A regressão logística sempre será heterocedástica - as variâncias do erro diferem para cada valor da pontuação prevista. Para cada valor da pontuação prevista, haveria um valor diferente da redução proporcional do erro. Portanto, é inapropriado pensar em R² como uma redução proporcional do erro em um sentido universal na regressão logística.

Teste Hosmer-Lemeshow

O teste Hosmer-Lemeshow usa uma estatística de teste que segue assintoticamente uma distribuição para avaliar se as taxas de eventos observadas correspondem ou não às taxas de eventos esperadas em subgrupos da população do modelo. Este teste é considerado obsoleto por alguns estatísticos por causa de sua dependência de binning arbitrário de probabilidades preditas e baixo poder relativo. ${\ displaystyle \ chi ^ {2}}$

Coeficientes

Depois de ajustar o modelo, é provável que os pesquisadores queiram examinar a contribuição de preditores individuais. Para fazer isso, eles vão querer examinar os coeficientes de regressão. Na regressão linear, os coeficientes de regressão representam a mudança no critério para cada mudança de unidade no preditor. Na regressão logística, no entanto, os coeficientes de regressão representam a mudança no logit para cada mudança de unidade no preditor. Dado que o logit não é intuitivo, os pesquisadores provavelmente se concentrarão no efeito de um preditor sobre a função exponencial do coeficiente de regressão - a razão de chances (ver definição ). Na regressão linear, a significância de um coeficiente de regressão é avaliada pelo cálculo de um teste t . Na regressão logística, existem vários testes diferentes projetados para avaliar a significância de um preditor individual, mais notavelmente o teste da razão de verossimilhança e a estatística de Wald.

Teste de razão de verossimilhança

O teste de razão de verossimilhança discutido acima para avaliar o ajuste do modelo também é o procedimento recomendado para avaliar a contribuição de "preditores" individuais para um determinado modelo. No caso de um único modelo preditor, basta comparar o desvio do modelo preditor com o do modelo nulo em uma distribuição qui-quadrado com um único grau de liberdade. Se o modelo preditor tem desvio significativamente menor (cf qui-quadrado usando a diferença em graus de liberdade dos dois modelos), pode-se concluir que há uma associação significativa entre o "preditor" e o resultado. Embora alguns pacotes estatísticos comuns (por exemplo, SPSS) forneçam estatísticas de teste de razão de verossimilhança, sem esse teste computacionalmente intensivo seria mais difícil avaliar a contribuição de preditores individuais no caso de regressão logística múltipla. Para avaliar a contribuição de preditores individuais, pode-se inserir os preditores hierarquicamente, comparando cada novo modelo com o anterior para determinar a contribuição de cada preditor. Há algum debate entre os estatísticos sobre a adequação dos chamados procedimentos "graduais". O temor é que eles não preservem propriedades estatísticas nominais e possam se tornar enganosos.

Estatística de Wald

Alternativamente, ao avaliar a contribuição de preditores individuais em um determinado modelo, pode-se examinar a significância da estatística de Wald . A estatística de Wald, análoga ao teste t na regressão linear, é usada para avaliar a significância dos coeficientes. A estatística Wald é a razão entre o quadrado do coeficiente de regressão e o quadrado do erro padrão do coeficiente e é distribuída assintoticamente como uma distribuição qui-quadrado.

${\ displaystyle W_ {j} = {\ frac {\ beta _ {j} ^ {2}} {SE _ {\ beta _ {j}} ^ {2}}}}$

Embora vários pacotes estatísticos (por exemplo, SPSS, SAS) relatem a estatística de Wald para avaliar a contribuição de preditores individuais, a estatística de Wald tem limitações. Quando o coeficiente de regressão é grande, o erro padrão do coeficiente de regressão também tende a ser maior, aumentando a probabilidade de erro Tipo II . A estatística de Wald também tende a ser tendenciosa quando os dados são esparsos.

Amostragem caso-controle

Suponha que os casos sejam raros. Então, podemos desejar amostrá-los com mais frequência do que sua prevalência na população. Por exemplo, suponha que haja uma doença que afete 1 pessoa em 10.000 e, para coletar nossos dados, precisamos fazer um exame físico completo. Pode ser muito caro fazer milhares de exames físicos de pessoas saudáveis ​​para obter dados de apenas alguns indivíduos doentes. Assim, podemos avaliar mais indivíduos doentes, talvez todos os resultados raros. Esta também é uma amostragem retrospectiva ou, de forma equivalente, é chamada de dados não balanceados. Como regra geral, os controles de amostragem a uma taxa de cinco vezes o número de casos produzirão dados de controle suficientes.

A regressão logística é única no sentido de que pode ser estimada em dados não balanceados, em vez de dados amostrados aleatoriamente, e ainda produz estimativas de coeficiente corretas dos efeitos de cada variável independente no resultado. Ou seja, se formarmos um modelo logístico a partir desses dados, se o modelo estiver correto na população em geral, os parâmetros estarão todos corretos, exceto . Podemos corrigir se conhecermos a verdadeira prevalência da seguinte forma: ${\ displaystyle \ beta _ {j}}$${\ displaystyle \ beta _ {0}}$${\ displaystyle \ beta _ {0}}$

${\ displaystyle {\ widehat {\ beta}} _ {0} ^ {*} = {\ widehat {\ beta}} _ {0} + \ log {\ frac {\ pi} {1- \ pi}} - \ log {{\ tilde {\ pi}} \ over {1 - {\ tilde {\ pi}}}}}$

onde é a verdadeira prevalência e é a prevalência na amostra. ${\ displaystyle \ pi}$${\ displaystyle {\ tilde {\ pi}}}$

Especificação matemática formal

Existem várias especificações equivalentes de regressão logística, que se encaixam em diferentes tipos de modelos mais gerais. Essas especificações diferentes permitem diferentes tipos de generalizações úteis.

Configurar

A configuração básica da regressão logística é a seguinte. Recebemos um conjunto de dados contendo N pontos. Cada ponto i consiste em um conjunto de m variáveis ​​de entrada x _{1, i} ... x _{m, i} (também chamadas de variáveis ​​independentes , variáveis ​​preditoras, recursos ou atributos) e uma variável de resultado binária Y _i (também conhecida como dependente variável , variável de resposta, variável de saída ou classe), ou seja, pode assumir apenas os dois valores possíveis 0 (frequentemente significando "não" ou "falha") ou 1 (frequentemente significando "sim" ou "sucesso"). O objetivo da regressão logística é usar o conjunto de dados para criar um modelo preditivo da variável de resultado.

Como na regressão linear, presume-se que as variáveis ​​de resultado Y _i dependem das variáveis ​​explicativas x _{1, i} ... x _{m, i} .

Variáveis ​​explicativas

As variáveis ​​explicativas podem ser de qualquer tipo : com valor real , binárias , categóricas , etc. A principal distinção é entre variáveis ​​contínuas e variáveis ​​discretas .

(Variáveis ​​discretas referindo-se a mais de duas escolhas possíveis são normalmente codificadas usando variáveis ​​dummy (ou variáveis ​​indicadoras ), isto é, variáveis ​​explicativas separadas tomando o valor 0 ou 1 são criadas para cada valor possível da variável discreta, com um significado 1 " a variável tem o valor fornecido "e um 0 significa" a variável não tem esse valor ".)

Variáveis ​​de resultado

Formalmente, os resultados Y _i são descritos como dados distribuídos de Bernoulli , onde cada resultado é determinado por uma probabilidade não observada p _i que é específica para o resultado em questão, mas relacionada às variáveis ​​explicativas. Isso pode ser expresso em qualquer uma das seguintes formas equivalentes:

${\ displaystyle {\ begin {alinhado} Y_ {i} \ mid x_ {1, i}, \ ldots, x_ {m, i} \ & \ sim \ operatorname {Bernoulli} (p_ {i}) \\\ operatorname {\ mathcal {E}} [Y_ {i} \ mid x_ {1, i}, \ ldots, x_ {m, i}] & = p_ {i} \\\ Pr (Y_ {i} = y \ mid x_ {1, i}, \ ldots, x_ {m, i}) & = {\ begin {cases} p_ {i} & {\ text {if}} y = 1 \\ 1-p_ {i} & { \ text {if}} y = 0 \ end {cases}} \\\ Pr (Y_ {i} = y \ mid x_ {1, i}, \ ldots, x_ {m, i}) & = p_ {i } ^ {y} (1-p_ {i}) ^ {(1-y)} \ end {alinhado}}}$

Os significados dessas quatro linhas são:

1. A primeira linha expressa a distribuição de probabilidade de cada Y _i : condicionada às variáveis ​​explicativas, segue uma distribuição de Bernoulli com os parâmetros p _i , a probabilidade do resultado de 1 para a tentativa i . Conforme observado acima, cada tentativa separada tem sua própria probabilidade de sucesso, assim como cada tentativa tem suas próprias variáveis ​​explicativas. A probabilidade de sucesso p _i não é observada, apenas o resultado de uma tentativa individual de Bernoulli usando essa probabilidade.
2. A segunda linha expressa o fato de que o valor esperado de cada Y _i é igual à probabilidade de sucesso p _i , que é uma propriedade geral da distribuição de Bernoulli. Em outras palavras, se executarmos um grande número de tentativas de Bernoulli usando a mesma probabilidade de sucesso p _i , então tirarmos a média de todos os resultados 1 e 0, então o resultado seria próximo de p _i . Isso ocorre porque fazer uma média dessa maneira simplesmente calcula a proporção de sucessos vistos, que esperamos convergir para a probabilidade de sucesso subjacente.
3. A terceira linha escreve a função de massa de probabilidade da distribuição de Bernoulli, especificando a probabilidade de ver cada um dos dois resultados possíveis.
4. A quarta linha é outra maneira de escrever a função de massa de probabilidade, o que evita ter que escrever casos separados e é mais conveniente para certos tipos de cálculos. Isso se baseia no fato de que Y _i pode assumir apenas o valor 0 ou 1. Em cada caso, um dos expoentes será 1, "escolhendo" o valor abaixo dele, enquanto o outro é 0, "cancelando" o valor abaixo isto. Portanto, o resultado é p _i ou 1 -  p _i , como na linha anterior.

Função de predição linear

A ideia básica da regressão logística é usar o mecanismo já desenvolvido para a regressão linear modelando a probabilidade p _i usando uma função de predição linear , ou seja, uma combinação linear das variáveis ​​explicativas e um conjunto de coeficientes de regressão que são específicos para o modelo em questão mas o mesmo para todas as tentativas. A função de preditor linear para um determinado ponto de dados i é escrita como: ${\ displaystyle f (i)}$

${\ displaystyle f (i) = \ beta _ {0} + \ beta _ {1} x_ {1, i} + \ cdots + \ beta _ {m} x_ {m, i},}$

onde estão os coeficientes de regressão que indicam o efeito relativo de uma determinada variável explicativa no resultado. ${\ displaystyle \ beta _ {0}, \ ldots, \ beta _ {m}}$

O modelo é geralmente colocado em uma forma mais compacta da seguinte forma:

• Os coeficientes de regressão β ₀ , β ₁ , ..., β _m são agrupados em um único vetor β de tamanho m  + 1.
• Para cada ponto de dados i , uma pseudo-variável explicativa adicional x _{0, i} é adicionada, com um valor fixo de 1, correspondendo ao coeficiente de interceptação β ₀ .
• As variáveis ​​explicativas resultantes x _{0, i} , x _{1, i} , ..., x _{m, i} são então agrupadas em um único vetor X _i de tamanho m  + 1.

Isso torna possível escrever a função de preditor linear da seguinte forma:

${\ displaystyle f (i) = {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i},}$

usando a notação para um produto escalar entre dois vetores.

Como um modelo linear generalizado

O modelo específico usado pela regressão logística, que o distingue da regressão linear padrão e de outros tipos de análise de regressão usados ​​para resultados de valor binário , é a maneira como a probabilidade de um resultado específico está ligada à função de preditor linear:

${\ displaystyle \ operatorname {logit} (\ operatorname {\ mathcal {E}} [Y_ {i} \ mid x_ {1, i}, \ ldots, x_ {m, i}]) = \ operatorname {logit} ( p_ {i}) = \ ln \ left ({\ frac {p_ {i}} {1-p_ {i}}} \ right) = \ beta _ {0} + \ beta _ {1} x_ {1, i} + \ cdots + \ beta _ {m} x_ {m, i}}$

Escrito usando a notação mais compacta descrita acima, é:

${\ displaystyle \ operatorname {logit} (\ operatorname {\ mathcal {E}} [Y_ {i} \ mid \ mathbf {X} _ {i}]) = \ operatorname {logit} (p_ {i}) = \ ln \ left ({\ frac {p_ {i}} {1-p_ {i}}} \ right) = {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}}$

Esta formulação expressa a regressão logística como um tipo de modelo linear generalizado , que prevê variáveis ​​com vários tipos de distribuições de probabilidade ajustando uma função preditora linear da forma acima a algum tipo de transformação arbitrária do valor esperado da variável.

A intuição para transformar usando a função logit (o log natural das probabilidades) foi explicada acima. Ele também tem o efeito prático de converter a probabilidade (que é limitada a estar entre 0 e 1) em uma variável que varia além - correspondendo, assim, ao intervalo de potencial da função de predição linear no lado direito da equação. ${\ displaystyle (- \ infty, + \ infty)}$

Note-se que tanto a probabilidade p _i e os coeficientes de regressão não são observadas, e os meios de determinar-lhes que não faz parte do próprio modelo. Eles são normalmente determinados por algum tipo de procedimento de otimização, por exemplo, estimativa de máxima verossimilhança , que encontra os valores que melhor se ajustam aos dados observados (ou seja, que fornecem as previsões mais precisas para os dados já observados), geralmente sujeitos a condições de regularização que procuram excluir o improvável valores, por exemplo, valores extremamente grandes para qualquer um dos coeficientes de regressão. O uso de uma condição de regularização é equivalente a fazer estimativa do máximo a posteriori (MAP), uma extensão da máxima verossimilhança. (A regularização é mais comumente feita usando uma função de regularização quadrada , que é equivalente a colocar uma distribuição anterior gaussiana de média zero nos coeficientes, mas outros regularizadores também são possíveis.) Quer a regularização seja usada ou não, geralmente não é possível encontrar uma solução de forma fechada; em vez disso, um método numérico iterativo deve ser usado, como mínimos quadrados reponderados iterativamente (IRLS) ou, mais comumente hoje em dia, um método quase Newton como o método L-BFGS .

A interpretação das estimativas do parâmetro β _j é como o efeito aditivo no log das chances de uma mudança unitária na variável explicativa j . No caso de uma variável explicativa dicotômica, por exemplo, gênero é a estimativa das chances de ter o resultado para, digamos, homens em comparação com mulheres. ${\ displaystyle e ^ {\ beta}}$

Uma fórmula equivalente usa o inverso da função logit, que é a função logística , ou seja:

${\ displaystyle \ operatorname {\ mathcal {E}} [Y_ {i} \ mid \ mathbf {X} _ {i}] = p_ {i} = \ operatorname {logit} ^ {- 1} ({\ boldsymbol { \ beta}} \ cdot \ mathbf {X} _ {i}) = {\ frac {1} {1 + e ^ {- {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}} }}}$

A fórmula também pode ser escrita como uma distribuição de probabilidade (especificamente, usando uma função de massa de probabilidade ):

${\ displaystyle \ Pr (Y_ {i} = y \ mid \ mathbf {X} _ {i}) = {p_ {i}} ^ {y} (1-p_ {i}) ^ {1-y} = \ left ({\ frac {e ^ {{\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}}} {1 + e ^ {{\ boldsymbol {\ beta}} \ cdot \ mathbf { X} _ {i}}}} \ right) ^ {y} \ left (1 - {\ frac {e ^ {{\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}}} { 1 + e ^ {{\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}}}} \ right) ^ {1-y} = {\ frac {e ^ {{\ boldsymbol {\ beta }} \ cdot \ mathbf {X} _ {i} \ cdot y}} {1 + e ^ {{\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}}}}}$

Como um modelo de variável latente

O modelo acima tem uma formulação equivalente como modelo de variável latente . Essa formulação é comum na teoria dos modelos de escolha discreta e torna mais fácil estender a certos modelos mais complicados com escolhas múltiplas correlacionadas, bem como comparar a regressão logística ao modelo probit intimamente relacionado .

Imagine que, para cada tentativa i , existe uma variável latente contínua Y _i ^* (ou seja, uma variável aleatória não observada ) que é distribuída da seguinte forma:

${\ displaystyle Y_ {i} ^ {\ ast} = {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i} + \ varepsilon \,}$

Onde

${\ displaystyle \ varepsilon \ sim \ operatorname {Logística} (0,1) \,}$

ou seja, a variável latente pode ser escrita diretamente em termos da função de predição linear e uma variável de erro aleatório aditiva que é distribuída de acordo com uma distribuição logística padrão .

Então Y _i pode ser visto como um indicador para saber se esta variável latente é positiva:

${\ displaystyle Y_ {i} = {\ begin {cases} 1 & {\ text {if}} Y_ {i} ^ {\ ast}> 0 \ {\ text {ie}} - \ varejpsilon <{\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}, \\ 0 & {\ text {caso contrário.}} \ end {cases}}}$

A escolha de modelar a variável de erro especificamente com uma distribuição logística padrão, em vez de uma distribuição logística geral com a localização e a escala definidas para valores arbitrários, parece restritiva, mas na verdade, não é. Deve-se ter em mente que podemos escolher nós mesmos os coeficientes de regressão e, muitas vezes, podemos usá-los para compensar as mudanças nos parâmetros da distribuição da variável de erro. Por exemplo, uma distribuição de variável de erro logístico com um parâmetro de localização diferente de zero μ (que define a média) é equivalente a uma distribuição com um parâmetro de localização zero, onde μ foi adicionado ao coeficiente de interceptação. Ambas as situações produzem o mesmo valor para Y _i ^*, independentemente das configurações das variáveis ​​explicativas. Da mesma forma, um parâmetro de escala arbitrário s é equivalente a definir o parâmetro de escala para 1 e então dividir todos os coeficientes de regressão por s . No último caso, o valor resultante de Y _i ^* será menor por um fator de s do que no primeiro caso, para todos os conjuntos de variáveis ​​explicativas - mas, criticamente, ele sempre permanecerá do mesmo lado de 0 e, portanto, conduzirá para a mesma escolha Y _i .

(Observe que isso prevê que a irrelevância do parâmetro de escala pode não ser transportada para modelos mais complexos, onde mais de duas opções estão disponíveis.)

Acontece que esta formulação é exatamente equivalente à anterior, formulada em termos do modelo linear generalizado e sem quaisquer variáveis ​​latentes . Isso pode ser mostrado da seguinte forma, usando o fato de que a função de distribuição cumulativa (CDF) da distribuição logística padrão é a função logística , que é o inverso da função logit , ou seja,

${\ displaystyle \ Pr (\ varepsilon <x) = \ operatorname {logit} ^ {- 1} (x)}$

Então:

${\ displaystyle {\ begin {alinhados} \ Pr (Y_ {i} = 1 \ mid \ mathbf {X} _ {i}) & = \ Pr (Y_ {i} ^ {\ ast}> 0 \ mid \ mathbf {X} _ {i}) \\ [5pt] & = \ Pr ({\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i} + \ varepsilon> 0) \\ [5pt] & = \ Pr (\ varepsilon> - {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}) \\ [5pt] & = \ Pr (\ varepsilon <{\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}) && {\ text {(porque a distribuição logística é simétrica)}} \\ [5pt] & = \ operatorname {logit} ^ {- 1} ({\ boldsymbol {\ beta} } \ cdot \ mathbf {X} _ {i}) & \\ [5pt] & = p_ {i} && {\ text {(veja acima)}} \ end {alinhado}}}$

Esta formulação - que é padrão em modelos de escolha discreta - deixa clara a relação entre a regressão logística (o "modelo logit") e o modelo probit , que usa uma variável de erro distribuída de acordo com uma distribuição normal padrão em vez de uma distribuição logística padrão. Ambas as distribuições, logística e normal, são simétricas com uma forma básica unimodal de "curva em sino". A única diferença é que a distribuição logística tem caudas um pouco mais pesadas , o que significa que é menos sensível a dados remotos (e, portanto, um pouco mais robusta para modelar especificações incorretas ou dados errôneos).

Modelo de variável latente bidirecional

Ainda outra formulação usa duas variáveis ​​latentes separadas:

${\ displaystyle {\ begin {alinhados} Y_ {i} ^ {0 \ ast} & = {\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i} + \ varejpsilon _ {0 } \, \\ Y_ {i} ^ {1 \ ast} & = {\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i} + \ varepsilon _ {1} \, \ fim {alinhado}}}$

Onde

${\ displaystyle {\ begin {alinhados} \ varepsilon _ {0} & \ sim \ operatorname {EV} _ {1} (0,1) \\\ varejpsilon _ {1} & \ sim \ operatorname {EV} _ { 1} (0,1) \ end {alinhado}}}$

onde EV ₁ (0,1) é uma distribuição de valor extremo tipo 1 padrão : ie

${\ displaystyle \ Pr (\ varepsilon _ {0} = x) = \ Pr (\ varepsilon _ {1} = x) = e ^ {- x} e ^ {- e ^ {- x}}}$

Então

${\ displaystyle Y_ {i} = {\ begin {cases} 1 & {\ text {if}} Y_ {i} ^ {1 \ ast}> Y_ {i} ^ {0 \ ast}, \\ 0 & {\ text {caso contrário.}} \ end {cases}}}$

Este modelo possui uma variável latente separada e um conjunto separado de coeficientes de regressão para cada resultado possível da variável dependente. O motivo dessa separação é que ela torna mais fácil estender a regressão logística para variáveis ​​categóricas de múltiplos resultados, como no modelo logit multinomial . Nesse modelo, é natural modelar cada resultado possível usando um conjunto diferente de coeficientes de regressão. Também é possível motivar cada uma das variáveis ​​latentes separadas como a utilidade teórica associada a fazer a escolha associada e, assim, motivar a regressão logística em termos de teoria da utilidade . (Em termos de teoria da utilidade, um ator racional sempre escolhe a escolha com a maior utilidade associada.) Esta é a abordagem adotada pelos economistas ao formular modelos de escolha discreta , porque fornece uma base teoricamente forte e facilita intuições sobre o modelo, o que por sua vez, torna mais fácil considerar vários tipos de extensões. (Veja o exemplo abaixo.)

A escolha da distribuição de valor extremo do tipo 1 parece bastante arbitrária, mas faz a matemática funcionar e pode ser possível justificar seu uso por meio da teoria da escolha racional .

Acontece que este modelo é equivalente ao modelo anterior, embora isso pareça não óbvio, uma vez que agora existem dois conjuntos de coeficientes de regressão e variáveis ​​de erro, e as variáveis ​​de erro têm uma distribuição diferente. Na verdade, este modelo se reduz diretamente ao anterior com as seguintes substituições:

${\ displaystyle {\ boldsymbol {\ beta}} = {\ boldsymbol {\ beta}} _ {1} - {\ boldsymbol {\ beta}} _ {0}}$

${\ displaystyle \ varepsilon = \ varepsilon _ {1} - \ varepsilon _ {0}}$

Uma intuição para isso vem do fato de que, como escolhemos com base no máximo de dois valores, apenas sua diferença importa, não os valores exatos - e isso efetivamente remove um grau de liberdade . Outro fato crítico é que a diferença de duas variáveis ​​distribuídas de valor extremo do tipo 1 é uma distribuição logística, ou seja, podemos demonstrar o equivalente da seguinte forma: ${\ displaystyle \ varepsilon = \ varepsilon _ {1} - \ varepsilon _ {0} \ sim \ operatorname {Logística} (0,1).}$

${\ displaystyle {\ begin {alinhado} \ Pr (Y_ {i} = 1 \ mid \ mathbf {X} _ {i}) = {} & \ Pr \ left (Y_ {i} ^ {1 \ ast}> Y_ {i} ^ {0 \ ast} \ mid \ mathbf {X} _ {i} \ right) & \\ [5pt] = {} & \ Pr \ left (Y_ {i} ^ {1 \ ast} - Y_ {i} ^ {0 \ ast}> 0 \ mid \ mathbf {X} _ {i} \ right) & \\ [5pt] = {} & \ Pr \ left ({\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i} + \ varepsilon _ {1} - \ left ({\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i} + \ psilon _ {0} \ direita)> 0 \ direita) & \\ [5pt] = {} & \ Pr \ left (({\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ { i} - {\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}) + (\ varepsilon _ {1} - \ varejpsilon _ {0})> 0 \ right) & \ \ [5pt] = {} & \ Pr (({\ boldsymbol {\ beta}} _ {1} - {\ boldsymbol {\ beta}} _ {0}) \ cdot \ mathbf {X} _ {i} + (\ varepsilon _ {1} - \ varepsilon _ {0})> 0) & \\ [5pt] = {} & \ Pr (({\ boldsymbol {\ beta}} _ {1} - {\ boldsymbol {\ beta}} _ {0}) \ cdot \ mathbf {X} _ {i} + \ varepsilon> 0) && {\ text {(substituir}} \ varejpsilon {\ text {como acima)}} \\ [5pt] = {} & \ Pr ({\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i} + \ varepsilon> 0) && {\ text {(substituir}} {\ boldsymbol {\ beta}} { \ text {como acima)}} \\ [5pt] = { } & \ Pr (\ varepsilon> - {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}) && {\ text {(agora, igual ao modelo acima)}} \\ [5pt] = {} & \ Pr (\ varepsilon <{\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}) & \\ [5pt] = {} & \ operatorname {logit} ^ {- 1} ( {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}) \\ [5pt] = {} & p_ {i} \ end {alinhado}}}$

Exemplo

Como exemplo, considere uma eleição em nível de província onde a escolha é entre um partido de centro-direita, um partido de centro-esquerda e um partido separatista (por exemplo, o Parti Québécois , que quer que Quebec se separe do Canadá ). Em seguida, usaríamos três variáveis ​​latentes, uma para cada escolha. Então, de acordo com a teoria da utilidade , podemos interpretar as variáveis ​​latentes como expressando a utilidade que resulta de fazer cada uma das escolhas. Também podemos interpretar os coeficientes de regressão como indicando a força que o fator associado (isto é, variável explicativa) tem em contribuir para a utilidade - ou mais corretamente, a quantidade pela qual uma mudança de unidade em uma variável explicativa muda a utilidade de uma dada escolha. Um eleitor pode esperar que o partido de centro-direita baixe os impostos, especialmente para os ricos. Isso não traria nenhum benefício às pessoas de baixa renda, ou seja, nenhuma mudança na utilidade (já que geralmente não pagam impostos); causaria benefício moderado (isto é, um pouco mais de dinheiro, ou aumento moderado de utilidade) para pessoas de meia renda; traria benefícios significativos para pessoas de alta renda. Por outro lado, pode-se esperar que o partido de centro-esquerda aumente os impostos e os compense com maior bem-estar e outras ajudas para as classes média e baixa. Isso causaria um benefício positivo significativo para pessoas de baixa renda, talvez um benefício fraco para pessoas de renda média e um benefício negativo significativo para pessoas de alta renda. Finalmente, o partido separatista não tomaria nenhuma ação direta sobre a economia, mas simplesmente se separaria. Um eleitor de baixa ou média renda pode não esperar basicamente nenhum ganho ou perda clara de utilidade com isso, mas um eleitor de alta renda pode esperar utilidade negativa, uma vez que é provável que possua empresas, o que terá mais dificuldade em fazer negócios em tal ambiente e provavelmente perder dinheiro.

Essas intuições podem ser expressas da seguinte forma:

Força estimada do coeficiente de regressão para diferentes resultados (escolhas de partido) e diferentes valores de variáveis ​​explicativas

	Centro-direita	Centro-esquerda	Secessionista
Alta renda	forte +	forte -	forte -
Renda média	moderado +	fraco +	Nenhum
Baixa renda	Nenhum	forte +	Nenhum

Isso mostra claramente que

1. Devem existir conjuntos separados de coeficientes de regressão para cada escolha. Quando formulado em termos de utilidade, isso pode ser visto muito facilmente. Escolhas diferentes têm efeitos diferentes na utilidade da rede; além disso, os efeitos variam de maneiras complexas que dependem das características de cada indivíduo; portanto, é necessário haver conjuntos separados de coeficientes para cada característica, não simplesmente uma única característica extra por escolha.
2. Embora a renda seja uma variável contínua, seu efeito sobre a utilidade é muito complexo para ser tratada como uma única variável. Ou ela precisa ser diretamente dividida em intervalos, ou é necessário adicionar poderes mais elevados de renda para que a regressão polinomial da renda seja efetivamente realizada.

Como um modelo "log-linear"

Ainda outra formulação combina a formulação de variável latente bidirecional acima com a formulação original acima, sem variáveis ​​latentes, e no processo fornece um link para uma das formulações padrão do logit multinomial .

Aqui, em vez de escrever o logit das probabilidades p _i como um preditor linear, separamos o preditor linear em dois, um para cada um dos dois resultados:

${\ displaystyle {\ begin {alinhados} \ ln \ Pr (Y_ {i} = 0) & = {\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i} - \ ln Z \\\ ln \ Pr (Y_ {i} = 1) & = {\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i} - \ ln Z \ end {alinhado}}}$

Observe que dois conjuntos separados de coeficientes de regressão foram introduzidos, assim como no modelo de variável latente bidirecional, e as duas equações aparecem em uma forma que escreve o logaritmo da probabilidade associada como um preditor linear, com um termo extra no final . Este termo, como se constatou, serve como o fator de normalização garantindo que o resultado seja uma distribuição. Isso pode ser visto exponenciando ambos os lados: ${\ displaystyle - \ ln Z}$

${\ displaystyle {\ begin {align} \ Pr (Y_ {i} = 0) & = {\ frac {1} {Z}} e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} \\ [5pt] \ Pr (Y_ {i} = 1) & = {\ frac {1} {Z}} e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}} \ end {alinhado}}}$

Desta forma, é claro que o propósito de Z é garantir que a distribuição resultante sobre Y _i seja de fato uma distribuição de probabilidade , ou seja, soma 1. Isso significa que Z é simplesmente a soma de todas as probabilidades não normalizadas, e dividindo cada probabilidade por Z , as probabilidades tornam-se " normalizadas ". Isso é:

${\ displaystyle Z = e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} + e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}}$

e as equações resultantes são

${\ displaystyle {\ begin {alinhados} \ Pr (Y_ {i} = 0) & = {\ frac {e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i }}} {e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} + e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}}} \\ [5pt] \ Pr (Y_ {i} = 1) & = {\ frac {e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}} {e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} + e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}}}. \ End {alinhado}}}$

Ou geralmente:

${\ displaystyle \ Pr (Y_ {i} = c) = {\ frac {e ^ {{\ boldsymbol {\ beta}} _ {c} \ cdot \ mathbf {X} _ {i}}} {\ sum _ {h} e ^ {{\ boldsymbol {\ beta}} _ {h} \ cdot \ mathbf {X} _ {i}}}}}$

Isso mostra claramente como generalizar essa formulação para mais de dois resultados, como no logit multinomial . Observe que esta formulação geral é exatamente a função softmax como em

${\ displaystyle \ Pr (Y_ {i} = c) = \ operatorname {softmax} (c, {\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}, {\ boldsymbol { \ beta}} _ {1} \ cdot \ mathbf {X} _ {i}, \ dots).}$

Para provar que isso é equivalente ao modelo anterior, observe que o modelo acima é especificado em excesso, e não pode ser especificado de forma independente: ao invés disso, saber que um determina automaticamente o outro. Como resultado, o modelo é não identificável , em que múltiplas combinações de β ₀ e β ₁ irão produzir as mesmas probabilidades para todas as variáveis ​​explicativas possíveis. Na verdade, pode-se ver que adicionar qualquer vetor constante a ambos produzirá as mesmas probabilidades: ${\ displaystyle \ Pr (Y_ {i} = 0)}$${\ displaystyle \ Pr (Y_ {i} = 1)}$${\ displaystyle \ Pr (Y_ {i} = 0) + \ Pr (Y_ {i} = 1) = 1}$

${\ displaystyle {\ begin {alinhado} \ Pr (Y_ {i} = 1) & = {\ frac {e ^ {({\ boldsymbol {\ beta}} _ {1} + \ mathbf {C}) \ cdot \ mathbf {X} _ {i}}} {e ^ {({\ boldsymbol {\ beta}} _ {0} + \ mathbf {C}) \ cdot \ mathbf {X} _ {i}} + e ^ {({\ boldsymbol {\ beta}} _ {1} + \ mathbf {C}) \ cdot \ mathbf {X} _ {i}}}} \\ [5pt] & = {\ frac {e ^ {{ \ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}} e ^ {\ mathbf {C} \ cdot \ mathbf {X} _ {i}}} {e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} e ^ {\ mathbf {C} \ cdot \ mathbf {X} _ {i}} + e ^ {{\ boldsymbol { \ beta}} _ {1} \ cdot \ mathbf {X} _ {i}} e ^ {\ mathbf {C} \ cdot \ mathbf {X} _ {i}}}} \\ [5pt] & = { \ frac {e ^ {\ mathbf {C} \ cdot \ mathbf {X} _ {i}} e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}} } {e ^ {\ mathbf {C} \ cdot \ mathbf {X} _ {i}} (e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} + e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}})}} \\ [5pt] & = {\ frac {e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}} {e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} + e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}}}. \ end {alinhado}} }$

Como resultado, podemos simplificar as coisas e restaurar a identificabilidade, escolhendo um valor arbitrário para um dos dois vetores. Escolhemos definir Então, ${\ displaystyle {\ boldsymbol {\ beta}} _ {0} = \ mathbf {0}.}$

${\ displaystyle e ^ {{\ boldsymbol {\ beta}} _ {0} \ cdot \ mathbf {X} _ {i}} = e ^ {\ mathbf {0} \ cdot \ mathbf {X} _ {i} } = 1}$

e entao

${\ displaystyle \ Pr (Y_ {i} = 1) = {\ frac {e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}} {1 + e ^ {{\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}}} = {\ frac {1} {1 + e ^ {- {\ boldsymbol {\ beta}} _ {1} \ cdot \ mathbf {X} _ {i}}}} = p_ {i}}$

o que mostra que esta formulação é de fato equivalente à formulação anterior. (Como na formulação da variável latente bidirecional, quaisquer configurações em que produzirão resultados equivalentes.) ${\ displaystyle {\ boldsymbol {\ beta}} = {\ boldsymbol {\ beta}} _ {1} - {\ boldsymbol {\ beta}} _ {0}}$

Observe que a maioria dos tratamentos do modelo logit multinomial começa estendendo a formulação "log-linear" apresentada aqui ou a formulação de variável latente bidirecional apresentada acima, uma vez que ambos mostram claramente a maneira como o modelo pode ser estendido para resultados. Em geral, a apresentação com variáveis ​​latentes é mais comum em econometria e ciência política , onde modelos de escolha discreta e teoria da utilidade reinam, enquanto a formulação "log-linear" aqui é mais comum em ciência da computação , por exemplo, aprendizado de máquina e processamento de linguagem natural .

Como um perceptron de camada única

O modelo tem uma formulação equivalente

${\ displaystyle p_ {i} = {\ frac {1} {1 + e ^ {- (\ beta _ {0} + \ beta _ {1} x_ {1, i} + \ cdots + \ beta _ {k } x_ {k, i})}}}. \,}$

Essa forma funcional é comumente chamada de perceptron de camada única ou rede neural artificial de camada única . Uma rede neural de camada única calcula uma saída contínua em vez de uma função de etapa . A derivada de p _i em relação a X  = ( x ₁ , ..., x _k ) é calculada a partir da forma geral:

${\ displaystyle y = {\ frac {1} {1 + e ^ {- f (X)}}}}$

em que f ( X ) é uma função analítica em X . Com essa escolha, a rede neural de camada única é idêntica ao modelo de regressão logística. Esta função possui uma derivada contínua, o que permite seu uso na retropropagação . Esta função também é preferida porque sua derivada é facilmente calculada:

${\ displaystyle {\ frac {\ mathrm {d} y} {\ mathrm {d} X}} = y (1-y) {\ frac {\ mathrm {d} f} {\ mathrm {d} X}} . \,}$

Em termos de dados binomiais

Um modelo intimamente relacionado assume que cada i está associado não a uma única tentativa de Bernoulli, mas a n _i tentativas independentes distribuídas de forma idêntica , onde a observação Y _i é o número de sucessos observados (a soma das variáveis ​​aleatórias individuais distribuídas de Bernoulli), e portanto, segue uma distribuição binomial :

${\ displaystyle Y_ {i} \, \ sim \ operatorname {Bin} (n_ {i}, p_ {i}), {\ text {for}} i = 1, \ pontos, n}$

Um exemplo desta distribuição é a fracção de sementes ( P _i ) que germinam após o n _i são plantadas.

Em termos de valores esperados , este modelo é expresso da seguinte forma:

${\ displaystyle p_ {i} = \ operatorname {\ mathcal {E}} \ left [\ left. {\ frac {Y_ {i}} {n_ {i}}} \, \ right | \, \ mathbf {X } _{eu certo]\,,}$

de modo a

${\ displaystyle \ operatorname {logit} \ left (\ operatorname {\ mathcal {E}} \ left [\ left. {\ frac {Y_ {i}} {n_ {i}}} \, \ right | \, \ mathbf {X} _ {i} \ right] \ right) = \ operatorname {logit} (p_ {i}) = \ ln \ left ({\ frac {p_ {i}} {1-p_ {i}}} \ right) = {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i} \ ,,}$

Ou equivalente:

${\ displaystyle \ Pr (Y_ {i} = y \ mid \ mathbf {X} _ {i}) = {n_ {i} \ escolha y} p_ {i} ^ {y} (1-p_ {i}) ^ {n_ {i} -y} = {n_ {i} \ escolha y} \ left ({\ frac {1} {1 + e ^ {- {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i}}}} \ right) ^ {y} \ left (1 - {\ frac {1} {1 + e ^ {- {\ boldsymbol {\ beta}} \ cdot \ mathbf {X} _ {i }}}} \ right) ^ {n_ {i} -y} \ ,.}$

Este modelo pode ser ajustado usando os mesmos tipos de métodos do modelo básico acima.

Bayesiano

Em um contexto de estatística bayesiana , as distribuições anteriores são normalmente colocadas nos coeficientes de regressão, geralmente na forma de distribuições gaussianas . Não há conjugado anterior da função de verossimilhança na regressão logística. Quando a inferência bayesiana foi realizada analiticamente, isso tornou a distribuição posterior difícil de calcular, exceto em dimensões muito baixas. Agora, porém, softwares automáticos como OpenBUGS , JAGS , PyMC3 , Stan ou Turing.jl permitem que esses posteriores sejam calculados usando simulação, portanto, a falta de conjugação não é uma preocupação. No entanto, quando o tamanho da amostra ou o número de parâmetros é grande, a simulação bayesiana completa pode ser lenta e as pessoas costumam usar métodos aproximados, como métodos bayesianos variacionais e propagação de expectativa .

História

Uma história detalhada da regressão logística é fornecida em Cramer (2002) . A função logística foi desenvolvida como modelo de crescimento populacional e denominada "logística" por Pierre François Verhulst nas décadas de 1830 e 1840, sob a orientação de Adolphe Quetelet ; consulte Função Logística § Histórico para obter detalhes. Em seu primeiro artigo (1838), Verhulst não especificou como ajustou as curvas aos dados. Em seu artigo mais detalhado (1845), Verhulst determinou os três parâmetros do modelo fazendo a curva passar por três pontos observados, o que produziu previsões ruins.

A função logística foi desenvolvida de forma independente na química como um modelo de autocatálise ( Wilhelm Ostwald , 1883). Uma reação autocatalítica é aquela em que um dos produtos é ele próprio um catalisador para a mesma reação, enquanto o fornecimento de um dos reagentes é fixo. Isso naturalmente dá origem à equação logística pela mesma razão do crescimento populacional: a reação é auto-reforçada, mas limitada.

A função logística foi redescoberta de forma independente como um modelo de crescimento populacional em 1920 por Raymond Pearl e Lowell Reed , publicado como Pearl & Reed (1920) , o que levou ao seu uso na estatística moderna. Inicialmente, eles desconheciam o trabalho de Verhulst e presumivelmente aprenderam sobre ele com L. Gustave du Pasquier , mas deram-lhe pouco crédito e não adotaram sua terminologia. A prioridade de Verhulst foi reconhecida e o termo "logística" revivido por Udny Yule em 1925 e tem sido seguido desde então. Pearl e Reed aplicaram primeiro o modelo à população dos Estados Unidos e também ajustaram inicialmente a curva fazendo-a passar por três pontos; como com Verhulst, isso novamente produziu resultados ruins. erro harvtxt: sem alvo: CITEREFPearlReed1920 ( ajuda )

Na década de 1930, o modelo probit foi desenvolvido e sistematizado por Chester Ittner Bliss , que cunhou o termo "probit" em Bliss (1934) , e por John Gaddum em Gaddum (1933) , e o modelo ajustado pela estimativa de máxima verossimilhança por Ronald A. Fisher em Fisher (1935) , como um adendo ao trabalho de Bliss. O modelo probit foi usado principalmente em bioensaios e foi precedido por trabalhos anteriores datados de 1860; veja o modelo Probit § História . O modelo probit influenciou o desenvolvimento subsequente do modelo logit e esses modelos competiram entre si. erro harvtxt: sem alvo: CITEREFBliss1934 ( ajuda )erro harvtxt: sem alvo: CITEREFGaddum1933 ( ajuda )erro harvtxt: sem alvo: CITEREFFisher1935 ( ajuda )

O modelo logístico provavelmente foi usado pela primeira vez como uma alternativa ao modelo probit em bioensaio por Edwin Bidwell Wilson e sua aluna Jane Worcester em Wilson & Worcester (1943) . No entanto, o desenvolvimento do modelo logístico como alternativa geral ao modelo probit deveu-se principalmente ao trabalho de Joseph Berkson ao longo de muitas décadas, começando em Berkson (1944) , onde cunhou "logit", por analogia com "probit", e continuando por Berkson (1951) e nos anos seguintes. O modelo logit foi inicialmente descartado como inferior ao modelo probit, mas "gradualmente alcançou uma posição de igualdade com o logit", particularmente entre 1960 e 1970. Em 1970, o modelo logit alcançou paridade com o modelo probit em uso em periódicos de estatística e posteriormente o ultrapassou. Essa popularidade relativa foi devido à adoção do logit fora do bioensaio, ao invés de deslocar o probit dentro do bioensaio, e seu uso informal na prática; a popularidade do logit é creditada à simplicidade computacional, propriedades matemáticas e generalidade do modelo logit, permitindo seu uso em campos variados. erro harvtxt: sem alvo: CITEREFBerkson1944 ( ajuda )erro harvtxt: sem alvo: CITEREFBerkson1951 ( ajuda )

Vários refinamentos ocorreram durante aquela época, notadamente por David Cox , como em Cox (1958) .

O modelo logit multinomial foi introduzido independentemente em Cox (1966) e Thiel (1969) , o que aumentou muito o escopo de aplicação e a popularidade do modelo logit. Em 1973, Daniel McFadden vinculou o logit multinomial à teoria da escolha discreta , especificamente o axioma da escolha de Luce , mostrando que o logit multinomial decorria do pressuposto de independência de alternativas irrelevantes e da interpretação das probabilidades de alternativas como preferências relativas; isso deu uma base teórica para a regressão logística.

Extensões

Há um grande número de extensões:

• A regressão logística multinomial (ou logit multinomial ) trata o caso de uma variável dependente categórica de múltiplas vias (com valores não ordenados, também chamada de "classificação"). Observe que o caso geral de ter variáveis ​​dependentes com mais de dois valores é denominado regressão politômica .
• A regressão logística ordenada (ou logit ordenado ) lida com variáveis ​​dependentes ordinais (valores ordenados).
• Logit misto é uma extensão de logit multinomial que permite correlações entre as escolhas da variável dependente.
• Uma extensão do modelo logístico para conjuntos de variáveis ​​interdependentes é o campo aleatório condicional .
• A regressão logística condicional lida com dados combinados ou estratificados quando os estratos são pequenos. É usado principalmente na análise de estudos observacionais .

Programas

A maioria dos softwares estatísticos pode fazer regressão logística binária.

• SPSS
  • [1] para regressão logística básica.
• Stata
• SAS
  • PROC LOGISTIC para regressão logística básica.
  • PROC CATMOD quando todas as variáveis ​​são categóricas.
  • PROC GLIMMIX para modelo de regressão logística multinível .
• R
  • glm no pacote de estatísticas (usando família = binomial)
  • lrmno pacote rms
  • Pacote GLMNET para uma implementação eficiente de regressão logística regularizada
  • lmer para regressão logística de efeitos mistos
  • Comando de pacote Rfast gm_logisticpara cálculos rápidos e pesados ​​envolvendo dados de grande escala.
  • pacote de braço para regressão logística bayesiana
• Pitão
  • Logitno módulo Statsmodels .
  • LogisticRegressionno módulo Scikit-learn .
  • LogisticRegressorno módulo TensorFlow .
  • Exemplo completo de regressão logística no tutorial Theano [2]
  • Regressão logística bayesiana com código anterior ARD , tutorial
  • Regressão logística variacional de Bayes com código anterior ARD , tutorial
  • Código de regressão logística bayesiana , tutorial
• NCSS
  • Regressão Logística em NCSS
• Matlab
  • mnrfitna caixa de ferramentas Estatísticas e aprendizado de máquina (com "incorreto" codificado como 2 em vez de 0)
  • fminunc/fmincon, fitglm, mnrfit, fitclinear, mle todos podem fazer regressão logística.
• Java ( JVM )
  • LibLinear
  • Apache Flink
  • Apache Spark
    • SparkML suporta regressão logística
• FPGA
  • Logistic Regresesion IP coreem HLS para FPGA .

Notavelmente, o pacote de extensão de estatísticas do Microsoft Excel não o inclui.

Veja também

• Função logística
• Escolha discreta
• Modelo Jarrow – Turnbull
• Variável dependente limitada
• Modelo logit multinomial
• Logit ordenado
• Teste Hosmer-Lemeshow
• Pontuação de Brier
• mlpack - contém uma implementação C ++ de regressão logística
• Amostragem caso-controle local
• Árvore do modelo logístico

Referências

Leitura adicional

links externos

• Mídia relacionada à regressão logística no Wikimedia Commons
• Aula de econometria (tópico: modelo Logit) no YouTube por Mark Thoma
• Tutorial de regressão logística
• mlelr : software em C para fins de ensino