Teoria lunar - Lunar theory

A teoria lunar tenta explicar os movimentos da lua . Existem muitas pequenas variações (ou perturbações ) no movimento da Lua, e muitas tentativas foram feitas para explicá-las. Depois de séculos sendo problemático, o movimento lunar agora é modelado com um alto grau de precisão (veja a seção Desenvolvimentos modernos ).

A teoria lunar inclui:

• o pano de fundo da teoria geral; incluindo técnicas matemáticas usadas para analisar o movimento da Lua e para gerar fórmulas e algoritmos para prever seus movimentos; e também
• fórmulas quantitativas, algoritmos e diagramas geométricos que podem ser usados ​​para calcular a posição da Lua em um determinado momento; frequentemente com a ajuda de tabelas baseadas nos algoritmos.

A teoria lunar tem uma história de mais de 2.000 anos de investigação. Seus desenvolvimentos mais modernos foram usados ​​nos últimos três séculos para fins científicos e tecnológicos fundamentais e ainda estão sendo usados ​​dessa forma.

Formulários

As aplicações da teoria lunar incluem o seguinte:

• No século XVIII, a comparação entre a teoria lunar e a observação foi usada para testar a lei da gravitação universal de Newton pelo movimento do apogeu lunar .
• Nos séculos XVIII e XIX, as tabelas de navegação baseadas na teoria lunar, inicialmente no Almanaque Náutico , foram muito utilizadas para a determinação da longitude no mar pelo método das distâncias lunares .
• No início do século XX, a comparação entre a teoria lunar e a observação foi usada em outro teste da teoria gravitacional, para testar (e descartar) a sugestão de Simon Newcomb de que uma discrepância bem conhecida no movimento do periélio de Mercúrio poderia ser explicado por um ajuste fracionário da potência -2 na lei da gravitação do inverso do quadrado de Newton (a discrepância foi posteriormente explicada com sucesso pela teoria da relatividade geral ).
• Em meados do século XX, antes do desenvolvimento dos relógios atômicos, a teoria lunar e a observação foram usadas em combinação para implementar uma escala de tempo astronômica ( tempo das efemérides ) livre das irregularidades do tempo solar médio.
• No final do século XX e início do século XXI, desenvolvimentos modernos da teoria lunar estão sendo usados ​​na série de modelos Jet Propulsion Laboratory Development Ephemeris do Sistema Solar, em conjunto com observações de alta precisão , para testar a exatidão das relações físicas associadas com a teoria geral da relatividade , incluindo o princípio de equivalência forte , gravitação relativística, precessão geodésica e a constância da constante gravitacional .

História

A Lua foi observada por milênios. Ao longo dessas idades, vários níveis de cuidado e precisão têm sido possíveis, de acordo com as técnicas de observação disponíveis a qualquer momento. Há uma história correspondentemente longa de teorias lunares: ela se estende desde os tempos dos astrônomos babilônios e gregos, até o laser lunar moderno.

Entre os notáveis ​​astrônomos e matemáticos ao longo dos tempos, cujos nomes estão associados às teorias lunares, estão:

Babilônico / caldeu

• Naburimannu
• Kidinnu
• Soudines

Grego / helenístico

• Hiparco
• Ptolomeu

árabe

• Ibn al-Shatir

Europeu, século 16 ao início do século 20

• Tycho Brahe
• Johannes Kepler
• Jeremiah Horrocks
• Ismaël Bullialdus
• John Flamsteed
• Isaac Newton
• Edmond Halley
• Leonhard Euler
• Alexis Clairaut
• Jean d'Alembert
• Tobias Mayer
• Johann Tobias Bürg
• Pierre-Simon Laplace
• Philippe le Doulcet
• Johann Karl Burckhardt
• Peter Andreas Hansen
• Charles-Eugène Delaunay
• John Couch Adams

América do Norte, século 19 ao início do século 20

• Simon Newcomb
• George William Hill
• Ernest William Brown
• Wallace John Eckert

Outros notáveis ​​matemáticos e astrônomos matemáticos também fizeram contribuições significativas.

A história pode ser considerada dividida em três partes: desde os tempos antigos até Newton; o período da física clássica (newtoniana); e desenvolvimentos modernos.

Tempos antigos para Newton

Babilônia

Sobre a astronomia babilônica , praticamente nada era conhecido dos historiadores da ciência antes da década de 1880. Os escritos antigos de Plínio sobreviventes fizeram menção simples de três escolas astronômicas na Mesopotâmia - na Babilônia, Uruk e 'Hipparenum' (possivelmente 'Sippar'). Mas o conhecimento moderno definitivo de todos os detalhes só começou quando Joseph Epping decifrou textos cuneiformes em tábuas de argila de um arquivo da Babilônia: Nesses textos, ele identificou uma efeméride de posições da lua. Desde então, o conhecimento do assunto, ainda fragmentário, teve que ser construído por meio da análise meticulosa de textos decifrados, principalmente na forma numérica, em tabuinhas de Babilônia e Uruk (nenhum traço ainda foi encontrado de qualquer coisa da terceira escola mencionada por Plínio).

Ao astrônomo babilônico Kidinnu (em grego ou latim, Kidenas ou Cidenas) foi atribuída a invenção (século V ou IV aC) do que hoje é chamado de "Sistema B" para prever a posição da lua, levando em consideração que a lua continuamente muda sua velocidade ao longo de seu caminho em relação ao plano de fundo de estrelas fixas. Este sistema envolvia o cálculo de mudanças graduais diárias da velocidade lunar, para cima ou para baixo, com um mínimo e um máximo aproximadamente a cada mês. A base desses sistemas parece ter sido aritmética em vez de geométrica, mas eles explicaram aproximadamente a principal desigualdade lunar agora conhecida como equação do centro .

Os babilônios mantiveram registros muito precisos de centenas de anos de novas luas e eclipses. Em algum momento entre os anos 500 aC e 400 aC, eles identificaram e começaram a usar a relação cíclica de 19 anos entre os meses lunares e os anos solares agora conhecida como ciclo metônico .

Isso os ajudou a construir uma teoria numérica das principais irregularidades no movimento da Lua, alcançando estimativas notavelmente boas para os (diferentes) períodos das três características mais proeminentes do movimento da Lua:

• O mês sinódico, ou seja, o período médio para as fases da lua. Agora chamado de "Sistema B", ele calcula o mês sinódico como 29 dias e (sexagesimalmente) 3,11; 0,50 "graus de tempo", onde cada grau de tempo é um grau do movimento aparente das estrelas, ou 4  minutos de tempo e os valores sexagesimais após o ponto-e-vírgula são frações de um grau de tempo. Isso se converte em 29,530594 dias = 29 ^d  12 ^h  44 ^m  3,33 ^s , para comparar com um valor moderno (em 1900 janeiro 0) de 29,530589 dias, ou 29 ^d  12 ^h  44 ^m  2,9 ^s . Este mesmo valor foi usado por Hiparco e Ptolomeu, foi usado ao longo da Idade Média e ainda constitui a base do calendário hebraico .
• A velocidade lunar média em relação às estrelas eles estimaram em 13 ° 10 ′ 35 ″ por dia, dando um mês correspondente de 27,321598 dias, para comparar com os valores modernos de 13 ° 10 ′ 35,0275 ″ e 27,321582 dias.
• O mês anomalístico, ou seja, o período médio para as acelerações e desacelerações mensais da Lua em sua taxa de movimento em relação às estrelas, teve uma estimativa babilônica de 27,5545833 dias, para comparar com um valor moderno de 27,554551 dias.
• O mês draconítico, ou seja, o período médio com o qual o caminho da Lua contra as estrelas desvia primeiro para o norte e depois para o sul na latitude eclíptica em comparação com o caminho da eclíptica do Sol, foi indicado por uma série de parâmetros diferentes que levam a várias estimativas, por exemplo, de 27,212204 dias, para comparar com um valor moderno de 27,212221, mas os babilônios também tinham uma relação numérica de que 5458 meses sinódicos eram iguais a 5923 meses draconíticos, que quando comparados com seu valor exato para o mês sinódico leva a praticamente exatamente o moderno figura para o mês draconítico.

A estimativa babilônica para o mês sinódico foi adotada durante a maior parte de dois milênios por Hiparco, Ptolomeu e escritores medievais (e ainda está em uso como parte da base para o calendário hebraico (judaico) calculado ).

Grécia e Egito Helenístico

Posteriormente, de Hiparco e Ptolomeu nas épocas Bitínia e Ptolomaica até a época da obra de Newton no século XVII, as teorias lunares foram compostas principalmente com a ajuda de idéias geométricas, inspiradas mais ou menos diretamente por longas séries de observações posicionais de a lua. Proeminente nessas teorias lunares geométricas eram as combinações de movimentos circulares - aplicações da teoria dos epiciclos.

Hiparco

Hipparchus , cujas obras se perderam em sua maioria e são conhecidas principalmente por citações de outros autores, presumiu que a Lua se movia em um círculo inclinado em 5 ° em relação à eclíptica , girando em uma direção retrógrada (ou seja, oposta à direção dos movimentos aparentes anuais e mensais de o Sol e a Lua em relação às estrelas fixas) uma vez em 18 2 ⁄ 3 anos. O círculo agia como um deferente, carregando um epiciclo ao longo do qual a Lua supostamente se movia em uma direção retrógrada. O centro do epiciclo se moveu a uma taxa correspondente à mudança média na longitude da Lua, enquanto o período da Lua ao redor do epiciclo foi um mês anômalo. Esse epiciclo fornecia aproximadamente o que mais tarde foi reconhecido como a desigualdade elíptica, a equação do centro , e seu tamanho se aproximava de uma equação do centro de cerca de 5 ° 1 '. Este valor é muito menor que o valor moderno : mas está próximo da diferença entre os coeficientes modernos da equação do centro (1º termo) e o da evecção : a diferença é explicada pelo fato de que as medidas antigas eram tomadas em tempos de eclipses, e o efeito da evecção (que subtrai, nessas condições, da equação do centro) era então desconhecido e esquecido. Para obter mais informações, consulte também o artigo separado Evecção .

Ptolomeu

A obra de Ptolomeu , o Almagesto, teve ampla e duradoura aceitação e influência por mais de um milênio. Ele apresentou uma teoria lunar geométrica que melhorou a de Hiparco ao fornecer uma segunda desigualdade do movimento da Lua, usando um dispositivo que fazia o apogeu aparente oscilar um pouco - a prosneusis do epiciclo. Essa segunda desigualdade ou segunda anomalia explicava aproximadamente, não apenas a equação do centro, mas também o que ficou conhecido (muito mais tarde) como evecção . Mas essa teoria, aplicada à sua conclusão lógica, faria com que a distância (e o diâmetro aparente) da Lua parecesse variar por um fator de cerca de 2, o que claramente não é visto na realidade. (O diâmetro angular aparente da Lua varia mensalmente, mas apenas em uma faixa muito mais estreita de cerca de 0,49 ° -0,55 °.) Este defeito da teoria ptolomaica levou a substituições propostas por Ibn al-Shatir no século 14 e por Copérnico no século 16.

Ibn al-Shatir e Copernicus

Avanços significativos na teoria lunar foram feitas pelo astrônomo árabe , Ibn al-Shatir  (1304-1375). Baseando-se na observação de que a distância à Lua não mudou tão drasticamente quanto exigido pelo modelo lunar de Ptolomeu, ele produziu um novo modelo lunar que substituiu o mecanismo de manivela de Ptolomeu por um modelo de epiciclo duplo que reduziu o intervalo computado de distâncias da Lua a partir do Terra. Uma teoria lunar semelhante, desenvolvida cerca de 150 anos mais tarde pelo astrônomo renascentista Nicolaus Copernicus , tinha a mesma vantagem em relação às distâncias lunares.

Tycho Brahe, Johannes Kepler e Jeremiah Horrocks

Tycho Brahe e Johannes Kepler refinaram a teoria lunar ptolomaica, mas não superaram seu defeito central de dar uma conta pobre das variações (principalmente mensais) na distância da Lua, diâmetro aparente e paralaxe . Seu trabalho acrescentou à teoria lunar três descobertas adicionais substanciais.

1. Os nós e a inclinação do plano orbital lunar parecem ambos librar , com um período mensal (de acordo com Tycho) ou semianual (de acordo com Kepler).
2. A longitude lunar tem uma variação bimestral , pela qual a Lua se move mais rápido do que o esperado na lua nova e cheia, e mais lento do que o esperado nos trimestres.
3. Há também um efeito anual, pelo qual o movimento lunar desacelera um pouco em janeiro e acelera um pouco em julho: a equação anual .

Os refinamentos de Brahe e Kepler foram reconhecidos por seus sucessores imediatos como melhorias, mas seus sucessores do século XVII tentaram numerosas configurações geométricas alternativas para os movimentos lunares para melhorar ainda mais as coisas. Um sucesso notável foi alcançado por Jeremiah Horrocks , que propôs um esquema envolvendo uma libração de aproximadamente 6 meses na posição do apogeu lunar e também no tamanho da excentricidade elíptica. Este esquema teve o grande mérito de fornecer uma descrição mais realista das mudanças na distância, diâmetro e paralaxe da Lua.

Newton

Um primeiro período gravitacional para a teoria lunar começou com o trabalho de Newton . Ele foi o primeiro a definir o problema do movimento perturbado da Lua em termos reconhecidamente modernos. Seu trabalho inovador é mostrado, por exemplo, nos Principia em todas as versões, incluindo a primeira edição publicada em 1687.

Perturbação solar do movimento lunar

Newton identificou como avaliar o efeito perturbador no movimento relativo da Terra e da Lua, decorrente de sua gravidade em direção ao Sol, no Livro 1, Proposição 66, e no Livro 3, Proposição 25. O ponto de partida para esta abordagem é o Corolário VI às leis do movimento. Isso mostra que se as forças aceleradoras externas de algum corpo massivo agirem igualmente e em paralelo em alguns outros corpos considerados diferentes, então esses corpos seriam afetados igualmente e, nesse caso, seus movimentos (em relação uns aos outros) continuariam como se não havia nenhuma dessas forças aceleradoras externas. É apenas no caso em que as forças externas (por exemplo, no Livro 1, Prop. 66 e no Livro 3, Prop. 25, as atrações gravitacionais em direção ao Sol) são diferentes em tamanho ou na direção em seus efeitos aceleradores nos diferentes corpos considerado (por exemplo, na Terra e na Lua), que os efeitos consequentes são apreciáveis ​​nos movimentos relativos dos últimos corpos. (Newton se referia a forças acelerativas ou gravidade acelerada devido a algum atrator massivo externo, como o Sol. A medida que ele usou foi a aceleração que a força tende a produzir (em termos modernos, força por unidade de massa), ao invés do que faríamos agora chame a própria força.)

Assim, Newton concluiu que é apenas a diferença entre a atração acelerativa do Sol na Lua e a atração do Sol na Terra que perturba o movimento da Lua em relação à Terra.

Newton então usou a decomposição vetorial de forças para realizar esta análise. No Livro 1, Proposição 66 e no Livro 3, Proposição 25, ele mostrou por uma construção geométrica, a partir da atração gravitacional total do Sol na Terra, e do Sol na Lua, a diferença que representa o efeito perturbador sobre o movimento da Lua em relação à Terra. Em resumo, a linha LS no diagrama de Newton conforme mostrado abaixo representa o tamanho e a direção da aceleração perturbadora agindo na Lua na posição atual da Lua P (a linha LS não passa pelo ponto P, mas o texto mostra que isso não se destina a ser significativo, é resultado dos fatores de escala e da forma como o diagrama foi construído).

Diagrama de Newton 'para encontrar a força do Sol para perturbar a Lua' que acompanha o Livro 3, Proposição 25 dos Principia

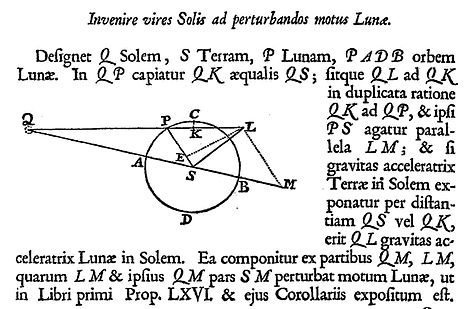
Aqui é mostrado o diagrama de Newton da primeira (1687) edição latina dos Principia (Livro 3, Proposição 25, p. 434). Aqui, ele introduziu sua análise de acelerações perturbadoras na Lua no sistema Sol-Terra-Lua. Q representa o Sol, S a Terra e P a Lua.

Partes deste diagrama representam distâncias, outras partes, acelerações gravitacionais (forças de atração por unidade de massa). Em um duplo significado, SQ representa a distância Terra-Sol, e então também representa o tamanho e a direção da aceleração gravitacional Terra-Sol. Outras distâncias no diagrama são então proporcionais à distância SQ. Outras atrações são proporcionais à atração SQ.

As atrações do Sol são SQ (na Terra) e LQ (na Lua). O tamanho de LQ é desenhado de forma que a proporção das atrações LQ: SQ seja o inverso do quadrado da proporção das distâncias PQ: SQ. (Newton constrói KQ = SQ, dando uma visão mais fácil das proporções.) A atração da Terra na Lua atua ao longo da direção PS. (Mas a linha PS significa apenas distância e direção até agora, nada foi definido sobre o fator de escala entre as atrações solar e terrestre).

Depois de mostrar as atrações solares LQ na Lua e SQ na Terra, na mesma escala, Newton então faz uma decomposição vetorial de LQ nos componentes LM e MQ. Em seguida, ele identifica a aceleração perturbadora na Lua como a diferença disso em relação ao SQ. SQ e MQ são paralelos um ao outro, então SQ pode ser subtraído diretamente de MQ, deixando MS. A diferença resultante, após subtrair SQ de LQ, é, portanto, a soma vetorial de LM e MS: somam-se a uma aceleração perturbadora LS.

Mais tarde, Newton identificou outra resolução da aceleração perturbadora LM + MS = LS, em componentes ortogonais: uma componente transversal paralela a LE e uma componente radial, efetivamente ES.

Representação alternativa de perturbações solares, vetores LS1 e LS2, como LS no diagrama de Newton acima, para 2 posições da Lua P em sua órbita ao redor da Terra S

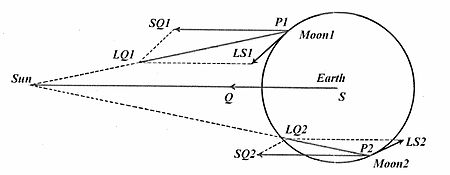
O esquema diagramático de Newton, desde sua época, foi reapresentado de outras maneiras, talvez visualmente mais claras. Aqui é mostrado uma apresentação vetorial indicando, para duas posições diferentes, P1 e P2, da Lua em sua órbita ao redor da Terra, os respectivos vetores LS1 e LS2 para a aceleração perturbadora devida ao Sol. A posição da Lua em P1 é bastante próxima da que estava em P no diagrama de Newton; a perturbação correspondente LS1 é como a LS de Newton em tamanho e direção. Em outra posição P2, a Lua está mais longe do Sol do que a Terra, a atração do Sol LQ2 na Lua é mais fraca do que a atração do Sol SQ = SQ2 na Terra, e então a perturbação resultante LS2 aponta obliquamente para longe do Sol .

Vetores de perturbação solar (setas) análogos a LS em muitas posições da Lua em sua órbita ao redor da Terra

Construções como as do diagrama de Newton podem ser repetidas para muitas posições diferentes da Lua em sua órbita. Para cada posição, o resultado é um vetor de perturbação como LS1 ou LS2 no segundo diagrama. Aqui é mostrada uma forma freqüentemente apresentada do diagrama que resume os tamanhos e direções dos vetores de perturbação para muitas posições diferentes da Lua em sua órbita. Cada pequena flecha é um vetor de perturbação como LS, aplicável à Lua na posição particular em torno da órbita de onde a flecha começa. As perturbações na Lua quando ela está quase alinhada ao longo do eixo Terra-Sol, ou seja, perto da lua nova ou cheia, apontam para fora, para longe da Terra. Quando a linha Lua-Terra está a 90 ° do eixo Terra-Sol, eles apontam para dentro, em direção à Terra, com um tamanho que é apenas metade do tamanho máximo das perturbações axiais (para fora). (Newton deu uma estimativa quantitativa bastante boa para o tamanho da força de perturbação solar: na quadratura, onde aumenta a atração da Terra, ele a colocou em 1 ⁄ 178,725 da atração terrestre média, e duas vezes mais do que no novo e completo luas onde se opõe e diminui a atração da Terra.)

Newton também mostrou que o mesmo padrão de perturbação se aplica, não só à Lua, em sua relação com a Terra perturbada pelo Sol, mas também a outras partículas de forma mais geral em sua relação com a Terra sólida perturbada pelo Sol (ou pela Lua); por exemplo, diferentes partes das águas das marés na superfície da Terra. O estudo do padrão comum dessas acelerações perturbadoras surgiu do estudo inicial de Newton sobre as perturbações da Lua, que ele também aplicou às forças que movem as águas das marés. Hoje em dia, esse padrão comum em si tornou-se frequentemente conhecido como força de maré, quer seja aplicado às perturbações dos movimentos da Lua ou das marés da Terra - ou dos movimentos de qualquer outro objeto que sofre perturbações de padrão análogo.

Depois de apresentar seu diagrama 'para encontrar a força do Sol para perturbar a Lua' no Livro 3, Proposição 25, Newton desenvolveu uma primeira aproximação para a força perturbadora solar, mostrando em mais detalhes como seus componentes variam conforme a Lua segue seu caminho mensal ao redor da Terra. Ele também deu os primeiros passos na investigação de como a força perturbadora mostra seus efeitos ao produzir irregularidades nos movimentos lunares.

Para algumas poucas desigualdades lunares selecionadas, Newton mostrou em alguns detalhes quantitativos como elas surgem da força perturbadora solar.

Muito desse trabalho lunar de Newton foi feito na década de 1680, e a extensão e precisão de seus primeiros passos na análise gravitacional foi limitada por vários fatores, incluindo sua própria escolha de desenvolver e apresentar o trabalho no que era, no todo, um caminho geométrico difícil, e pela precisão limitada e incerteza de muitas medições astronômicas em sua época.

Período gravitacional clássico após Newton

O principal objetivo dos sucessores de Newton, de Leonhard Euler , Alexis Clairaut e Jean d'Alembert em meados do século XVIII, até EW Brown no final do século XIX e início do século XX, era prestar contas completa e muito mais precisamente dos movimentos da lua com base nas leis de Newton, isto é, as leis do movimento e da gravitação universal por atrações inversamente proporcionais aos quadrados das distâncias entre os corpos atrativos. Eles também queriam colocar a lei da gravitação do inverso do quadrado à prova, e por um tempo na década de 1740 ela foi seriamente posta em dúvida, por conta do que então se pensava ser uma grande discrepância entre a teoria de Newton e as taxas observadas em o movimento do apogeu lunar. No entanto, Clairaut mostrou logo depois (1749-50) que pelo menos a principal causa da discrepância não estava na teoria lunar baseada nas leis de Newton, mas em aproximações excessivas nas quais ele e outros confiaram para avaliá-la.

A maioria das melhorias na teoria após Newton foram feitas na forma algébrica: envolviam quantidades volumosas e altamente laboriosas de cálculo infinitesimal e trigonometria. Também permaneceu necessário, para completar as teorias desse período, referir-se a medidas observacionais.

Resultados das teorias

Os teóricos lunares usaram (e inventaram) muitas abordagens matemáticas diferentes para analisar o problema gravitacional. Não é de surpreender que seus resultados tendam a convergir. Desde o tempo dos primeiros analistas gravitacionais entre os sucessores de Newton, Euler , Clairaut e d'Alembert , foi reconhecido que quase todas as principais perturbações lunares podiam ser expressas em termos de apenas alguns argumentos angulares e coeficientes. Eles podem ser representados por:

• os movimentos médios ou posições da Lua e do Sol, juntamente com três coeficientes e três posições angulares, que juntos definem a forma e a localização de suas órbitas aparentes:
• as duas excentricidades ( cerca de 0,0549 e cerca de 0,01675) das elipses que se aproximam das órbitas aparentes da Lua e do Sol;${\ displaystyle e}$${\ displaystyle e '}$
• a direção angular dos perigees ( e ) (ou seus pontos opostos os apogees) das duas órbitas; e${\ displaystyle \ Gamma}$${\ displaystyle \ Gamma '}$
• o ângulo de inclinação ( , valor médio de cerca de 18523 ") entre os planos das duas órbitas, junto com a direção ( ) da linha de nós em que esses dois planos se cruzam. O nó ascendente ( ) é o nó passado pela Lua quando está tendendo para o norte em relação à eclíptica.${\ displaystyle i}$${\ displaystyle \ Omega}$${\ displaystyle \ Omega}$

A partir desses parâmetros básicos, apenas quatro argumentos angulares diferenciais básicos são suficientes para expressar, em suas diferentes combinações, quase todas as perturbações mais significativas dos movimentos lunares. Eles são dados aqui com seus símbolos convencionais devido a Delaunay ; às vezes são conhecidos como argumentos Delaunay:

• ${\ displaystyle l}$a anomalia média da Lua (distância angular da longitude média da Lua em relação à longitude média de seu perigeu );${\ displaystyle \ Gamma}$
• ${\ displaystyle l '}$a anomalia média do Sol (distância angular da longitude média do Sol da longitude média de seu perigeu );${\ displaystyle \ Gamma '}$
• ${\ displaystyle F}$o argumento médio de latitude da Lua (distância angular da longitude média da Lua a partir da longitude média de seu nó ascendente (limite para o norte) );${\ displaystyle \ Omega}$
• ${\ displaystyle D}$ o alongamento médio (solar) da Lua (distância angular da longitude média da Lua da longitude média do Sol).

Este trabalho culminou na teoria lunar de Brown (1897–1908) e nas Tabelas do Movimento da Lua (1919). Estes foram usados ​​no American Ephemeris and Nautical Almanac até 1968, e em uma forma modificada até 1984.

Desigualdades lunares maiores ou nomeadas

Várias das maiores perturbações lunares na longitude (contribuições para a diferença em sua longitude eclíptica verdadeira em relação à sua longitude média) foram nomeadas. Em termos de argumentos diferenciais, eles podem ser expressos da seguinte forma, com coeficientes arredondados para o segundo mais próximo de arco ("):

Equação do centro

• A equação do centro da Lua, ou desigualdade elíptica, era conhecida pelo menos em aproximação pelos antigos, desde os babilônios e Hiparco em diante. O conhecimento de data mais recente é que corresponde à aplicação aproximada da lei de Kepler de áreas iguais em uma órbita elíptica, e representa a aceleração da Lua conforme sua distância da Terra diminui enquanto ela se move em direção ao seu perigeu, e então sua desaceleração à medida que sua distância da Terra aumenta enquanto se move em direção ao seu apogeu. O efeito na longitude da Lua pode ser aproximado por uma série de termos, dos quais os três primeiros são .${\ displaystyle +22639 '' \ sin (l) +769 '' \ sin (2l) +36 '' \ sin (3l)}$

Evecção

• A evecção (ou sua aproximação) era conhecida por Ptolomeu, mas seu nome e o conhecimento de sua causa datam do século XVII. Seu efeito na longitude da Lua tem um período de aparência estranha de cerca de 31,8 dias. Isso pode ser representado de várias maneiras, por exemplo, como o resultado de uma libração aproximada de 6 meses na posição do perigeu, com uma pulsação de 6 meses acompanhando no tamanho da excentricidade orbital da Lua. Seu termo principal é .${\ displaystyle +4586 '' \ sin (2D-l)}$

Variação

• A variação, descoberta por Tycho Brahe, é uma aceleração da Lua conforme ela se aproxima da lua nova e cheia, e uma desaceleração conforme se aproxima do primeiro e último quarto. Sua explicação gravitacional com estimativa quantitativa foi dada pela primeira vez por Newton. Seu termo principal é .${\ displaystyle +2370 '' \ sin (2D)}$

Equação anual

• A equação anual, também descoberta por Brahe, foi qualitativamente explicada por Newton em termos de que a órbita da Lua torna-se ligeiramente expandida em tamanho e mais longo em período, quando a Terra está no periélio mais próximo do Sol no início de janeiro, e a do Sol efeito perturbador é mais forte, e então ligeiramente contraído em tamanho e mais curto no período em que o Sol está mais distante no início de julho, de modo que seu efeito perturbador é mais fraco: o valor moderno para o termo principal devido a esse efeito é .${\ displaystyle -668 '' \ sin (l ')}$

Desigualdade paralática

• A desigualdade paralática, encontrada pela primeira vez por Newton, torna a Variação de Brahe um pouco assimétrica como resultado da distância finita e da paralaxe diferente de zero do Sol. Seu efeito é que a Lua está um pouco atrás no quarto minguante e um pouco adiante no quarto minguante. Seu termo principal é .${\ displaystyle -125 '' \ sin (D)}$

Redução à eclíptica

• A redução à eclíptica representa o efeito geométrico de expressar o movimento da Lua em termos de uma longitude no plano da eclíptica, embora seu movimento esteja realmente ocorrendo em um plano inclinado em cerca de 5 graus. Seu termo principal é .${\ displaystyle -412 '' \ sin (2F)}$

Os analistas de meados do século 18 expressaram as perturbações da posição da Lua em longitude usando cerca de 25-30 termos trigonométricos. No entanto, trabalhos nos séculos XIX e XX levaram a formulações muito diferentes da teoria, de modo que esses termos não são mais atuais. O número de termos necessários para expressar a posição da Lua com a precisão buscada no início do século XX era superior a 1400; e o número de termos necessários para emular a precisão das integrações numéricas modernas baseadas em observações de alcance a laser está na casa das dezenas de milhares: não há limite para o aumento no número de termos necessários à medida que os requisitos de precisão aumentam.

Desenvolvimentos modernos

Computadores digitais e laser lunar de alcance

O Laser Ranging Facility no Goddard Spaceflight Center

Desde a Segunda Guerra Mundial e especialmente a partir da década de 1960, a teoria lunar foi desenvolvida de uma maneira um tanto diferente. Isso foi estimulado de duas maneiras: por um lado, pelo uso de computação digital automática e, por outro lado, por tipos de dados observacionais modernos, com exatidão e precisão muito aumentadas.

Wallace John Eckert , aluno de Ernest William Brown , que trabalhou na IBM, usou os computadores digitais experimentais desenvolvidos lá após a Segunda Guerra Mundial para o cálculo de efemérides astronômicas. Um dos projetos era colocar a teoria lunar de Brown na máquina e avaliar as expressões diretamente. Outro projeto era algo totalmente novo: uma integração numérica das equações de movimento do Sol e dos quatro planetas principais. Isso se tornou viável somente depois que os computadores digitais eletrônicos tornaram-se disponíveis. Eventualmente, isso levou à série Jet Propulsion Laboratory Development Ephemeris .

Nesse ínterim, a teoria de Brown foi aprimorada com melhores constantes e a introdução de Ephemeris Time e a remoção de algumas correções empíricas associadas a isso. Isso levou à Improved Lunar Ephemeris (ILE), que, com algumas pequenas melhorias sucessivas, foi usada nos almanaques astronômicos de 1960 a 1983 e foi usada em missões de pouso lunar.

A melhoria mais significativa das observações da posição da Lua foram as medições de alcance do laser lunar , obtidas usando lasers ligados à Terra e retrorefletores especiais colocados na superfície da lua. O tempo de voo de um pulso de luz laser para um dos retrorrefletores e vice-versa dá uma medida da distância da Lua naquele momento. O primeiro dos cinco retrorrefletores que estão operacionais hoje foi levado à Lua na espaçonave Apollo 11 em julho de 1969 e colocado em uma posição adequada na superfície da Lua por Buzz Aldrin . A precisão do alcance foi ampliada ainda mais pela Operação de alcance a laser lunar do Observatório Apache Point , estabelecida em 2005.

Integrações numéricas, relatividade, marés, librações

A teoria lunar, desenvolvida numericamente para obter precisão fina usando essas medidas modernas, é baseada em uma gama maior de considerações do que as teorias clássicas: leva em consideração não apenas as forças gravitacionais (com correções relativísticas), mas também muitos efeitos de maré e geofísicos e uma teoria muito estendida da libração lunar . Como muitos outros campos científicos, este agora se desenvolveu de forma a se basear no trabalho de grandes equipes e instituições. Uma instituição que assumiu notavelmente um dos papéis principais nesses desenvolvimentos foi o Jet Propulsion Laboratory (JPL) no California Institute of Technology ; e nomes particularmente associados com a transição, do início dos anos 1970 em diante, das teorias lunares clássicas e efemérides para o estado moderno da ciência incluem os de J. Derral Mulholland e JG Williams, e para o desenvolvimento vinculado das efemérides do sistema solar (planetárias) E. Myles Standish.

Desde a década de 1970, o JPL produziu uma série de efemérides de desenvolvimento numericamente integradas (numeradas DExxx), incorporando efemérides lunares (LExxx). As efemérides planetárias e lunares DE200 / LE200 foram usadas nas efemérides oficiais do Almanaque Astronômico para 1984-2002, e as efemérides DE405 / LE405 , de maior exatidão e precisão, estão em uso desde a edição de 2003. A efeméride atual é DE440.

Desenvolvimentos analíticos

Paralelamente a esses desenvolvimentos, uma nova classe de teoria lunar analítica também foi desenvolvida nos últimos anos, notavelmente a Ephemeride Lunaire Parisienne de Jean Chapront e Michelle Chapront-Touzé do Bureau des Longitudes . Usando álgebra assistida por computador, os desenvolvimentos analíticos foram levados mais longe do que antes poderiam ser feitos pelos analistas clássicos trabalhando manualmente. Além disso, algumas dessas novas teorias analíticas (como ELP) foram ajustadas às efemérides numéricas anteriormente desenvolvidas no JPL, conforme mencionado acima. Os objetivos principais dessas teorias analíticas recentes, em contraste com os objetivos das teorias clássicas dos séculos anteriores, não têm sido gerar dados posicionais aprimorados para as datas atuais; em vez disso, seus objetivos incluíram o estudo de outros aspectos do movimento, como propriedades de longo prazo, que podem não ser tão facilmente aparentes nas próprias teorias numéricas modernas.

Notas

Referências

Bibliografia

• 'AE 1871': "Nautical Almanac & Astronomical Ephemeris" para 1871 , (Londres, 1867).
• EW Brown (1896). Um Tratado Introdutório à Teoria Lunar , Cambridge University Press.
• EW Brown. "Teoria do Movimento da Lua" , Memórias da Royal Astronomical Society , 53 (1897), 39-116.
• EW Brown. "Teoria do Movimento da Lua" , Memórias da Sociedade Astronômica Real , 53 (1899), 163–202.
• EW Brown. "Teoria do Movimento da Lua" , Memórias da Sociedade Astronômica Real , 54 (1900), 1-63.
• EW Brown. "Sobre a verificação da lei de Newton" , Monthly Notes of the Royal Astronomical Society 63 (1903), 396-397.
• EW Brown. "Teoria do Movimento da Lua" , Memórias da Sociedade Astronômica Real , 57 (1905), 51–145.
• EW Brown. "Teoria do Movimento da Lua" , Memórias da Royal Astronomical Society , 59 (1908), 1-103.
• EW Brown (1919). Tabelas do Movimento da Lua , New Haven.
• M Chapront-Touzé & J Chapront. "The lunar efemérides ELP-2000" , Astronomy & Astrophysics 124 (1983), 50-62.
• M Chapront-Touzé & J Chapront: "ELP2000-85: uma efeméride lunar semi-analítica adequada para tempos históricos" , Astronomy & Astrophysics 190 (1988), 342-352.
• M Chapront-Touzé & J Chapront, Efemérides Analíticas da Lua no Século XX (Observatoire de Paris, 2002).
• J Chapront; M Chapront-Touzé; G Francou. "Uma nova determinação de parâmetros orbitais lunares, constante de precessão e aceleração de maré de medições LLR" , Astronomy & Astrophysics 387 (2002), 700-709.
• J Chapront & G Francou. "A teoria lunar ELP revisitada. Introdução de novas perturbações planetárias" , Astronomy & Astrophysics 404 (2003), 735–742.
• IB Cohen e Anne Whitman (1999). Isaac Newton: 'The Principia', uma nova tradução , University of California Press. (Para obter detalhes bibliográficos, mas sem texto, consulte o link externo .)
• JO Dickey; PL Bender; JE Faller; e outros. "Lunar Laser Ranging: A Continuing Legacy of the Apollo Program" , Science 265 (1994), pp. 482-490.
• JLE Dreyer (1906). A History of Astronomy from Thales to Kepler , Cambridge University Press, (posteriormente republicado sob o título modificado "History of the Planetary Systems from Thales to Kepler").
• WJ Eckert et al. Improved Lunar Ephemeris 1952–1959: A Joint Supplement to the American Ephemeris and the (British) Nautical Almanac , (US Government Printing Office, 1954).
• J Epping e JN Strassmaier. "Zur Entzifferung der astronomischen Tafeln der Chaldaer" ("Sobre a decifração das tabelas astronômicas caldéias"), Stimmen aus Maria Laach , vol. 21 (1881), pp. 277–292.
• 'ESAE 1961': 'Suplemento explicativo para as efemérides astronômicas e as efemérides americanas e o almanaque náutico' ('preparado conjuntamente pelos escritórios do Almanaque náutico do Reino Unido e dos Estados Unidos da América'), Londres (HMSO), 1961.
• K Garthwaite; DB Holdridge e JD Mulholland. "Uma teoria preliminar de perturbação especial para o movimento lunar" , Astronomical Journal 75 (1970), 1133.
• H. Godfray (1885). Elementary Treatise on the Lunar Theory , Londres, (4ª ed.).
• Andrew Motte (1729a) (tradutor). "The Mathematical Principles of Natural Philosophy, de Sir Isaac Newton, traduzido para o inglês", Volume I, contendo o Livro 1 .
• Andrew Motte (1729b) (tradutor). "The Mathematical Principles of Natural Philosophy, de Sir Isaac Newton, traduzido para o inglês", Volume II, contendo os Livros 2 e 3 (com Índice, Apêndice contendo provas adicionais (Newtonianas) e "As Leis do Movimento da Lua de acordo com a Gravidade" , por John Machin).
• JD Mulholland e PJ Shelus. "Melhoria das efemérides lunares numéricas com dados de alcance do laser" , Moon 8 (1973), 532.
• O Neugebauer (1975). A History of Ancient Mathematical Astronomy , (em 3 volumes), New York (Springer).
• XX Newhall; EM Standish; JG Williams. "DE102: A efeméride numericamente integrada da Lua e planetas abrangendo quarenta e quatro séculos" , Astronomy and Astrophysics 125 (1983), 150.
• Observatório Naval dos EUA (2009). "História do Almanaque Astronômico" .
• JG Williams et al. "Fazendo soluções a partir de dados de alcance do laser lunar", Bulletin of the American Astronomical Society (1972), 4Q, 267.
• JG Williams; SG Turyshev; & DH Boggs. "Progress in Lunar Laser Ranging Tests of Relativistic Gravity" , Physical Review Letters , 93 (2004), 261101.