Cadeia de Markov - Markov chain

Parte de uma série de estatísticas
Teoria da probabilidade
Probabilidade Axiomas Determinismo Sistema Indeterminismo Aleatoriedade
Espaço de probabilidade Espaço amostral Evento Eventos coletivamente exaustivos Evento elementar Exclusividade mútua Resultado Singleton Experimentar Julgamento de Bernoulli Distribuição de probabilidade Distribuição Bernoulli Distribuição binomial Distribuição normal Medida de probabilidade Variável aleatória Processo Bernoulli Contínuo ou discreto Valor esperado Cadeia de Markov Valor observado Caminhada aleatória Processo estocástico
Evento complementar Probabilidade conjunta Probabilidade marginal Probabilidade Condicional
Independência Independência condicional Lei da probabilidade total Lei dos grandes números Teorema de Bayes Desigualdade de Boole
Diagrama de Venn Diagrama de árvore
v t e

Um diagrama que representa um processo de Markov de dois estados, com os estados rotulados como E e A. Cada número representa a probabilidade do processo de Markov mudar de um estado para outro, com a direção indicada pela seta. Por exemplo, se o processo de Markov está no estado A, então a probabilidade de ele mudar para o estado E é 0,4, enquanto a probabilidade de permanecer no estado A é 0,6.

Uma cadeia de Markov ou processo de Markov é um modelo estocástico que descreve uma sequência de eventos possíveis em que a probabilidade de cada evento depende apenas do estado alcançado no evento anterior. Uma sequência infinita contável , na qual a cadeia se move em intervalos de tempo discretos, fornece uma cadeia de Markov de tempo discreto (DTMC). Um processo de tempo contínuo é denominado cadeia de Markov de tempo contínuo (CTMC). Recebeu o nome do matemático russo Andrey Markov .

As cadeias de Markov têm muitas aplicações como modelos estatísticos de processos do mundo real, como estudar sistemas de controle de cruzeiro em veículos motorizados , filas ou filas de clientes que chegam a um aeroporto, taxas de câmbio e dinâmica da população animal.

Os processos de Markov são a base para métodos gerais de simulação estocástica conhecidos como cadeia de Markov Monte Carlo , que são usados ​​para simular a amostragem de distribuições de probabilidade complexas e têm aplicação em estatística Bayesiana , termodinâmica , mecânica estatística , física , química , economia , finanças , sinal processamento , teoria da informação e processamento da fala .

Os adjetivos Markoviano e Markov são usados ​​para descrever algo que está relacionado a um processo de Markov.

Introdução

Matemático russo Andrey Markov

Definição

Um processo de Markov é um processo estocástico que satisfaz a propriedade de Markov (às vezes caracterizado como " falta de memória "). Em termos mais simples, é um processo para o qual as previsões podem ser feitas sobre os resultados futuros com base apenas em seu estado atual e - o mais importante - tais previsões são tão boas quanto aquelas que poderiam ser feitas conhecendo a história completa do processo. Em outras palavras, dependendo do estado atual do sistema, seus estados futuro e passado são independentes .

Uma cadeia de Markov é um tipo de processo de Markov que tem um espaço de estado discreto ou um conjunto de índices discretos (geralmente representando o tempo), mas a definição precisa de uma cadeia de Markov varia. Por exemplo, é comum definir uma cadeia de Markov como um processo de Markov em tempo discreto ou contínuo com um espaço de estado contável (portanto, independentemente da natureza do tempo), mas também é comum definir uma cadeia de Markov como tendo tempo discreto no espaço de estado contável ou contínuo (portanto, independentemente do espaço de estado).

Tipos de cadeias de Markov

O espaço de estado do sistema e o índice do parâmetro de tempo precisam ser especificados. A tabela a seguir fornece uma visão geral das diferentes instâncias de processos de Markov para diferentes níveis de generalidade de espaço de estado e para tempo discreto vs. tempo contínuo:

Observe que não há acordo definitivo na literatura sobre o uso de alguns dos termos que significam casos especiais de processos de Markov. Normalmente, o termo "cadeia de Markov" é reservado para um processo com um conjunto discreto de tempos, ou seja, uma cadeia de Markov de tempo discreto (DTMC) , mas alguns autores usam o termo "processo de Markov" para se referir a um tempo contínuo Cadeia de Markov (CTMC) sem menção explícita. Além disso, existem outras extensões de processos de Markov que são referidos como tal, mas não necessariamente se enquadram em qualquer uma dessas quatro categorias (consulte o modelo de Markov ). Além disso, o índice de tempo não precisa necessariamente ter valor real; como acontece com o espaço de estados, existem processos concebíveis que se movem através de conjuntos de índices com outras construções matemáticas. Observe que a cadeia de Markov de tempo contínuo do espaço de estado geral é geral a tal ponto que não tem um termo designado.

Embora o parâmetro de tempo seja geralmente discreto, o espaço de estado de uma cadeia de Markov não tem nenhuma restrição geralmente aceita: o termo pode se referir a um processo em um espaço de estado arbitrário. No entanto, muitas aplicações de cadeias de Markov empregam espaços de estados finitos ou contáveis ​​infinitos , que têm uma análise estatística mais direta. Além dos parâmetros de índice de tempo e espaço de estado, existem muitas outras variações, extensões e generalizações (consulte Variações ). Para simplificar, a maior parte deste artigo se concentra no caso de tempo discreto e espaço de estado discreto, a menos que seja mencionado de outra forma.

Transições

As mudanças de estado do sistema são chamadas de transições. As probabilidades associadas a várias mudanças de estado são chamadas de probabilidades de transição. O processo é caracterizado por um espaço de estados, uma matriz de transição que descreve as probabilidades de transições específicas e um estado inicial (ou distribuição inicial) através do espaço de estados. Por convenção, presumimos que todos os estados e transições possíveis foram incluídos na definição do processo, portanto, há sempre um próximo estado e o processo não termina.

Um processo aleatório em tempo discreto envolve um sistema que está em um certo estado em cada etapa, com o estado mudando aleatoriamente entre as etapas. As etapas são frequentemente consideradas como momentos no tempo, mas podem igualmente se referir à distância física ou qualquer outra medida discreta. Formalmente, as etapas são inteiros ou números naturais , e o processo aleatório é um mapeamento deles para estados. A propriedade Markov afirma que a distribuição de probabilidade condicional para o sistema na próxima etapa (e de fato em todas as etapas futuras) depende apenas do estado atual do sistema e não adicionalmente do estado do sistema nas etapas anteriores.

Como o sistema muda aleatoriamente, geralmente é impossível prever com certeza o estado de uma cadeia de Markov em um determinado ponto no futuro. No entanto, as propriedades estatísticas do futuro do sistema podem ser previstas. Em muitas aplicações, são essas propriedades estatísticas que são importantes.

História

Markov estudou os processos de Markov no início do século 20, publicando seu primeiro artigo sobre o assunto em 1906. Os processos de Markov em tempo contínuo foram descobertos muito antes do trabalho de Andrey Markov no início do século 20 na forma do processo de Poisson . Markov estava interessado em estudar uma extensão de sequências aleatórias independentes, motivado por uma discordância com Pavel Nekrasov, que alegava que a independência era necessária para que a fraca lei dos grandes números se mantivesse. Em seu primeiro artigo sobre cadeias de Markov, publicado em 1906, Markov mostrou que, sob certas condições, os resultados médios da cadeia de Markov convergiriam para um vetor fixo de valores, provando assim uma lei fraca de grandes números sem a suposição de independência, que havia sido comumente considerado como um requisito para que tais leis matemáticas sejam válidas. Markov mais tarde usou cadeias de Markov para estudar a distribuição de vogais em Eugene Onegin , escrito por Alexander Pushkin , e provou ser um teorema de limite central para tais cadeias.

Em 1912, Henri Poincaré estudou cadeias de Markov em grupos finitos com o objetivo de estudar o embaralhamento de cartas. Outros usos iniciais das cadeias de Markov incluem um modelo de difusão, introduzido por Paul e Tatyana Ehrenfest em 1907, e um processo de ramificação, introduzido por Francis Galton e Henry William Watson em 1873, precedendo o trabalho de Markov. Após o trabalho de Galton e Watson, foi posteriormente revelado que seu processo de ramificação havia sido descoberto e estudado de forma independente cerca de três décadas antes por Irénée-Jules Bienaymé . A partir de 1928, Maurice Fréchet passou a se interessar pelas cadeias de Markov, o que acabou resultando na publicação em 1938 de um estudo detalhado sobre as cadeias de Markov.

Andrei Kolmogorov desenvolveu em um artigo de 1931 uma grande parte da teoria inicial dos processos de Markov de tempo contínuo. Kolmogorov foi parcialmente inspirado pelo trabalho de Louis Bachelier de 1900 sobre as flutuações no mercado de ações, bem como pelo trabalho de Norbert Wiener sobre o modelo de movimento browniano de Einstein. Ele introduziu e estudou um conjunto particular de processos de Markov conhecido como processos de difusão, onde derivou um conjunto de equações diferenciais que descrevem os processos. Independente do trabalho de Kolmogorov, Sydney Chapman derivou em um artigo de 1928 uma equação, agora chamada de equação de Chapman-Kolmogorov , de uma forma matematicamente menos rigorosa do que Kolmogorov, enquanto estudava o movimento browniano. As equações diferenciais são agora chamadas de equações de Kolmogorov ou equações de Kolmogorov-Chapman. Outros matemáticos que contribuíram significativamente para os fundamentos dos processos de Markov incluem William Feller , começando na década de 1930, e depois Eugene Dynkin , começando na década de 1950.

Exemplos

Passeios aleatórios baseados em inteiros e o problema da ruína do jogador são exemplos de processos de Markov. Algumas variações desses processos foram estudadas centenas de anos antes no contexto de variáveis ​​independentes. Dois exemplos importantes de processos de Markov são o processo de Wiener , também conhecido como processo de movimento browniano , e o processo de Poisson , que são considerados os processos estocásticos mais importantes e centrais na teoria dos processos estocásticos. Esses dois processos são processos de Markov em tempo contínuo, enquanto passeios aleatórios nos inteiros e o problema da ruína do jogador são exemplos de processos de Markov em tempo discreto.

Uma famosa cadeia de Markov é a chamada "caminhada do bêbado", uma caminhada aleatória na reta numérica onde, a cada passo, a posição pode mudar em +1 ou -1 com igual probabilidade. De qualquer posição, há duas transições possíveis, para o próximo inteiro ou para o inteiro anterior. As probabilidades de transição dependem apenas da posição atual, não da maneira como a posição foi alcançada. Por exemplo, as probabilidades de transição de 5 para 4 e de 5 para 6 são 0,5, e todas as outras probabilidades de transição de 5 são 0. Essas probabilidades são independentes se o sistema estava anteriormente em 4 ou 6.

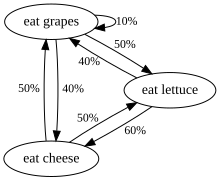
Outro exemplo são os hábitos alimentares de uma criatura que come apenas uvas, queijo ou alface e cujos hábitos alimentares obedecem às seguintes regras:

• Ele come exatamente uma vez por dia.
• Se comeu queijo hoje, amanhã comerá alface ou uvas com igual probabilidade.
• Se comeu uvas hoje, amanhã comerá uvas com probabilidade 1/10, queijo com probabilidade 4/10 e alface com probabilidade 5/10.
• Se comeu alface hoje, amanhã comerá uvas com probabilidade 4/10 ou queijo com probabilidade 6/10. Não comerá alface novamente amanhã.

Os hábitos alimentares dessa criatura podem ser modelados com uma cadeia de Markov, pois sua escolha amanhã depende exclusivamente do que ela comeu hoje, não do que comeu ontem ou em qualquer outro momento no passado. Uma propriedade estatística que pode ser calculada é a porcentagem esperada, ao longo de um longo período, dos dias em que a criatura comerá uvas.

Uma série de eventos independentes (por exemplo, uma série de cara ou coroa) satisfaz a definição formal de uma cadeia de Markov. No entanto, a teoria é geralmente aplicada apenas quando a distribuição de probabilidade da próxima etapa depende não trivialmente do estado atual.

Um exemplo não Markov

Suponha que haja um porta-moedas contendo cinco quartos (cada um valendo 25 ¢), cinco moedas (cada um valendo 10 ¢) e cinco níqueis (cada um valendo 5 ¢), e uma por uma, as moedas são retiradas aleatoriamente da bolsa e são colocado sobre uma mesa. Se representa o valor total das moedas colocadas na mesa após n sorteios, com , então a sequência não é um processo de Markov. ${\ displaystyle X_ {n}}$${\ displaystyle X_ {0} = 0}$${\ displaystyle \ {X_ {n}: n \ in \ mathbb {N} \}}$

Para ver por que esse é o caso, suponha que nos primeiros seis sorteios, todos os cinco níqueis e um quarto sejam sacados. Assim . Se soubermos não apenas , mas também os valores anteriores, poderemos determinar quais moedas foram sacadas e saberemos que a próxima moeda não será um níquel; portanto, podemos determinar isso com a probabilidade 1. Mas se não conhecermos os valores anteriores, com base apenas no valor, podemos supor que extraímos quatro moedas e duas moedas, caso em que certamente seria possível tirar outro níquel próximo. Assim, nossos palpites sobre são impactados por nosso conhecimento dos valores anteriores a . ${\ displaystyle X_ {6} = \ $ 0,50}$${\ displaystyle X_ {6}}$${\ displaystyle X_ {7} \ geq \ $ 0,60}$${\ displaystyle X_ {6}}$${\ displaystyle X_ {7}}$${\ displaystyle X_ {6}}$

No entanto, é possível modelar esse cenário como um processo de Markov. Em vez de definir para representar o valor total das moedas na mesa, poderíamos definir para representar a contagem dos vários tipos de moedas na mesa. Por exemplo, poderia ser definido para representar o estado onde há um quarto, zero centavos e cinco centavos na mesa após 6 sorteios um a um. Esse novo modelo seria representado por 216 estados possíveis (ou seja, 6x6x6 estados, já que cada um dos três tipos de moedas poderia ter de zero a cinco moedas na mesa ao final dos 6 sorteios). Suponha que o primeiro sorteio resulte em estado . A probabilidade de alcançar agora depende de ; por exemplo, o estado não é possível. Após o segundo sorteio, o terceiro sorteio depende de quais moedas foram sorteadas até agora, mas não mais apenas das moedas que foram sorteadas para o primeiro estado (uma vez que informações probabilisticamente importantes foram adicionadas ao cenário). Dessa forma, a probabilidade do estado depende exclusivamente do resultado do estado. ${\ displaystyle X_ {n}}$${\ displaystyle X_ {n}}$${\ displaystyle X_ {6} = 1,0,5}$${\ displaystyle X_ {1} = 0,1,0}$${\ displaystyle X_ {2}}$${\ displaystyle X_ {1}}$${\ displaystyle X_ {2} = 1,0,1}$${\ displaystyle X_ {n} = i, j, k}$${\ displaystyle X_ {n-1} = \ ell, m, p}$

Definição formal

Cadeia de Markov em tempo discreto

Uma cadeia de Markov de tempo discreto é uma sequência de variáveis ​​aleatórias X ₁ , X ₂ , X ₃ , ... com a propriedade de Markov , ou seja, que a probabilidade de passar para o próximo estado depende apenas do estado presente e não do anterior afirma:

${\ displaystyle \ Pr (X_ {n + 1} = x \ mid X_ {1} = x_ {1}, X_ {2} = x_ {2}, \ ldots, X_ {n} = x_ {n}) = \ Pr (X_ {n + 1} = x \ mid X_ {n} = x_ {n}),}$se ambas as probabilidades condicionais são bem definidas, isto é, se${\ displaystyle \ Pr (X_ {1} = x_ {1}, \ ldots, X_ {n} = x_ {n})> 0.}$

Os valores possíveis de X _i formam um conjunto contável S denominado espaço de estado da cadeia.

Variações

• Cadeias de Markov homogêneas no tempo são processos onde
  $${\ displaystyle \ Pr (X_ {n + 1} = x \ mid X_ {n} = y) = \ Pr (X_ {n} = x \ mid X_ {n-1} = y)}$$

  
  para todos n . A probabilidade da transição é independente de n .
• Cadeias de Markov estacionárias são processos onde
  $${\ displaystyle \ Pr (X_ {0} = x_ {0}, X_ {1} = x_ {1}, \ ldots, X_ {k} = x_ {k}) = \ Pr (X_ {n} = x_ { 0}, X_ {n + 1} = x_ {1}, \ ldots, X_ {n + k} = x_ {k})}$$

  
  para todo n e k . Cada cadeia estacionária pode ser comprovada como homogênea no tempo pela regra de Bayes.
  Uma condição necessária e suficiente para que uma cadeia de Markov homogênea no tempo seja estacionária é que a distribuição de seja uma distribuição estacionária da cadeia de Markov.${\ displaystyle X_ {0}}$
• Uma cadeia de Markov com memória (ou uma cadeia de Markov de ordem m ) onde m é finito, é um processo que satisfaz
  $${\ displaystyle {\ begin {alinhados} {} & \ Pr (X_ {n} = x_ {n} \ mid X_ {n-1} = x_ {n-1}, X_ {n-2} = x_ {n -2}, \ pontos, X_ {1} = x_ {1}) \\ = & \ Pr (X_ {n} = x_ {n} \ mid X_ {n-1} = x_ {n-1}, X_ {n-2} = x_ {n-2}, \ pontos, X_ {nm} = x_ {nm}) {\ text {para}} n> m \ end {alinhado}}}$$

  
  Em outras palavras, o estado futuro depende dos m estados anteriores. É possível construir uma cadeia a partir da qual tenha a propriedade 'clássica' de Markov tomando como espaço de estado as m- duplas ordenadas de valores de X , isto é ,.${\ displaystyle (Y_ {n})}$${\ displaystyle (X_ {n})}$${\ displaystyle Y_ {n} = \ left (X_ {n}, X_ {n-1}, \ ldots, X_ {n-m + 1} \ right)}$

Cadeia de Markov de tempo contínuo

Uma cadeia de Markov de tempo contínuo ( X _t ) _{t  ≥ 0} é definida por um espaço de estado finito ou contável S , uma matriz de taxa de transição Q com dimensões iguais àquela do espaço de estado e distribuição de probabilidade inicial definida no espaço de estado. Para i  ≠  j , os elementos q _ij são não negativos e descrevem a taxa das transições do processo do estado i para o estado j . Os elementos q _ii são escolhidos de forma que cada linha da matriz da taxa de transição some zero, enquanto as somas das linhas de uma matriz de transição de probabilidade em uma cadeia de Markov (discreta) são todas iguais a um.

Existem três definições equivalentes do processo.

Definição infinitesimal

A cadeia de Markov de tempo contínuo é caracterizada pelas taxas de transição, as derivadas em relação ao tempo das probabilidades de transição entre os estados i e j.

Seja a variável aleatória que descreve o estado do processo no tempo t , e suponha que o processo esteja em um estado i no tempo t . Então, saber , é independente dos valores anteriores , e como h → 0 para todo j e para todo t , ${\ displaystyle X_ {t}}$${\ displaystyle X_ {t} = i}$${\ displaystyle X_ {t + h} = j}$${\ displaystyle \ left (X_ {s}: s <t \ right)}$

${\ displaystyle \ Pr (X (t + h) = j \ mid X (t) = i) = \ delta _ {ij} + q_ {ij} h + o (h)}$,

onde está o delta de Kronecker , usando a notação little-o . O pode ser visto como uma medição da rapidez com que a transição de i para j acontece. ${\ displaystyle \ delta _ {ij}}$${\ displaystyle q_ {ij}}$

Definição de cadeia de salto / tempo de espera

Definir um tempo discreto Markov cadeia Y _n para descrever o n th salto do processo e as variáveis S ₁ , S ₂ , S ₃ , ... para descrever tempos de retenção em cada um dos estados em que S _i segue a distribuição exponencial com taxa parâmetro - q _{Y i Y i} .

Definição de probabilidade de transição

Para qualquer valor n = 0, 1, 2, 3, ... e tempos indexados até este valor de n : t ₀ , t ₁ , t ₂ , ... e todos os estados registrados nesses tempos i ₀ , i ₁ , i ₂ , i ₃ , ... sustenta que

${\ displaystyle \ Pr (X_ {t_ {n + 1}} = i_ {n + 1} \ mid X_ {t_ {0}} = i_ {0}, X_ {t_ {1}} = i_ {1}, \ ldots, X_ {t_ {n}} = i_ {n}) = p_ {i_ {n} i_ {n + 1}} (t_ {n + 1} -t_ {n})}$

onde p _ij é a solução da equação direta (uma equação diferencial de primeira ordem )

${\ displaystyle P '(t) = P (t) Q}$

com a condição inicial P (0) é a matriz de identidade .

Espaço de estado finito

Se o espaço de estados for finito , a distribuição de probabilidade de transição pode ser representada por uma matriz , chamada de matriz de transição, com o ( i , j ) o elemento de P igual a

${\ displaystyle p_ {ij} = \ Pr (X_ {n + 1} = j \ mid X_ {n} = i).}$

Uma vez que cada linha de P soma um e todos os elementos são não negativos, P é uma matriz estocástica direita .

Relação de distribuição estacionária para autovetores e simplicos

Uma distribuição estacionária π é um vetor (linha), cujas entradas não são negativas e somam 1, é inalterado pela operação da matriz de transição P sobre ele e, portanto, é definido por

${\ displaystyle \ pi \ mathbf {P} = \ pi.}$

Ao comparar esta definição com a de um autovetor , vemos que os dois conceitos estão relacionados e que

${\ displaystyle \ pi = {\ frac {e} {\ sum _ {i} {e_ {i}}}}}$

é um múltiplo normalizado ( ) de um autovetor esquerdo e da matriz de transição P com um autovalor de 1. Se houver mais de um autovetor unitário, então uma soma ponderada dos estados estacionários correspondentes também é um estado estacionário. Mas, para uma cadeia de Markov, geralmente está mais interessado em um estado estacionário que é o limite da sequência de distribuições para alguma distribuição inicial. ${\ textstyle \ sum _ {i} \ pi _ {i} = 1}$

Os valores de uma distribuição estacionária estão associados ao espaço de estados de P e seus autovetores têm suas proporções relativas preservadas. Como as componentes de π são positivas e a restrição de que sua soma é a unidade pode ser reescrita , visto que o produto escalar de π com um vetor cujas componentes são todas 1 é unidade e que π está em um simplex . ${\ displaystyle \ textstyle \ pi _ {i}}$${\ textstyle \ sum _ {i} 1 \ cdot \ pi _ {i} = 1}$

Cadeia de Markov homogênea no tempo com um espaço de estado finito

Se a cadeia de Markov for homogênea no tempo, a matriz de transição P é a mesma após cada etapa, de modo que a probabilidade de transição da etapa k pode ser calculada como a potência k da matriz de transição, P ^k .

Se a cadeia de Markov for irredutível e aperiódica, então haverá uma distribuição estacionária única π . Além disso, neste caso P ^k converge para uma matriz de classificação em que cada linha é a distribuição estacionária π :

${\ displaystyle \ lim _ {k \ to \ infty} \ mathbf {P} ^ {k} = \ mathbf {1} \ pi}$

onde 1 é o vetor coluna com todas as entradas iguais a 1. Isso é declarado pelo teorema de Perron-Frobenius . Se, por qualquer meio, for encontrada, então a distribuição estacionária da cadeia de Markov em questão pode ser facilmente determinada para qualquer distribuição inicial, como será explicado abaixo. ${\ textstyle \ lim _ {k \ to \ infty} \ mathbf {P} ^ {k}}$

Para algumas matrizes estocásticas P , o limite não existe enquanto a distribuição estacionária existe, como mostrado por este exemplo: ${\ textstyle \ lim _ {k \ to \ infty} \ mathbf {P} ^ {k}}$

${\ displaystyle \ mathbf {P} = {\ begin {pmatrix} 0 & 1 \\ 1 & 0 \ end {pmatrix}} \ qquad \ mathbf {P} ^ {2k} = I \ qquad \ mathbf {P} ^ {2k + 1 } = \ mathbf {P}}$

${\ displaystyle {\ begin {pmatrix} {\ frac {1} {2}} & {\ frac {1} {2}} \ end {pmatrix}} {\ begin {pmatrix} 0 & 1 \\ 1 & 0 \ end {pmatrix }} = {\ begin {pmatrix} {\ frac {1} {2}} & {\ frac {1} {2}} \ end {pmatrix}}}$

(Este exemplo ilustra uma cadeia de Markov periódica.)

Como há vários casos especiais diferentes a serem considerados, o processo de encontrar esse limite, se ele existir, pode ser uma tarefa demorada. No entanto, existem muitas técnicas que podem ajudar a encontrar esse limite. Vamos P ser um n × n matriz, e definir${\ textstyle \ mathbf {Q} = \ lim _ {k \ to \ infty} \ mathbf {P} ^ {k}.}$

É sempre verdade que

${\ displaystyle \ mathbf {QP} = \ mathbf {Q}.}$

Subtraindo Q de ambos os lados e fatorando, então, resulta

${\ displaystyle \ mathbf {Q} (\ mathbf {P} - \ mathbf {I} _ {n}) = \ mathbf {0} _ {n, n},}$

onde I _n é a matriz identidade de tamanho n e 0 _{n , n} é a matriz zero de tamanho n × n . Multiplicar matrizes estocásticas sempre resulta em outra matriz estocástica, então Q deve ser uma matriz estocástica (veja a definição acima). Às vezes é suficiente para usar a equação matriz acima eo fato de que Q é uma matriz estocástica para resolver para Q . Incluindo o fato de que a soma de cada uma das linhas em P é 1, existem n + 1 equações para determinar n incógnitas, então é computacionalmente mais fácil se por um lado selecionar uma linha em Q e substituir cada um de seus elementos por um , e em outros substitutos um elemento correspondente (a uma na mesma coluna) no vector de 0 , e deixou-se multiplica próximo deste último vector pelo inverso do ex matriz transformada para encontrar Q .

Aqui está um método para fazer isso: primeiro, defina a função f ( A ) para retornar a matriz A com sua coluna mais à direita substituída por todos os 1s. Se [ f ( P - I _n )] ⁻¹ existe, então

${\ displaystyle \ mathbf {Q} = f (\ mathbf {0} _ {n, n}) [f (\ mathbf {P} - \ mathbf {I} _ {n})] ^ {- 1}.}$

Explique: A equação da matriz original é equivalente a um sistema de n × n equações lineares em n × n variáveis. E há mais n equações lineares a partir do fato de que Q é uma matriz estocástica direita em que cada linha soma 1. Portanto, ela precisa de quaisquer n × n equações lineares independentes das equações (n × n + n) para resolver o n × n variáveis. Neste exemplo, as n equações de “Q multiplicado pela coluna mais à direita de (P-In)” foram substituídas pelas n equações estocásticas.

Uma coisa a notar é que se P tem um elemento P _{i , i} em sua diagonal principal que é igual a 1 e a i- ésima linha ou coluna é preenchida com 0's, então essa linha ou coluna permanecerá inalterada em todas as poderes P ^k . Assim, a i -ésima linha ou coluna de Q terá os 1 e os 0 de nas mesmas posições como em P .

Velocidade de convergência para a distribuição estacionária

Como afirmado anteriormente, a partir da equação (se existir) a estacionário (ou estado estacionário) distribuição π é um vector próprio esquerda da linha matriz estocástica P . Então, supondo que P é diagonalizável ou equivalentemente que P tem n autovetores linearmente independentes, a velocidade de convergência é elaborada como segue. (Para matrizes não diagonalizáveis, ou seja, defeituosas , pode-se começar com a forma normal de Jordan de P e prosseguir com um conjunto um pouco mais complicado de argumentos de maneira semelhante. ${\ displaystyle {\ boldsymbol {\ pi}} = {\ boldsymbol {\ pi}} \ mathbf {P},}$

Seja U a matriz dos autovetores (cada um normalizado para ter uma norma L2 igual a 1) onde cada coluna é um autovetor esquerdo de P e seja Σ a matriz diagonal dos autovalores esquerdos de P , ou seja, Σ = diag ( λ ₁ , λ ₂ , λ ₃ , ..., λ _n ). Então, por eigendecomposition

${\ displaystyle \ mathbf {P} = \ mathbf {U \ Sigma U} ^ {- 1}.}$

Deixe os valores próprios serem enumerados de forma que:

${\ displaystyle 1 = | \ lambda _ {1} |> | \ lambda _ {2} | \ geq | \ lambda _ {3} | \ geq \ cdots \ geq | \ lambda _ {n} |.}$

Como P é uma matriz estocástica de linha, seu maior autovalor esquerdo é 1. Se houver uma distribuição estacionária única, o maior autovalor e o autovetor correspondente também serão únicos (porque não há outro π que resolva a equação de distribuição estacionária acima). Seja u _i a i -ésima coluna da matriz U , ou seja, u _i é o autovetor esquerdo de P correspondendo a λ _i . Além disso, seja x um vetor de comprimento n linhas que representa uma distribuição de probabilidade válida; uma vez que os vectores próprios u _i abrangem podemos escrever ${\ displaystyle \ mathbb {R} ^ {n},}$

${\ displaystyle \ mathbf {x} ^ {\ mathsf {T}} = \ sum _ {i = 1} ^ {n} a_ {i} \ mathbf {u} _ {i}, \ qquad a_ {i} \ em \ mathbb {R}.}$

Se multiplicarmos x por P da direita e continuarmos esta operação com os resultados, no final obtemos a distribuição estacionária π . Em outras palavras, π = u _i ← xPP ... P = xP ^k como k → ∞. Que significa

${\ displaystyle {\ begin {align} {\ boldsymbol {\ pi}} ^ {(k)} & = \ mathbf {x} \ left (\ mathbf {U \ Sigma U} ^ {- 1} \ right) \ esquerda (\ mathbf {U \ Sigma U} ^ {- 1} \ direita) \ cdots \ esquerda (\ mathbf {U \ Sigma U} ^ {- 1} \ direita) \\ & = \ mathbf {xU \ Sigma} ^ {k} \ mathbf {U} ^ {- 1} \\ & = \ left (a_ {1} \ mathbf {u} _ {1} ^ {\ mathsf {T}} + a_ {2} \ mathbf { u} _ {2} ^ {\ mathsf {T}} + \ cdots + a_ {n} \ mathbf {u} _ {n} ^ {\ mathsf {T}} \ right) \ mathbf {U \ Sigma} ^ {k} \ mathbf {U} ^ {- 1} \\ & = a_ {1} \ lambda _ {1} ^ {k} \ mathbf {u} _ {1} ^ {\ mathsf {T}} + a_ {2} \ lambda _ {2} ^ {k} \ mathbf {u} _ {2} ^ {\ mathsf {T}} + \ cdots + a_ {n} \ lambda _ {n} ^ {k} \ mathbf {u} _ {n} ^ {\ mathsf {T}} && u_ {i} \ bot u_ {j} {\ text {para}} i \ neq j \\ & = \ lambda _ {1} ^ {k} \ left \ {a_ {1} \ mathbf {u} _ {1} ^ {\ mathsf {T}} + a_ {2} \ left ({\ frac {\ lambda _ {2}} {\ lambda _ {1 }}} \ right) ^ {k} \ mathbf {u} _ {2} ^ {\ mathsf {T}} + a_ {3} \ left ({\ frac {\ lambda _ {3}} {\ lambda _ {1}}} \ right) ^ {k} \ mathbf {u} _ {3} ^ {\ mathsf {T}} + \ cdots + a_ {n} \ left ({\ frac {\ lambda _ {n} } {\ lambda _ {1}}} \ right) ^ {k} \ mathbf {u} _ {n} ^ {\ mathsf {T}} \ right \} \ end {alinhado}}}$

Como π = u ₁ , π ^{( k ) se} aproxima de π quando k → ∞ com uma velocidade da ordem de λ ₂ / λ ₁ exponencialmente. Isso ocorre porque, portanto, λ ₂ / λ ₁ é o termo dominante. Quanto menor for a proporção, mais rápida será a convergência. O ruído aleatório na distribuição de estado π também pode acelerar essa convergência para a distribuição estacionária. ${\ displaystyle | \ lambda _ {2} | \ geq \ cdots \ geq | \ lambda _ {n} |,}$

Espaço de estado geral

Correntes Harris

Muitos resultados para cadeias de Markov com espaço de estado finito podem ser generalizados para cadeias com espaço de estado incontável por meio de cadeias de Harris .

O uso de cadeias de Markov em métodos de Monte Carlo por cadeias de Markov cobre casos em que o processo segue um espaço de estado contínuo.

Cadeias de Markov de interação local

Considerando uma coleção de cadeias de Markov cuja evolução leva em conta o estado de outras cadeias de Markov, está relacionado à noção de cadeias de Markov interagindo localmente . Isso corresponde à situação em que o espaço de estado tem uma forma de produto (cartesiana). Veja sistema de partículas interagentes e autômatos celulares estocásticos (autômatos celulares probabilísticos). Veja, por exemplo, Interação de Processos de Markov ou

Propriedades

Dois estados se comunicam entre si se ambos forem alcançáveis ​​um do outro por uma sequência de transições com probabilidade positiva. Esta é uma relação de equivalência que produz um conjunto de classes comunicantes. Uma turma é fechada se a probabilidade de deixar a turma for zero. Uma cadeia de Markov é irredutível se houver uma classe de comunicação, o espaço de estado.

Um estado i tem ponto final se é o maior divisor comum do número de transições pelas quais i pode ser alcançado, a partir de i . Isso é: ${\ displaystyle k}$${\ displaystyle k}$

${\ displaystyle k = \ gcd \ {n> 0: \ Pr (X_ {n} = i \ mid X_ {0} = i)> 0 \}}$

Um estado i é considerado transitório se, partindo de i , houver uma probabilidade diferente de zero de que a cadeia nunca retornará a i . Caso contrário, é recorrente. Para um estado recorrente i , o tempo médio de acerto é definido como:

${\ displaystyle M_ {i} = E [T_ {i}] = \ sum _ {n = 1} ^ {\ infty} n \ cdot f_ {ii} ^ {(n)}.}$

O estado i é recorrente positivo se for finito e recorrente nulo em caso contrário. Periodicidade, transitoriedade, recorrência e recorrência positiva e nula são propriedades de classe - ou seja, se um estado tem a propriedade, então todos os estados em sua classe de comunicação têm a propriedade. ${\ displaystyle M_ {i}}$

Um estado i é denominado absorvente se não houver transições de saída do estado.

Ergodicidade

Um estado i é considerado ergódico se for aperiódico e recorrente positivo. Em outras palavras, um estado i é ergódico se for recorrente, tem um período de 1 e tem tempo de recorrência médio finito. Se todos os estados em uma cadeia de Markov irredutível são ergódicos, então a cadeia é dita ergódica.

Pode-se mostrar que uma cadeia de Markov irredutível de estado finito é ergódica se tiver um estado aperiódico. Mais geralmente, uma cadeia de Markov é ergodic se existe um número N de tal modo que qualquer estado pode ser atingido a partir de qualquer outro estado em qualquer número de etapas inferior ou igual a um número N . No caso de uma matriz de transição totalmente conectada, onde todas as transições têm uma probabilidade diferente de zero, esta condição é atendida com  N  = 1.

Uma cadeia de Markov com mais de um estado e apenas uma transição de saída por estado não é irredutível ou não aperiódica, portanto, não pode ser ergódica.

Representações Markovianas

Em alguns casos, processos aparentemente não markovianos ainda podem ter representações markovianas, construídas pela expansão do conceito de estados 'atuais' e 'futuros'. Por exemplo, seja X um processo não Markoviano. Em seguida, define um processo de Y , de modo a que cada estado de Y representa um intervalo de tempo dos estados de X . Matematicamente, isso assume a forma:

${\ displaystyle Y (t) = {\ big \ {} X (s): s \ in [a (t), b (t)] \, {\ big \}}.}$

Se Y tem a propriedade de Markov, então é uma representação Markoviana de X .

Um exemplo de um processo não Markoviano com uma representação Markoviana é uma série temporal autoregressiva de ordem maior que um.

Tempos de acerto

O tempo de acerto é o tempo, começando em um determinado conjunto de estados até que a cadeia chegue em um determinado estado ou conjunto de estados. A distribuição de tal período de tempo tem uma distribuição do tipo de fase. A distribuição mais simples é a de uma única transição distribuída exponencialmente.

Tempos de acerto esperados

Para um subconjunto de estados A  ⊆  S , o vetor k ^A de tempos de acerto (onde o elemento representa o valor esperado , começando no estado i em que a cadeia entra em um dos estados no conjunto A ) é a solução não negativa mínima para ${\ displaystyle k_ {i} ^ {A}}$

${\ displaystyle {\ begin {alinhado} k_ {i} ^ {A} = 0 & {\ text {for}} i \ in A \\ - \ sum _ {j \ in S} q_ {ij} k_ {j} ^ {A} = 1 & {\ text {para}} i \ notin A. \ end {alinhado}}}$

Inversão de tempo

Para um CTMC X _t , o processo reverso no tempo é definido como sendo . De acordo com o lema de Kelly, esse processo tem a mesma distribuição estacionária que o processo direto. ${\ displaystyle {\ hat {X}} _ {t} = X_ {Tt}}$

Uma cadeia é considerada reversível se o processo reverso for igual ao processo de encaminhamento. O critério de Kolmogorov afirma que a condição necessária e suficiente para um processo ser reversível é que o produto das taxas de transição em torno de uma malha fechada deve ser o mesmo em ambas as direções.

Cadeia de Markov incorporada

Um método para encontrar a distribuição de probabilidade estacionária , π , de uma cadeia de Markov de tempo contínuo ergódico , Q , é primeiro encontrar sua cadeia de Markov embutida (EMC) . A rigor, o EMC é uma cadeia de Markov de tempo discreto regular, às vezes chamada de processo de salto . Cada elemento da matriz de probabilidade de transição de uma etapa do EMC, S , é denotado por s _ij e representa a probabilidade condicional de transição do estado i para o estado j . Essas probabilidades condicionais podem ser encontradas por

${\ displaystyle s_ {ij} = {\ begin {cases} {\ frac {q_ {ij}} {\ sum _ {k \ neq i} q_ {ik}}} & {\ text {if}} i \ neq j \\ 0 & {\ text {caso contrário}}. \ end {cases}}}$

A partir disso, S pode ser escrito como

${\ displaystyle S = I- \ left (\ operatorname {diag} (Q) \ right) ^ {- 1} Q}$

onde I é a matriz identidade e diag ( Q ) é a matriz diagonal formada selecionando a diagonal principal da matriz Q e definindo todos os outros elementos como zero.

Para encontrar o vetor de distribuição de probabilidade estacionária, devemos em seguida encontrar tal que ${\ displaystyle \ varphi}$

${\ displaystyle \ varphi S = \ varphi,}$

com sendo um vector da linha, de tal modo que todos os elementos em são maiores do que 0 e = 1. A partir deste, π pode ser encontrado como ${\ displaystyle \ varphi}$${\ displaystyle \ varphi}$${\ displaystyle \ | \ varphi \ | _ {1}}$

${\ displaystyle \ pi = {- \ varphi (\ operatorname {diag} (Q)) ^ {- 1} \ over \ left \ | \ varphi (\ operatorname {diag} (Q)) ^ {- 1} \ right \ | _ {1}}.}$

( S pode ser periódico, mesmo que Q não seja. Uma vez que π é encontrado, ele deve ser normalizado para um vetor unitário .)

Outro processo de tempo discreto que pode ser derivado de uma cadeia de Markov de tempo contínuo é um esqueleto δ - a cadeia de Markov (de tempo discreto) formada observando X ( t ) em intervalos de unidades de tempo δ. As variáveis ​​aleatórias X (0),  X (δ),  X (2δ), ... fornecem a sequência de estados visitados pelo esqueleto δ.

Tipos especiais de cadeias de Markov

Modelo de Markov

Os modelos de Markov são usados ​​para modelar sistemas em mudança. Existem 4 tipos principais de modelos, que generalizam cadeias de Markov dependendo se cada estado sequencial é observável ou não, e se o sistema deve ser ajustado com base nas observações feitas:

Esquema de Bernoulli

Um esquema de Bernoulli é um caso especial de uma cadeia de Markov onde a matriz de probabilidade de transição tem linhas idênticas, o que significa que o próximo estado é independente até mesmo do estado atual (além de ser independente dos estados anteriores). Um esquema de Bernoulli com apenas dois estados possíveis é conhecido como processo de Bernoulli .

Observe, entretanto, pelo teorema do isomorfismo de Ornstein , que toda cadeia de Markov aperiódica e irredutível é isomórfica a um esquema de Bernoulli; assim, pode-se igualmente afirmar que as cadeias de Markov são um "caso especial" de esquemas de Bernoulli. O isomorfismo geralmente requer uma recodificação complicada. O teorema do isomorfismo é ainda um pouco mais forte: ele afirma que qualquer processo estocástico estacionário é isomórfico a um esquema de Bernoulli; a cadeia de Markov é apenas um exemplo.

Subshift de tipo finito

Quando a matriz de Markov é substituída pela matriz de adjacência de um grafo finito , o deslocamento resultante é denominado uma cadeia de Markov topológica ou um subshift de tipo finito . Uma matriz de Markov compatível com a matriz de adjacência pode fornecer uma medida no subshift. Muitos sistemas dinâmicos caóticos são isomórficos às cadeias de Markov topológicas; exemplos incluem Difeomorfismos de variedade fechada , o sistema Prouhet-Thue-Morse , o sistema Chacon , sistemas sofic , sistemas livres de contexto e sistemas de codificação de bloco .

Formulários

A pesquisa relatou a aplicação e a utilidade das cadeias de Markov em uma ampla gama de tópicos, como física, química, biologia, medicina, música, teoria dos jogos e esportes.

Física

Os sistemas markovianos aparecem extensivamente na termodinâmica e na mecânica estatística , sempre que as probabilidades são usadas para representar detalhes desconhecidos ou não modelados do sistema, se pode ser assumido que a dinâmica é invariável no tempo e que nenhuma história relevante precisa ser considerada que já não esteja incluída na descrição do estado. Por exemplo, um estado termodinâmico opera sob uma distribuição de probabilidade que é difícil ou cara de adquirir. Portanto, o método Markov Chain Monte Carlo pode ser usado para extrair amostras aleatoriamente de uma caixa preta para aproximar a distribuição de probabilidade de atributos em uma gama de objetos.

Os caminhos, na formulação integral de caminhos da mecânica quântica, são cadeias de Markov.

As cadeias de Markov são usadas em simulações de QCD em rede .

Química

${\ displaystyle {\ ce {{E} + {\ underset {Substrato \ na ligação superior} {S <=> E}} {\ overset {Catalítico \ na etapa superior} {S-> E}} + P}}}$

Cinética de Michaelis-Menten . A enzima (E) se liga a um substrato (S) e produz um produto (P). Cada reação é uma transição de estado em uma cadeia de Markov.

Uma rede de reação é um sistema químico que envolve múltiplas reações e espécies químicas. Os modelos estocásticos mais simples de tais redes tratam o sistema como uma cadeia de Markov de tempo contínuo com o estado sendo o número de moléculas de cada espécie e com reações modeladas como possíveis transições da cadeia. Cadeias de Markov e processos de Markov de tempo contínuo são úteis em química quando os sistemas físicos se aproximam da propriedade de Markov. Por exemplo, imagine um grande número n de moléculas em solução no estado A, cada uma das quais pode sofrer uma reação química no estado B com uma certa taxa média. Talvez a molécula seja uma enzima, e os estados se referem a como ela é dobrada. O estado de qualquer enzima segue uma cadeia de Markov e, como as moléculas são essencialmente independentes umas das outras, o número de moléculas no estado A ou B por vez é n vezes a probabilidade de uma determinada molécula estar nesse estado.

O modelo clássico de atividade enzimática, a cinética de Michaelis-Menten , pode ser visto como uma cadeia de Markov, onde a cada passo de tempo a reação prossegue em alguma direção. Embora Michaelis-Menten seja bastante direto, redes de reação muito mais complicadas também podem ser modeladas com cadeias de Markov.

Um algoritmo baseado em uma cadeia de Markov também foi usado para focar o crescimento baseado em fragmentos de produtos químicos in silico em direção a uma classe desejada de compostos, como drogas ou produtos naturais. À medida que uma molécula cresce, um fragmento é selecionado da molécula nascente como o estado "atual". Não está ciente de seu passado (isto é, não está ciente do que já está ligado a ele). Em seguida, ele passa para o próximo estado quando um fragmento é anexado a ele. As probabilidades de transição são treinadas em bancos de dados de classes autênticas de compostos.

Além disso, o crescimento (e composição) de copolímeros podem ser modelados usando cadeias de Markov. Com base nas razões de reatividade dos monômeros que compõem a cadeia de polímero em crescimento, a composição da cadeia pode ser calculada (por exemplo, se os monômeros tendem a adicionar de forma alternada ou em longas execuções do mesmo monômero). Devido aos efeitos estéricos , os efeitos de Markov de segunda ordem também podem desempenhar um papel no crescimento de algumas cadeias de polímero.

Da mesma forma, foi sugerido que a cristalização e o crescimento de alguns materiais de óxido de super- rede epitaxial podem ser descritos com precisão por cadeias de Markov.

Biologia

As cadeias de Markov são usadas em várias áreas da biologia. Exemplos notáveis ​​incluem:

• Filogenética e bioinformática , em que a maioria dos modelos de evolução do DNA usa cadeias de Markov de tempo contínuo para descrever o nucleotídeo presente em um determinado local do genoma .
• Dinâmica populacional , onde as cadeias de Markov são em particular uma ferramenta central no estudo teórico de modelos de matriz populacional .
• Neurobiologia , onde cadeias de Markov foram usadas, por exemplo, para simular o neocórtex de mamíferos.
• Biologia de sistemas , por exemplo, com a modelagem de infecção viral de células individuais.
• Modelos compartimentais para surto de doenças e modelagem epidêmica.

Testando

Vários teóricos propuseram a ideia do teste estatístico de cadeia de Markov (MCST), um método de conjugação de cadeias de Markov para formar uma " manta de Markov ", organizando essas cadeias em várias camadas recursivas ("wafering") e produzindo conjuntos de testes mais eficientes - amostras —Como um substituto para testes exaustivos. MCSTs também têm usos em redes baseadas em estados temporais; O artigo de Chilukuri et al. Intitulado "Redes de raciocínio de incerteza temporal para fusão de evidências com aplicativos para detecção e rastreamento de objetos" (ScienceDirect) fornece um histórico e um estudo de caso para a aplicação de MCSTs em uma gama mais ampla de aplicações.

Variabilidade da irradiância solar

As avaliações da variabilidade da irradiância solar são úteis para aplicações de energia solar . A variabilidade da irradiância solar em qualquer local ao longo do tempo é principalmente uma consequência da variabilidade determinística do caminho do sol através da cúpula do céu e da variabilidade na nebulosidade. A variabilidade da irradiância solar acessível na superfície da Terra foi modelada usando cadeias de Markov, incluindo também a modelagem dos dois estados de claro e nebuloso como uma cadeia de Markov de dois estados.

Reconhecimento de fala

Os modelos ocultos de Markov são a base da maioria dos sistemas de reconhecimento automático de voz modernos.

Teoria da informação

Cadeias de Markov são usadas em todo o processamento de informações. O famoso artigo de Claude Shannon , de 1948, A Mathematical Theory of Communication , que em uma única etapa criou o campo da teoria da informação , abre apresentando o conceito de entropia por meio da modelagem de Markov da língua inglesa. Esses modelos idealizados podem capturar muitas das regularidades estatísticas dos sistemas. Mesmo sem descrever a estrutura completa do sistema perfeitamente, esses modelos de sinal podem tornar possível a compressão de dados muito eficaz por meio de técnicas de codificação de entropia , como a codificação aritmética . Eles também permitem uma estimativa de estado eficaz e reconhecimento de padrões . As cadeias de Markov também desempenham um papel importante na aprendizagem por reforço .

Cadeias de Markov também são a base para modelos de Markov ocultos, que são uma ferramenta importante em diversos campos como redes telefônicas (que usam o algoritmo de Viterbi para correção de erros), reconhecimento de voz e bioinformática (como na detecção de rearranjos).

O algoritmo de compressão de dados sem perdas LZMA combina cadeias de Markov com compressão Lempel-Ziv para atingir taxas de compressão muito altas.

Teoria de filas

As cadeias de Markov são a base para o tratamento analítico de filas ( teoria das filas ). Agner Krarup Erlang iniciou o assunto em 1917. Isso os torna críticos para otimizar o desempenho das redes de telecomunicações, onde as mensagens muitas vezes competem por recursos limitados (como largura de banda).

Numerosos modelos de filas usam cadeias de Markov de tempo contínuo. Por exemplo, uma fila M / M / 1 é um CTMC nos inteiros não negativos onde as transições ascendentes de i para i  + 1 ocorrem na taxa λ de acordo com um processo de Poisson e descrevem chegadas de trabalho, enquanto as transições de i para i  - 1 (para i  > 1) ocorrem na taxa μ (os tempos de serviço do trabalho são distribuídos exponencialmente) e descrevem os serviços concluídos (partidas) da fila.

Aplicativos de internet

Um diagrama de estado que representa o algoritmo PageRank com uma probabilidade de transição de M ou .${\ displaystyle {\ frac {\ alpha} {k_ {i}}} + {\ frac {1- \ alpha} {N}}}$

O PageRank de uma página da web usado pelo Google é definido por uma cadeia de Markov. É a probabilidade de estar na página da distribuição estacionária na seguinte cadeia de Markov em todas as páginas da web (conhecidas). Se for o número de páginas da web conhecidas e uma página tiver links para ela, então ela terá probabilidade de transição para todas as páginas que estão vinculadas e para todas as páginas que não estão vinculadas. O parâmetro é considerado como cerca de 0,15. ${\ displaystyle i}$${\ displaystyle N}$${\ displaystyle i}$${\ displaystyle k_ {i}}$${\ displaystyle {\ frac {\ alpha} {k_ {i}}} + {\ frac {1- \ alpha} {N}}}$${\ displaystyle {\ frac {1- \ alpha} {N}}}$${\ displaystyle \ alpha}$

Modelos de Markov também têm sido usados ​​para analisar o comportamento de navegação na web dos usuários. A transição de um link da web de um usuário em um site específico pode ser modelada usando modelos Markov de primeira ou segunda ordem e pode ser usada para fazer previsões sobre navegação futura e personalizar a página da web para um usuário individual.

Estatisticas

Os métodos de cadeia de Markov também se tornaram muito importantes para gerar sequências de números aleatórios para refletir com precisão distribuições de probabilidade desejadas muito complicadas, por meio de um processo chamado cadeia de Markov Monte Carlo (MCMC). Nos últimos anos, isso revolucionou a praticabilidade dos métodos de inferência bayesiana , permitindo que uma ampla gama de distribuições posteriores sejam simuladas e seus parâmetros encontrados numericamente.

Economia e finanças

As cadeias de Markov são usadas em finanças e economia para modelar uma variedade de fenômenos diferentes, incluindo a distribuição de renda, a distribuição do tamanho das empresas, preços de ativos e quedas de mercado. DG Champernowne construiu um modelo de cadeia de Markov da distribuição de renda em 1953. Herbert A. Simon e o co-autor Charles Bonini usaram um modelo de cadeia de Markov para derivar uma distribuição Yule estacionária de tamanhos de empresas. Louis Bachelier foi o primeiro a observar que os preços das ações seguiam uma caminhada aleatória. O passeio aleatório foi mais tarde visto como evidência a favor da hipótese do mercado eficiente e os modelos de passeio aleatório eram populares na literatura da década de 1960. Modelos de mudança de regime de ciclos de negócios foram popularizados por James D. Hamilton (1989), que usou uma cadeia de Markov para modelar mudanças entre períodos de crescimento de PIB alto e baixo (ou alternativamente, expansões e recessões econômicas). Um exemplo mais recente é o modelo multifractal de troca de Markov de Laurent E. Calvet e Adlai J. Fisher, que se baseia na conveniência dos modelos de troca de regime anteriores. Ele usa uma cadeia de Markov arbitrariamente grande para impulsionar o nível de volatilidade dos retornos de ativos.

A macroeconomia dinâmica faz uso intenso de cadeias de Markov. Um exemplo é o uso de cadeias de Markov para modelar exogenamente os preços das ações (ações) em um cenário de equilíbrio geral .

As agências de classificação de crédito produzem tabelas anuais das probabilidades de transição para títulos de diferentes classificações de crédito.

Ciências Sociais

As cadeias de Markov são geralmente usadas na descrição de argumentos dependentes do caminho , onde as configurações estruturais atuais condicionam os resultados futuros. Um exemplo é a reformulação da idéia, originalmente devido a Karl Marx 's Das Kapital , amarrando o desenvolvimento econômico com a ascensão do capitalismo . Na pesquisa atual, é comum usar uma cadeia de Markov para modelar como uma vez que um país atinge um nível específico de desenvolvimento econômico, a configuração de fatores estruturais, como tamanho da classe média , a proporção de residência urbana para rural, a taxa de mobilização política , etc., irá gerar uma maior probabilidade de transição do regime autoritário para o democrático .

Jogos

As cadeias de Markov podem ser usadas para modelar muitos jogos de azar. Os jogos infantis Snakes and Ladders e " Hi Ho! Cherry-O ", por exemplo, são representados exatamente por cadeias de Markov. Em cada turno, o jogador começa em um determinado estado (em um determinado quadrado) e a partir daí tem chances fixas de mover-se para outros estados (quadrados).

Música

As cadeias de Markov são empregadas na composição de música algorítmica , particularmente em softwares como Csound , Max e SuperCollider . Em uma cadeia de primeira ordem, os estados do sistema tornam-se valores de notas ou tons, e um vetor de probabilidade para cada nota é construído, completando uma matriz de probabilidade de transição (veja abaixo). Um algoritmo é construído para produzir valores de notas de saída com base nas ponderações da matriz de transição, que podem ser valores de notas MIDI , frequência ( Hz ) ou qualquer outra métrica desejável.

Uma cadeia de Markov de segunda ordem pode ser introduzida considerando o estado atual e também o estado anterior, conforme indicado na segunda tabela. Mais elevadas, n ° de ordem cadeias tendem a "grupo" notas particulares em conjunto, enquanto 'romper' em outros padrões e sequências ocasionalmente. Essas cadeias de ordem superior tendem a gerar resultados com um senso de estrutura frasal , em vez da "perambulação sem objetivo" produzida por um sistema de primeira ordem.

As cadeias de Markov podem ser usadas estruturalmente, como no Analogique A e B. de Xenakis. As cadeias de Markov também são usadas em sistemas que usam um modelo de Markov para reagir interativamente à entrada de música.

Normalmente, os sistemas musicais precisam impor restrições de controle específicas nas sequências de comprimento finito que geram, mas as restrições de controle não são compatíveis com os modelos de Markov, uma vez que induzem dependências de longo alcance que violam a hipótese de Markov de memória limitada. Para superar essa limitação, uma nova abordagem foi proposta.

Beisebol

Modelos de cadeia de Markov têm sido usados ​​em análises avançadas de beisebol desde 1960, embora seu uso ainda seja raro. Cada meia entrada de um jogo de beisebol se encaixa no estado da cadeia de Markov quando o número de corredores e eliminados é considerado. Durante qualquer rebatida, existem 24 combinações possíveis de número de outs e posição dos corredores. Mark Pankin mostra que os modelos de cadeia de Markov podem ser usados ​​para avaliar corridas criadas tanto para jogadores individuais quanto para uma equipe. Ele também discute vários tipos de estratégias e condições de jogo: como os modelos de cadeia de Markov têm sido usados ​​para analisar estatísticas de situações de jogo como bunting e roubo de base e diferenças ao jogar na grama contra o AstroTurf .

Geradores de texto Markov

Os processos de Markov também podem ser usados ​​para gerar um texto superficialmente real, dado um documento de amostra. Os processos de Markov são usados ​​em uma variedade de softwares recreativos de " gerador de paródia " (ver dissociated press , Jeff Harrison, Mark V. Shaney e Academias Neutronium ). Existem várias bibliotecas de geração de texto de código aberto usando cadeias de Markov, incluindo o RiTa Toolkit .

Previsão probabilística

As cadeias de Markov têm sido usadas para previsões em várias áreas: por exemplo, tendências de preços, energia eólica e irradiância solar. Os modelos de previsão da cadeia de Markov utilizam uma variedade de configurações, desde a discretização da série temporal até modelos de Markov ocultos combinados com wavelets e o modelo de distribuição de mistura da cadeia de Markov (MCM).

Veja também

Notas

Referências

links externos