Problema de fluxo máximo - Maximum flow problem

Rede de fluxo para o problema: Cada ser humano (r i ) está disposto a adotar um gato (w i 1) e / ou um cachorro (w i 2). No entanto, cada animal de estimação (p i ) tem preferência por apenas um subconjunto dos humanos. Encontre qualquer correspondência de animais de estimação com humanos de forma que o número máximo de animais de estimação seja adotado por um de seus humanos preferidos.

Na teoria de otimização , os problemas de fluxo máximo envolvem encontrar um fluxo viável através de uma rede de fluxo que obtenha a taxa de fluxo máxima possível.

O problema de fluxo máximo pode ser visto como um caso especial de problemas de fluxo de rede mais complexos, como o problema de circulação . O valor máximo de um st flow (ou seja, fluxo da fonte s para o sumidouro t) é igual à capacidade mínima de um st corte (ou seja, corte separando s de t) na rede, conforme declarado no max-flow min- teorema de corte .

História

O problema de fluxo máximo foi formulado pela primeira vez em 1954 por TE Harris e FS Ross como um modelo simplificado do fluxo de tráfego ferroviário soviético.

Em 1955, Lester R. Ford, Jr. e Delbert R. Fulkerson criaram o primeiro algoritmo conhecido, o algoritmo Ford-Fulkerson . Em seu artigo de 1955, Ford e Fulkerson escreveram que o problema de Harris e Ross é formulado da seguinte forma (ver p. 5):

Considere uma rede ferroviária conectando duas cidades por meio de várias cidades intermediárias, onde cada link da rede possui um número atribuído a ela que representa sua capacidade. Assumindo uma condição de estado estacionário, encontre um fluxo máximo de uma determinada cidade para a outra.

Em seu livro Flows in Network , em 1962, Ford e Fulkerson escreveram:

Foi proposto aos autores na primavera de 1955 por TE Harris, que, em conjunto com o General FS Ross (aposentado), formulou um modelo simplificado de fluxo de tráfego ferroviário e apontou este problema particular como o problema central sugerido pelo modelo [11].

onde [11] se refere ao relatório secreto de 1955, Fundamentos de um Método para Avaliar Capacidades da Rede Ferroviária, de Harris e Ross (ver pág. 5).

Ao longo dos anos, várias soluções aprimoradas para o problema de fluxo máximo foram descobertas, notavelmente o algoritmo de caminho de aumento mais curto de Edmonds e Karp e, independentemente, Dinitz; o algoritmo de bloqueio de fluxo de Dinitz; o algoritmo push-relabel de Goldberg e Tarjan ; e o algoritmo de fluxo de bloqueio binário de Goldberg e Rao. Os algoritmos de Sherman e Kelner, Lee, Orecchia e Sidford, respectivamente, encontram um fluxo máximo aproximadamente ótimo, mas funcionam apenas em gráficos não direcionados.

Em 2013, James B. Orlin publicou um artigo descrevendo um algoritmo. ${\ displaystyle O (| V || E |)}$

Definição

A rede de fluxo, com fonte s e pia t . Os números próximos à borda são as capacidades.

Primeiro, estabelecemos algumas notações:

• Deixe ser uma rede sendo a fonte e o coletor de, respectivamente.${\ displaystyle N = (V, E)}$${\ displaystyle s, t \ in V}$${\ displaystyle N}$
• Se é função nas bordas de, então seu valor em é denotado por ou${\ displaystyle g}$${\ displaystyle N}$${\ displaystyle (u, v) \ in E}$${\ displaystyle g_ {uv}}$${\ displaystyle g (u, v).}$

Definição. A capacidade de uma borda é a quantidade máxima de fluxo que pode passar por uma borda. Formalmente é um mapa${\ displaystyle c: E \ to \ mathbb {R} ^ {+}.}$

Definição. Um fluxo é um mapa que satisfaz o seguinte: ${\ displaystyle f: E \ to \ mathbb {R}}$

• Restrição de capacidade . O fluxo de uma borda não pode ultrapassar sua capacidade, ou seja: para todos${\ displaystyle f_ {uv} \ leq c_ {uv}}$${\ displaystyle (u, v) \ in E.}$
• Conservação de fluxos. A soma dos fluxos que entram em um nó deve ser igual à soma dos fluxos que saem desse nó, exceto para a origem e o sumidouro. Ou:

${\ displaystyle \ forall v \ in V \ setminus \ {s, t \}: \ quad \ sum _ {u: (u, v) \ in E} f_ {uv} = \ sum _ {u: (v, u) \ em E} f_ {vu}.}$

Observação . Os fluxos são assimétricos: para todos${\ displaystyle f_ {uv} = - f_ {vu}}$${\ displaystyle (u, v) \ in E.}$

Definição. O valor do fluxo é a quantidade de fluxo que passa da fonte para o sumidouro. Formalmente, para um fluxo , é dado por: ${\ displaystyle f: E \ to \ mathbb {R} ^ {+}}$

${\ displaystyle | f | = \ sum _ {v: (s, v) \ in E} f_ {sv}.}$

Definição. O problema do fluxo máximo é direcionar o máximo de fluxo possível da fonte ao coletor, ou seja, encontrar o fluxo com valor máximo. ${\ displaystyle f _ {\ textrm {max}}}$

Observe que vários fluxos máximos podem existir, e se valores reais arbitrários (ou mesmo racionais arbitrários) de fluxo são permitidos (em vez de apenas inteiros), há exatamente um fluxo máximo, ou infinitamente muitos, uma vez que existem infinitas combinações lineares de os fluxos máximos de base. Em outras palavras, se enviarmos unidades de fluxo na borda em um fluxo máximo, e unidades de fluxo em outro fluxo máximo, então, para cada um , podemos enviar unidades e direcionar o fluxo nas bordas restantes de acordo, para obter outro fluxo máximo. Se os valores de fluxo podem ser quaisquer números reais ou racionais, então existem infinitos desses valores para cada par . ${\ displaystyle x}$${\ displaystyle u}$${\ displaystyle y> x}$${\ displaystyle u}$${\ displaystyle \ Delta \ in [0, yx]}$${\ displaystyle x + \ Delta}$${\ displaystyle u}$${\ displaystyle \ Delta}$${\ displaystyle x, y}$

Algoritmos

A tabela a seguir lista algoritmos para resolver o problema de fluxo máximo.

Método	Complexidade	Descrição
Programação linear		Restrições dadas pela definição de um fluxo legal . Veja o programa linear aqui.
Algoritmo Ford-Fulkerson	${\ displaystyle O (E \ vert f_ {max} \ vert)}$	Enquanto houver um caminho aberto no gráfico residual, envie o mínimo das capacidades residuais no caminho. O algoritmo só tem garantia de término se todos os pesos forem racionais , caso em que a quantidade adicionada ao fluxo em cada etapa é pelo menos o maior divisor comum dos pesos. Caso contrário, é possível que o algoritmo não convirja para o valor máximo. No entanto, se o algoritmo terminar, é garantido encontrar o valor máximo.
Algoritmo Edmonds-Karp	${\ displaystyle O (VE ^ {2})}$	Uma especialização de Ford – Fulkerson, encontrando caminhos ampliadores com pesquisa abrangente .
Algoritmo de Dinic	${\ displaystyle O (V ^ {2} E)}$	Em cada fase, os algoritmos constroem um gráfico em camadas com pesquisa em largura no gráfico residual . O fluxo máximo em um gráfico em camadas pode ser calculado com o tempo, e o número máximo de fases é . Em redes com capacidades unitárias, o algoritmo de Dinic termina no tempo. ${\ displaystyle O (VE)}$${\ displaystyle V-1}$${\ displaystyle O (\ min \ {V ^ {2/3}, E ^ {1/2} \} E)}$
Algoritmo MKM (Malhotra, Kumar, Maheshwari)	${\ displaystyle O (V ^ {3})}$	Uma modificação do algoritmo de Dinic com uma abordagem diferente para construir fluxos de bloqueio. Consulte o papel original .
Algoritmo de Dinic com árvores dinâmicas	${\ displaystyle O (VE \ log V)}$	A estrutura de dados de árvores dinâmicas acelera o cálculo de fluxo máximo no gráfico em camadas para . ${\ displaystyle O (VE \ log V)}$
Algoritmo push-relabel geral	${\ displaystyle O (V ^ {2} E)}$	O algoritmo push relabel mantém um pré-fluxo, ou seja, uma função de fluxo com possibilidade de excesso nos vértices. O algoritmo é executado enquanto houver um vértice com excesso positivo, ou seja, um vértice ativo no gráfico. A operação push aumenta o fluxo em uma borda residual e uma função de altura nos vértices controla através da qual as bordas residuais podem ser empurradas. A função de altura é alterada pela operação de reclassificação. As definições adequadas dessas operações garantem que a função de fluxo resultante seja um fluxo máximo.
Algoritmo push-relabel com regra de seleção de vértice FIFO	${\ displaystyle O (V ^ {3})}$	Variante do algoritmo push-relabel que sempre seleciona o vértice ativo mais recentemente e executa operações push enquanto o excesso é positivo e há arestas residuais admissíveis deste vértice.
Algoritmo push-relabel com regra de seleção de vértice de distância máxima	${\ displaystyle O (V ^ {2} {\ sqrt {E}})}$	Variante do algoritmo push-relabel que sempre seleciona o vértice mais distante de ou ( ou seja, o vértice de rótulo mais alto), mas de outra forma continua como o algoritmo FIFO. ${\ displaystyle s}$${\ displaystyle t}$
Algoritmo push-relabel com árvores dinâmicas	${\ displaystyle O \ left (VE \ log {\ frac {V ^ {2}} {E}} \ right)}$	O algoritmo constrói árvores de tamanho limitado no gráfico residual em relação à função altura. Essas árvores fornecem operações de push multinível, ou seja, empurrar ao longo de um caminho de saturação inteiro em vez de uma única aresta.
Algoritmo de KRT (King, Rao, Tarjan)	${\ displaystyle O \ left (VE \ log _ {\ frac {E} {V \ log V}} V \ right)}$
Algoritmo de fluxo de bloqueio binário	${\ displaystyle O \ left (E \ cdot \ min \ {V ^ {2/3}, E ^ {1/2} \} \ cdot \ log {\ frac {V ^ {2}} {E}} \ cdot \ log U \ right)}$	O valor U corresponde à capacidade máxima da rede.
Algoritmo de James B Orlin + KRT (King, Rao, Tarjan)	${\ displaystyle O (VE)}$	Resolve o algoritmo do Orlin max-fluir em tempo para enquanto KRT resolve-lo em para . ${\ displaystyle O (VE)}$${\ displaystyle E \ leq O (V ^ {{\ frac {16} {15}} - \ epsilon})}$${\ displaystyle O (VE)}$${\ displaystyle E> V ^ {1+ \ epsilon}}$
Algoritmo Kathuria-Liu-Sidford	${\ displaystyle E ^ {4/3 + o (1)} U ^ {1/3}}$	Métodos de ponto interno e aumento de borda usando fluxos -norm. Baseia-se no algoritmo anterior de Madry, que alcançou o tempo de execução . ${\ displaystyle \ ell _ {p}}$${\ displaystyle {\ tilde {O}} (E ^ {10/7} U ^ {1/7})}$
Algoritmo BLNPSSSW / BLLSSSW	${\ displaystyle {\ tilde {O}} ((E + V ^ {3/2}) \ log U)}$	Métodos de pontos interiores e manutenção dinâmica de fluxos elétricos com decomposições expansoras.
Algoritmo Gao-Liu-Peng	${\ displaystyle {\ tilde {O}} (E ^ {{\ frac {3} {2}} - {\ frac {1} {328}}} \ log U)}$	O algoritmo de Gao, Liu e Peng gira em torno de manter dinamicamente os fluxos elétricos crescentes no núcleo do algoritmo baseado no método do ponto interior de [Mądry JACM '16]. Isso envolve o projeto de estruturas de dados que, em configurações limitadas, retornam bordas com grande energia elétrica em um gráfico submetido a atualizações de resistência.

Para algoritmos adicionais, consulte Goldberg & Tarjan (1988) .

Teorema do fluxo integral

O teorema do fluxo integral afirma que

Se cada borda em uma rede de fluxo tem capacidade integral, então existe um fluxo máximo integral.

A alegação não é apenas que o valor do fluxo é um número inteiro, que segue diretamente do teorema de corte mínimo do fluxo máximo , mas que o fluxo em cada aresta é integral. Isso é crucial para muitas aplicações combinatórias (veja abaixo), onde o fluxo através de uma borda pode codificar se o item correspondente a essa borda deve ser incluído no conjunto procurado ou não.

Aplicativo

Problema de fluxo máximo de múltiplos sumidouros de fontes múltiplas

Fig. 4.1.1. Transformação de um problema de fluxo máximo de múltiplos sumidouros de fontes múltiplas em um problema de fluxo máximo de sumidouro único de fonte única

Dada uma rede com um conjunto de fontes e um conjunto de sumidouros em vez de apenas uma fonte e um sumidouro, devemos encontrar o fluxo máximo . Podemos transformar o problema de múltiplos sumidouros de múltiplas fontes em um problema de fluxo máximo, adicionando uma fonte consolidada conectada a cada vértice em e um sumidouro consolidado conectado por cada vértice em (também conhecido como supersource e supersink ) com capacidade infinita em cada aresta ( Consulte a Fig. 4.1.1.). ${\ displaystyle N = (V, E)}$${\ displaystyle S = \ {s_ {1}, \ ldots, s_ {n} \}}$${\ displaystyle T = \ {t_ {1}, \ ldots, t_ {m} \}}$${\ displaystyle N}$${\ displaystyle S}$${\ displaystyle T}$

Correspondência bipartida de cardinalidade máxima

Fig. 4.3.1. Transformação de um problema de correspondência bipartida máxima em um problema de fluxo máximo

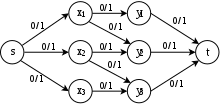
Dado um grafo bipartido , devemos encontrar uma correspondência de cardinalidade máxima em , que é uma correspondência que contém o maior número possível de arestas. Este problema pode ser transformado em um problema de fluxo máximo através da construção de uma rede , onde ${\ displaystyle G = (X \ xícara Y, E)}$${\ displaystyle G}$${\ displaystyle N = (X \ xícara Y \ xícara \ {s, t \}, E ')}$

1. ${\ displaystyle E '}$contém as arestas direcionadas de para .${\ displaystyle G}$${\ displaystyle X}$${\ displaystyle Y}$
2. ${\ displaystyle (s, x) \ in E '}$para cada um e para cada um .${\ displaystyle x \ in X}$${\ displaystyle (y, t) \ in E '}$${\ displaystyle y \ in Y}$
3. ${\ displaystyle c (e) = 1}$para cada um (Ver Fig. 4.3.1).${\ displaystyle e \ in E '}$

Então, o valor do fluxo máximo em é igual ao tamanho da correspondência máxima em , e uma correspondência de cardinalidade máxima pode ser encontrada tomando as arestas que têm fluxo em um fluxo máximo integral. ${\ displaystyle N}$${\ displaystyle G}$${\ displaystyle 1}$

Cobertura mínima do caminho no gráfico acíclico direcionado

Dado um grafo acíclico direcionado , devemos encontrar o número mínimo de caminhos disjuntos de vértices para cobrir cada vértice em . Podemos construir um grafo bipartido a partir de , onde ${\ displaystyle G = (V, E)}$${\ displaystyle V}$${\ displaystyle G '= (V _ {\ textrm {out}} \ cup V _ {\ textrm {in}}, E')}$${\ displaystyle G}$

1. ${\ displaystyle V _ {\ textrm {saída}} = \ {v _ {\ textrm {saída}} \ mid v \ in V \ land v {\ text {tem borda (s) de saída}} \}}$
2. ${\ displaystyle V _ {\ textrm {in}} = \ {v _ {\ textrm {in}} \ mid v \ in V \ land v {\ text {tem borda (s) de entrada}} \}}$
3. ${\ displaystyle E '= \ {(u _ {\ textrm {out}}, v _ {\ textrm {in}}) \ in V_ {out} \ times V_ {in} \ mid (u, v) \ in E \ }}$.

Em seguida, pode ser mostrado que tem uma correspondência de tamanho se e somente se tem uma cobertura de caminho de vértice disjunta contendo arestas e caminhos, onde é o número de vértices em . Portanto, o problema pode ser resolvido encontrando a correspondência de cardinalidade máxima em . ${\ displaystyle G '}$${\ displaystyle M}$${\ displaystyle m}$${\ displaystyle G}$${\ displaystyle C}$${\ displaystyle m}$${\ displaystyle nm}$${\ displaystyle n}$${\ displaystyle G}$${\ displaystyle G '}$

Intuitivamente, se dois vértices forem correspondidos , a aresta estará contida em . Claramente, o número de arestas em é . Para ver que é disjunta de vértice, considere o seguinte: ${\ displaystyle u _ {\ mathrm {out}}, v _ {\ mathrm {in}}}$${\ displaystyle M}$${\ displaystyle (u, v)}$${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle m}$${\ displaystyle C}$

1. Cada vértice no pode ser não-correspondida em , caso em que não existem arestas deixando em ; ou ele pode ser combinado , caso em que não é exatamente uma borda deixando em . Em qualquer caso, não mais do que uma aresta deixa qualquer vértice dentro .${\ displaystyle v _ {\ textrm {out}}}$${\ displaystyle G '}$${\ displaystyle M}$${\ displaystyle v}$${\ displaystyle C}$${\ displaystyle v}$${\ displaystyle C}$${\ displaystyle v}$${\ displaystyle C}$
2. Da mesma forma, para cada vértice em - se houver correspondência, há uma única aresta de entrada em ; caso contrário , não tem bordas de entrada .${\ displaystyle v _ {\ textrm {in}}}$${\ displaystyle G '}$${\ displaystyle v}$${\ displaystyle C}$${\ displaystyle v}$${\ displaystyle C}$

Portanto, nenhum vértice tem duas arestas de entrada ou duas de saída , o que significa que todos os caminhos de entrada são separados por vértice. ${\ displaystyle C}$${\ displaystyle C}$

Para mostrar que a capa tem tamanho , começamos com uma capa vazia e a construímos de forma incremental. Para adicionar um vértice à cobertura, podemos adicioná-lo a um caminho existente ou criar um novo caminho de comprimento zero começando nesse vértice. O primeiro caso é aplicável sempre que um e algum caminho na capa começa em , ou e algum caminho termina em . O último caso é sempre aplicável. No primeiro caso, o número total de arestas na tampa é aumentado em 1 e o número de caminhos permanece o mesmo; no último caso, o número de caminhos é aumentado e o número de arestas permanece o mesmo. Agora está claro que depois de cobrir todos os vértices, a soma do número de caminhos e arestas na capa é . Portanto, se o número de arestas na capa for , o número de caminhos será . ${\ displaystyle C}$${\ displaystyle nm}$${\ displaystyle u}$${\ displaystyle (u, v) \ in E}$${\ displaystyle v}$${\ displaystyle (v, u) \ in E}$${\ displaystyle v}$${\ displaystyle n}$${\ displaystyle n}$${\ displaystyle m}$${\ displaystyle nm}$

Fluxo máximo com capacidades de vértice

Fig. 4.4.1. Transformação de um problema de fluxo máximo com restrição de capacidades de vértice no problema de fluxo máximo original por divisão de nó

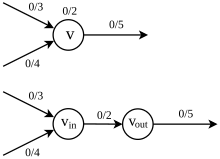
Deixe ser uma rede. Suponha que haja capacidade em cada nó além da capacidade da borda, ou seja, um mapeamento tal que o fluxo deve satisfazer não apenas a restrição de capacidade e a conservação dos fluxos, mas também a restrição de capacidade do vértice ${\ displaystyle N = (V, E)}$${\ displaystyle c: V \ to \ mathbb {R} ^ {+},}$${\ displaystyle f}$

${\ displaystyle \ sum _ {i \ in V} f_ {iv} \ leq c (v) \ qquad \ forall v \ in V \ barra invertida \ {s, t \}.}$

Em outras palavras, a quantidade de fluxo que passa por um vértice não pode exceder sua capacidade. Para encontrar o fluxo máximo transversal , podemos transformar o problema no problema de fluxo máximo no sentido original, expandindo . Primeiro, cada um é substituído por e , onde é conectado pelas bordas que entram e são conectadas às bordas que saem , então atribua capacidade para a borda que conecta e (ver Fig. 4.4.1). Nessa rede expandida, a restrição de capacidade do vértice é removida e, portanto, o problema pode ser tratado como o problema de fluxo máximo original. ${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle v \ in V}$${\ displaystyle v _ {\ text {in}}}$${\ displaystyle v _ {\ text {out}}}$${\ displaystyle v _ {\ text {in}}}$${\ displaystyle v}$${\ displaystyle v _ {\ text {out}}}$${\ displaystyle v}$${\ displaystyle c (v)}$${\ displaystyle v _ {\ text {in}}}$${\ displaystyle v _ {\ text {out}}}$

Número máximo de caminhos de s a t

Dado um grafo direcionado e dois vértices e , devemos encontrar o número máximo de caminhos de a . Este problema tem várias variantes: ${\ displaystyle G = (V, E)}$${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle s}$${\ displaystyle t}$

1. Os caminhos devem ser desconexos. Esse problema pode ser transformado em um problema de fluxo máximo construindo uma rede de , com e sendo a fonte e o sumidouro de , respectivamente, e atribuindo a cada aresta uma capacidade de . Nesta rede, o fluxo máximo é se houver caminhos disjuntos de borda. ${\ displaystyle N = (V, E)}$${\ displaystyle G}$${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle N}$${\ displaystyle 1}$${\ displaystyle k}$${\ displaystyle k}$

2. Os caminhos devem ser independentes, ou seja, separados por vértice (exceto para e ). Podemos construir uma rede de com capacidade de vértice, onde as capacidades de todos os vértices e todas as arestas são . Então, o valor do fluxo máximo é igual ao número máximo de caminhos independentes de a . ${\ displaystyle s}$${\ displaystyle t}$${\ displaystyle N = (V, E)}$${\ displaystyle G}$${\ displaystyle 1}$${\ displaystyle s}$${\ displaystyle t}$

3. Além dos caminhos serem desconexos de aresta e / ou desconexão de vértice, os caminhos também têm uma restrição de comprimento: contamos apenas caminhos cujo comprimento é exatamente , ou no máximo . A maioria das variantes desse problema são NP-completas, exceto para pequenos valores de . ${\ displaystyle k}$${\ displaystyle k}$${\ displaystyle k}$

Problema de fechamento

Um fecho de um grafo orientado é um conjunto de vértices C , de tal modo que não há bordas deixar C . O problema de fechamento é a tarefa de encontrar o fechamento de peso máximo ou mínimo em um gráfico direcionado ponderado por vértice. Pode ser resolvido em tempo polinomial usando uma redução ao problema de fluxo máximo.

Aplicativos do mundo real

Eliminação de beisebol

Construção de fluxo de rede para problema de eliminação de beisebol

No problema de eliminação do beisebol, há n equipes competindo em uma liga. Em um estágio específico da temporada da liga, w _i é o número de vitórias er _i é o número de jogos restantes para as equipes i e r _ij é o número de jogos restantes contra a equipe j . Uma equipe é eliminada se não tiver chance de terminar a temporada em primeiro lugar. A tarefa do problema de eliminação do beisebol é determinar quais times são eliminados em cada ponto durante a temporada. Schwartz propôs um método que reduz esse problema ao fluxo máximo da rede. Neste método, uma rede é criada para determinar se a equipe k é eliminada.

Seja G = ( V , E ) uma rede com s , t ∈ V sendo a fonte e o sumidouro, respectivamente. Adiciona-se um nó de jogo _ij - que representa o número de jogadas entre essas duas equipes. Nós também adicionar um nó equipe para cada equipe e conectar cada nó jogo { i , j } com i < j a V , e conecta cada um deles de s por uma aresta com capacidade r _ij - que representa o número de jogos entre estes dois equipes. Também adicionamos um nó de equipe para cada equipe e conectamos cada nó de jogo { i , j } com dois nós de equipe i e j para garantir que um deles vença. Não é necessário restringir o valor do fluxo nessas bordas. Finalmente, as arestas são feitas do nó da equipe i para o nó sorvedouro t e a capacidade de w _k + r _k - w _i é definida para evitar que a equipe i ganhe mais do que w _k + r _k . Seja S o conjunto de todas as equipes participantes da liga e deixe

${\ displaystyle r (S - \ {k \}) = \ sum _ {i, j \ in \ {S - \ {k \} \} \ sobre i <j} r_ {ij}}$.

Neste método, diz-se equipa k não é eliminada se e só se um valor de fluxo de tamanho r ( S - { k }) existe na rede G . No artigo mencionado é provado que este valor de fluxo é o valor máximo de fluxo de s para t .

Agendamento da companhia aérea

No setor de aviação civil, um grande problema é a programação das tripulações de vôo. O problema de programação de companhias aéreas pode ser considerado como uma aplicação de fluxo máximo de rede estendido. A entrada deste problema é um conjunto de voos F que contém as informações sobre onde e quando cada voo sai e chega. Em uma versão da programação da companhia aérea, o objetivo é produzir uma programação viável com no máximo k tripulações.

Para resolver este problema, usa-se uma variação do problema de circulação chamada circulação limitada, que é a generalização dos problemas de fluxo de rede , com a restrição adicional de um limite inferior nos fluxos de borda.

Seja G = ( V , E ) uma rede com s , t ∈ V como nós fonte e sorvedouro. Para a origem e o destino de cada voo i , adiciona-se dois nós a V , o nó s _i como a origem e o nó d _i como o nó de destino do voo i . Também se adiciona as seguintes arestas a E :

1. Uma borda com capacidade [0, 1] entre s e cada um s _i .
2. Uma aresta com capacidade [0, 1] entre cada d _i e t .
3. Uma aresta com capacidade [1, 1] entre cada par de s _i e d _i .
4. Uma aresta com capacidade [0, 1] entre cada d _i e s _j , se a fonte s _j for alcançável com uma quantidade razoável de tempo e custo a partir do destino do vôo i .
5. Uma aresta com capacidade [0, ∞ ] entre s e t .

No método mencionado, é afirmado e provado que encontrar um valor de fluxo de k em G entre s e t é igual a encontrar um horário viável para o conjunto de vôo F com no máximo k tripulações.

Outra versão da programação da companhia aérea é encontrar as tripulações mínimas necessárias para realizar todos os voos. A fim de encontrar uma solução para este problema, um gráfico bipartido L' = ( A ∪ B , E ) é criado onde cada voo tem uma cópia em conjunto Um e conjunto B . Se o mesmo plano pode realizar voo j depois de voo i , i ∈ A está ligado ao j ∈ B . Uma correspondência em G ' induz uma programação para F e, obviamente, a correspondência bipartida máxima neste gráfico produz uma programação de linha aérea com um número mínimo de tripulações. Como é mencionado na parte de Aplicação deste artigo, a correspondência bipartida de cardinalidade máxima é uma aplicação do problema de fluxo máximo.

Problema de demanda de circulação

Existem algumas fábricas que produzem mercadorias e algumas aldeias onde as mercadorias devem ser entregues. Eles são conectados por uma rede de estradas com cada estrada tendo uma capacidade c para o máximo de mercadorias que podem fluir por ela. O problema é saber se existe uma circulação que atenda a demanda. Esse problema pode ser transformado em um problema de fluxo máximo.

1. Adicione um nó de origem s e adicione arestas a partir dele para cada nó de fábrica f _i com capacidade p _i, onde p _i é a taxa de produção da fábrica f _i .
2. Adicione um nó sumidouro t e adicione arestas de todas as aldeias v _i a t com capacidade d _i onde d _i é a taxa de demanda da aldeia v _i .

Seja G = ( V , E ) esta nova rede. Existe uma circulação que satisfaz a demanda se e somente se:

Valor de fluxo máximo ( G ) .${\ displaystyle = \ sum _ {i \ in v} d_ {i}}$

Se existe uma circulação, olhar para a solução de fluxo máximo daria a resposta quanto à quantidade de bens que devem ser enviados em uma estrada particular para satisfazer as demandas.

O problema pode ser estendido adicionando-se um limite inferior ao fluxo em algumas bordas.

Segmentação de imagem

Imagem original de tamanho 8x8.

Rede construída a partir do bitmap. A fonte está à esquerda, a pia à direita. Quanto mais escura for uma borda, maior será sua capacidade. a _i é alto quando o pixel é verde, b _i quando o pixel não é verde. As penalidades p _ij são todas iguais.

Em seu livro, Kleinberg e Tardos apresentam um algoritmo para segmentar uma imagem. Eles apresentam um algoritmo para encontrar o fundo e o primeiro plano em uma imagem. Mais precisamente, o algoritmo toma um bitmap como uma entrada modelada da seguinte forma: a _i ≥ 0 é a probabilidade de que o pixel i pertença ao primeiro plano, b _i ≥ 0 a probabilidade de que o pixel i pertença ao plano de fundo, e p _ij é o penalidade se dois pixels adjacentes i e j forem colocados um no primeiro plano e o outro no plano de fundo. O objetivo é encontrar uma partição ( A , B ) do conjunto de pixels que maximize a seguinte quantidade

${\ displaystyle q (A, B) = \ sum _ {i \ in A} a_ {i} + \ sum _ {i \ in B} b_ {i} - \ sum _ {\ begin {matriz} i, j {\ text {adjacente}} \\ | A \ cap \ {i, j \} | = 1 \ end {matriz}} p_ {ij}}$,

De fato, para pixels em A (considerados como o primeiro plano), ganhamos a _i ; para todos os pixels em B (considerados como fundo), ganhamos b _i . Na borda, entre dois pixels adjacentes i e j , perdemos p _ij . É equivalente a minimizar a quantidade

${\ displaystyle q '(A, B) = \ sum _ {i \ in A} b_ {i} + \ sum _ {i \ in B} a_ {i} + \ sum _ {\ begin {matriz} i, j {\ text {adjacente}} \\ | A \ cap \ {i, j \} | = 1 \ end {matriz}} p_ {ij}}$

Porque

${\ displaystyle q (A, B) = \ sum _ {i \ in A \ cup B} a_ {i} + \ sum _ {i \ in A \ cup B} b_ {i} -q '(A, B ).}$

Corte mínimo exibido na rede (triângulos VS círculos).

Agora construímos a rede cujos nós são o pixel, mais uma fonte e um coletor, consulte a Figura à direita. Conectamos a fonte ao pixel i por uma aresta de peso a _i . Conectamos o pixel i à pia por uma aresta de peso b _i . Conectamos o pixel i ao pixel j com peso p _ij . Agora, resta calcular um corte mínimo nessa rede (ou, de forma equivalente, um fluxo máximo). A última figura mostra um corte mínimo.

Extensões

1. No problema de fluxo de custo mínimo , cada aresta ( u , v) também tem um coeficiente de custo a _uv além de sua capacidade. Se o fluxo através da borda é f _uv , em seguida, o custo total é uma _uv f _UV . É necessário encontrar um fluxo de determinado tamanho d , com o menor custo. Na maioria das variantes, os coeficientes de custo podem ser positivos ou negativos. Existem vários algoritmos de tempo polinomial para esse problema.

2. O problema de fluxo máximo pode ser aumentado por restrições disjuntivas : uma restrição disjuntiva negativa diz que um certo par de arestas não pode ter simultaneamente um fluxo diferente de zero; uma restrição disjuntiva positiva diz que, em um determinado par de arestas, pelo menos um deve ter um fluxo diferente de zero. Com restrições negativas, o problema se torna fortemente NP-difícil, mesmo para redes simples. Com restrições positivas, o problema é polinomial se fluxos fracionários forem permitidos, mas pode ser fortemente NP-difícil quando os fluxos devem ser integrais.

Referências

Leitura adicional

• Joseph Cheriyan e Kurt Mehlhorn (1999). "Uma análise da regra de seleção de nível mais alto no algoritmo de fluxo máximo de pré-fluxo". Cartas de processamento de informações . 69 (5): 239–242. CiteSeerX  10.1.1.42.8563 . doi : 10.1016 / S0020-0190 (99) 00019-8 .
• Daniel D. Sleator e Robert E. Tarjan (1983). "Uma estrutura de dados para árvores dinâmicas" (PDF) . Journal of Computer and System Sciences . 26 (3): 362–391. doi : 10.1016 / 0022-0000 (83) 90006-5 . ISSN  0022-0000 .
• Eugene Lawler (2001). "4. Fluxos de rede". Otimização Combinatória: Redes e Matroids . Dover. pp. 109–177. ISBN 978-0-486-41453-9.