Círculo de Mohr - Mohr's circle

Figura 1. Círculos de Mohr para um estado tridimensional de tensão

O círculo de Mohr é uma representação gráfica bidimensional da lei de transformação do tensor de tensão de Cauchy .

O círculo de Mohr é frequentemente usado em cálculos relacionados à engenharia mecânica para resistência de materiais , engenharia geotécnica para resistência de solos e engenharia estrutural para resistência de estruturas construídas. Também é usado para calcular tensões em muitos planos, reduzindo-as a componentes verticais e horizontais. Eles são chamados de planos principais, nos quais as tensões principais são calculadas; O círculo de Mohr também pode ser usado para encontrar os planos principais e as tensões principais em uma representação gráfica e é uma das maneiras mais fáceis de fazer isso.

Depois de realizar uma análise de tensão em um corpo material assumido como um contínuo , os componentes do tensor de tensão de Cauchy em um ponto de material específico são conhecidos em relação a um sistema de coordenadas . O círculo de Mohr é então usado para determinar graficamente os componentes de tensão agindo em um sistema de coordenadas girado, ou seja, agindo em um plano orientado de forma diferente passando por aquele ponto.

A abscissa e ordenada ( , ) de cada ponto do círculo são as magnitudes das componentes da tensão normal e da tensão de cisalhamento , respectivamente, atuando no sistema de coordenadas girado. Em outras palavras, o círculo é o local dos pontos que representam o estado de tensão em planos individuais em todas as suas orientações, onde os eixos representam os eixos principais do elemento de tensão. ${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$

O engenheiro alemão do século 19, Karl Culmann, foi o primeiro a conceber uma representação gráfica para tensões enquanto considerava tensões longitudinais e verticais em vigas horizontais durante a flexão . Seu trabalho inspirou o colega engenheiro alemão Christian Otto Mohr (homônimo do círculo), que o estendeu para tensões bidimensionais e tridimensionais e desenvolveu um critério de falha baseado no círculo de tensões.

Métodos gráficos alternativos para a representação do estado de tensão em um ponto incluem o elipsóide de tensão de Lamé e a quádrica de tensão de Cauchy .

O círculo de Mohr pode ser aplicado a qualquer matriz de tensor 2x2 simétrica , incluindo a deformação e o momento dos tensores de inércia .

Motivação

Figura 2. Tensão em um corpo de material deformável carregado assumido como um continuum.

As forças internas são produzidas entre as partículas de um objeto deformável, assumido como um continuum , como uma reação às forças externas aplicadas, ou seja, forças de superfície ou forças de corpo . Essa reação segue as leis de movimento de Euler para um contínuo, que são equivalentes às leis de movimento de Newton para uma partícula. Uma medida da intensidade dessas forças internas é chamada de estresse . Como o objeto é assumido como um continuum, essas forças internas são distribuídas continuamente dentro do volume do objeto.

Em engenharia, por exemplo, estrutural , mecânica ou geotécnica , a distribuição de tensões dentro de um objeto, por exemplo tensões em uma massa rochosa ao redor de um túnel, asas de avião ou colunas de edifícios, é determinada por meio de uma análise de tensão . O cálculo da distribuição de tensões implica na determinação de tensões em cada ponto (partícula material) do objeto. De acordo com Cauchy , a tensão em qualquer ponto num objecto (Figura 2), assume-se como um processo contínuo, é completamente definido pelos componentes nove de stress de uma segunda ordem tensor de tipo (2,0) conhecido como o tensor de Cauchy , : ${\ displaystyle \ sigma _ {ij}}$${\ displaystyle {\ boldsymbol {\ sigma}}}$

${\ displaystyle {\ boldsymbol {\ sigma}} = \ left [{\ begin {matrix} \ sigma _ {11} & \ sigma _ {12} & \ sigma _ {13} \\\ sigma _ {21} & \ sigma _ {22} & \ sigma _ {23} \\\ sigma _ {31} & \ sigma _ {32} & \ sigma _ {33} \\\ end {matriz}} \ direita] \ equiv \ esquerda [{\ begin {matrix} \ sigma _ {xx} & \ sigma _ {xy} & \ sigma _ {xz} \\\ sigma _ {yx} & \ sigma _ {yy} & \ sigma _ {yz} \ \\ sigma _ {zx} & \ sigma _ {zy} & \ sigma _ {zz} \\\ end {matriz}} \ direita] \ equiv \ left [{\ begin {matriz} \ sigma _ {x} & \ tau _ {xy} & \ tau _ {xz} \\\ tau _ {yx} & \ sigma _ {y} & \ tau _ {yz} \\\ tau _ {zx} & \ tau _ {zy} & \ sigma _ {z} \\\ end {matriz}} \ direita]}$

Figura 3. Transformação de tensão em um ponto em um contínuo sob condições de tensão plana.

Depois que a distribuição de tensões dentro do objeto foi determinada com respeito a um sistema de coordenadas , pode ser necessário calcular os componentes do tensor de tensão em um ponto de material particular com respeito a um sistema de coordenadas girado , ou seja, as tensões atuando em um plano com uma orientação diferente passando por aquele ponto de interesse - formando um ângulo com o sistema de coordenadas (Figura 3). Por exemplo, é interessante encontrar a tensão normal máxima e a tensão de cisalhamento máxima, bem como a orientação dos planos sobre os quais atuam. Para isso, é necessário realizar uma transformação tensorial sob uma rotação do sistema de coordenadas. A partir da definição de tensor , o tensor de tensão de Cauchy obedece à lei de transformação do tensor . Uma representação gráfica dessa lei de transformação para o tensor de tensão de Cauchy é o círculo de Mohr para a tensão. ${\ displaystyle (x, y)}$${\ displaystyle P}$${\ displaystyle (x ', y')}$${\ displaystyle (x, y)}$

Círculo de Mohr para o estado bidimensional de tensão

Figura 4. Componentes de tensão em um plano que passa por um ponto em um contínuo sob condições de tensão plana.

Em duas dimensões, o tensor de tensão em um determinado ponto do material em relação a quaisquer duas direções perpendiculares é completamente definido por apenas três componentes de tensão. Para o sistema de coordenadas específico, esses componentes de tensão são: as tensões normais e , e a tensão de cisalhamento . A partir do balanço do momento angular, a simetria do tensor de tensão de Cauchy pode ser demonstrada. Essa simetria implica isso . Assim, o tensor de tensão de Cauchy pode ser escrito como: ${\ displaystyle P}$${\ displaystyle (x, y)}$${\ displaystyle \ sigma _ {x}}$${\ displaystyle \ sigma _ {y}}$${\ displaystyle \ tau _ {xy}}$${\ displaystyle \ tau _ {xy} = \ tau _ {yx}}$

${\ displaystyle {\ boldsymbol {\ sigma}} = \ left [{\ begin {matrix} \ sigma _ {x} & \ tau _ {xy} & 0 \\\ tau _ {xy} & \ sigma _ {y} & 0 \\ 0 & 0 & 0 \\\ end {matriz}} \ right] \ equiv \ left [{\ begin {matrix} \ sigma _ {x} & \ tau _ {xy} \\\ tau _ {xy} & \ sigma _ {y} \\\ end {matrix}} \ right]}$

O objetivo é usar o círculo de Mohr para encontrar os componentes de tensão e em um sistema de coordenadas girado , ou seja, em um plano orientado diferentemente passando e perpendicular ao plano - (Figura 4). O sistema de coordenadas girado faz um ângulo com o sistema de coordenadas original . ${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle (x ', y')}$${\ displaystyle P}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle (x ', y')}$${\ displaystyle \ theta}$${\ displaystyle (x, y)}$

Equação do círculo de Mohr

Para derivar a equação do círculo de Mohr para os casos bidimensionais de tensão plana e deformação plana , primeiro considere um elemento de material infinitesimal bidimensional em torno de um ponto de material (Figura 4), com uma área unitária na direção paralela ao - plano, ou seja, perpendicular à página ou tela. ${\ displaystyle P}$${\ displaystyle y}$${\ displaystyle z}$

A partir do equilíbrio de forças no elemento infinitesimal, as magnitudes da tensão normal e da tensão de cisalhamento são dadas por: ${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$

${\ displaystyle \ sigma _ {\ mathrm {n}} = {\ frac {1} {2}} (\ sigma _ {x} + \ sigma _ {y}) + {\ frac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ cos 2 \ theta + \ tau _ {xy} \ sin 2 \ theta}$

${\ displaystyle \ tau _ {\ mathrm {n}} = - {\ frac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ sin 2 \ theta + \ tau _ { xy} \ cos 2 \ theta}$

Derivação das equações paramétricas do círculo de Mohr - Equilíbrio de forças

A partir do equilíbrio de forças na direção do ( -eixo) (Figura 4), e sabendo que é a área do plano onde atua , temos: ${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle x '}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle dA}$ ${\ displaystyle \ {\ begin {alinhados} \ sum F_ {x '} & = \ sigma _ {\ mathrm {n}} dA- \ sigma _ {x} dA \ cos ^ {2} \ theta - \ sigma _ {y} dA \ sin ^ {2} \ theta - \ tau _ {xy} dA \ cos \ theta \ sin \ theta - \ tau _ {xy} dA \ sin \ theta \ cos \ theta = 0 \\\ sigma _ {\ mathrm {n}} & = \ sigma _ {x} \ cos ^ {2} \ theta + \ sigma _ {y} \ sin ^ {2} \ theta +2 \ tau _ {xy} \ sin \ theta \ cos \ theta \\\ end {alinhado}}}$ No entanto, sabendo que ${\ displaystyle \ cos ^ {2} \ theta = {\ frac {1+ \ cos 2 \ theta} {2}}, \ qquad \ sin ^ {2} \ theta = {\ frac {1- \ cos 2 \ theta} {2}} \ qquad {\ text {e}} \ qquad \ sin 2 \ theta = 2 \ sin \ theta \ cos \ theta}$ nós obtemos ${\ displaystyle \ sigma _ {\ mathrm {n}} = {\ frac {1} {2}} (\ sigma _ {x} + \ sigma _ {y}) + {\ frac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ cos 2 \ theta + \ tau _ {xy} \ sin 2 \ theta}$ Agora, a partir do equilíbrio de forças na direção do ( -eixo) (Figura 4), e sabendo que é a área do plano onde atua , temos: ${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle y '}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle dA}$ ${\ displaystyle \ {\ begin {alinhados} \ sum F_ {y '} & = \ tau _ {\ mathrm {n}} dA + \ sigma _ {x} dA \ cos \ theta \ sin \ theta - \ sigma _ { y} dA \ sin \ theta \ cos \ theta - \ tau _ {xy} dA \ cos ^ {2} \ theta + \ tau _ {xy} dA \ sin ^ {2} \ theta = 0 \\\ tau _ {\ mathrm {n}} & = - (\ sigma _ {x} - \ sigma _ {y}) \ sin \ theta \ cos \ theta + \ tau _ {xy} \ left (\ cos ^ {2} \ theta - \ sin ^ {2} \ theta \ right) \\\ end {alinhado}}}$ No entanto, sabendo que ${\ displaystyle \ cos ^ {2} \ theta - \ sin ^ {2} \ theta = \ cos 2 \ theta \ qquad {\ text {e}} \ qquad \ sin 2 \ theta = 2 \ sin \ theta \ cos \ theta}$ nós obtemos ${\ displaystyle \ tau _ {\ mathrm {n}} = - {\ frac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ sin 2 \ theta + \ tau _ { xy} \ cos 2 \ theta}$

Ambas as equações também podem ser obtidas aplicando-se a lei de transformação do tensor no conhecido tensor de tensão de Cauchy, que é equivalente a realizar o equilíbrio estático de forças na direção de e . ${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$

Derivação das equações paramétricas do círculo de Mohr - Transformação do tensor

A lei de transformação do tensor de tensão pode ser declarada como ${\ displaystyle {\ begin {align} {\ boldsymbol {\ sigma}} '& = \ mathbf {A} {\ boldsymbol {\ sigma}} \ mathbf {A} ^ {T} \\\ left [{\ begin {matriz} \ sigma _ {x '} & \ tau _ {x'y'} \\\ tau _ {y'x '} & \ sigma _ {y'} \\\ end {matriz}} \ direita] & = \ left [{\ begin {matrix} a_ {x} & a_ {xy} \\ a_ {yx} & a_ {y} \\\ end {matrix}} \ right] \ left [{\ begin {matrix} \ sigma _ {x} & \ tau _ {xy} \\\ tau _ {yx} & \ sigma _ {y} \\\ fim {matriz}} \ direita] \ esquerda [{\ begin {matriz} a_ {x } & a_ {yx} \\ a_ {xy} & a_ {y} \\\ end {matriz}} \ right] \\ & = \ left [{\ begin {matrix} \ cos \ theta & \ sin \ theta \\ - \ sin \ theta & \ cos \ theta \\\ end {matrix}} \ right] \ left [{\ begin {matrix} \ sigma _ {x} & \ tau _ {xy} \\\ tau _ {yx } & \ sigma _ {y} \\\ end {matriz}} \ right] \ left [{\ begin {matrix} \ cos \ theta & - \ sin \ theta \\\ sin \ theta & \ cos \ theta \ \\ end {matriz}} \ direita] \ end {alinhado}}}$ Expandindo o lado direito, e sabendo disso e , temos: ${\ displaystyle \ sigma _ {x '} = \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {x'y '} = \ tau _ {\ mathrm {n}}}$ ${\ displaystyle \ sigma _ {\ mathrm {n}} = \ sigma _ {x} \ cos ^ {2} \ theta + \ sigma _ {y} \ sin ^ {2} \ theta +2 \ tau _ {xy } \ sin \ theta \ cos \ theta}$ No entanto, sabendo que ${\ displaystyle \ cos ^ {2} \ theta = {\ frac {1+ \ cos 2 \ theta} {2}}, \ qquad \ sin ^ {2} \ theta = {\ frac {1- \ cos 2 \ theta} {2}} \ qquad {\ text {e}} \ qquad \ sin 2 \ theta = 2 \ sin \ theta \ cos \ theta}$ nós obtemos ${\ displaystyle \ sigma _ {\ mathrm {n}} = {\ frac {1} {2}} (\ sigma _ {x} + \ sigma _ {y}) + {\ frac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ cos 2 \ theta + \ tau _ {xy} \ sin 2 \ theta}$ ${\ displaystyle \ tau _ {\ mathrm {n}} = - (\ sigma _ {x} - \ sigma _ {y}) \ sin \ theta \ cos \ theta + \ tau _ {xy} \ left (\ cos ^ {2} \ theta - \ sin ^ {2} \ theta \ right)}$ No entanto, sabendo que ${\ displaystyle \ cos ^ {2} \ theta - \ sin ^ {2} \ theta = \ cos 2 \ theta \ qquad {\ text {e}} \ qquad \ sin 2 \ theta = 2 \ sin \ theta \ cos \ theta}$ nós obtemos ${\ displaystyle \ tau _ {\ mathrm {n}} = - {\ frac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ sin 2 \ theta + \ tau _ { xy} \ cos 2 \ theta}$ Não é necessário neste momento calcular o componente de tensão que atua no plano perpendicular ao plano de ação de, pois não é necessário para derivar a equação para o círculo de Mohr. ${\ displaystyle \ sigma _ {y '}}$${\ displaystyle \ sigma _ {x '}}$

Essas duas equações são as equações paramétricas do círculo de Mohr. Nessas equações, é o parâmetro e e são as coordenadas. Isso significa que ao escolher um sistema de coordenadas com abscissa e ordenada , dar valores ao parâmetro colocará os pontos obtidos em um círculo. ${\ displaystyle 2 \ theta}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle \ theta}$

Eliminar o parâmetro dessas equações paramétricas resultará na equação não paramétrica do círculo de Mohr. Isso pode ser alcançado reorganizando as equações para e , primeiro transpondo o primeiro termo na primeira equação e elevando ao quadrado ambos os lados de cada uma das equações e, em seguida, adicionando-os. Assim nós temos ${\ displaystyle 2 \ theta}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$

${\ displaystyle {\ begin {alinhados} \ left [\ sigma _ {\ mathrm {n}} - {\ tfrac {1} {2}} (\ sigma _ {x} + \ sigma _ {y}) \ right ] ^ {2} + \ tau _ {\ mathrm {n}} ^ {2} & = \ left [{\ tfrac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ right] ^ {2} + \ tau _ {xy} ^ {2} \\ (\ sigma _ {\ mathrm {n}} - \ sigma _ {\ mathrm {avg}}) ^ {2} + \ tau _ {\ mathrm {n}} ^ {2} & = R ^ {2} \ end {alinhado}}}$

Onde

${\ displaystyle R = {\ sqrt {\ left [{\ tfrac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ right] ^ {2} + \ tau _ {xy } ^ {2}}} \ quad {\ text {e}} \ quad \ sigma _ {\ mathrm {avg}} = {\ tfrac {1} {2}} (\ sigma _ {x} + \ sigma _ {y})}$

Esta é a equação de um círculo (o círculo de Mohr) da forma

${\ displaystyle (xa) ^ {2} + (yb) ^ {2} = r ^ {2}}$

com o raio centrado em um ponto com coordenadas no sistema de coordenadas. ${\ displaystyle r = R}$${\ displaystyle (a, b) = (\ sigma _ {\ mathrm {avg}}, 0)}$${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$

Convenções de assinatura

Existem dois conjuntos separados de convenções de sinais que precisam ser considerados ao usar o Círculo de Mohr: uma convenção de sinais para componentes de tensão no "espaço físico" e outra para componentes de tensão no "Espaço do Círculo de Mohr". Além disso, dentro de cada um dos dois conjuntos de convenções de sinais, os engenharia mecânica ( engenharia estrutural e de engenharia mecânica ) literatura segue uma convenção de sinal diferente do geomechanics literatura. Não há convenção de sinal padrão, e a escolha de uma convenção de sinal particular é influenciada pela conveniência para cálculo e interpretação para o problema particular em mãos. Uma explicação mais detalhada dessas convenções de sinais é apresentada abaixo.

A derivação anterior para a equação do Círculo de Mohr usando a Figura 4 segue a convenção de sinais da mecânica de engenharia. A convenção de sinais de mecânica de engenharia será usada para este artigo .

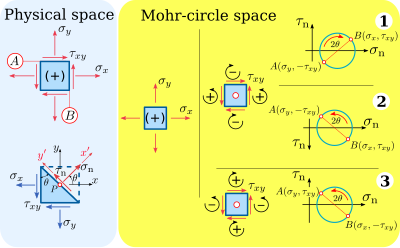
Convenção de sinalização de espaço físico

A partir da convenção do tensor de tensão de Cauchy (Figura 3 e Figura 4), o primeiro subscrito nos componentes de tensão denota a face na qual o componente de tensão atua, e o segundo subscrito indica a direção do componente de tensão. Assim, é a tensão de cisalhamento agindo na face com vetor normal na direção positiva do eixo e na direção positiva do eixo. ${\ displaystyle \ tau _ {xy}}$${\ displaystyle x}$${\ displaystyle y}$

Na convenção de signos do espaço físico, as tensões normais positivas estão para fora do plano de ação (tensão) e as tensões normais negativas estão para dentro do plano de ação (compressão) (Figura 5).

Na convenção de sinais do espaço físico, as tensões de cisalhamento positivas atuam nas faces positivas do elemento de material na direção positiva de um eixo. Além disso, as tensões de cisalhamento positivas atuam nas faces negativas do elemento de material na direção negativa de um eixo. Uma face positiva tem seu vetor normal na direção positiva de um eixo e uma face negativa tem seu vetor normal na direção negativa de um eixo. Por exemplo, as tensões de cisalhamento e são positivas porque atuam em faces positivas, e também atuam na direção positiva do eixo e do eixo, respectivamente (Figura 3). Da mesma forma, as respectivas tensões de cisalhamento opostas e atuando nas faces negativas têm um sinal negativo porque atuam na direção negativa do eixo e eixo, respectivamente. ${\ displaystyle \ tau _ {xy}}$${\ displaystyle \ tau _ {yx}}$${\ displaystyle y}$${\ displaystyle x}$${\ displaystyle \ tau _ {xy}}$${\ displaystyle \ tau _ {yx}}$${\ displaystyle x}$${\ displaystyle y}$

Convenção de sinalização de espaço circular de Mohr

Figura 5. Convenção de sinais de mecânica de engenharia para desenhar o círculo de Mohr. Este artigo segue a convenção de sinalização nº 3, conforme mostrado.

Na convenção de sinal de espaço circular de Mohr, tensões normais têm o mesmo sinal que tensões normais na convenção de sinal de espaço físico: tensões normais positivas atuam externamente ao plano de ação e tensões normais negativas atuam internamente ao plano de ação.

As tensões de cisalhamento, no entanto, têm uma convenção diferente no espaço do círculo de Mohr em comparação com a convenção no espaço físico. Na convenção de sinal de espaço circular de Mohr, as tensões de cisalhamento positivas giram o elemento de material no sentido anti-horário e as tensões de cisalhamento negativas giram o material no sentido horário. Dessa forma, o componente de tensão de cisalhamento é positivo no espaço do círculo de Mohr e o componente de tensão de cisalhamento é negativo no espaço do círculo de Mohr. ${\ displaystyle \ tau _ {xy}}$${\ displaystyle \ tau _ {yx}}$

Existem duas opções para desenhar o espaço do círculo de Mohr, que produzem um círculo de Mohr matematicamente correto:

1. Tensões de cisalhamento positivas são plotadas para cima (Figura 5, convenção de sinal nº 1)
2. As tensões de cisalhamento positivas são plotadas para baixo, ou seja, o eixo -é invertido (Figura 5, convenção de sinais nº 2).${\ displaystyle \ tau _ {\ mathrm {n}}}$

A plotagem das tensões de cisalhamento positivas para cima faz com que o ângulo no círculo de Mohr tenha uma rotação positiva no sentido horário, o que é oposto à convenção do espaço físico. É por isso que alguns autores preferem traçar as tensões de cisalhamento positivas para baixo, o que faz com que o ângulo no círculo de Mohr tenha uma rotação positiva no sentido anti-horário, semelhante à convenção do espaço físico para tensões de cisalhamento. ${\ displaystyle 2 \ theta}$${\ displaystyle 2 \ theta}$

Para superar o "problema" de ter o eixo da tensão de cisalhamento para baixo no espaço do círculo de Mohr, há uma convenção de sinalização alternativa em que as tensões de cisalhamento positivas giram o elemento de material no sentido horário e as tensões de cisalhamento negativas giram o elemento de material no sentido anti-horário (Figura 5, opção 3). Dessa forma, as tensões de cisalhamento positivas são plotadas para cima no espaço do círculo de Mohr e o ângulo tem uma rotação positiva no sentido anti-horário no espaço do círculo de Mohr. Esta convenção de sinal alternativa produz um círculo que é idêntico à convenção de sinal # 2 na Figura 5 porque uma tensão de cisalhamento positiva também é uma tensão de cisalhamento no sentido anti-horário, e ambas são plotadas para baixo. Além disso, uma tensão de cisalhamento negativa é uma tensão de cisalhamento no sentido horário e ambas são plotadas para cima. ${\ displaystyle 2 \ theta}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$

Este artigo segue a convenção de sinalização de mecânica de engenharia para o espaço físico e a convenção de sinalização alternativa para o espaço do círculo de Mohr (convenção de sinalização nº 3 na Figura 5)

Desenhando o círculo de Mohr

Figura 6. Círculo de Mohr para condições de tensão plana e deformação plana (abordagem de ângulo duplo) . Depois de uma análise de tensão, os componentes de tensão , e a um ponto de material são conhecidos. Esses componentes de tensão atuam em dois planos perpendiculares e de passagem . As coordenadas do ponto e do círculo de Mohr são os componentes de tensão atuando nos planos e no elemento material, respectivamente. O círculo de Mohr é então usado para encontrar os componentes de tensão e , isto é, as coordenadas de qualquer ponto de tensão no círculo, agindo em qualquer outro plano que esteja passando . O ângulo entre as linhas e é o dobro do ângulo entre os vetores normais dos planos e de passagem .${\ displaystyle \ sigma _ {x}}$${\ displaystyle \ sigma _ {y}}$${\ displaystyle \ tau _ {xy}}$${\ displaystyle P}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle P}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle D}$${\ displaystyle D}$${\ displaystyle P}$${\ displaystyle {\ overline {OB}}}$${\ displaystyle {\ overline {OD}}}$${\ displaystyle \ theta}$${\ displaystyle B}$${\ displaystyle D}$${\ displaystyle P}$

Assumindo que sabemos os componentes de tensão , e num ponto no objecto de estudo, tal como mostrado na Figura 4, são os seguintes os passos para a construção do círculo Mohr para o estado de stress em : ${\ displaystyle \ sigma _ {x}}$${\ displaystyle \ sigma _ {y}}$${\ displaystyle \ tau _ {xy}}$${\ displaystyle P}$${\ displaystyle P}$

1. Desenhe o sistema de coordenadas cartesianas com um eixo horizontal e um eixo vertical .${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$
2. Trace dois pontos e no espaço correspondente às conhecidas componentes de tensões em ambos os planos perpendiculares e , respectivamente (Figura 4 e 6), seguindo a convenção de sinal escolhida.${\ displaystyle A (\ sigma _ {y}, \ tau _ {xy})}$${\ displaystyle B (\ sigma _ {x}, - \ tau _ {xy})}$${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle A}$${\ displaystyle B}$
3. Desenhe o diâmetro do círculo unindo pontos e com uma linha reta .${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle {\ overline {AB}}}$
4. Desenhe o Círculo de Mohr . O centro do círculo é o ponto médio da linha do diâmetro , que corresponde à interseção dessa linha com o eixo.${\ displaystyle O}$${\ displaystyle {\ overline {AB}}}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$

Encontrando tensões normais principais

Componentes de tensão em um elemento rotativo 2D . Exemplo de como os componentes de tensão variam nas faces (arestas) de um elemento retangular conforme o ângulo de sua orientação varia. As tensões principais ocorrem quando as tensões de cisalhamento desaparecem simultaneamente de todas as faces. A orientação em que isso ocorre fornece as direções principais . Neste exemplo, quando o retângulo é horizontal, as tensões são dadas por${\ displaystyle \ left [{\ begin {matrix} \ sigma _ {xx} & \ tau _ {xy} \\\ tau _ {yx} & \ sigma _ {yy} \ end {matrix}} \ right] = \ left [{\ begin {matrix} -10 & 10 \\ 10 & 15 \ end {matrix}} \ right].}$

A magnitude das tensões principais são as abscissas dos pontos e (Figura 6) onde o círculo intercepta o eixo. A magnitude da maior tensão principal é sempre o maior valor absoluto da abcissa de qualquer um desses dois pontos. Da mesma forma, a magnitude da menor tensão principal é sempre o menor valor absoluto da abcissa desses dois pontos. Como esperado, as ordenadas desses dois pontos são zero, correspondendo à magnitude dos componentes da tensão de cisalhamento nos planos principais. Alternativamente, os valores das tensões principais podem ser encontrados por ${\ displaystyle C}$${\ displaystyle E}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ sigma _ {1}}$${\ displaystyle \ sigma _ {2}}$

${\ displaystyle \ sigma _ {1} = \ sigma _ {\ max} = \ sigma _ {\ text {avg}} + R}$

${\ displaystyle \ sigma _ {2} = \ sigma _ {\ min} = \ sigma _ {\ text {avg}} - R}$

onde a magnitude da tensão normal média é a abscissa do centro , dada por ${\ displaystyle \ sigma _ {\ text {avg}}}$${\ displaystyle O}$

${\ displaystyle \ sigma _ {\ text {avg}} = {\ tfrac {1} {2}} (\ sigma _ {x} + \ sigma _ {y})}$

e o comprimento do raio do círculo (com base na equação de um círculo passando por dois pontos), é dado por ${\ displaystyle R}$

${\ displaystyle R = {\ sqrt {\ left [{\ tfrac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ right] ^ {2} + \ tau _ {xy } ^ {2}}}}$

Encontrar tensões de cisalhamento máximas e mínimas

As tensões de cisalhamento máxima e mínima correspondem às ordenadas dos pontos mais alto e mais baixo do círculo, respectivamente. Esses pontos estão localizados na interseção do círculo com a linha vertical que passa pelo centro do círculo ,. Assim, a magnitude das tensões de cisalhamento máxima e mínima são iguais ao valor do raio do círculo${\ displaystyle O}$${\ displaystyle R}$

${\ displaystyle \ tau _ {\ max, \ min} = \ pm R}$

Encontrar componentes de tensão em um plano arbitrário

Como mencionado antes, após a análise de tensões bidimensional foi realizada sabemos que os componentes de tensão , e em um ponto material . Esses componentes de tensão atuam em dois planos perpendiculares e passando como mostrado nas Figuras 5 e 6. O círculo de Mohr é usado para encontrar os componentes de tensão e , ou seja, as coordenadas de qualquer ponto do círculo, agindo em qualquer outro plano que passa fazendo um ângulo com o avião . Para isso, duas abordagens podem ser utilizadas: o ângulo duplo e o Pólo ou origem dos planos. ${\ displaystyle \ sigma _ {x}}$${\ displaystyle \ sigma _ {y}}$${\ displaystyle \ tau _ {xy}}$${\ displaystyle P}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle P}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle D}$${\ displaystyle D}$${\ displaystyle P}$${\ displaystyle \ theta}$${\ displaystyle B}$

Ângulo duplo

Conforme mostrado na Figura 6, para determinar os componentes de tensão que atuam em um plano em um ângulo anti-horário em relação ao plano no qual atua, viajamos um ângulo na mesma direção anti-horário em torno do círculo do ponto de tensão conhecido a ponto , ou seja, um ângulo entre as linhas e no círculo de Mohr. ${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle D}$${\ displaystyle \ theta}$${\ displaystyle B}$${\ displaystyle \ sigma _ {x}}$${\ displaystyle 2 \ theta}$${\ displaystyle B (\ sigma _ {x}, - \ tau _ {xy})}$${\ displaystyle D (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle 2 \ theta}$${\ displaystyle {\ overline {OB}}}$${\ displaystyle {\ overline {OD}}}$

A abordagem de ângulo duplo se baseia no fato de que o ângulo entre os vetores normais para quaisquer dois planos físicos que passam (Figura 4) é a metade do ângulo entre duas linhas que unem seus pontos de tensão correspondentes no círculo de Mohr e o centro do círculo. ${\ displaystyle \ theta}$${\ displaystyle P}$${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$

Esta relação de ângulo duplo vem do fato de que as equações paramétricas para o círculo de Mohr são uma função de . Também pode ser visto que os planos e no elemento material ao redor da Figura 5 são separados por um ângulo , que no círculo de Mohr é representado por um ângulo (o dobro do ângulo). ${\ displaystyle 2 \ theta}$${\ displaystyle A}$${\ displaystyle B}$${\ displaystyle P}$${\ displaystyle \ theta = 90 ^ {\ circ}}$${\ displaystyle 180 ^ {\ circ}}$

Pólo ou origem dos aviões

Figura 7. Círculo de Mohr para condições de tensão plana e deformação plana (abordagem de pólo). Qualquer linha reta desenhada a partir do pólo cruzará o círculo de Mohr em um ponto que representa o estado de tensão em um plano inclinado na mesma orientação (paralelo) no espaço que essa linha.

A segunda abordagem envolve a determinação de um ponto no círculo de Mohr denominado pólo ou origem dos planos . Qualquer linha reta desenhada a partir do pólo cruzará o círculo de Mohr em um ponto que representa o estado de tensão em um plano inclinado na mesma orientação (paralelo) no espaço que essa linha. Portanto, conhecendo os componentes de tensão e em qualquer plano particular, pode-se desenhar uma linha paralela a esse plano através das coordenadas particulares e no círculo de Mohr e encontrar o pólo como a interseção dessa linha com o círculo de Mohr. Como exemplo, vamos assumir que tem um estado de tensão com componentes de tensão , e , como mostrado na Figura 7. Em primeiro lugar, pode-se desenhar uma linha a partir do ponto em paralelo ao plano de acção da , ou, se escolher outra forma, uma linha do ponto paralelo ao plano de ação de . A interseção de qualquer uma dessas duas linhas com o círculo de Mohr é o pólo. Uma vez que o pólo tenha sido determinado, para encontrar o estado de tensão em um plano fazendo um ângulo com a vertical, ou em outras palavras, um plano tendo seu vetor normal formando um ângulo com o plano horizontal, então podemos traçar uma linha a partir do pólo paralelo a esse plano (ver Figura 7). As tensões normal e de cisalhamento nesse plano são, então, as coordenadas do ponto de intersecção entre a linha e o círculo de Mohr. ${\ displaystyle \ sigma}$${\ displaystyle \ tau}$${\ displaystyle \ sigma _ {\ mathrm {n}}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$${\ displaystyle \ sigma _ {x}, \!}$${\ displaystyle \ sigma _ {y}, \!}$${\ displaystyle \ tau _ {xy}, \!}$${\ displaystyle B}$${\ displaystyle \ sigma _ {x}}$${\ displaystyle A}$${\ displaystyle \ sigma _ {y}}$${\ displaystyle \ theta}$${\ displaystyle \ theta}$

Encontrar a orientação dos planos principais

A orientação dos planos onde atuam as tensões principais máximas e mínimas, também conhecidos como planos principais , pode ser determinada medindo no círculo de Mohr os ângulos ∠BOC e ∠BOE, respectivamente, e tomando a metade de cada um desses ângulos. Assim, o ângulo ∠BOC entre e é o dobro do ângulo que o plano principal principal forma com o plano . ${\ displaystyle {\ overline {OB}}}$${\ displaystyle {\ overline {OC}}}$${\ displaystyle \ theta _ {p}}$${\ displaystyle B}$

Ângulos e também podem ser encontrados na seguinte equação ${\ displaystyle \ theta _ {p1}}$${\ displaystyle \ theta _ {p2}}$

${\ displaystyle \ tan 2 \ theta _ {\ mathrm {p}} = {\ frac {2 \ tau _ {xy}} {\ sigma _ {y} - \ sigma _ {x}}}}$

Esta equação define dois valores para que são separados (Figura). Esta equação pode ser derivada diretamente da geometria do círculo, ou fazendo a equação paramétrica do círculo igual a zero (a tensão de cisalhamento nos planos principais é sempre zero). ${\ displaystyle \ theta _ {\ mathrm {p}}}$${\ displaystyle 90 ^ {\ circ}}$${\ displaystyle \ tau _ {\ mathrm {n}}}$

Exemplo

Figura 8

Figura 9

Suponha um elemento de material sob um estado de tensão como mostrado na Figura 8 e Figura 9, com o plano de um de seus lados orientado 10 ° em relação ao plano horizontal. Usando o círculo de Mohr, encontre:

• A orientação de seus planos de ação.
• As tensões de cisalhamento máximas e a orientação de seus planos de ação.
• Os componentes de tensão em um plano horizontal.

Verifique as respostas usando as fórmulas de transformação de tensão ou a lei de transformação de tensão.

Solução: Seguindo a convenção de sinalização de mecânica de engenharia para o espaço físico (Figura 5), ​​os componentes de tensão para o elemento material neste exemplo são:

${\ displaystyle \ sigma _ {x '} = - 10 {\ textrm {MPa}}}$

${\ displaystyle \ sigma _ {y '} = 50 {\ textrm {MPa}}}$

${\ displaystyle \ tau _ {x'y '} = 40 {\ textrm {MPa}}}$.

Seguindo as etapas para desenhar o círculo de Mohr para este estado particular de tensão, primeiro desenhamos um sistema de coordenadas cartesianas com o eixo para cima. ${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle \ tau _ {\ mathrm {n}}}$

Em seguida, plotamos dois pontos A (50,40) e B (-10, -40), representando o estado de tensão no plano A e B, conforme mostrado na Figura 8 e na Figura 9. Esses pontos seguem a convenção de sinais de mecânica de engenharia para o espaço do círculo de Mohr (Figura 5), ​​que assume tensões normais positivas para fora do elemento de material e tensões de cisalhamento positivas em cada plano que gira o elemento de material no sentido horário. Dessa forma, a tensão de cisalhamento que atua no plano B é negativa e a tensão de cisalhamento que atua no plano A é positiva. O diâmetro do círculo é a linha que une os pontos A e B. O centro do círculo é a interseção desta linha com o eixo-. Sabendo a localização do centro e o comprimento do diâmetro, podemos traçar o círculo de Mohr para este estado particular de tensão. ${\ displaystyle \ sigma _ {\ mathrm {n}}}$

As abscissas de ambos os pontos E e C (Figura 8 e Figura 9) intersectando o eixo são as magnitudes das tensões normais mínima e máxima, respectivamente; as ordenadas de ambos os pontos E e C são as magnitudes das tensões de cisalhamento atuando nos planos principal e secundário, respectivamente, que é zero para os planos principais. ${\ displaystyle \ sigma _ {\ mathrm {n}}}$

Embora a ideia de usar o círculo de Mohr seja encontrar graficamente diferentes componentes de tensão medindo realmente as coordenadas para diferentes pontos no círculo, é mais conveniente confirmar os resultados analiticamente. Assim, o raio e a abscissa do centro do círculo são

${\ displaystyle {\ begin {alinhados} R & = {\ sqrt {\ left [{\ tfrac {1} {2}} (\ sigma _ {x} - \ sigma _ {y}) \ right] ^ {2} + \ tau _ {xy} ^ {2}}} \\ & = {\ sqrt {\ left [{\ tfrac {1} {2}} (- 10-50) \ right] ^ {2} + 40 ^ {2}}} \\ & = 50 {\ textrm {MPa}} \\\ end {alinhado}}}$

${\ displaystyle {\ begin {alinhados} \ sigma _ {\ mathrm {avg}} & = {\ tfrac {1} {2}} (\ sigma _ {x} + \ sigma _ {y}) \\ & = {\ tfrac {1} {2}} (- 10 + 50) \\ & = 20 {\ textrm {MPa}} \\\ end {alinhado}}}$

e as principais tensões são

${\ displaystyle {\ begin {alinhado} \ sigma _ {1} & = \ sigma _ {\ mathrm {avg}} + R \\ & = 70 {\ textrm {MPa}} \\\ end {alinhado}}}$

${\ displaystyle {\ begin {alinhado} \ sigma _ {2} & = \ sigma _ {\ mathrm {avg}} -R \\ & = - 30 {\ textrm {MPa}} \\\ end {alinhado}} }$

As coordenadas para os pontos H e G (Figura 8 e Figura 9) são as magnitudes das tensões de cisalhamento mínima e máxima, respectivamente; as abscissas para os pontos H e G são as magnitudes das tensões normais atuando nos mesmos planos onde atuam as tensões de cisalhamento mínima e máxima, respectivamente. As magnitudes das tensões de cisalhamento mínima e máxima podem ser encontradas analiticamente por

${\ displaystyle \ tau _ {\ max, \ min} = \ pm R = \ pm 50 {\ textrm {MPa}}}$

e as tensões normais atuando nos mesmos planos onde atuam as tensões de cisalhamento mínima e máxima são iguais a ${\ displaystyle \ sigma _ {\ mathrm {avg}}}$

Podemos escolher usar a abordagem de ângulo duplo (Figura 8) ou a abordagem de Pólo (Figura 9) para encontrar a orientação das tensões normais principais e tensões de cisalhamento principais.

Usando a abordagem de ângulo duplo, medimos os ângulos ∠BOC e ∠BOE no Círculo de Mohr (Figura 8) para encontrar o dobro do ângulo que a maior tensão principal e a menor tensão principal formam com o plano B no espaço físico. Para obter um valor mais preciso para esses ângulos, em vez de medir manualmente os ângulos, podemos usar a expressão analítica

${\ displaystyle {\ begin {alinhados} 2 \ theta _ {\ mathrm {p}} = \ arctan {\ frac {2 \ tau _ {xy}} {\ sigma _ {x} - \ sigma _ {y}} } = \ arctan {\ frac {2 * 40} {(- 10-50)}} = - \ arctan {\ frac {4} {3}} \ end {alinhado}}}$

Uma solução é: . Pela inspeção da Figura 8, este valor corresponde ao ângulo ∠BOE. Assim, o ângulo principal menor é ${\ displaystyle 2 \ theta _ {p} = - 53,13 ^ {\ circ}}$

${\ displaystyle \ theta _ {p2} = - 26,565 ^ {\ circ}}$

Então, o principal ângulo principal é

${\ displaystyle {\ begin {alinhado} 2 \ theta _ {p1} & = 180-53,13 ^ {\ circ} = 126,87 ^ {\ circ} \\\ theta _ {p1} & = 63,435 ^ {\ circ} \ \\ end {alinhado}}}$

Lembre-se de que, neste exemplo particular, e são ângulos em relação ao plano de ação de (orientados no eixo) e não ângulos em relação ao plano de ação de (orientados no eixo). ${\ displaystyle \ theta _ {p1}}$${\ displaystyle \ theta _ {p2}}$${\ displaystyle \ sigma _ {x '}}$${\ displaystyle x '}$${\ displaystyle \ sigma _ {x}}$${\ displaystyle x}$

Usando a abordagem de pólo, primeiro localizamos o pólo ou a origem dos planos. Para isso, traçamos através do ponto A do círculo de Mohr uma linha inclinada 10 ° com a horizontal, ou seja, uma linha paralela ao plano A onde atua. O pólo é onde esta linha cruza o círculo de Mohr (Figura 9). Para confirmar a localização do Pólo, poderíamos traçar uma linha através do ponto B no círculo de Mohr paralelo ao plano B onde atua. Esta linha também cruzaria o círculo de Mohr no Pólo (Figura 9). ${\ displaystyle \ sigma _ {y '}}$${\ displaystyle \ sigma _ {x '}}$

Do pólo, desenhamos linhas para diferentes pontos do círculo de Mohr. As coordenadas dos pontos onde essas linhas se cruzam com o círculo de Mohr indicam os componentes de tensão atuando em um plano no espaço físico com a mesma inclinação da linha. Por exemplo, a linha do Pólo ao ponto C no círculo tem a mesma inclinação do plano no espaço físico onde atua. Este plano faz um ângulo de 63,435 ° com o plano B, tanto no espaço do círculo de Mohr quanto no espaço físico. Da mesma forma, as linhas são traçadas do Pólo aos pontos E, D, F, G e H para encontrar os componentes de tensão em planos com a mesma orientação. ${\ displaystyle \ sigma _ {1}}$

Círculo de Mohr para um estado tridimensional geral de tensões

Figura 10. Círculo de Mohr para um estado tridimensional de tensão

Para construir o círculo de Mohr para um caso geral tridimensional de tensões em um ponto, os valores das tensões principais e suas direções principais devem ser avaliados primeiro. ${\ displaystyle \ left (\ sigma _ {1}, \ sigma _ {2}, \ sigma _ {3} \ right)}$ ${\ displaystyle \ left (n_ {1}, n_ {2}, n_ {3} \ right)}$

Considerando os eixos principais como o sistema de coordenadas, em vez da geral , , sistema de coordenadas, e partindo do princípio de que , em seguida, os componentes normais e de cisalhamento do vector de tensão , para um dado plano com unidade vector , satisfazer as seguintes equações ${\ displaystyle x_ {1}}$${\ displaystyle x_ {2}}$${\ displaystyle x_ {3}}$${\ displaystyle \ sigma _ {1}> \ sigma _ {2}> \ sigma _ {3}}$${\ displaystyle \ mathbf {T} ^ {(\ mathbf {n})}}$${\ displaystyle \ mathbf {n}}$

${\ displaystyle {\ begin {alinhado} \ left (T ^ {(n)} \ right) ^ {2} & = \ sigma _ {ij} \ sigma _ {ik} n_ {j} n_ {k} \\ \ sigma _ {\ mathrm {n}} ^ {2} + \ tau _ {\ mathrm {n}} ^ {2} & = \ sigma _ {1} ^ {2} n_ {1} ^ {2} + \ sigma _ {2} ^ {2} n_ {2} ^ {2} + \ sigma _ {3} ^ {2} n_ {3} ^ {2} \ end {alinhado}}}$

${\ displaystyle \ sigma _ {\ mathrm {n}} = \ sigma _ {1} n_ {1} ^ {2} + \ sigma _ {2} n_ {2} ^ {2} + \ sigma _ {3} n_ {3} ^ {2}.}$

Sabendo que , podemos resolver para , , , utilizando o método de eliminação de Gauss que produz ${\ displaystyle n_ {i} n_ {i} = n_ {1} ^ {2} + n_ {2} ^ {2} + n_ {3} ^ {2} = 1}$${\ displaystyle n_ {1} ^ {2}}$${\ displaystyle n_ {2} ^ {2}}$${\ displaystyle n_ {3} ^ {2}}$

${\ displaystyle {\ begin {alinhados} n_ {1} ^ {2} & = {\ frac {\ tau _ {\ mathrm {n}} ^ {2} + (\ sigma _ {\ mathrm {n}} - \ sigma _ {2}) (\ sigma _ {\ mathrm {n}} - \ sigma _ {3})} {(\ sigma _ {1} - \ sigma _ {2}) (\ sigma _ {1} - \ sigma _ {3})}} \ geq 0 \\ n_ {2} ^ {2} & = {\ frac {\ tau _ {\ mathrm {n}} ^ {2} + (\ sigma _ {\ mathrm {n}} - \ sigma _ {3}) (\ sigma _ {\ mathrm {n}} - \ sigma _ {1})} {(\ sigma _ {2} - \ sigma _ {3}) ( \ sigma _ {2} - \ sigma _ {1})}} \ geq 0 \\ n_ {3} ^ {2} & = {\ frac {\ tau _ {\ mathrm {n}} ^ {2} + (\ sigma _ {\ mathrm {n}} - \ sigma _ {1}) (\ sigma _ {\ mathrm {n}} - \ sigma _ {2})} {(\ sigma _ {3} - \ sigma _ {1}) (\ sigma _ {3} - \ sigma _ {2})}} \ geq 0. \ end {alinhado}}}$

Uma vez que , e não é negativo, os numeradores dessas equações satisfazem ${\ displaystyle \ sigma _ {1}> \ sigma _ {2}> \ sigma _ {3}}$${\ displaystyle (n_ {i}) ^ {2}}$

${\ displaystyle \ tau _ {\ mathrm {n}} ^ {2} + (\ sigma _ {\ mathrm {n}} - \ sigma _ {2}) (\ sigma _ {\ mathrm {n}} - \ sigma _ {3}) \ geq 0}$como o denominador e${\ displaystyle \ sigma _ {1} - \ sigma _ {2}> 0}$${\ displaystyle \ sigma _ {1} - \ sigma _ {3}> 0}$

${\ displaystyle \ tau _ {\ mathrm {n}} ^ {2} + (\ sigma _ {\ mathrm {n}} - \ sigma _ {3}) (\ sigma _ {\ mathrm {n}} - \ sigma _ {1}) \ leq 0}$como o denominador e${\ displaystyle \ sigma _ {2} - \ sigma _ {3}> 0}$${\ displaystyle \ sigma _ {2} - \ sigma _ {1} <0}$

${\ displaystyle \ tau _ {\ mathrm {n}} ^ {2} + (\ sigma _ {\ mathrm {n}} - \ sigma _ {1}) (\ sigma _ {\ mathrm {n}} - \ sigma _ {2}) \ geq 0}$como o denominador e${\ displaystyle \ sigma _ {3} - \ sigma _ {1} <0}$${\ displaystyle \ sigma _ {3} - \ sigma _ {2} <0.}$

Essas expressões podem ser reescritas como

${\ displaystyle {\ begin {alinhados} \ tau _ {\ mathrm {n}} ^ {2} + \ left [\ sigma _ {\ mathrm {n}} - {\ tfrac {1} {2}} (\ sigma _ {2} + \ sigma _ {3}) \ right] ^ {2} \ geq \ left ({\ tfrac {1} {2}} (\ sigma _ {2} - \ sigma _ {3}) \ right) ^ {2} \\\ tau _ {\ mathrm {n}} ^ {2} + \ left [\ sigma _ {\ mathrm {n}} - {\ tfrac {1} {2}} (\ sigma _ {1} + \ sigma _ {3}) \ right] ^ {2} \ leq \ left ({\ tfrac {1} {2}} (\ sigma _ {1} - \ sigma _ {3}) \ right) ^ {2} \\\ tau _ {\ mathrm {n}} ^ {2} + \ left [\ sigma _ {\ mathrm {n}} - {\ tfrac {1} {2}} (\ sigma _ {1} + \ sigma _ {2}) \ right] ^ {2} \ geq \ left ({\ tfrac {1} {2}} (\ sigma _ {1} - \ sigma _ {2}) \ direita) ^ {2} \\\ end {alinhado}}}$

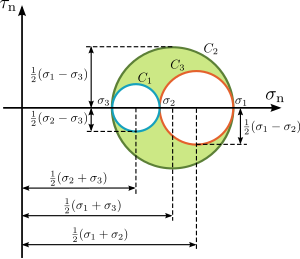
que são as equações dos três círculos de Mohr para o stress , e , com raios , e , e seus centros com coordenadas , , , respectivamente. ${\ displaystyle C_ {1}}$${\ displaystyle C_ {2}}$${\ displaystyle C_ {3}}$${\ displaystyle R_ {1} = {\ tfrac {1} {2}} (\ sigma _ {2} - \ sigma _ {3})}$${\ displaystyle R_ {2} = {\ tfrac {1} {2}} (\ sigma _ {1} - \ sigma _ {3})}$${\ displaystyle R_ {3} = {\ tfrac {1} {2}} (\ sigma _ {1} - \ sigma _ {2})}$${\ displaystyle \ left [{\ tfrac {1} {2}} (\ sigma _ {2} + \ sigma _ {3}), 0 \ right]}$${\ displaystyle \ left [{\ tfrac {1} {2}} (\ sigma _ {1} + \ sigma _ {3}), 0 \ right]}$${\ displaystyle \ left [{\ tfrac {1} {2}} (\ sigma _ {1} + \ sigma _ {2}), 0 \ right]}$

Essas equações para os círculos de Mohr mostram que todos os pontos de tensão admissíveis estão nesses círculos ou dentro da área sombreada entre eles (ver Figura 10). Os pontos de tensão que satisfazem a equação do círculo encontram-se dentro ou fora do círculo . Os pontos de tensão que satisfazem a equação do círculo ficam sobre ou dentro do círculo . E, finalmente, os pontos de estresse que satisfazem a equação para o círculo situam-se sobre, ou fora do círculo . ${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle C_ {1}}$${\ displaystyle C_ {1}}$${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle C_ {2}}$${\ displaystyle C_ {2}}$${\ displaystyle (\ sigma _ {\ mathrm {n}}, \ tau _ {\ mathrm {n}})}$${\ displaystyle C_ {3}}$${\ displaystyle C_ {3}}$

Veja também

• Análise do plano crítico

Referências

Bibliografia

• Cerveja, Ferdinand Pierre; Elwood Russell Johnston; John T. DeWolf (1992). Mecânica dos Materiais . McGraw-Hill Professional. ISBN 0-07-112939-1.
• Brady, BHG; ET Brown (1993). Rock Mechanics For Underground Mining (Terceira ed.). Kluwer Academic Publisher. pp. 17–29. ISBN 0-412-47550-2.
• Davis, RO; Selvadurai. APS (1996). Elasticidade e geomecânica . Cambridge University Press. pp. 16–26. ISBN 0-521-49827-9.
• Holtz, Robert D .; Kovacs, William D. (1981). Uma introdução à engenharia geotécnica . Série de engenharia civil e mecânica de engenharia Prentice-Hall. Prentice-Hall. ISBN 0-13-484394-0.
• Jaeger, John Conrad; Cook, NGW; Zimmerman, RW (2007). Fundamentos de mecânica das rochas (Quarta ed.). Wiley-Blackwell. pp. 9–41. ISBN 978-0-632-05759-7.
• Jumikis, Alfreds R. (1969). Mecânica teórica do solo: com aplicações práticas à mecânica do solo e engenharia de fundações . Van Nostrand Reinhold Co. ISBN 0-442-04199-3.
• Parry, Richard Hawley Gray (2004). Círculos de Mohr, caminhos de tensão e geotécnica (2 ed.). Taylor e Francis. pp. 1–30. ISBN 0-415-27297-1.
• Timoshenko, Stephen P .; James Norman Goodier (1970). Teoria da elasticidade (terceira ed.). Edições McGraw-Hill International. ISBN 0-07-085805-5.
• Timoshenko, Stephen P. (1983). História da resistência dos materiais: com um breve relato da história da teoria da elasticidade e teoria das estruturas . Dover Books on Physics. Publicações de Dover. ISBN 0-486-61187-6.

links externos

• Círculo de Mohr e mais círculos de Rebecca Brannon
• Pacote de Ensino e Aprendizagem DoITPoMS - "Análise de Estresse e Círculo de Mohr"