Teorema da Monodromia - Monodromy theorem

Ilustração da continuação analítica ao longo de uma curva (apenas um número finito de discos é mostrado). ${\ displaystyle U_ {t}}$

Continuação analítica ao longo de uma curva do logaritmo natural (a parte imaginária do logaritmo é mostrada apenas).

Na análise complexa , o teorema da monodromia é um resultado importante sobre a continuação analítica de uma função analítica complexa para um conjunto maior. A ideia é que se pode estender uma função analítica complexa (daqui em diante chamada simplesmente de função analítica ) ao longo de curvas começando no domínio original da função e terminando no conjunto maior. Um problema potencial dessa continuação analítica ao longo de uma estratégia de curva é que geralmente há muitas curvas que terminam no mesmo ponto no conjunto maior. O teorema da monodromia fornece condições suficientes para a continuação analítica para fornecer o mesmo valor em um determinado ponto, independentemente da curva usada para chegar lá, de modo que a função analítica estendida resultante seja bem definida e de valor único.

Antes de declarar este teorema, é necessário definir a continuação analítica ao longo de uma curva e estudar suas propriedades.

Continuação analítica ao longo de uma curva

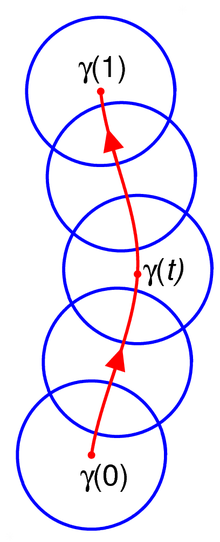
A definição de continuação analítica ao longo de uma curva é um pouco técnica, mas a ideia básica é que se começa com uma função analítica definida em torno de um ponto e se estende essa função ao longo de uma curva por meio de funções analíticas definidas em pequenos discos sobrepostos cobrindo essa curva.

Formalmente, considerar uma curva (uma função contínua ) Let ser uma função analítica definida em um disco aberto centrado em Uma continuação analítica do par ao longo é um conjunto de pares para tal que ${\ displaystyle \ gamma: [0,1] \ to \ mathbb {C}.}$${\ displaystyle f}$ ${\ displaystyle U}$${\ displaystyle \ gamma (0).}$${\ displaystyle (f, U)}$${\ displaystyle \ gamma}$${\ displaystyle (f_ {t}, U_ {t})}$${\ displaystyle 0 \ leq t \ leq 1}$

• ${\ displaystyle f_ {0} = f}$ e ${\ displaystyle U_ {0} = U.}$

• Para cada um é um disco aberto centrado em e é uma função analítica. ${\ displaystyle t \ in [0,1], U_ {t}}$${\ displaystyle \ gamma (t)}$${\ displaystyle f_ {t}: U_ {t} \ to \ mathbb {C}}$

• Para cada um existe tal que para todos com um tem isso (o que implica isso e tem uma interseção não vazia ) e as funções e coincidem na interseção ${\ displaystyle t \ in [0,1]}$${\ displaystyle \ varepsilon> 0}$${\ displaystyle t '\ in [0,1]}$${\ displaystyle | t-t '| <\ varepsilon}$${\ displaystyle \ gamma (t ') \ in U_ {t}}$${\ displaystyle U_ {t}}$${\ displaystyle U_ {t '}}$${\ displaystyle f_ {t}}$${\ displaystyle f_ {t '}}$${\ displaystyle U_ {t} \ cap U_ {t '}.}$

Propriedades de continuação analítica ao longo de uma curva

A continuação analítica ao longo de uma curva é essencialmente única, no sentido de que dadas duas continuações analíticas e de ao longo das funções e coincidem Informalmente, isso diz que quaisquer duas continuações analíticas de ao longo acabarão com os mesmos valores em uma vizinhança de ${\ displaystyle (f_ {t}, U_ {t})}$${\ displaystyle (g_ {t}, V_ {t})}$ ${\ displaystyle (0 \ leq t \ leq 1)}$${\ displaystyle (f, U)}$${\ displaystyle \ gamma,}$${\ displaystyle f_ {1}}$${\ displaystyle g_ {1}}$${\ displaystyle U_ {1} \ cap V_ {1}.}$${\ displaystyle (f, U)}$${\ displaystyle \ gamma}$${\ displaystyle \ gamma (1).}$

Se a curva é fechada (ou seja, ), não é necessário ter igual em uma vizinhança de. Por exemplo, se alguém começa em um ponto com e o logaritmo complexo definido em uma vizinhança deste ponto, e se deixa ser o círculo de raio centralizado na origem (viajado no sentido anti-horário de ), então, fazendo uma continuação analítica ao longo desta curva, terminará com um valor do logaritmo no qual é mais o valor original (veja a segunda ilustração à direita). ${\ displaystyle \ gamma}$${\ displaystyle \ gamma (0) = \ gamma (1)}$${\ displaystyle f_ {0}}$${\ displaystyle f_ {1}}$${\ displaystyle \ gamma (0).}$${\ displaystyle (a, 0)}$${\ displaystyle a> 0}$${\ displaystyle \ gamma}$${\ displaystyle a}$${\ displaystyle (a, 0)}$${\ displaystyle (a, 0)}$${\ displaystyle 2 \ pi i}$

Teorema da Monodromia

A homotopia com endopontos fixos é necessária para que o teorema da monodromia seja válido.

Conforme observado anteriormente, duas continuações analíticas ao longo da mesma curva produzem o mesmo resultado no ponto final da curva. No entanto, dadas duas curvas diferentes se ramificando a partir do mesmo ponto em torno do qual uma função analítica é definida, com as curvas se reconectando no final, não é verdade em geral que as continuações analíticas dessa função ao longo das duas curvas produzirão o mesmo valor em seu ponto final comum.

De fato, pode-se considerar, como na seção anterior, o logaritmo complexo definido em uma vizinhança de um ponto e o círculo centrado na origem e no raio. Então, é possível viajar de para de duas maneiras, no sentido anti-horário, na metade superior arco plano deste círculo, e no sentido horário, no arco do meio plano inferior. Os valores do logaritmo obtido pela continuação analítica ao longo desses dois arcos serão diferentes por ${\ displaystyle (a, 0)}$${\ displaystyle a.}$${\ displaystyle (a, 0)}$${\ displaystyle (-a, 0)}$${\ displaystyle (-a, 0)}$${\ displaystyle 2 \ pi i.}$

Se, no entanto, alguém pode deformar continuamente uma das curvas em outra, mantendo os pontos iniciais e finais fixos, e a continuação analítica é possível em cada uma das curvas intermediárias, então as continuações analíticas ao longo das duas curvas produzirão os mesmos resultados em seu ponto final comum. Isso é chamado de teorema da monodromia e sua afirmação é feita com precisão a seguir.

Seja um disco aberto no plano complexo centrado em um ponto e seja uma função analítica complexa. Deixe ser outro ponto no plano complexo. Se existe uma família de curvas com tal que e para todas a função é contínua, e para cada uma é possível fazer uma continuação analítica de along, então as continuações analíticas de along e produzirão os mesmos valores em ${\ displaystyle U}$${\ displaystyle P}$${\ displaystyle f: U \ to \ mathbb {C}}$${\ displaystyle Q}$${\ displaystyle \ gamma _ {s}: [0,1] \ to \ mathbb {C}}$${\ displaystyle s \ in [0,1]}$${\ displaystyle \ gamma _ {s} (0) = P}$${\ displaystyle \ gamma _ {s} (1) = Q}$${\ displaystyle s \ in [0,1],}$${\ displaystyle (s, t) \ in [0,1] \ times [0,1] \ to \ gamma _ {s} (t) \ in \ mathbb {C}}$${\ displaystyle s \ in [0,1]}$${\ displaystyle f}$${\ displaystyle \ gamma _ {s},}$${\ displaystyle f}$${\ displaystyle \ gamma _ {0}}$${\ displaystyle \ gamma _ {1}}$${\ displaystyle Q.}$

O teorema da monodromia torna possível estender uma função analítica a um conjunto maior por meio de curvas conectando um ponto no domínio original da função a pontos no conjunto maior. O teorema abaixo do qual afirma isso também é chamado de teorema da monodromia.

Seja um disco aberto no plano complexo centrado em um ponto e seja uma função analítica complexa. Se é um conjunto aberto simplesmente conectado contendo e é possível realizar uma continuação analítica de em qualquer curva contida na qual começa em, então admite uma continuação analítica direta para significar que existe uma função analítica complexa cuja restrição é ${\ displaystyle U}$${\ displaystyle P}$${\ displaystyle f: U \ to \ mathbb {C}}$${\ displaystyle W}$${\ displaystyle U,}$${\ displaystyle f}$${\ displaystyle W}$${\ displaystyle P,}$${\ displaystyle f}$${\ displaystyle W,}$${\ displaystyle g: W \ to \ mathbb {C}}$${\ displaystyle U}$${\ displaystyle f.}$

Veja também

• Continuação analítica
• Monodromia

Referências

• Krantz, Steven G. (1999). Manual de variáveis ​​complexas . Birkhäuser. ISBN   0-8176-4011-8 .
• Jones, Gareth A .; Singerman, David (1987). Funções complexas: um ponto de vista algébrico e geométrico . Cambridge University Press. ISBN   0-521-31366-X .

• Triebel, Hans (1986). Análise e física matemática, ed . Inglês . D. Reidel Pub. Co. ISBN   90-277-2077-0 .

links externos

• Teorema da monodromia em MathWorld
• Teorema da monodromia em PlanetMath .
• Teorema da monodromia na Enciclopédia da Matemática