Regressão não linear - Nonlinear regression

Parte de uma série sobre
Análise de regressão
Modelos
Regressão linear Regressão simples Regressão polinomial Modelo linear geral
Modelo linear generalizado Escolha discreta Regressão binomial Regressão binária Regressão logística Regressão logística multinomial Logit misto Probit Probit multinomial Logit ordenado Probit ordenado Poisson
Modelo multinível Efeitos fixos Efeitos aleatórios Modelo linear de efeitos mistos Modelo de efeitos mistos não linear
Regressão não linear Não paramétrico Semiparamétrico Robusto Quantil Isotônico Componentes principais Ângulo mínimo Local Segmentado
Erros em variáveis
Estimativa
Mínimos quadrados Linear Não linear
Ordinário Pesada Generalizado
Parcial Total Não negativo Regressão de cume Regularizado
Desvios mínimos absolutos Reponderado iterativamente Bayesiano Multivariada bayesiana
Fundo
Validação de regressão Resposta média e prevista Erros e residuais Qualidade de ajuste Resíduo estudantizado Teorema de Gauss-Markov
Portal de matemática
v t e

Em estatística, a regressão não linear é uma forma de análise de regressão na qual os dados observacionais são modelados por uma função que é uma combinação não linear dos parâmetros do modelo e depende de uma ou mais variáveis ​​independentes. Os dados são ajustados por um método de aproximações sucessivas.

Em geral

Na regressão não linear, um modelo estatístico do formulário,

${\ displaystyle \ mathbf {y} \ sim f (\ mathbf {x}, {\ boldsymbol {\ beta}})}$

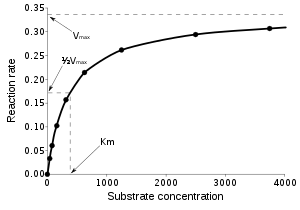
refere-se um vector de variáveis independentes , e seus observados associados variáveis dependentes , . A função é não linear nas componentes do vetor de parâmetros , mas de outra forma arbitrária. Por exemplo, o modelo Michaelis-Menten para a cinética enzimática tem dois parâmetros e uma variável independente, relacionados por: ${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {y}}$${\ displaystyle f}$${\ displaystyle \ beta}$${\ displaystyle f}$

${\ displaystyle f (x, {\ boldsymbol {\ beta}}) = {\ frac {\ beta _ {1} x} {\ beta _ {2} + x}}}$

Esta função é não linear porque não pode ser expressa como uma combinação linear dos dois s. ${\ displaystyle \ beta}$

Erro sistemático pode estar presente nas variáveis ​​independentes, mas seu tratamento está fora do escopo da análise de regressão. Se as variáveis ​​independentes não estiverem isentas de erros, trata-se de um modelo de erros nas variáveis , também fora deste escopo.

Outros exemplos de funções não lineares incluem funções exponenciais , funções logarítmicas , funções trigonométricas , funções de potência , função Gaussiana e distribuições de Lorentz . Algumas funções, como as funções exponenciais ou logarítmicas, podem ser transformadas para que sejam lineares. Quando assim transformado, a regressão linear padrão pode ser realizada, mas deve ser aplicada com cautela. Consulte Linearização§Transformação , abaixo, para obter mais detalhes.

Em geral, não há expressão de forma fechada para os parâmetros de melhor ajuste, como ocorre na regressão linear . Normalmente, algoritmos de otimização numérica são aplicados para determinar os parâmetros de melhor ajuste. Novamente em contraste com a regressão linear, pode haver muitos mínimos locais da função a ser otimizada e até mesmo o mínimo global pode produzir uma estimativa enviesada . Na prática, os valores estimados dos parâmetros são usados, em conjunto com o algoritmo de otimização, para tentar encontrar o mínimo global de uma soma de quadrados.

Para obter detalhes sobre modelagem de dados não lineares, consulte mínimos quadrados e mínimos quadrados não lineares .

Estatísticas de regressão

A suposição subjacente a este procedimento é que o modelo pode ser aproximado por uma função linear, ou seja, uma série de Taylor de primeira ordem :

${\ displaystyle f (x_ {i}, {\ boldsymbol {\ beta}}) \ approx f (x_ {i}, 0) + \ sum _ {j} J_ {ij} \ beta _ {j}}$

onde . Conclui-se que os estimadores de mínimos quadrados são dados por ${\ displaystyle J_ {ij} = {\ frac {\ partial f (x_ {i}, {\ boldsymbol {\ beta}})} {\ partial \ beta _ {j}}}}$

${\ displaystyle {\ hat {\ boldsymbol {\ beta}}} \ approx \ mathbf {(J ^ {T} J) ^ {- 1} J ^ {T} y}.}$

As estatísticas de regressão não linear são calculadas e usadas como nas estatísticas de regressão linear, mas usando J no lugar de X nas fórmulas. A aproximação linear introduz viés nas estatísticas. Portanto, é necessário mais cuidado do que o normal na interpretação de estatísticas derivadas de um modelo não linear.

Mínimos quadrados ordinários e ponderados

A curva de melhor ajuste é freqüentemente assumida como aquela que minimiza a soma dos resíduos quadrados . Esta é a abordagem de mínimos quadrados ordinários (OLS). No entanto, nos casos em que a variável dependente não tem variância constante, uma soma dos resíduos quadrados ponderados pode ser minimizada; veja os mínimos quadrados ponderados . Cada peso deve ser idealmente igual ao recíproco da variância da observação, mas os pesos podem ser recalculados em cada iteração, em um algoritmo de mínimos quadrados com ponderação iterativa.

Linearização

Transformação

Alguns problemas de regressão não linear podem ser movidos para um domínio linear por uma transformação adequada da formulação do modelo.

Por exemplo, considere o problema de regressão não linear

${\ displaystyle y = ae ^ {bx} U \, \!}$

com os parâmetros a e b e com multiplicativo termo de erro U . Se tomarmos o logaritmo de ambos os lados, isso se torna

${\ displaystyle \ ln {(y)} = \ ln {(a)} + bx + u, \, \!}$

onde u = ln ( U ), sugerindo estimativa dos parâmetros desconhecidos por uma regressão linear de ln ( y ) em x , um cálculo que não requer otimização iterativa. No entanto, o uso de uma transformação não linear requer cautela. As influências dos valores dos dados mudarão, assim como a estrutura de erro do modelo e a interpretação de quaisquer resultados inferenciais. Esses podem não ser os efeitos desejados. Por outro lado, dependendo de qual é a maior fonte de erro, uma transformação não linear pode distribuir os erros de forma gaussiana, então a escolha de realizar uma transformação não linear deve ser informada por considerações de modelagem.

Para a cinética de Michaelis-Menten , o gráfico linear Lineweaver-Burk

${\ displaystyle {\ frac {1} {v}} = {\ frac {1} {V _ {\ max}}} + {\ frac {K_ {m}} {V _ {\ max} [S]}}}$

de 1 / v contra 1 / [ S ] tem sido muito usado. No entanto, uma vez que é muito sensível a erros de dados e fortemente inclinado a ajustar os dados em um intervalo particular da variável independente, [ S ], seu uso é fortemente desencorajado.

Para distribuições de erro que pertencem à família exponencial , uma função de ligação pode ser usada para transformar os parâmetros sob a estrutura do modelo linear generalizado .

Segmentação

A variável independente ou explicativa (digamos X) pode ser dividida em classes ou segmentos e a regressão linear pode ser realizada por segmento. A regressão segmentada com análise de confiança pode produzir o resultado de que a variável dependente ou de resposta (digamos Y) se comporta de maneira diferente nos vários segmentos.

A figura mostra que a salinidade do solo (X) inicialmente não exerce influência no rendimento da cultura (Y) da mostarda, até um valor crítico ou limiar ( breakpoint ), após o qual o rendimento é afetado negativamente.

Veja também

• Mínimos quadrados não lineares
• Ajuste de curva
• Modelo linear generalizado
• Regressão local
• Metodologia de modelagem de resposta

Referências

Notas

Leitura adicional

• Bethea, RM; Duran, BS; Boullion, TL (1985). Métodos estatísticos para engenheiros e cientistas . Nova York: Marcel Dekker. ISBN 0-8247-7227-X.
• Meade, N .; Islam, T. (1995). "Intervalos de previsão para previsões da curva de crescimento". Journal of Forecasting . 14 (5): 413–430. doi : 10.1002 / for.3980140502 .
• Schittkowski, K. (2002). Ajuste de dados em sistemas dinâmicos . Boston: Kluwer. ISBN 1402010796.
• Seber, GAF; Wild, CJ (1989). Regressão não linear . Nova York: John Wiley and Sons. ISBN 0471617601.