Sistema sobredeterminado - Overdetermined system

Em matemática , um sistema de equações é considerado sobredeterminado se houver mais equações do que incógnitas. Um sistema sobredeterminado é quase sempre inconsistente (não tem solução) quando construído com coeficientes aleatórios. Porém, um sistema sobredeterminado terá soluções em alguns casos, por exemplo, se alguma equação ocorrer várias vezes no sistema, ou se algumas equações forem combinações lineares de outras.

A terminologia pode ser descrita em termos do conceito de contagem de restrições . Cada desconhecido pode ser visto como um grau de liberdade disponível. Cada equação introduzida no sistema pode ser vista como uma restrição que restringe um grau de liberdade . Portanto, o caso crítico ocorre quando o número de equações e o número de variáveis livres são iguais. Para cada variável que dá um grau de liberdade, existe uma restrição correspondente. O caso sobredeterminado ocorre quando o sistema foi excessivamente restrito - isto é, quando as equações superam as incógnitas. Em contraste, o subdeterminadoO caso ocorre quando o sistema foi sub-restringido - isto é, quando o número de equações é menor que o número de incógnitas. Esses sistemas geralmente têm um número infinito de soluções.

Sistemas de equações

Um exemplo em duas dimensões

# 1 Um sistema de três equações linearmente independentes, três linhas, sem soluções

# 2 Um sistema de três equações linearmente independentes, três linhas (duas paralelas ), sem soluções

# 3 Um sistema de três equações linearmente independentes, três linhas (todas paralelas), sem soluções

# 4 Um sistema de três equações (uma equação linearmente dependente das outras), três linhas (duas coincidentes), uma solução

# 5 Um sistema de três equações (uma equação linearmente dependente das outras), três linhas, uma solução

# 6 Um sistema de três equações (duas equações, cada uma linearmente dependente da terceira), três linhas coincidentes, uma infinidade de soluções

Considere o sistema de 3 equações e 2 incógnitas ( $X$ e $Y$ ), que é sobredeterminado porque 3> 2, e que corresponde ao Diagrama # 1:

{\ displaystyle {\ begin {alinhado} Y & = - 2X-1 \\ Y & = 3X-2 \\ Y & = X + 1. \ end {alinhado}}}

Há uma solução para cada par de equações lineares: para a primeira e segunda equações (0,2, −1,4), para a primeira e a terceira (−2/3, 1/3) e para a segunda e a terceira (1,5, 2,5 ) No entanto, não há solução que satisfaça todos os três simultaneamente. Os diagramas 2 e 3 mostram outras configurações que são inconsistentes porque nenhum ponto está em todas as linhas. Os sistemas desta variedade são considerados inconsistentes .

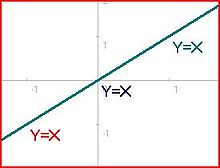
Os únicos casos em que o sistema sobredeterminado de fato tem uma solução são demonstrados nos Diagramas 4, 5 e 6. Essas exceções podem ocorrer apenas quando o sistema sobredeterminado contém equações linearmente dependentes o suficiente para que o número de equações independentes não exceda o número de desconhecidos. Dependência linear significa que algumas equações podem ser obtidas combinando linearmente outras equações. Por exemplo, Y = X + 1 e 2 Y = 2 X + 2 são equações linearmente dependentes porque a segunda pode ser obtida tomando duas vezes a primeira.

Forma de matriz

Qualquer sistema de equações lineares pode ser escrito como uma equação matricial . O sistema de equações anterior (no Diagrama 1) pode ser escrito da seguinte forma:

{\ displaystyle {\ begin {bmatrix} 2 & 1 \\ - 3 & 1 \\ - 1 & 1 \\\ end {bmatrix}} {\ begin {bmatrix} X \\ Y \\\ end {bmatrix}} = {\ begin {bmatrix } -1 \\ - 2 \\ 1 \\\ end {bmatrix}}}

Observe que as linhas da matriz de coeficiente (correspondendo a equações) superam as colunas (correspondendo a incógnitas), o que significa que o sistema está sobredeterminado. A classificação dessa matriz é 2, que corresponde ao número de variáveis dependentes no sistema. Um sistema linear é consistente se e somente se a matriz de coeficiente tiver a mesma classificação de sua matriz aumentada (a matriz de coeficiente com uma coluna extra adicionada, sendo essa coluna o vetor coluna de constantes). A matriz aumentada possui classificação 3, portanto, o sistema é inconsistente. A nulidade é 0, o que significa que o espaço nulo contém apenas o vetor zero e, portanto, não tem base .

Na álgebra linear, os conceitos de espaço de linha , espaço de coluna e espaço nulo são importantes para determinar as propriedades das matrizes. A discussão informal de restrições e graus de liberdade acima se relaciona diretamente a esses conceitos mais formais.

Caso homogêneo

O caso homogêneo (em que todos os termos constantes são zero) é sempre consistente (porque existe uma solução trivial, totalmente zero). Existem dois casos, dependendo do número de equações linearmente dependentes: ou existe apenas a solução trivial , ou existe a solução trivial mais um conjunto infinito de outras soluções.

Considere o sistema de equações lineares: L _i = 0 para 1 ≤ i ≤ M , e as variáveis X ₁ , X ₂ , ..., X _N , onde cada L _i é uma soma ponderada de X _i s. Então, X ₁ = X ₂ = ⋯ = X _N = 0 é sempre uma solução. Quando M < N, o sistema está subdeterminado e sempre há uma infinidade de outras soluções. De facto, a dimensão do espaço de soluções é sempre, pelo menos, N - M .

Para M ≥ N , pode não haver outra solução senão todos os valores sendo 0. Haverá uma infinidade de outras soluções apenas quando o sistema de equações tiver dependências suficientes (equações linearmente dependentes) para que o número de equações independentes seja no máximo N - 1. Mas com M ≥ N o número de equações independentes pode ser tão alto quanto N , caso em que a solução trivial é a única.

Caso não homogêneo

Em sistemas de equações lineares, L _i = c _i para 1 ≤ i ≤ M , nas variáveis X ₁ , X ₂ , ..., X _N as equações às vezes são linearmente dependentes; na verdade, o número de equações linearmente independentes não pode exceder N +1. Temos os seguintes casos possíveis para um sistema sobredeterminado com N incógnitas e M equações ( M > N ).

M = N +1 e todas as equações M são linearmente independentes . Este caso não produz solução. Exemplo: x = 1, x = 2.
M > N, mas apenas K equações ( K < M e K ≤ N +1) são linearmente independentes. Existem três subcasos possíveis disso:
- K = N +1. Este caso não produz soluções. Exemplo: 2 x = 2, x = 1, x = 2.
- K = N . Este caso produz uma única solução ou nenhuma solução, a última ocorrendo quando o vetor de coeficiente de uma equação pode ser replicado por uma soma ponderada dos vetores de coeficiente das outras equações, mas essa soma ponderada aplicada aos termos constantes das outras equações não não replicar o termo constante de uma equação. Exemplo com uma solução: 2 x = 2, x = 1. Exemplo sem solução: 2 x + 2 y = 2, x + y = 1, x + y = 3.
- K < N . Este caso produz infinitamente muitas soluções ou nenhuma solução, a última ocorrendo como no sub-caso anterior. Exemplo com infinitas soluções: 3 x + 3 y = 3, 2 x + 2 y = 2, x + y = 1. Exemplo sem solução: 3 x + 3 y + 3 z = 3, 2 x + 2 y + 2 z = 2, x + y + z = 1, x + y + z = 4.

Esses resultados podem ser mais fáceis de entender colocando a matriz aumentada dos coeficientes do sistema na forma escalonada de linha usando a eliminação de Gauss . Esta forma escalonada de linha é a matriz aumentada de um sistema de equações que é equivalente ao sistema dado (tem exatamente as mesmas soluções). O número de equações independentes no sistema original é o número de linhas diferentes de zero na forma escalonada. O sistema é inconsistente (sem solução) se e somente se a última linha diferente de zero na forma escalonada tiver apenas uma entrada diferente de zero que está na última coluna (dando uma equação 0 = c onde c é uma constante diferente de zero) . Caso contrário, há exatamente uma solução quando o número de linhas diferentes de zero na forma escalonada é igual ao número de incógnitas, e há infinitas soluções quando o número de linhas diferentes de zero é menor que o número de variáveis.

Colocando de outra forma, de acordo com o teorema de Rouché-Capelli , qualquer sistema de equações (sobredeterminado ou não) é inconsistente se a classificação da matriz aumentada for maior que a classificação da matriz de coeficientes . Se, por outro lado, os ranks dessas duas matrizes são iguais, o sistema deve ter pelo menos uma solução. A solução é única se e somente se a classificação for igual ao número de variáveis. Caso contrário, a solução geral tem k parâmetros livres onde k é a diferença entre o número de variáveis e o posto; portanto, em tal caso, há uma infinidade de soluções.

Soluções exatas

Todas as soluções exatas podem ser obtidas, ou pode ser mostrado que nenhuma existe, usando álgebra matricial . Veja Sistema de equações lineares # Solução de matriz .

Soluções aproximadas

O método dos mínimos quadrados ordinários pode ser usado para encontrar uma solução aproximada para sistemas sobredeterminados. Para o sistema, a fórmula dos mínimos quadrados é obtida a partir do problema ${\ displaystyle A \ mathbf {x} = \ mathbf {b},}$

{\ displaystyle \ min _ {\ mathbf {x}} \ lVert A \ mathbf {x} - \ mathbf {b} \ rVert,}

cuja solução pode ser escrita com as equações normais ,

{\ displaystyle \ mathbf {x} = \ left (A ^ {\ mathsf {T}} A \ right) ^ {- 1} A ^ {\ mathsf {T}} \ mathbf {b},}

onde indica uma transposição de matriz , desde que exista (ou seja, desde que A tenha classificação de coluna completa ). Com esta fórmula, uma solução aproximada é encontrada quando não existe uma solução exata, e dá uma solução exata quando uma existe. No entanto, para obter uma boa precisão numérica, é preferível usar a fatoração QR de A para resolver o problema dos mínimos quadrados. ${\ displaystyle {\ mathsf {T}}}$ ${\ displaystyle \ left (A ^ {\ mathsf {T}} A \ right) ^ {- 1}}$

Em uso geral

O conceito também pode ser aplicado a sistemas de equações mais gerais, como sistemas de equações polinomiais ou equações diferenciais parciais . No caso dos sistemas de equações polinomiais, pode acontecer que um sistema sobredeterminado tenha solução, mas nenhuma equação seja consequência das outras e que, ao retirar alguma equação, o novo sistema tenha mais soluções. Por exemplo, tem a solução única, mas cada equação por si só tem duas soluções. ${\ displaystyle (x-1) (x-2) = 0, (x-1) (x-3) = 0}$ ${\ displaystyle x = 1,}$

Veja também

Referências

^ "Planet Math, Overdetermined" .
^ Suave (06-12-2012). Álgebra Linear Numérica para Aplicações em Estatística . ISBN 9781461206231.
^ Stevens, Scott A. "System Analysis - Rank and Nullity" (PDF) . Matemática 220 - Apostilas de matrizes . Universidade Estadual da Pensilvânia . Retirado em 3 de abril de 2017 .
^ Anton, Howard; Rorres, Chris (2005). Elementary Linear Algebra (9ª ed.). John Wiley and Sons, Inc. ISBN 978-0-471-66959-3.
^ Trefethen, Lloyd; Bau, III, David (1997). Álgebra Linear Numérica . ISBN 978-0898713619.

[1] "Planet Math, Overdetermined" .

[2] Suave (06-12-2012). Álgebra Linear Numérica para Aplicações em Estatística . ISBN 9781461206231.

[3] Stevens, Scott A. "System Analysis - Rank and Nullity" (PDF) . Matemática 220 - Apostilas de matrizes . Universidade Estadual da Pensilvânia . Retirado em 3 de abril de 2017 .

[4] Anton, Howard; Rorres, Chris (2005). Elementary Linear Algebra (9ª ed.). John Wiley and Sons, Inc. ISBN 978-0-471-66959-3.

[5] Trefethen, Lloyd; Bau, III, David (1997). Álgebra Linear Numérica . ISBN 978-0898713619.

Languages

In other projects