Conjunto parcialmente ordenado - Partially ordered set

Em matemática , especialmente na teoria da ordem , um conjunto parcialmente ordenado (também poset ) formaliza e generaliza o conceito intuitivo de uma ordenação, sequenciamento ou arranjo dos elementos de um conjunto . Um poset consiste em um conjunto junto com uma relação binária indicando que, para certos pares de elementos no conjunto, um dos elementos precede o outro na ordenação. A própria relação é chamada de "ordem parcial". A palavra parcial nos nomes "ordem parcial" e "conjunto parcialmente ordenado" é usada como uma indicação de que nem todos os pares de elementos precisam ser comparáveis. Ou seja, pode haver pares de elementos para os quais nenhum elemento precede o outro no poset. Os pedidos parciais, portanto, generalizam os pedidos totais , nos quais cada par é comparável.

Definição informal

Uma ordem parcial define uma noção de comparação . Dois elementos x e y podem estar em qualquer uma das quatro relações mutuamente exclusivas entre si: ou x  <  y , ou x  =  y , ou x  >  y , ou x e y são incomparáveis .

Um conjunto com uma ordem parcial é chamado de conjunto parcialmente ordenado (também chamado de poset ). O termo conjunto ordenado também é usado às vezes, desde que fique claro a partir do contexto que nenhum outro tipo de ordem se refere. Em particular, conjuntos totalmente ordenados também podem ser referidos como "conjuntos ordenados", especialmente em áreas onde essas estruturas são mais comuns do que posets.

Um poset pode ser visualizado por meio de seu diagrama de Hasse , que representa a relação de ordenação.

Relação de ordem parcial

Uma relação de ordem parcial é uma relação homogénea que é transitória e anti-simétrico . Existem duas sub-definições comuns para uma relação de ordem parcial, para relações de ordem parcial reflexivas e irreflexivas, também chamadas de "não estritas" e "estritas", respectivamente. As duas definições podem ser colocadas em uma correspondência de um para um , portanto, para cada ordem parcial estrita, há uma única ordem parcial não estrita correspondente e vice-versa. O termo pedido parcial normalmente se refere a uma relação de pedido parcial não estrita.

Pedido parcial não estrito

Um reflexivo , fraco ou a ordem parcial não estrita é umarelação homogênea≤ sobre umconjunto que éreflexivo,antissimétricoetransitivo. Ou seja, para tudoisso deve satisfazer: ${\ displaystyle P}$${\ displaystyle a, b, c \ in P,}$

1. reflexividade : ou seja, cada elemento está relacionado a si mesmo.${\ displaystyle a \ leq a}$
2. antissimetria : se , ou seja, dois elementos distintos não precedem um ao outro.${\ displaystyle a \ leq b {\ text {e}} b \ leq a {\ text {then}} a = b}$
3. transitividade : se .${\ displaystyle a \ leq b {\ text {e}} b \ leq c {\ text {então}} a \ leq c}$

Uma ordem parcial não estrita também é conhecida como uma pré-ordem anti-simétrica .

Ordem parcial estrita

Um irreflexivo , forte ouordem parcial estrita emé uma relação homogênea <emque éirreflexiva,transitivaeassimétrica; ou seja, satisfaz as seguintes condições para todos${\ displaystyle P}$${\ displaystyle P}$${\ displaystyle a, b, c \ in P:}$

1. Irreflexividade : não , ou seja, nenhum elemento está relacionado a si mesmo${\ displaystyle a <a}$
2. Transitividade : se${\ displaystyle a <b {\ text {e}} b <c {\ text {então}} a <c,}$
3. Assimetria : se não .${\ displaystyle a <b}$${\ displaystyle b <a}$

A irreflexividade e a transitividade juntas implicam assimetria. Além disso, a assimetria implica irreflexividade. Em outras palavras, uma relação transitiva é assimétrica se e somente se for irreflexiva. Portanto, a definição é a mesma se omitir irreflexividade ou assimetria (mas não ambas).

Um pedido parcial estrito também é conhecido como pré-pedido estrito .

Correspondência de relações de ordem parcial estritas e não estritas

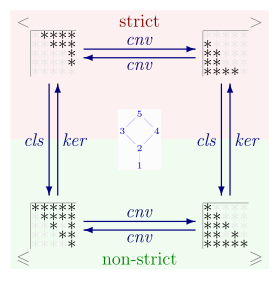
Ordens parciais estritas e não estritas em um conjunto estão intimamente relacionadas. Uma ordem parcial não-rígida pode ser convertida em uma ordem estrita parcial através da remoção de todas as relações de forma que é, a ordem estrita parcial é o conjunto que é a relação de identidade em e indica a subtracção conjunto . Inversamente, uma ordem parcial estrita <on pode ser convertida em uma ordem parcial não estrita juntando todos os relacionamentos dessa forma; ou seja, é uma ordem parcial não estrita. Assim, se for uma ordem parcial não estrita, então a ordem parcial estrita correspondente <é o kernel irreflexivo dado por ${\ displaystyle P}$${\ displaystyle \ leq}$${\ displaystyle a \ leq a;}$${\ displaystyle <\;: = \ \ leq \ \ setminus \ \ Delta _ {P}}$${\ displaystyle \ Delta _ {P}: = \ {(p, p): p \ in P \}}$${\ displaystyle P \ times P}$${\ displaystyle \; \ setminus \;}$${\ displaystyle P}$${\ displaystyle \ leq \;: = \; \ Delta _ {P} \; \ cup \; <\;}$${\ displaystyle \ leq}$

Por outro lado, se <é uma ordem parcial estrita, então a ordem parcial não estrita correspondente é o fechamento reflexivo dado por: ${\ displaystyle \ leq}$

$${\ displaystyle a \ leq b {\ text {if}} a <b {\ text {ou}} a = b.}$$

Pedidos duplos

Artigo principal: Dualidade (teoria da ordem)

O dual (ou oposto ) de uma relação de ordem parcial é definido deixando ser a

relação inversa de , isto é, se e somente se . O dual de uma ordem parcial não estrita é uma ordem parcial não estrita, e o dual de uma ordem parcial estrita é uma ordem parcial estrita. O dual de um dual de uma relação é a relação original. ${\ displaystyle (P, R ^ {\ text {op}})}$${\ displaystyle (P, R)}$${\ displaystyle R ^ {\ text {op}}}$${\ displaystyle R}$${\ displaystyle xR ^ {\ text {op}} y}$${\ displaystyle yRx}$

Notação

Podemos considerar um poset como um 3-tupla , ou mesmo 5-tupla , onde e são relações de ordem parcial não estrita e são relações de ordem parcial estrita, o dual de é , e e são igualmente duais um do outro. ${\ displaystyle (P, \ leq, <)}$${\ displaystyle (P, \ leq, <, \ geq,>)}$${\ displaystyle (P, \ leq)}$${\ displaystyle (P, \ geq)}$${\ displaystyle (P, <)}$${\ displaystyle (P,>)}$${\ displaystyle (P, \ geq)}$${\ displaystyle (P, \ leq)}$${\ displaystyle (P, <)}$${\ displaystyle (P,>)}$

Qualquer uma das quatro relações de ordem parcial em um determinado conjunto determina exclusivamente as outras três. Conseqüentemente, por uma questão de notação, podemos escrever ou , e assumir que as outras relações são definidas apropriadamente. A definição por meio de uma ordem parcial não estrita é mais comum. Alguns autores usam símbolos diferentes do que como ou distinguir ordens parciais de encomendas totais. ${\ displaystyle \ leq, <, \ geq, {\ text {e}}>}$${\ displaystyle (P, \ leq)}$${\ displaystyle (P, <)}$${\ displaystyle \ leq}$${\ displaystyle \ leq}$${\ displaystyle \ sqsubseteq}$${\ displaystyle \ preceq}$

Quando se referir a pedidos parciais, não deve ser tomado como

complemento de . é o inverso do kernel irreflexivo de , que é sempre um subconjunto do complemento de , mas é igual ao complemento de se, e somente se , é uma ordem total. ${\ displaystyle \ leq}$${\ displaystyle>}$${\ displaystyle>}$${\ displaystyle \ leq}$${\ displaystyle \ leq}$${\ displaystyle>}$${\ displaystyle \ leq}$ ${\ displaystyle \ leq}$

Exemplos

Exemplos padrão de posets que surgem em matemática incluem:

• Os números reais , ou em geral qualquer conjunto totalmente ordenado, ordenado pela relação padrão menor que ou igual ≤, é uma ordem parcial não estrita.
• Nos números reais, a relação usual de

menor que <é uma ordem parcial estrita e o mesmo também é verdadeiro para a relação usual de maior que > em${\ displaystyle P: = \ mathbb {R},}$${\ displaystyle \ mathbb {R}.}$

Por definição, toda ordem estrita fraca é uma ordem estrita parcial.

O conjunto de subconjuntos de um determinado conjunto (seu conjunto de potência ) ordenado por inclusão (ver Fig.1). Da mesma forma, o conjunto de sequências ordenadas por subsequência e o conjunto de strings ordenadas por substring .

O conjunto de números naturais equipados com a relação de divisibilidade .

O conjunto de vértices de um gráfico acíclico direcionado ordenado por alcançabilidade .

O conjunto de subespaços de um espaço vetorial ordenado por inclusão.

Para um conjunto P parcialmente ordenado , o espaço de sequência contendo todas as sequências de elementos de P , onde a sequência a precede a sequência b se cada item em a precede o item correspondente em b . Formalmente, se e somente se para todos ; ou seja, uma

ordem de componentes .${\ displaystyle \ left (a_ {n} \ right) _ {n \ in \ mathbb {N}} \ leq \ left (b_ {n} \ right) _ {n \ in \ mathbb {N}}}$${\ displaystyle a_ {n} \ leq b_ {n}}$${\ displaystyle n \ in \ mathbb {N}}$

Para um conjunto X e um conjunto parcialmente ordenado P , o espaço de funções contendo todas as funções de X a P , onde f ≤ g se e somente se f ( x ) ≤ g ( x ) para todos${\ displaystyle x \ in X.}$

Uma cerca , um conjunto parcialmente ordenado definido por uma sequência alternada de relações de ordem a < b > c < d ...

O conjunto de eventos em relatividade especial e, na maioria dos casos, a relatividade geral , onde por dois eventos X e Y , X ≤ Y se e somente se Y está no futuro cone de luz de X . Um evento Y só pode ser afectada por causalmente X se X ≤ Y .

Um exemplo familiar de um conjunto parcialmente ordenado é uma coleção de pessoas ordenadas por descendência genealógica . Alguns pares de pessoas mantêm a relação descendente-ancestral, mas outros pares de pessoas são incomparáveis, nenhum deles sendo descendente do outro.

Pedidos no produto cartesiano de conjuntos parcialmente pedidos

Fig.3 Ordem Lexicográfica em${\ displaystyle \ mathbb {N} \ times \ mathbb {N}}$

Fig.4 Pedido de produto em${\ displaystyle \ mathbb {N} \ times \ mathbb {N}}$

Fig.5 Fechamento reflexivo da ordem estrita do produto direto nos Elementos cobertos por (3,3) e cobrindo (3,3) são destacados em verde e vermelho, respectivamente.${\ displaystyle \ mathbb {N} \ times \ mathbb {N}.}$

Em ordem de força crescente, ou seja, conjuntos decrescentes de pares, três das possíveis ordens parciais no produto cartesiano de dois conjuntos parcialmente ordenados são (ver Fig.3-5):

• a ordem lexicográfica : ( a , b ) ≤ ( c , d ) se a < c ou ( a = c e b ≤ d );
• a ordem do

produto : ( a , b ) ≤ ( c , d ) se a ≤ c e b ≤ d ;

o fechamento reflexivo do produto direto das ordens estritas correspondentes: ( a , b ) ≤ ( c , d ) se ( a < c e b < d ) ou ( a = c e b = d ).

Todos os três podem ser definidos de forma semelhante para o produto cartesiano de mais de dois conjuntos.

Aplicado a espaços vetoriais ordenados no mesmo campo , o resultado é, em cada caso, também um espaço vetorial ordenado.

Veja também as encomendas do produto cartesiano de conjuntos totalmente encomendados .

Soma de conjuntos parcialmente ordenados

Outra forma de combinar dois posets (disjuntos) é a soma ordinal (ou soma linear ), Z = X ⊕ Y , definida na união dos conjuntos subjacentes X e Y pela ordem a ≤ _Z b se e somente se:

• a , b ∈ X com a ≤ _X b , ou
• a , b ∈ Y com a ≤ _Y b , ou
• um ∈ X e b ∈ Y .

Se dois posets forem bem ordenados , sua soma ordinal também será.

Ordens parciais série-paralela são formadas a partir da operação de soma ordinal (neste contexto, chamada de composição em série) e outra operação chamada de composição paralela. Composição paralela é a união disjunta de dois conjuntos parcialmente ordenados, sem relação de ordem entre os elementos de um conjunto e os elementos do outro conjunto.

Noções derivadas

Os exemplos usam o poset que consiste no

conjunto de todos os subconjuntos de um conjunto de três elementos ordenados por inclusão de conjunto (ver Fig.1). ${\ displaystyle ({\ mathcal {P}} (\ {x, y, z \}), \ subseteq)}$${\ displaystyle \ {x, y, z \},}$

• a está relacionado com b quando a ≤ b . Isso não implica que b também esteja relacionado a a , porque a relação não precisa ser simétrica . Por exemplo, está relacionado a, mas não o contrário.${\ displaystyle \ {x \}}$${\ displaystyle \ {x, y \},}$
• a e b são comparáveis se a ≤ b ou b ≤ a . Caso contrário, eles são incomparáveis . Por exemplo, e são comparáveis, enquanto e não são.${\ displaystyle \ {x \}}$${\ displaystyle \ {x, y, z \}}$${\ displaystyle \ {x \}}$${\ displaystyle \ {y \}}$
• Uma ordem total ou

ordem linear é uma ordem parcial sob a qual cada par de elementos é comparável, isto é, a tricotomia é válida. Por exemplo, os números naturais com sua ordem padrão.

Uma cadeia é um subconjunto de um poset que é um conjunto totalmente ordenado. Por exemplo, é uma cadeia.${\ displaystyle \ {\ {\, \}, \ {x \}, \ {x, y, z \} \}}$

Uma antichain é um subconjunto de um poset em que não há dois elementos distintos comparáveis. Por exemplo, o conjunto de singletons ${\ displaystyle \ {\ {x \}, \ {y \}, \ {z \} \}.}$

Um elemento de uma é dito ser estritamente inferior a um elemento b , se um ≤ b e Por exemplo, é estritamente inferior${\ displaystyle a \ neq b.}$${\ displaystyle \ {x \}}$${\ displaystyle \ {x, y \}.}$

Diz-se que um elemento a está coberto por outro elemento b , escrito a ⋖ b (ou a <: b ), se a for estritamente menor que be nenhum terceiro elemento c se encaixar entre eles; formalmente: se a ≤ b e forem verdadeiros, e a ≤ c ≤ b for falso para cada c com Usando a ordem estrita <, a relação a ⋖ b pode ser reformulada equivalentemente como " a < b, mas não a < c < b para qualquer c ". Por exemplo, é coberto por, mas não é coberto por${\ displaystyle a \ neq b}$${\ displaystyle a \ neq c \ neq b.}$${\ displaystyle \ {x \}}$${\ displaystyle \ {x, z \},}$${\ displaystyle \ {x, y, z \}.}$

Extrema

Existem várias noções de elemento "maior" e "menor" em um poset, notavelmente: ${\ displaystyle P,}$

• Maior elemento e menor elemento: Um elemento é o maior elemento se para cada elemento Um elemento é o menor elemento se para cada elemento Um poset só pode ter um maior ou menor elemento. Em nosso exemplo de execução, o conjunto é o maior elemento e o menor.${\ displaystyle g \ in P}$${\ displaystyle a \ in P, a \ leq g.}$${\ displaystyle m \ in P}$${\ displaystyle a \ in P, m \ leq a.}$${\ displaystyle \ {x, y, z \}}$${\ displaystyle \ {\, \}}$
• Elementos máximos e elementos mínimos: um elemento é um elemento máximo se não houver nenhum elemento tal que Da mesma forma, um elemento é um elemento mínimo se não houver nenhum elemento tal que se um poset tiver um elemento maior, deve ser o elemento máximo único, mas, caso contrário, pode haver mais de um elemento máximo e, da mesma forma, para elementos mínimos e elementos mínimos. Em nosso exemplo de execução, e são os elementos máximo e mínimo. Removendo-os, existem 3 elementos máximos e 3 elementos mínimos (ver Fig.6).${\ displaystyle g \ in P}$${\ displaystyle a \ in P}$${\ displaystyle a> g.}$${\ displaystyle m \ in P}$${\ displaystyle a \ in P}$${\ displaystyle a <m.}$${\ displaystyle \ {x, y, z \}}$${\ displaystyle \ {\, \}}$
• Limites superior e inferior : Para um subconjunto A de P , um elemento X em P é um limite superior de uma se uma  ≤  x , para cada elemento de um em um . Em particular, x não precisa de ser em um a ser um limite superior de uma . Da mesma forma, um elemento X em P é um limite inferior de A , se uma  ≥  x , para cada elemento de um em um . Uma maior elemento de P é um limite superior de P em si, e um elemento pelo menos é um limite inferior de P . Em nosso exemplo, o conjunto é um limite superior para a coleção de elementos${\ displaystyle \ {x, y \}}$${\ displaystyle \ {\ {x \}, \ {y \} \}.}$

Como outro exemplo, considere os inteiros positivos , ordenados por divisibilidade: 1 é o menor elemento, pois divide todos os outros elementos; por outro lado, este poset não tem um elemento maior (embora se alguém incluir 0 no poset, que é um múltiplo de qualquer inteiro, esse seria um elemento maior; consulte a Fig.7). Este conjunto parcialmente ordenado nem mesmo possui quaisquer elementos máximos, uma vez que qualquer g se divide por exemplo 2 g , que é distinto dele, então g não é máximo. Se o número 1 for excluído, mantendo a divisibilidade como ordenação dos elementos maior que 1, então o poset resultante não tem um elemento mínimo, mas qualquer número primo é um elemento mínimo para ele. Neste poset, 60 é um limite superior (embora não seja um limite superior) do subconjunto que não tem nenhum limite inferior (uma vez que 1 não está no poset); por outro lado, 2 é um limite inferior do subconjunto de potências de 2, que não possui nenhum limite superior. ${\ displaystyle \ {2,3,5,10 \},}$

Mapeamentos entre conjuntos parcialmente ordenados

Dados dois conjuntos parcialmente ordenados ( S , ≤) e ( T , ≼), uma função é chamada de preservação de ordem , ou monótona , ou isótona , se para todos implica f ( x ) ≼ f ( y ). Se ( U , ≲) também é um conjunto parcialmente ordenado e ambos e preservam a ordem, sua composição também preserva a ordem. Uma função é chamada de reflexão de ordem se para todo f ( x ) ≼ f ( y ) implica Se é tanto preservadora quanto refletora de ordem, então ela é chamada de incorporação de ordem de ( S , ≤) em ( T , ≼ ) Neste último caso, é necessariamente injetivo , uma vez que implica e por sua vez de acordo com o antisimetría de Se uma ordem-incorporação entre dois posets S e T existe, diz-se que S pode ser incorporado em T . Se uma incorporação de ordem é bijetiva , ela é chamada de isomorfismo de ordem , e as ordens parciais ( S , ≤) e ( T , ≼) são ditas isomórficas . As ordens isomórficas têm diagramas de Hasse estruturalmente semelhantes (ver Fig.8). Pode ser mostrado que se os mapas de preservação de ordem e existem de modo que e produzam a função de identidade em S e T , respectivamente, então S e T são isomórficos de ordem. ${\ displaystyle f: S \ to T}$${\ displaystyle x, y \ in S,}$ ${\ displaystyle x \ leq y}$${\ displaystyle f: S \ to T}$${\ displaystyle g: T \ to U}$ ${\ displaystyle g \ circ f: S \ to U}$${\ displaystyle f: S \ to T}$${\ displaystyle x, y \ in S,}$ ${\ displaystyle x \ leq y.}$${\ displaystyle f}$${\ displaystyle f}$${\ displaystyle f (x) = f (y)}$${\ displaystyle x \ leq y {\ text {e}} y \ leq x}$${\ displaystyle x = y}$${\ displaystyle \ leq.}$${\ displaystyle f: S \ to T}$${\ displaystyle f: S \ to T}$${\ displaystyle g: T \ to U}$${\ displaystyle g \ circ f}$${\ displaystyle f \ circ g}$

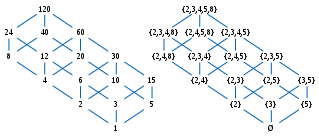
Por exemplo, um mapeamento do conjunto de números naturais (ordenados por divisibilidade) para o conjunto poderoso de números naturais (ordenados por inclusão de conjuntos) pode ser definido levando cada número ao conjunto de seus divisores primos . Ele preserva a ordem: se divide, então cada divisor primo de também é um divisor primo de No entanto, não é nem injetivo (uma vez que mapeia 12 e 6 para ) nem reflete a ordem (já que 12 não divide 6). Em vez disso, levar cada número para o conjunto de seus divisores de potência principais define um mapa que preserva e reflete a ordem e, portanto, embute a ordem. Não é um isomorfismo de ordem (uma vez que, por exemplo, não mapeia nenhum número para o conjunto ), mas pode ser feito restringindo seu codomorfismo à Fig.9 mostra um subconjunto de e sua imagem isomórfica sob a construção de tal isomorfismo de ordem em um conjunto de potência pode ser generalizado para uma ampla classe de ordens parciais, chamadas reticulados distributivos , veja " Teorema da representação de Birkhoff ". ${\ displaystyle f: \ mathbb {N} \ to \ mathbb {P} (\ mathbb {N})}$${\ displaystyle x}$${\ displaystyle y,}$${\ displaystyle x}$${\ displaystyle y.}$${\ displaystyle \ {2,3 \}}$${\ displaystyle g: \ mathbb {N} \ to \ mathbb {P} (\ mathbb {N})}$${\ displaystyle \ {4 \}}$${\ displaystyle g (\ mathbb {N}).}$${\ displaystyle \ mathbb {N}}$${\ displaystyle g.}$

Número de pedidos parciais

A sequência A001035 em OEIS fornece o número de pedidos parciais em um conjunto de n elementos rotulados:

Número de relações binárias de n elementos de diferentes tipos

Elementos	Algum	Transitivo	Reflexivo	Pedido antecipado	Pedido parcial	Pré-encomenda total	Ordem total	Relação de equivalência
0	1	1	1	1	1	1	1	1
1	2	2	1	1	1	1	1	1
2	16	13	4	4	3	3	2	2
3	512	171	64	29	19	13	6	5
4	65.536	3.994	4.096	355	219	75	24	15
n	2 n 2		2 n 2 - n			${\ textstyle \ sum _ {k = 0} ^ {n} k!}$S ( n , k )	n !	${\ textstyle \ sum _ {k = 0} ^ {n}}$S ( n , k )
OEIS	A002416	A006905	A053763	A000798	A001035	A000670	A000142	A000110

O número de pedidos parciais estritos é igual ao de pedidos parciais.

Se a contagem for feita apenas até o isomorfismo, obtém-se a sequência 1, 1, 2, 5, 16, 63, 318, ... (sequência A000112 no OEIS ).

Extensão linear

Uma ordem parcial em um conjunto é uma extensão de outra ordem parcial em, desde que, para todos os elementos, sempre que também for o caso de Uma extensão linear é uma extensão que também é uma ordem linear (ou seja, total). Como um exemplo clássico, a ordem lexicográfica de conjuntos totalmente ordenados é uma extensão linear de sua ordem de produto. Cada pedido parcial pode ser estendido para um pedido total ( princípio de extensão do pedido ). ${\ displaystyle \ leq ^ {*}}$${\ displaystyle X}$${\ displaystyle \ leq}$${\ displaystyle X}$${\ displaystyle x, y \ in X,}$${\ displaystyle x \ leq y,}$${\ displaystyle x \ leq ^ {*} y.}$

Na ciência da computação , os algoritmos para encontrar extensões lineares de ordens parciais (representadas como ordens de alcançabilidade de gráficos acíclicos direcionados ) são chamados de classificação topológica .

Gráficos acíclicos direcionados

Ordens parciais estritas correspondem diretamente a gráficos acíclicos direcionados (DAGs). Se um gráfico for construído tomando cada elemento de como um nó e cada elemento de como uma borda, então cada ordem parcial estrita é um DAG, e o fechamento transitivo de um DAG é tanto uma ordem parcial estrita quanto um DAG em si . Em contraste, uma ordem parcial não estrita teria auto-loops em cada nó e, portanto, não seria um DAG. ${\ displaystyle P}$${\ displaystyle \ leq}$

Na teoria da categoria

Cada poset (e cada conjunto pré- ordenado ) pode ser considerado como uma categoria onde, para objetos e há no máximo um morfismo de a Mais explicitamente, seja hom ( x , y ) = {( x , y )} se x ≤ y ( e, caso contrário, o conjunto vazio) e Tais categorias às vezes são chamadas de posetal . ${\ displaystyle x}$${\ displaystyle y,}$${\ displaystyle x}$${\ displaystyle y.}$${\ displaystyle (y, z) \ circ (x, y) = (x, z).}$

Posets são equivalentes entre si se e somente se forem isomórficos . Em um poset, o menor elemento, se existir, é um objeto inicial , e o maior elemento, se existir, é um objeto terminal . Além disso, cada conjunto pré-encomendado é equivalente a um poset. Finalmente, cada subcategoria de um poset é fechada por isomorfismo .

Ordens parciais em espaços topológicos

Se for um conjunto parcialmente ordenado que também recebeu a estrutura de um espaço topológico , então é costume assumir que é um subconjunto fechado do espaço do produto topológico. Sob essa suposição, as relações de ordem parcial são bem comportadas em limites no sentido de que se e para todos então${\ displaystyle P}$${\ displaystyle \ {(a, b): a \ leq b \}}$ ${\ displaystyle P \ times P.}$${\ displaystyle a_ {i} \ para a,}$${\ displaystyle b_ {i} \ para b,}$${\ displaystyle i}$ ${\ displaystyle a_ {i} \ leq b_ {i},}$${\ displaystyle a \ leq b.}$

Intervalos

Um intervalo de poset P é um subconjunto I de P com a propriedade de que, para qualquer x e y em I e qualquer Z em P , se x ≤ z ≤ y , então Z também é em I . (Esta definição generaliza a definição de intervalo para números reais.)

Para a ≤ b , o intervalo fechado [ a , b ] é o conjunto de elementos x que satisfazem a ≤ x ≤ b (ou seja, a ≤ x e x ≤ b ). Ele contém pelo menos os elementos a e b .

Usando a relação estrita correspondente "<", o intervalo aberto ( a , b ) é o conjunto de elementos x satisfazendo a < x < b (ou seja, a < x e x < b ). Um intervalo aberto pode estar vazio mesmo se a < b . Por exemplo, o intervalo aberto (1, 2) nos inteiros está vazio, pois não há inteiros I tais que 1 < I <2 .

Os intervalos semiabertos [ a , b ) e ( a , b ] são definidos de forma semelhante.

Às vezes, as definições são estendidas para permitir a > b , caso em que o intervalo está vazio.

Um intervalo I é limitado se existirem elementos tais que I ⊆ [ a , b ] . Cada intervalo que pode ser representado na notação de intervalo é obviamente limitado, mas o inverso não é verdadeiro. Por exemplo, seja P = (0, 1) ∪ (1, 2) ∪ (2, 3) como um subposet dos números reais . O subconjunto (1, 2) é um intervalo limitado, mas não tem nenhum ínfimo ou supremum em P , de modo que não pode ser escrito em notação intervalo usando elementos de P . ${\ displaystyle a, b \ in P}$

Um poset é denominado localmente finito se cada intervalo limitado for finito. Por exemplo, os inteiros são localmente finitos sob sua ordem natural. A ordem lexicográfica no produto cartesiano não é localmente finita, uma vez que (1, 2) ≤ (1, 3) ≤ (1, 4) ≤ (1, 5) ≤ ... ≤ (2, 1) . Usando a notação de intervalo, a propriedade " a é coberto por b " pode ser reformulada equivalentemente como${\ displaystyle \ mathbb {N} \ times \ mathbb {N}}$${\ displaystyle [a, b] = \ {a, b \}.}$

Este conceito de um intervalo em uma ordem parcial não deve ser confundido com a classe particular de ordens parciais conhecidas como ordens de intervalo .

Veja também

Notas

Citações

Referências

• Davey, BA; Priestley, HA (2002). Introdução a Lattices and Order (2ª ed.). Nova York: Cambridge University Press. ISBN 978-0-521-78451-1.
• Deshpande, Jayant V. (1968). “Sobre a continuidade de uma ordem parcial” . Proceedings of the American Mathematical Society . 19 (2): 383–386. doi : 10.1090 / S0002-9939-1968-0236071-7 .
• Schmidt, Gunther (2010). Matemática Relacional . Enciclopédia de Matemática e suas Aplicações. 132 . Cambridge University Press. ISBN 978-0-521-76268-7.
• Bernd Schröder (11 de maio de 2016). Conjuntos ordenados: uma introdução com conexões de Combinatorics para topologia . Birkhäuser. ISBN 978-3-319-29788-0.
• Stanley, Richard P. (1997). Combinatória enumerativa 1 . Cambridge Studies in Advanced Mathematics. 49 . Cambridge University Press. ISBN 0-521-66351-2.

links externos

• Sequência OEIS A001035 (Número de posets com n elementos rotulados)
• Sequência OEIS A000112 (Número de conjuntos parcialmente ordenados ("posets") com n elementos não rotulados.)