Formulação integral de caminho - Path integral formulation

Parte de uma série de artigos sobre
Mecânica quântica
${\ displaystyle i \ hbar {\ frac {\ partial} {\ partial t}} | \ psi (t) \ rangle = {\ hat {H}} | \ psi (t) \ rangle}$ Equação de Schrödinger
Introdução Glossário História
Fundo Mecânica clássica Velha teoria quântica Notação de sutiã Hamiltoniano Interferência
Fundamentos Complementaridade Decoerência Emaranhamento Nível de energia Medição Não localidade Número quântico Estado Sobreposição Simetria Tunelamento Incerteza Função de onda  ( recolher )
Experimentos Desigualdade de Bell Davisson – Germer Fenda dupla Elitzur-Vaidman Franck – Hertz Desigualdade de Leggett-Garg Mach – Zehnder Popper Borracha quântica  ( escolha retardada ) gato de Schrodinger Stern – Gerlach Escolha atrasada de Wheeler
Formulações Visão geral Heisenberg Interação Matriz Espaço de fase Schrödinger Soma sobre histórias (integral do caminho)
Equações Dirac Klein – Gordon Pauli Rydberg Schrödinger
Interpretações Visão geral Bayesiano Histórias consistentes Copenhague de Broglie – Bohm Conjunto Variável oculta Muitos mundos Colapso objetivo Lógica quântica Relacional Transacional
Tópicos avançados Mecânica quântica relativística Teoria quântica de campos Ciência da informação quântica Computação quântica Caos quântico Matriz de densidade Teoria de dispersão Mecânica estatística quântica Aprendizado de máquina quântico
Cientistas Aharonov Sino Blackett Bloch Bohm Bohr Nascer Bose de Broglie Candlin Compton Dirac Davisson Debye Ehrenfest Einstein Everett Fock Fermi Feynman Glauber Gutzwiller Heisenberg Hilbert Jordânia Kramers Pauli Cordeiro Landau Laue Moseley Millikan Onnes Planck Rabi Raman Rydberg Schrödinger Sommerfeld von Neumann Weyl Wien Wigner Zeeman Zeilinger
v t e

A formulação da integral de caminho é uma descrição em mecânica quântica que generaliza o princípio de ação da mecânica clássica . Ele substitui a noção clássica de uma trajetória clássica única e única para um sistema com uma soma, ou integral funcional , ao longo de uma infinidade de trajetórias possíveis mecanicamente quânticas para calcular uma amplitude quântica .

Esta formulação provou ser crucial para o desenvolvimento subsequente da física teórica , porque a covariância de Lorentz manifesta (componentes de tempo e espaço das quantidades entram nas equações da mesma maneira) é mais fácil de alcançar do que no formalismo de operador da quantização canônica . Ao contrário dos métodos anteriores, a integral de caminho permite alterar facilmente as coordenadas entre descrições canônicas muito diferentes do mesmo sistema quântico. Outra vantagem é que é na prática mais fácil adivinhar a forma correta da Lagrangiana de uma teoria, que entra naturalmente nas integrais de caminho (para interações de um certo tipo, estas são coordenadas espaciais ou integrais de caminho de Feynman ), do que a hamiltoniana . Possíveis desvantagens da abordagem incluem que a unidade (isso está relacionado à conservação da probabilidade; as probabilidades de todos os resultados fisicamente possíveis devem somar um) da matriz S é obscura na formulação. A abordagem da integral do caminho provou ser equivalente aos outros formalismos da mecânica quântica e da teoria quântica de campos. Assim, ao derivar uma das abordagens da outra, os problemas associados a uma ou outra abordagem (conforme exemplificado pela covariância ou unitariedade de Lorentz) desaparecem.

A integral de caminho também relaciona processos quânticos e estocásticos , e isso forneceu a base para a grande síntese da década de 1970, que unificou a teoria quântica de campos com a teoria estatística de campos de um campo flutuante próximo a uma transição de fase de segunda ordem . A equação de Schrödinger é uma equação de difusão com uma constante de difusão imaginária, e a integral de caminho é uma continuação analítica de um método para somar todos os passeios aleatórios possíveis .

A ideia básica da formulação da integral de caminho pode ser rastreada até Norbert Wiener , que introduziu a integral de Wiener para resolver problemas em difusão e movimento browniano . Essa ideia foi estendida ao uso do Lagrangiano na mecânica quântica por Paul Dirac em seu artigo de 1933. O método completo foi desenvolvido em 1948 por Richard Feynman . Algumas preliminares foram elaboradas no início de seu trabalho de doutorado, sob a supervisão de John Archibald Wheeler . A motivação original originou-se do desejo de obter uma formulação da mecânica quântica para a teoria do absorvedor de Wheeler-Feynman usando um Lagrangiano (em vez de um Hamiltoniano ) como ponto de partida.

Princípio de ação quântica

Na mecânica quântica, como na mecânica clássica, o hamiltoniano é o gerador das traduções de tempo. Isso significa que o estado em um momento ligeiramente posterior difere do estado no momento atual pelo resultado de agir com o operador hamiltoniano (multiplicado pela unidade imaginária negativa , - i ). Para estados com uma energia definida, esta é uma declaração da relação de De Broglie entre frequência e energia, e a relação geral é consistente com isso mais o princípio de superposição .

O hamiltoniano na mecânica clássica é derivado de um lagrangiano , que é uma quantidade mais fundamental em relação à relatividade especial . O hamiltoniano indica como avançar no tempo, mas o tempo é diferente em diferentes referenciais . O Lagrangiano é um escalar de Lorentz , enquanto o Hamiltoniano é o componente de tempo de um quatro vetores . Portanto, o hamiltoniano é diferente em quadros diferentes, e esse tipo de simetria não é aparente na formulação original da mecânica quântica.

O hamiltoniano é uma função da posição e do momento ao mesmo tempo, e determina a posição e o momento um pouco mais tarde. O Lagrangiano é uma função da posição agora e da posição um pouco mais tarde (ou, equivalentemente para separações de tempo infinitesimais, é uma função da posição e da velocidade). A relação entre os dois é por uma transformação de Legendre , e a condição que determina as equações clássicas de movimento (as equações de Euler-Lagrange ) é que a ação tem um extremo.

Na mecânica quântica, a transformada de Legendre é difícil de interpretar, porque o movimento não segue uma trajetória definida. Na mecânica clássica, com discretização no tempo, a transformada de Legendre torna-se

${\ displaystyle \ varepsilon H = p (t) {\ big (} q (t + \ varejpsilon) -q (t) {\ big)} - \ varejpsilon L}$

e

${\ displaystyle p = {\ frac {\ partial L} {\ partial {\ dot {q}}}},}$

onde a derivada parcial em relação a mantém q ( t + ε ) fixo. A transformação inversa de Legendre é ${\ displaystyle {\ dot {q}}}$

${\ displaystyle \ varepsilon L = \ varepsilon p {\ dot {q}} - \ varepsilon H,}$

Onde

${\ displaystyle {\ dot {q}} = {\ frac {\ parcial H} {\ parcial p}},}$

e a derivada parcial agora é em relação a p em q fixo .

Em mecânica quântica, o estado é uma superposição de diferentes estados com diferentes valores de Q , ou diferentes valores de p , e a quantidade p e q podem ser interpretados como noncommuting operadores. O operador p só é definido em estados que são indefinidos em relação a q . Portanto, considere dois estados separados no tempo e aja com o operador correspondente ao Lagrangiano:

${\ displaystyle e ^ {i {\ big [} p {\ big (} q (t + \ varepsilon) -q (t) {\ big)} - \ varejpsilon H (p, q) {\ big]}}. }$

Se as multiplicações implícitas nesta fórmula são reinterpretadas como multiplicações de matrizes , o primeiro fator é

${\ displaystyle e ^ {- ipq (t)},}$

e se isso também for interpretado como uma multiplicação de matriz, a soma de todos os estados integra-se a todos os q ( t ) e, portanto, é necessária a transformada de Fourier em q ( t ) para mudar a base para p ( t ) . Essa é a ação no espaço de Hilbert - base de mudança para p no tempo t .

A seguir vem

${\ displaystyle e ^ {- i \ varepsilon H (p, q)},}$

ou evoluir um tempo infinitesimal no futuro .

Finalmente, o último fator nesta interpretação é

${\ displaystyle e ^ {ipq (t + \ varepsilon)},}$

o que significa mudar a base de volta para q posteriormente .

Isso não é muito diferente da evolução temporal comum: o fator H contém todas as informações dinâmicas - ele empurra o estado para frente no tempo. A primeira parte e a última parte são apenas transformadas de Fourier para mudar para uma base q pura a partir de uma base p intermediária .

Outra forma de dizer isto é que uma vez que o hamiltoniano é naturalmente uma função de p e q , exponencializando esta quantidade e mudando base de p para q em cada passo permite que o elemento de matriz de H para ser expressa como uma função simples ao longo de cada trajecto. Esta função é o análogo quântico da ação clássica. Essa observação se deve a Paul Dirac .

Dirac observou ainda que pode-se enquadrar o operador de evolução de tempo na representação S :

${\ displaystyle e ^ {i \ varepsilon S},}$

e isso dá o operador de evolução no tempo entre o tempo t e o tempo t + 2 ε . Enquanto na representação H a quantidade que está sendo somada nos estados intermediários é um elemento obscuro da matriz, na representação S ela é reinterpretada como uma quantidade associada ao caminho. No limite em que se toma uma grande potência desse operador, reconstrói-se a evolução quântica completa entre dois estados, o primeiro com valor fixo de q (0) e o último com valor fixo de q ( t ) . O resultado é uma soma de caminhos com uma fase, que é a ação quântica. Crucialmente, Dirac identificou neste artigo a razão mecânica quântica profunda para o princípio da ação mínima controlando o limite clássico (ver caixa de cotação).

Interpretação de Feynman

O trabalho de Dirac não forneceu uma prescrição precisa para calcular a soma dos caminhos, e ele não mostrou que se pudesse recuperar a equação de Schrödinger ou as relações de comutação canônicas a partir dessa regra. Isso foi feito por Feynman. Ou seja, o caminho clássico surge naturalmente no limite clássico.

Feynman mostrou que a ação quântica de Dirac era, para a maioria dos casos de interesse, simplesmente igual à ação clássica, apropriadamente discretizada. Isso significa que a ação clássica é a fase adquirida pela evolução quântica entre dois pontos finais fixos. Ele propôs recuperar toda a mecânica quântica dos seguintes postulados:

1. A probabilidade de um evento é dada pelo módulo ao quadrado de um número complexo denominado "amplitude de probabilidade".
2. A amplitude da probabilidade é dada pela soma das contribuições de todos os caminhos no espaço de configuração.
3. A contribuição de um caminho é proporcional a e ^{iS / ħ} , onde S é a ação dada pela integral de tempo da Lagrangiana ao longo do caminho.

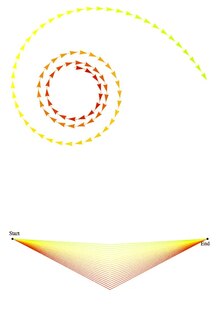
A fim de encontrar a amplitude de probabilidade geral para um determinado processo, então, adiciona-se, ou integra , a amplitude do 3º postulado sobre o espaço de todos os caminhos possíveis do sistema entre os estados inicial e final, incluindo aqueles que são absurdo para os padrões clássicos. No cálculo da amplitude de probabilidade para uma única partícula para ir de um espaço de tempo de coordenadas para outro, é correcto incluir caminhos em que a partícula descreve elaborados curlicues , curvas em que os rebentos de partículas fora para o espaço exterior e moscas de volta novamente, e assim por diante. A integral de caminho atribui a todas essas amplitudes peso igual, mas fase variável , ou argumento do número complexo . Contribuições de caminhos totalmente diferentes da trajetória clássica podem ser suprimidas por interferência (veja abaixo).

Feynman mostrou que esta formulação da mecânica quântica é equivalente à abordagem canônica da mecânica quântica quando o hamiltoniano é no máximo quadrático no momento. Uma amplitude calculada de acordo com os princípios de Feynman também obedecerá à equação de Schrödinger para o hamiltoniano correspondente à ação dada.

A formulação integral do caminho da teoria quântica de campos representa a amplitude de transição (correspondendo à função de correlação clássica ) como uma soma ponderada de todas as histórias possíveis do sistema do estado inicial ao final. Um diagrama de Feynman é uma representação gráfica de uma contribuição perturbativa para a amplitude de transição.

Integral de caminho na mecânica quântica

Derivação de divisão de tempo

Uma abordagem comum para derivar a fórmula integral do caminho é dividir o intervalo de tempo em pequenas partes. Feito isso, a fórmula do produto Trotter nos diz que a não comutatividade dos operadores de energia cinética e potencial pode ser ignorada.

Para uma partícula em um potencial suave, a integral de caminho é aproximada por caminhos em zigue-zague , que em uma dimensão é um produto de integrais comuns. Para o movimento da partícula da posição x _a no tempo t _a até x _b no tempo t _b , a sequência de tempo

${\ displaystyle t_ {a} = t_ {0} <t_ {1} <\ cdots <t_ {n-1} <t_ {n} <t_ {n + 1} = t_ {b}}$

pode ser dividido em n + 1 segmentos menores t _j - t _{j - 1} , onde j = 1, ..., n + 1 , de duração fixa

${\ displaystyle \ varepsilon = \ Delta t = {\ frac {t_ {b} -t_ {a}} {n + 1}}.}$

Esse processo é chamado de divisão de tempo .

Uma aproximação para a integral do caminho pode ser calculada como proporcional a

${\ displaystyle \ int \ limits _ {- \ infty} ^ {+ \ infty} \ cdots \ int \ limits _ {- \ infty} ^ {+ \ infty} \ exp \ left ({\ frac {i} {\ hbar}} \ int _ {t_ {a}} ^ {t_ {b}} L {\ big (} x (t), v (t) {\ big)} \, dt \ right) \, dx_ {0 } \, \ cdots \, dx_ {n},}$

onde L ( x , v ) é o Lagrangiano do sistema unidimensional com variável de posição x ( t ) e velocidade v = ẋ ( t ) considerada (veja abaixo), e dx _j corresponde à posição no j- ésimo intervalo de tempo , se a integral de tempo for aproximada por uma soma de n termos.

No limite n → ∞ , este torna-se um integrante funcional , que, para além de um factor não essencial, é directamente o produto da probabilidade amplitudes ⟨ x _b , t _b | x _um , t _um ⟩ (mais precisamente, uma vez que um trabalho mosto com um espectro contínuo, as respectivas densidades) para encontrar a partícula mecânica quântica em t _uma no estado inicial x _um e a t _b no estado final x _b .

Na verdade, L é o Lagrangiano clássico do sistema unidimensional considerado,

${\ displaystyle L (x, {\ dot {x}}) = TV = {\ frac {1} {2}} m | {\ dot {x}} | ^ {2} -V (x)}$

e o referido "ziguezague" corresponde ao aparecimento dos termos

${\ displaystyle \ exp \ left ({\ frac {i} {\ hbar}} \ varepsilon \ sum _ {j = 1} ^ {n + 1} L \ left ({\ tilde {x}} _ {j} , {\ frac {x_ {j} -x_ {j-1}} {\ varepsilon}}, j \ right) \ right)}$

na soma de Riemann aproximando a integral de tempo, que são finalmente integrados sobre x ₁ a x _n com a medida de integração dx ₁ ... dx _n , x̃ _j é um valor arbitrário do intervalo correspondente a j , por exemplo, seu centro, x _j + x _{j −1}/2.

Assim, em contraste com a mecânica clássica, não apenas o caminho estacionário contribui, mas na verdade todos os caminhos virtuais entre o ponto inicial e o ponto final também contribuem.

Integral do caminho

Em termos da função de onda na representação da posição, a fórmula integral do caminho é a seguinte:

${\ displaystyle \ psi (x, t) = {\ frac {1} {Z}} \ int _ {\ mathbf {x} (0) = x} {\ mathcal {D}} \ mathbf {x} \, e ^ {iS [\ mathbf {x}, {\ dot {\ mathbf {x}}}]} \ psi _ {0} (\ mathbf {x} (t)) \,}$

onde denota integração em todos os caminhos com e onde é um fator de normalização. Aqui está a ação, dada por ${\ displaystyle {\ mathcal {D}} \ mathbf {x}}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {x} (0) = x}$${\ displaystyle Z}$${\ displaystyle S}$

${\ displaystyle S [\ mathbf {x}, {\ dot {\ mathbf {x}}}] = \ int dt \, L (\ mathbf {x} (t), {\ dot {\ mathbf {x}} } (t))}$

Partícula livre

A representação integral do caminho fornece a amplitude quântica para ir do ponto x ao ponto y como uma integral sobre todos os caminhos. Para uma ação de partícula livre (por simplicidade, deixe m = 1 , ħ = 1 )

${\ displaystyle S = \ int {\ frac {{\ dot {x}} ^ {2}} {2}} \, dt,}$

a integral pode ser avaliada explicitamente.

Para fazer isso, é conveniente começar sem o fator i no exponencial, de modo que grandes desvios sejam suprimidos por pequenos números, e não pelo cancelamento das contribuições oscilatórias. A amplitude (ou kernel) lê:

${\ displaystyle K (xy; T) = \ int _ {x (0) = x} ^ {x (T) = y} \ exp \ left (- \ int _ {0} ^ {T} {\ frac { {\ dot {x}} ^ {2}} {2}} \, dt \ right) \, Dx.}$

Dividindo a integral em fatias de tempo:

${\ displaystyle K (x, y; T) = \ int _ {x (0) = x} ^ {x (T) = y} \ prod _ {t} \ exp \ left (- {\ tfrac {1} {2}} \ left ({\ frac {x (t + \ varepsilon) -x (t)} {\ varepsilon}} \ right) ^ {2} \ varepsilon \ right) \, Dx,}$

onde o Dx é interpretado como uma coleção finita de integrações em cada múltiplo inteiro de ε . Cada fator no produto é gaussiano em função de x ( t + ε ) centrado em x ( t ) com variância ε . As integrais múltiplas são uma convolução repetida deste G _ε gaussiano com cópias de si mesmo em tempos adjacentes:

${\ displaystyle K (xy; T) = G _ {\ varejpsilon} * G _ {\ varejpsilon} * \ cdots * G _ {\ varejpsilon},}$

onde o número de convoluções é T/ε. O resultado é fácil de avaliar tomando a transformada de Fourier de ambos os lados, de modo que as convoluções se tornem multiplicações:

${\ displaystyle {\ tilde {K}} (p; T) = {\ tilde {G}} _ {\ varejpsilon} (p) ^ {T / \ varejpsilon}.}$

A transformada de Fourier do G gaussiano é outra gaussiana de variação recíproca:

${\ displaystyle {\ tilde {G}} _ {\ varepsilon} (p) = e ^ {- {\ frac {\ varepsilon p ^ {2}} {2}}},}$

e o resultado é

${\ displaystyle {\ tilde {K}} (p; T) = e ^ {- {\ frac {Tp ^ {2}} {2}}}.}$

A transformada de Fourier dá K , e é gaussiana novamente com variância recíproca:

${\ displaystyle K (xy; T) \ propto e ^ {- {\ frac {(xy) ^ {2}} {2T}}}.}$

A constante de proporcionalidade não é realmente determinada pela abordagem de divisão de tempo, apenas a proporção de valores para diferentes opções de endpoint é determinada. A constante de proporcionalidade deve ser escolhida para garantir que entre cada duas fatias de tempo a evolução do tempo seja quântica-mecanicamente unitária, mas uma maneira mais esclarecedora de corrigir a normalização é considerar a integral de caminho como uma descrição de um processo estocástico.

O resultado tem uma interpretação de probabilidade. A soma de todos os caminhos do fator exponencial pode ser vista como a soma de cada caminho da probabilidade de selecionar esse caminho. A probabilidade é o produto sobre cada segmento da probabilidade de selecionar aquele segmento, de modo que cada segmento seja escolhido de forma probabilística de forma independente. O fato de a resposta ser uma Gaussiana se espalhando linearmente no tempo é o teorema do limite central , que pode ser interpretado como a primeira avaliação histórica de uma integral de caminho estatístico.

A interpretação da probabilidade dá uma escolha natural de normalização. A integral do caminho deve ser definida de modo que

${\ displaystyle \ int K (xy; T) \, dy = 1.}$

Esta condição normaliza a Gaussiana e produz um kernel que obedece à equação de difusão:

${\ displaystyle {\ frac {d} {dt}} K (x; T) = {\ frac {\ nabla ^ {2}} {2}} K.}$

Para integrais de caminho oscilatório, aqueles com um i no numerador, o fatiamento de tempo produz gaussianas convolvidas, assim como antes. Agora, entretanto, o produto da convolução é marginalmente singular, uma vez que requer limites cuidadosos para avaliar as integrais oscilantes. Para tornar os fatores bem definidos, a maneira mais fácil é adicionar uma pequena parte imaginária ao incremento de tempo ε . Isso está intimamente relacionado à rotação de Wick . Então, o mesmo argumento de convolução de antes fornece o kernel de propagação:

${\ displaystyle K (xy; T) \ propto e ^ {\ frac {i (xy) ^ {2}} {2T}},}$

que, com a mesma normalização de antes (não a normalização por soma dos quadrados - esta função tem uma norma divergente), obedece a uma equação de Schrödinger livre:

${\ displaystyle {\ frac {d} {dt}} K (x; T) = i {\ frac {\ nabla ^ {2}} {2}} K.}$

Isso significa que qualquer superposição de K s também obedecerá à mesma equação, por linearidade. Definindo

${\ displaystyle \ psi _ {t} (y) = \ int \ psi _ {0} (x) K (xy; t) \, dx = \ int \ psi _ {0} (x) \ int _ {x (0) = x} ^ {x (t) = y} e ^ {iS} \, Dx,}$

então ψ _t obedece a equação de Schrödinger livre assim como K faz:

${\ displaystyle i {\ frac {\ partial} {\ partial t}} \ psi _ {t} = - {\ frac {\ nabla ^ {2}} {2}} \ psi _ {t}.}$

Oscilador harmônico simples

O Lagrangiano para o oscilador harmônico simples é

${\ displaystyle {\ mathcal {L}} = {\ tfrac {1} {2}} m {\ dot {x}} ^ {2} - {\ tfrac {1} {2}} m \ omega ^ {2 } x ^ {2}.}$

Escreva sua trajetória x ( t ) como a trajetória clássica mais alguma perturbação, x ( t ) = x _c ( t ) + δx ( t ) e a ação como S = S _c + δS . A trajetória clássica pode ser escrita como

${\ displaystyle x _ {\ text {c}} (t) = x_ {i} {\ frac {\ sin \ omega (t_ {f} -t)} {\ sin \ omega (t_ {f} -t_ {i })}} + x_ {f} {\ frac {\ sin \ omega (t-t_ {i})} {\ sin \ omega (t_ {f} -t_ {i})}}.}$

Esta trajetória produz a ação clássica

${\ displaystyle {\ begin {alinhados} S _ {\ text {c}} & = \ int _ {t_ {i}} ^ {t_ {f}} {\ mathcal {L}} \, dt = \ int _ { t_ {i}} ^ {t_ {f}} \ left ({\ tfrac {1} {2}} m {\ dot {x}} ^ {2} - {\ tfrac {1} {2}} m \ omega ^ {2} x ^ {2} \ right) \, dt \\ [6pt] & = {\ frac {1} {2}} m \ omega \ left ({\ frac {(x_ {i} ^ { 2} + x_ {f} ^ {2}) \ cos \ omega (t_ {f} -t_ {i}) - 2x_ {i} x_ {f}} {\ sin \ omega (t_ {f} -t_ { i})}} \ direita) ~. \ end {alinhado}}}$

Em seguida, expanda o desvio do caminho clássico como uma série de Fourier e calcule a contribuição para a ação δS , que dá

${\ displaystyle S = S _ {\ text {c}} + \ sum _ {n = 1} ^ {\ infty} {\ tfrac {1} {2}} a_ {n} ^ {2} {\ frac {m } {2}} \ left ({\ frac {(n \ pi) ^ {2}} {t_ {f} -t_ {i}}} - \ omega ^ {2} (t_ {f} -t_ {i })\direito).}$

Isso significa que o propagador é

${\ displaystyle {\ begin {alinhados} K (x_ {f}, t_ {f}; x_ {i}, t_ {i}) & = Qe ^ {\ frac {iS _ {\ text {c}}} {\ hbar}} \ prod _ {j = 1} ^ {\ infty} {\ frac {j \ pi} {\ sqrt {2}}} \ int da_ {j} \ exp {\ left ({\ frac {i} {2 \ hbar}} a_ {j} ^ {2} {\ frac {m} {2}} \ left ({\ frac {(j \ pi) ^ {2}} {t_ {f} -t_ {i }}} - \ omega ^ {2} (t_ {f} -t_ {i}) \ right) \ right)} \\ [6pt] & = e ^ {\ frac {iS _ {\ text {c}}} {\ hbar}} Q \ prod _ {j = 1} ^ {\ infty} \ left (1- \ left ({\ frac {\ omega (t_ {f} -t_ {i})} {j \ pi} } \ right) ^ {2} \ right) ^ {- {\ frac {1} {2}}} \ end {alinhado}}}$

para alguma normalização

${\ displaystyle Q = {\ sqrt {\ frac {m} {2 \ pi i \ hbar (t_ {f} -t_ {i})}}} ~.}$

Usando a representação de produto infinito da função sinc ,

${\ displaystyle \ prod _ {j = 1} ^ {\ infty} \ left (1 - {\ frac {x ^ {2}} {j ^ {2}}} \ right) = {\ frac {\ sin \ pi x} {\ pi x}},}$

o propagador pode ser escrito como

${\ displaystyle K (x_ {f}, t_ {f}; x_ {i}, t_ {i}) = Qe ^ {\ frac {iS _ {\ text {c}}} {\ hbar}} {\ sqrt { \ frac {\ omega (t_ {f} -t_ {i})} {\ sin \ omega (t_ {f} -t_ {i})}}} = e ^ {\ frac {iS_ {c}} {\ hbar}} {\ sqrt {\ frac {m \ omega} {2 \ pi i \ hbar \ sin \ omega (t_ {f} -t_ {i})}}}.}$

Seja T = t _f - t _i . Pode-se escrever este propagador em termos de autoestados de energia como

${\ displaystyle {\ begin {alinhados} K (x_ {f}, t_ {f}; x_ {i}, t_ {i}) & = \ left ({\ frac {m \ omega} {2 \ pi i \ hbar \ sin \ omega T}} \ right) ^ {\ frac {1} {2}} \ exp {\ left ({\ frac {i} {\ hbar}} {\ tfrac {1} {2}} m \ omega {\ frac {(x_ {i} ^ {2} + x_ {f} ^ {2}) \ cos \ omega T-2x_ {i} x_ {f}} {\ sin \ omega T}} \ right )} \\ [6pt] & = \ sum _ {n = 0} ^ {\ infty} \ exp {\ left (- {\ frac {iE_ {n} T} {\ hbar}} \ right)} \ psi _ {n} (x_ {f}) \ psi _ {n} (x_ {i}) ^ {*} ~. \ end {alinhado}}}$

Usando as identidades i sin ωT =1/2e ^iωT (1 - e ^{−2 iωT} ) e cos ωT =1/2e ^iωT (1 + e ^{−2 iωT} ) , isso equivale a

${\ displaystyle K (x_ {f}, t_ {f}; x_ {i}, t_ {i}) = \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ right) ^ {\ frac {1} {2}} e ^ {\ frac {-i \ omega T} {2}} \ left (1-e ^ {- 2i \ omega T} \ right) ^ {- {\ frac {1} {2}}} \ exp {\ left (- {\ frac {m \ omega} {2 \ hbar}} \ left (\ left (x_ {i} ^ {2} + x_ {f} ^ {2} \ direita) {\ frac {1 + e ^ {- 2i \ omega T}} {1-e ^ {- 2i \ omega T}}} - {\ frac {4x_ {i} x_ {f} e ^ {- i \ omega T}} {1-e ^ {- 2i \ omega T}}} \ direita) \ direita)}.}$

Pode-se absorver todos os termos após o primeiro e ^{- iωT / 2} em R ( T ) , obtendo assim

${\ displaystyle K (x_ {f}, t_ {f}; x_ {i}, t_ {i}) = \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ right) ^ {\ frac {1} {2}} e ^ {\ frac {-i \ omega T} {2}} \ cdot R (T).}$

Pode-se finalmente expandir R ( T ) em potências de e ^{- iωT} : Todos os termos nesta expansão são multiplicados pelo fator e ^{- iωT / 2} na frente, produzindo os termos da forma

${\ displaystyle e ^ {\ frac {-i \ omega T} {2}} e ^ {- em \ omega T} = e ^ {- i \ omega T \ left ({\ frac {1} {2}} + n \ direita)} \ quad {\ text {para}} n = 0,1,2, \ ldots.}$

A comparação com a expansão de autoestado acima produz o espectro de energia padrão para o oscilador harmônico simples,

${\ displaystyle E_ {n} = \ left (n + {\ tfrac {1} {2}} \ right) \ hbar \ omega ~.}$

Potencial de Coulomb

A aproximação fatiada no tempo de Feynman não existe, no entanto, para as integrais de caminho da mecânica quântica mais importantes dos átomos, devido à singularidade do potencial de Coulomb e ²/rna origem. Somente após substituir o tempo t por outro parâmetro de pseudo-tempo dependente do caminho

${\ displaystyle s = \ int {\ frac {dt} {r (t)}}}$

a singularidade é removida e existe uma aproximação fatiada no tempo, que é exatamente integrável, uma vez que pode ser tornada harmônica por uma simples transformação de coordenadas, conforme descoberto em 1979 por İsmail Hakkı Duru e Hagen Kleinert . A combinação de uma transformação de tempo dependente de caminho e uma transformação de coordenada é uma ferramenta importante para resolver muitas integrais de caminho e é chamada genericamente de transformação Duru-Kleinert .

A equação de Schrödinger

A integral de caminho reproduz a equação de Schrödinger para o estado inicial e final, mesmo quando um potencial está presente. Isso é mais fácil de ver tomando uma integral de caminho em tempos infinitesimalmente separados.

${\ displaystyle \ psi (y; t + \ varepsilon) = \ int _ {- \ infty} ^ {\ infty} \ psi (x; t) \ int _ {x (t) = x} ^ {x (t + \ ( x) {\ bigr)} dt} Dx (t) \, dx \ qquad (1)}$

Como a separação de tempo é infinitesimal e as oscilações de cancelamento tornam-se severas para grandes valores de ẋ , a integral de caminho tem mais peso para y perto de x . Nesse caso, para a ordem mais baixa, a energia potencial é constante e apenas a contribuição da energia cinética não é trivial. (Esta separação dos termos de energia cinética e potencial no expoente é essencialmente a fórmula do produto Trotter .) O exponencial da ação é

${\ displaystyle e ^ {- i \ varepsilon V (x)} e ^ {i {\ frac {{\ dot {x}} ^ {2}} {2}} \ varepsilon}}$

O primeiro termo gira a fase de ψ ( x ) localmente por uma quantidade proporcional à energia potencial. O segundo termo é o propagador de partículas livres, correspondendo a i vezes um processo de difusão. Para a ordem mais baixa em ε, eles são aditivos; em qualquer caso, um tem com (1):

${\ displaystyle \ psi (y; t + \ varejpsilon) \ approx \ int \ psi (x; t) e ^ {- i \ varejpsilon V (x)} e ^ {\ frac {i (xy) ^ {2}} {2 \ varepsilon}} \, dx \ ,.}$

Como mencionado, a propagação em ψ é difusiva a partir da propagação de partículas livres, com uma rotação infinitesimal extra em fase que varia lentamente de ponto a ponto a partir do potencial:

${\ displaystyle {\ frac {\ partial \ psi} {\ partial t}} = i \ cdot \ left ({\ tfrac {1} {2}} \ nabla ^ {2} -V (x) \ right) \ psi \,}$

e esta é a equação de Schrödinger. A normalização da integral de caminho precisa ser corrigida exatamente da mesma maneira que no caso de partícula livre. Um potencial contínuo arbitrário não afeta a normalização, embora potenciais singulares exijam um tratamento cuidadoso.

Equações de movimento

Uma vez que os estados obedecem a equação de Schrödinger, a integral de trajetória devem reproduzir as equações de Heisenberg de movimento para as médias de x e X variáveis, mas é instrutivo ver isso diretamente. A abordagem direta mostra que os valores esperados calculados a partir da integral de caminho reproduzem os usuais da mecânica quântica.

Comece considerando a integral do caminho com algum estado inicial fixo

${\ displaystyle \ int \ psi _ {0} (x) \ int _ {x (0) = x} e ^ {iS (x, {\ dot {x}})} \, Dx \,}$

Agora, x ( t ) em cada momento separado é uma variável de integração separada. Portanto, é legítimo alterar as variáveis ​​na integral deslocando: x ( t ) = u ( t ) + ε ( t ) onde ε ( t ) é um deslocamento diferente a cada vez, mas ε (0) = ε ( T ) = 0 , uma vez que os terminais não estão integrados:

${\ displaystyle \ int \ psi _ {0} (x) \ int _ {u (0) = x} e ^ {iS (u + \ varejpsilon, {\ ponto {u}} + {\ ponto {\ varejpsilon}} )} \, Du \,}$

A mudança na integral da mudança é, para a primeira ordem infinitesimal em ε :

${\ displaystyle \ int \ psi _ {0} (x) \ int _ {u (0) = x} \ left (\ int {\ frac {\ partial S} {\ partial u}} \ varejpsilon + {\ frac {\ partial S} {\ partial {\ dot {u}}}} {\ dot {\ varepsilon}} \, dt \ right) e ^ {iS} \, Du \,}$

que, integrando por partes em t , dá:

${\ displaystyle \ int \ psi _ {0} (x) \ int _ {u (0) = x} - \ left (\ int \ left ({\ frac {d} {dt}} {\ frac {\ partial S} {\ parcial {\ ponto {u}}}} - {\ frac {\ parcial S} {\ parcial u}} \ direita) \ varepsilon (t) \, dt \ direita) e ^ {iS} \, Du \,}$

Mas isso foi apenas uma mudança de variáveis ​​de integração, o que não muda o valor da integral para qualquer escolha de ε ( t ) . A conclusão é que esta variação de primeira ordem é zero para um estado inicial arbitrário e em qualquer ponto arbitrário no tempo:

${\ displaystyle \ left \ langle \ psi _ {0} \ left | {\ frac {\ delta S} {\ delta x}} (t) \ right | \ psi _ {0} \ right \ rangle = 0}$

esta é a equação de movimento de Heisenberg.

Se a ação contém termos que multiplicam ẋ e x , no mesmo momento no tempo, as manipulações acima são apenas heurísticas, pois as regras de multiplicação para essas quantidades são tão não comutativas na integral de caminho quanto no formalismo do operador.

Aproximação de fase estacionária

Se a variação na ação excede ħ em muitas ordens de magnitude, normalmente temos interferência destrutiva diferente da vizinhança daquelas trajetórias que satisfazem a equação de Euler-Lagrange , que agora é reinterpretada como a condição para interferência construtiva. Isso pode ser demonstrado usando o método de fase estacionária aplicado ao propagador. À medida que ħ diminui, o exponencial na integral oscila rapidamente no domínio complexo para qualquer mudança na ação. Assim, no limite que ħ vai para zero, apenas pontos onde a ação clássica não varia contribuem para o propagador.

Relações de comutação canônica

A formulação da integral de caminho não deixa claro à primeira vista que as quantidades x e p não comutam. Na integral do caminho, essas são apenas variáveis ​​de integração e não têm uma ordem óbvia. Feynman descobriu que a não comutatividade ainda está presente.

Para ver isso, considere a integral de caminho mais simples, a caminhada browniana. Isso ainda não é mecânica quântica, então na integral de caminho a ação não é multiplicada por i :

${\ displaystyle S = \ int \ left ({\ frac {dx} {dt}} \ right) ^ {2} \, dt}$

A quantidade x ( t ) é flutuante e a derivada é definida como o limite de uma diferença discreta.

${\ displaystyle {\ frac {dx} {dt}} = {\ frac {x (t + \ varepsilon) -x (t)} {\ varejpsilon}}}$

A distância que um passeio aleatório percorre é proporcional a √ t , de modo que:

${\ displaystyle x (t + \ varepsilon) -x (t) \ approx {\ sqrt {\ varepsilon}}}$

Isso mostra que o passeio aleatório não é diferenciável, pois a razão que define a derivada diverge com a probabilidade um.

A quantidade xẋ é ambígua, com dois significados possíveis:

${\ displaystyle [1] = x {\ frac {dx} {dt}} = x (t) {\ frac {x (t + \ varepsilon) -x (t)} {\ varejpsilon}}}$

${\ displaystyle [2] = x {\ frac {dx} {dt}} = x (t + \ varejpsilon) {\ frac {x (t + \ varejpsilon) -x (t)} {\ varejpsilon}}}$

No cálculo elementar, os dois são diferentes apenas por um valor que vai para 0 quando ε vai para 0. Mas, neste caso, a diferença entre os dois não é 0:

${\ displaystyle [2] - [1] = {\ frac {{\ big (} x (t + \ varejpsilon) -x (t) {\ big)} ^ {2}} {\ varejpsilon}} \ aprox {\ frac {\ varepsilon} {\ varepsilon}}}$

Deixar

${\ displaystyle f (t) = {\ frac {{\ big (} x (t + \ varepsilon) -x (t) {\ big)} ^ {2}} {\ varepsilon}}}$

Então f ( t ) é uma quantidade estatística de flutuação rápida, cujo valor médio é 1, ou seja, um "processo gaussiano" normalizado. As flutuações de tal quantidade podem ser descritas por um Lagrangiano estatístico

${\ displaystyle {\ mathcal {L}} = (f (t) -1) ^ {2} \ ,,}$

e as equações de movimento para f derivadas da extremização da ação S correspondente a L apenas definem-na igual a 1. Em física, tal quantidade é "igual a 1 como uma identidade de operador". Em matemática, "converge fracamente para 1". Em ambos os casos, é 1 em qualquer valor esperado, ou quando a média é calculada em qualquer intervalo, ou para todos os fins práticos.

Definindo a ordem de tempo para ser a ordem do operador:

${\ displaystyle [x, {\ dot {x}}] = x {\ frac {dx} {dt}} - {\ frac {dx} {dt}} x = 1}$

Isso é chamado de lema Itō no cálculo estocástico e as relações de comutação canônicas (euclidianizadas) na física.

Para uma ação estatística geral, um argumento semelhante mostra que

${\ displaystyle \ left [x, {\ frac {\ partial S} {\ partial {\ dot {x}}}} \ right] = 1}$

e na mecânica quântica, a unidade imaginária extra na ação converte isso para a relação de comutação canônica,

${\ displaystyle [x, p] = i}$

Partícula em espaço curvo

Para uma partícula no espaço curvo, o termo cinético depende da posição, e o fatiamento de tempo acima não pode ser aplicado, sendo esta uma manifestação do notório problema de ordenação de operadores na mecânica quântica de Schrödinger. Pode-se, no entanto, resolver este problema transformando o caminho de espaço plano fatiado no tempo integral para espaço curvo usando uma transformação de coordenadas de vários valores ( mapeamento não holonômico explicado aqui ).

Fatores teóricos de medida

Às vezes (por exemplo, uma partícula se movendo em um espaço curvo), também temos fatores teóricos de medida na integral funcional:

${\ displaystyle \ int \ mu [x] e ^ {iS [x]} \, {\ mathcal {D}} x.}$

Este fator é necessário para restaurar a unidade.

Por exemplo, se

${\ displaystyle S = \ int \ left ({\ frac {m} {2}} g_ {ij} {\ dot {x}} ^ {i} {\ dot {x}} ^ {j} -V (x ) \ right) \, dt,}$

então significa que cada fatia espacial é multiplicada pela medida √ g . Essa medida não pode ser expressa como uma multiplicação funcional da medida D x porque eles pertencem a classes totalmente diferentes.

Valores de expectativa e elementos da matriz

Elementos de matriz do tipo assumem a forma ${\ displaystyle \ langle x_ {f} | e ^ {- {\ frac {i} {\ hbar}} {\ hat {H}} (t-t ')} F ({\ hat {x}}) e ^ {- {\ frac {i} {\ hbar}} {\ hat {H}} (t ')} | x_ {i} \ rangle}$

${\ displaystyle \ int _ {x (0) = x_ {i}} ^ {x (t) = x_ {f}} {\ mathcal {D}} [x] F (x (t ')) e ^ { {\ frac {i} {\ hbar}} \ int dtL (x (t), {\ dot {x}} (t))}}$.

Isso generaliza para vários operadores, por exemplo

${\ displaystyle \ langle x_ {f} | e ^ {- {\ frac {i} {\ hbar}} {\ hat {H}} (t-t_ {1})} F_ {1} ({\ hat { x}}) e ^ {- {\ frac {i} {\ hbar}} {\ hat {H}} (t_ {1} -t_ {2})} F_ {2} ({\ hat {x}} ) e ^ {- {\ frac {i} {\ hbar}} {\ hat {H}} (t_ {2})} | x_ {i} \ rangle = \ int _ {x (0) = x_ {i }} ^ {x (t) = x_ {f}} {\ mathcal {D}} [x] F_ {1} (x (t_ {1})) F_ {2} (x (t_ {2})) e ^ {{\ frac {i} {\ hbar}} \ int dtL (x (t), {\ dot {x}} (t))}}$,

e para o valor de expectativa geral

${\ displaystyle \ langle F \ rangle = {\ frac {\ int {\ mathcal {D}} [\ phi] F (\ phi) e ^ {{\ frac {i} {\ hbar}} S [\ phi] }} {\ int {\ mathcal {D}} [\ phi] e ^ {{\ frac {i} {\ hbar}} S [\ phi]}}}}$.

Integrais de caminho euclidiano

É muito comum em integrais de caminho realizar uma rotação Wick de tempos reais para imaginários. No cenário da teoria quântica de campos, a rotação de Wick muda a geometria do espaço-tempo de Lorentziana para Euclidiana; como resultado, as integrais de caminho com rotação de Wick são freqüentemente chamadas de integrais de caminho euclidianas.

Rotação de Wick e a fórmula de Feynman-Kac

Se substituirmos por , o operador de evolução no tempo será substituído por . (Esta mudança é conhecida como rotação Wick .) Se repetirmos a derivação da fórmula da integral do caminho nesta configuração, obteremos ${\ displaystyle t}$${\ displaystyle -it}$${\ displaystyle e ^ {- it {\ hat {H}} / \ hbar}}$${\ displaystyle e ^ {- t {\ hat {H}} / \ hbar}}$

${\ displaystyle \ psi (x, t) = {\ frac {1} {Z}} \ int _ {\ mathbf {x} (0) = x} e ^ {- S _ {\ mathrm {Euclidiano}} (\ mathbf {x}, {\ dot {\ mathbf {x}}}) / \ hbar} \ psi _ {0} (\ mathbf {x} (t)) \, {\ mathcal {D}} \ mathbf {x } \,}$,

onde está a ação euclidiana, dada por ${\ displaystyle S _ {\ mathrm {Euclidiano}}}$

${\ displaystyle S _ {\ mathrm {Euclidiano}} (\ mathbf {x}, {\ dot {\ mathbf {x}}}) = \ int \ left [{\ frac {m} {2}} | {\ dot {\ mathbf {x}}} (t) | ^ {2} + V (\ mathbf {x} (t)) \ right] \, dt}$.

Observe a mudança de sinal entre esta e a ação normal, onde o termo de energia potencial é negativo. (O termo euclidiano vem do contexto da teoria quântica de campos, onde a mudança do tempo real para o imaginário muda a geometria do espaço-tempo de Lorentziana para Euclidiana.)

Agora, a contribuição da energia cinética para a integral do caminho é a seguinte:

${\ displaystyle {\ frac {1} {Z}} \ int _ {\ mathbf {x} (0) = x} f (\ mathbf {x}) e ^ {- {\ frac {m} {2}} \ int | {\ dot {\ mathbf {x}}} | ^ {2} dt} \, {\ mathcal {D}} \ mathbf {x} \,}$

onde inclui toda a dependência remanescente do integrando no caminho. Esta integral tem uma interpretação matemática rigorosa como integração contra a medida de Wiener , denotada . A medida de Wiener, construída por Norbert Wiener, fornece uma base rigorosa para o modelo matemático de movimento browniano de Einstein . O subscrito indica que a medida é suportada em caminhos com . ${\ displaystyle f (\ mathbf {x})}$${\ displaystyle \ mu _ {x}}$${\ displaystyle x}$${\ displaystyle \ mu _ {x}}$${\ displaystyle \ mathbf {x}}$${\ displaystyle \ mathbf {x} (0) = x}$

Temos então uma versão rigorosa da integral de caminho de Feynman, conhecida como fórmula de Feynman-Kac :

${\ displaystyle \ psi (x, t) = \ int e ^ {- \ int V (\ mathbf {x} (t) \, dt / \ hbar} \, \ psi _ {0} (\ mathbf {x} (t)) \, d \ mu _ {x} (\ mathbf {x})}$,

onde agora satisfaz a versão girada de Wick da equação de Schrödinger, ${\ displaystyle \ psi (x, t)}$

${\ displaystyle \ hbar {\ frac {\ partial} {\ partial t}} \ psi (x, t) = - {\ hat {H}} \ psi (x, t)}$.

Embora a equação de Schrödinger com rotação de Wick não tenha um significado físico direto, propriedades interessantes do operador de Schrödinger podem ser extraídas estudando-o. ${\ displaystyle {\ hat {H}}}$

Muito do estudo das teorias quânticas de campo da perspectiva integral do caminho, tanto na literatura matemática quanto na física, é feito no cenário euclidiano, ou seja, após uma rotação de Wick. Em particular, existem vários resultados que mostram que se uma teoria de campo euclidiana com propriedades adequadas pode ser construída, pode-se então desfazer a rotação de Wick para recuperar a teoria física de Lorentz. Por outro lado, é muito mais difícil dar um significado às integrais de caminho (mesmo integrais de caminho euclidianas) na teoria quântica de campos do que na mecânica quântica.

A integral do caminho e a função de partição

A integral de caminho é apenas a generalização da integral acima para todos os problemas de mecânica quântica -

${\ displaystyle Z = \ int e ^ {\ frac {i {\ mathcal {S}} [\ mathbf {x}]} {\ hbar}} \, {\ mathcal {D}} \ mathbf {x} \ quad {\ text {onde}} {\ mathcal {S}} [\ mathbf {x}] = \ int _ {0} ^ {T} L [\ mathbf {x} (t), {\ ponto {\ mathbf { x}}} (t)] \, dt}$

é a ação do problema clássico em que se investiga o caminho começando no tempo t = 0 e terminando no tempo t = T , e denota integração sobre todos os caminhos. No limite clássico,, o caminho da ação mínima domina a integral, porque a fase de qualquer caminho fora deste flutua rapidamente e diferentes contribuições se cancelam. ${\ displaystyle {\ mathcal {D}} \ mathbf {x}}$${\ displaystyle {\ mathcal {S}} [\ mathbf {x}] \ gg \ hbar}$

A conexão com a mecânica estatística segue. Considerando apenas os caminhos que começam e terminam na mesma configuração, execute a rotação Wick it = τ , ou seja, torne o tempo imaginário, e integre todas as configurações possíveis de início-fim. A integral de caminho girada por Wick - descrita na subseção anterior, com a ação ordinária substituída por sua contraparte "euclidiana" - agora se assemelha à função de partição da mecânica estatística definida em um conjunto canônico com temperatura inversa proporcional ao tempo imaginário,1/T = k _B τ/ħ. Estritamente falando, porém, esta é a função de partição para uma teoria de campo estatística .

Claramente, essa analogia profunda entre a mecânica quântica e a mecânica estatística não pode depender da formulação. Na formulação canônica, vê-se que o operador unitário de evolução de um estado é dado por

${\ displaystyle | \ alpha; t \ rangle = e ^ {- {\ frac {iHt} {\ hbar}}} | \ alpha; 0 \ rangle}$

onde o estado α é evoluído a partir do tempo t = 0 . Se alguém faz uma rotação Wick aqui, e encontra a amplitude de ir de qualquer estado, de volta ao mesmo estado no tempo (imaginário) iT é dada por

${\ displaystyle Z = \ operatorname {Tr} \ left [e ^ {\ frac {-HT} {\ hbar}} \ right]}$

que é precisamente a função de partição da mecânica estatística para o mesmo sistema na temperatura citado anteriormente. Um aspecto dessa equivalência também era conhecido por Erwin Schrödinger, que observou que a equação nomeada em sua homenagem se parecia com a equação de difusão após a rotação de Wick. Observe, no entanto, que a integral do caminho euclidiano está na verdade na forma de um modelo clássico de mecânica estatística.

Teoria quântica de campos

Teoria quântica de campos
Diagrama de Feynman
História
Fundo Teoria de campo Eletromagnetismo Força fraca Força forte Mecânica quântica Relatividade especial Relatividade geral Teoria de calibre
Simetrias Simetria em mecânica quântica Simetria C Simetria P Simetria T Simetria de translação espacial Simetria de tradução de tempo Simetria de rotação Simetria de Lorentz Simetria de Poincaré Simetria de calibre Quebra de simetria explícita Quebra espontânea de simetria Teoria de Yang-Mills Carga Noether Carga topológica
Ferramentas Anomalia Cruzando Teoria de campo eficaz Valor de expectativa Fantasmas Faddeev-Popov Diagrama de Feynman Teoria de calibre reticulado Fórmula de redução LSZ Função de partição Propagator Quantização Regularização Renormalização Estado de vácuo Teorema de Wick Axiomas de Wightman
Equações Equação de Dirac Equação de Klein-Gordon Equações de Proca Equação de Wheeler-DeWitt Equações de Bargmann-Wigner
Modelo Padrão Eletrodinâmica quântica Interação eletrofraca Cromodinâmica quântica Mecanismo de Higgs
Teorias incompletas Teoria de campo quântico topológico Teoria das cordas Supersimetria Technicolor Teoria de tudo Gravidade quântica
Cientistas CD Anderson PW Anderson Bethe Bjorken Bogoliubov Brout Callan Coleman DeWitt Dirac Dyson Englert Fermi Feynman Fierz Fock Fröhlich Brilho Gell-Mann Bruto Guralnik Heisenberg Higgs Haag Hagen 't Hooft Jordânia Kendall Kibble Cordeiro Landau Lee Majorana Mills Nambu Nishijima Parisi Polyakov Salam Schwinger Skyrme Sudarshan Tomonaga Veltman ala Weinberg Weisskopf Weyl Wilczek Wilson Yang Yukawa
v t e

Ambas as abordagens de Schrödinger e Heisenberg da mecânica quântica destacam o tempo e não seguem o espírito da relatividade. Por exemplo, a abordagem de Heisenberg requer que os operadores de campo escalar obedeçam à relação de comutação

${\ displaystyle [\ varphi (x), \ partial _ {t} \ varphi (y)] = i \ delta ^ {3} (xy)}$

para duas posições espaciais simultâneas x e y , e isto não é um conceito relativisticamente invariante. Os resultados de um cálculo são covariantes, mas a simetria não é aparente nos estágios intermediários. Se os cálculos ingênuos da teoria de campo não produzissem respostas infinitas no limite do contínuo, isso não teria sido um grande problema - teria sido apenas uma má escolha de coordenadas. Mas a falta de simetria significa que as quantidades infinitas devem ser eliminadas, e as coordenadas ruins tornam quase impossível eliminar a teoria sem prejudicar a simetria. Isso torna difícil extrair as previsões físicas, que requerem um procedimento de limitação cuidadoso .

O problema da simetria perdida também aparece na mecânica clássica, onde a formulação hamiltoniana também destaca o tempo superficialmente. A formulação Lagrangiana torna a invariância relativística aparente. Da mesma forma, a integral de caminho é manifestamente relativística. Ele reproduz a equação de Schrödinger, as equações de movimento de Heisenberg e as relações de comutação canônicas e mostra que elas são compatíveis com a relatividade. Ele estende a álgebra de operador do tipo de Heisenberg para regras de produto de operador , que são novas relações difíceis de ver no antigo formalismo.

Além disso, diferentes escolhas de variáveis ​​canônicas levam a formulações aparentemente muito diferentes da mesma teoria. As transformações entre as variáveis ​​podem ser muito complicadas, mas a integral do caminho as transforma em mudanças razoavelmente diretas das variáveis ​​de integração. Por essas razões, a integral de caminho de Feynman tornou os formalismos anteriores amplamente obsoletos.

O preço de uma representação integral de caminho é que a unitariedade de uma teoria não é mais evidente, mas pode ser provada alterando variáveis ​​para alguma representação canônica. A própria integral de caminho também lida com espaços matemáticos maiores do que o normal, o que requer matemática mais cuidadosa, que nem todos foram totalmente resolvidos. O caminho integral historicamente não foi aceito imediatamente, em parte porque demorou muitos anos para incorporar férmions adequadamente. Isso exigia que os físicos inventassem um objeto matemático inteiramente novo - a variável de Grassmann - que também permitia que mudanças de variáveis ​​fossem feitas naturalmente, além de permitir a quantização restrita .

As variáveis ​​de integração na integral do caminho são sutilmente não comutáveis. O valor do produto de dois operadores de campo no que parece o mesmo ponto depende de como os dois pontos são ordenados no espaço e no tempo. Isso faz com que algumas identidades ingênuas falhem .

O propagador

Nas teorias relativísticas, existe uma representação de partícula e de campo para cada teoria. A representação do campo é uma soma de todas as configurações do campo e a representação da partícula é uma soma de diferentes caminhos das partículas.

A formulação não relativística é tradicionalmente dada em termos de caminhos de partículas, não de campos. Lá, a integral de caminho nas variáveis ​​usuais, com condições de contorno fixas, dá a amplitude de probabilidade de uma partícula ir do ponto x ao ponto y no tempo T :

${\ displaystyle K (x, y; T) = \ langle y; T \ mid x; 0 \ rangle = \ int _ {x (0) = x} ^ {x (T) = y} e ^ {iS [ x]} \, Dx.}$

Isso é chamado de propagador . Sobrepor diferentes valores da posição inicial x com um estado inicial arbitrário ψ ₀ ( x ) constrói o estado final:

${\ displaystyle \ psi _ {T} (y) = \ int _ {x} \ psi _ {0} (x) K (x, y; T) \, dx = \ int ^ {x (T) = y } \ psi _ {0} (x (0)) e ^ {iS [x]} \, Dx.}$

Para um sistema espacialmente homogêneo, onde K ( x , y ) é apenas uma função de ( x - y ) , a integral é uma convolução , o estado final é o estado inicial convolvido com o propagador:

${\ displaystyle \ psi _ {T} = \ psi _ {0} * K (; T).}$

Para uma partícula livre de massa m , o propagador pode ser avaliado explicitamente a partir da integral do caminho ou observando que a equação de Schrödinger é uma equação de difusão no tempo imaginário e a solução deve ser uma gaussiana normalizada:

${\ displaystyle K (x, y; T) \ propto e ^ {\ frac {im (xy) ^ {2}} {2T}}.}$

Tomar a transformada de Fourier em ( x - y ) produz outro Gaussiano:

${\ displaystyle K (p; T) = e ^ {\ frac {iTp ^ {2}} {2m}},}$

e no espaço- p o fator de proporcionalidade aqui é constante no tempo, como será verificado a seguir. A transformada de Fourier no tempo, estendendo K ( p ; T ) a zero para tempos negativos, dá a função de Green, ou o propagador do espaço de frequência:

${\ displaystyle G _ {\ text {F}} (p, E) = {\ frac {-i} {E - {\ frac {{\ vec {p}} ^ {2}} {2m}} + i \ varejpsilon}},}$

que é o recíproco do operador que aniquila a função de onda na equação de Schrödinger, que não teria dado certo se o fator de proporcionalidade não fosse constante na representação do p- espaço.

O termo infinitesimal no denominador é um pequeno número positivo, o que garante que a transformada inversa de Fourier em E será diferente de zero apenas para tempos futuros. No passado, o contorno inverso da transformada de Fourier fecha em direção aos valores de E onde não há singularidade. Isto garante que K propaga a partícula para o futuro e é a razão para o subscrito "F" na L . O termo infinitesimal pode ser interpretado como uma rotação infinitesimal em direção ao tempo imaginário.

Também é possível reexpressar a evolução não relativística do tempo em termos de propagadores indo em direção ao passado, uma vez que a equação de Schrödinger é reversível no tempo. O propagador do passado é o mesmo que o propagador do futuro, exceto pela diferença óbvia de que ele desaparece no futuro e, no Gaussiano, t é substituído por - t . Nesse caso, a interpretação é que essas são as quantidades para convolver a função de onda final de forma a obter a função de onda inicial:

${\ displaystyle G _ {\ text {B}} (p, E) = {\ frac {-i} {- E - {\ frac {i {\ vec {p}} ^ {2}} {2m}} + i \ varepsilon}}.}$

Dado que a única mudança quase idêntica é o sinal de E e ε , o parâmetro E na função de Green pode ser a energia se os caminhos estão indo em direção ao futuro, ou o negativo da energia se os caminhos estão indo em direção ao passado.

Para uma teoria não relativística, o tempo medido ao longo do caminho de uma partícula em movimento e o tempo medido por um observador externo são os mesmos. Na relatividade, isso não é mais verdade. Para uma teoria relativística, o propagador deve ser definido como a soma de todos os caminhos que viajam entre dois pontos em um tempo fixo próprio, conforme medido ao longo do caminho (esses caminhos descrevem a trajetória de uma partícula no espaço e no tempo):

${\ displaystyle K (xy, \ mathrm {T}) = \ int _ {x (0) = x} ^ {x (\ mathrm {T}) = y} e ^ {i \ int _ {0} ^ { \ mathrm {T}} {\ sqrt {{\ dot {x}} ^ {2}}} - \ alpha \, d \ tau}.}$

A integral acima não é trivial de interpretar por causa da raiz quadrada. Felizmente, existe um truque heurístico. A soma é sobre o comprimento do arco relativístico do caminho de uma quantidade oscilante e, como a integral não relativística do caminho, deve ser interpretada como ligeiramente girada no tempo imaginário. A função K ( x - y , τ ) pode ser avaliada quando a soma é sobre caminhos no espaço euclidiano:

${\ displaystyle K (xy, \ mathrm {T}) = e ^ {- \ alpha \ mathrm {T}} \ int _ {x (0) = x} ^ {x (\ mathrm {T}) = y} e ^ {- L}.}$

Isso descreve a soma de todos os caminhos de comprimento Τ do exponencial de menos o comprimento. Isso pode receber uma interpretação de probabilidade. A soma de todos os caminhos é uma média de probabilidade de um caminho construído passo a passo. O número total de etapas é proporcional a Τ , e cada etapa é menos provável quanto mais longa for. Pelo teorema do limite central , o resultado de muitas etapas independentes é um Gaussiano de variância proporcional a Τ :

${\ displaystyle K (xy, \ mathrm {T}) = e ^ {- \ alpha \ mathrm {T}} e ^ {- {\ frac {(xy) ^ {2}} {\ mathrm {T}}} }.}$

A definição usual do propagador relativístico pede apenas que a amplitude seja para viajar de x a y , após somar todos os tempos adequados possíveis que poderia levar:

${\ displaystyle K (xy) = \ int _ {0} ^ {\ infty} K (xy, \ mathrm {T}) W (\ mathrm {T}) \, d \ mathrm {T},}$

onde W (Τ) é um fator de peso, a importância relativa de caminhos de diferentes tempos próprios. Pela simetria de translação em tempo próprio, este peso só pode ser um fator exponencial e pode ser absorvido pela constante α :

${\ displaystyle K (xy) = \ int _ {0} ^ {\ infty} e ^ {- {\ frac {(xy) ^ {2}} {\ mathrm {T}}} - \ alpha \ mathrm {T }} \, d \ mathrm {T}.}$

Esta é a representação de Schwinger . Tomar uma transformada de Fourier sobre a variável ( x - y ) pode ser feito para cada valor de Τ separadamente, e como cada contribuição separada de Τ é uma Gaussiana, dá cuja transformada de Fourier é outra Gaussiana com largura recíproca. Portanto, no espaço- p , o propagador pode ser reexpresso simplesmente:

${\ displaystyle K (p) = \ int _ {0} ^ {\ infty} e ^ {- \ mathrm {T} p ^ {2} - \ mathrm {T} \ alpha} \, d \ mathrm {T} = {\ frac {1} {p ^ {2} + \ alpha}},}$

que é o propagador euclidiano de uma partícula escalar. Girar p ₀ para ser imaginário dá o propagador relativístico usual, até um fator de - ie uma ambigüidade, que será esclarecida a seguir:

${\ displaystyle K (p) = {\ frac {i} {p_ {0} ^ {2} - {\ vec {p}} ^ {2} -m ^ {2}}}.}$

Esta expressão pode ser interpretada no limite não relativístico, onde é conveniente dividi-la em frações parciais :

${\ displaystyle 2p_ {0} K (p) = {\ frac {i} {p_ {0} - {\ sqrt {{\ vec {p}} ^ {2} + m ^ {2}}}}} + {\ frac {i} {p_ {0} + {\ sqrt {{\ vec {p}} ^ {2} + m ^ {2}}}}}.}$

Para estados onde uma partícula não relativística está presente, a função de onda inicial tem uma distribuição de frequência concentrada perto de p ₀ = m . Ao convolver com o propagador, que no espaço p significa apenas multiplicar pelo propagador, o segundo termo é suprimido e o primeiro termo é realçado. Para frequências próximas a p ₀ = m , o primeiro termo dominante tem a forma

${\ displaystyle 2mK _ {\ text {NR}} (p) = {\ frac {i} {(p_ {0} -m) - {\ frac {{\ vec {p}} ^ {2}} {2m} }}}.}$

Esta é a expressão para a função de Green não relativística de uma partícula de Schrödinger livre.

O segundo termo também tem um limite não relativístico, mas esse limite se concentra nas frequências que são negativas. O segundo pólo é dominado por contribuições de caminhos onde o tempo adequado e o tempo coordenado estão marcando em sentido oposto, o que significa que o segundo termo deve ser interpretado como a antipartícula. A análise não relativística mostra que com esta forma a antipartícula ainda possui energia positiva.

A maneira apropriada de expressar isso matematicamente é que, adicionando um pequeno fator de supressão no tempo adequado, o limite onde t → −∞ do primeiro termo deve desaparecer, enquanto o limite t → + ∞ do segundo termo deve desaparecer. Na transformada de Fourier, isso significa deslocar ligeiramente o pólo em p ₀ , de modo que a transformada de Fourier inversa pegue um pequeno fator de decaimento em uma das direções de tempo:

${\ displaystyle K (p) = {\ frac {i} {p_ {0} - {\ sqrt {{\ vec {p}} ^ {2} + m ^ {2}}} + i \ varepsilon}} + {\ frac {i} {p_ {0} - {\ sqrt {{\ vec {p}} ^ {2} + m ^ {2}}} - i \ varepsilon}}.}$

Sem esses termos, a contribuição do pólo não poderia ser avaliada de forma inequívoca ao tomar a transformada de Fourier inversa de p ₀ . Os termos podem ser recombinados:

${\ displaystyle K (p) = {\ frac {i} {p ^ {2} -m ^ {2} + i \ varepsilon}},}$

que, quando fatorado, produz termos infinitesimais de sinais opostos em cada fator. Esta é a forma matematicamente precisa do propagador de partículas relativísticas, livre de quaisquer ambigüidades. O termo ε introduz uma pequena parte imaginária para α = m ² , que na versão de Minkowski é uma pequena supressão exponencial de caminhos longos.

Portanto, no caso relativístico, a representação integral do caminho de Feynman do propagador inclui caminhos que retrocedem no tempo, que descrevem antipartículas. Os caminhos que contribuem para o propagador relativístico avançam e retrocedem no tempo, e a interpretação disso é que a amplitude para uma partícula livre viajar entre dois pontos inclui amplitudes para a partícula flutuar em uma antipartícula, viajar de volta no tempo, então para a frente novamente.

Ao contrário do caso não relativístico, é impossível produzir uma teoria relativística da propagação local de partículas sem incluir antipartículas. Todos os operadores diferenciais locais têm inversos diferentes de zero fora do cone de luz, o que significa que é impossível evitar que uma partícula viaje mais rápido que a luz. Tal partícula não pode ter uma função de Green que só seja diferente de zero no futuro em uma teoria relativisticamente invariante.

Funcionais de campos

No entanto, a formulação da integral de caminho também é extremamente importante na aplicação direta à teoria quântica de campos, na qual os "caminhos" ou histórias sendo considerados não são os movimentos de uma única partícula, mas as possíveis evoluções no tempo de um campo sobre todo o espaço. A ação é referida tecnicamente como um funcional do campo: S [ ϕ ] , onde o campo ϕ ( x ^μ ) é ele próprio uma função do espaço e do tempo, e os colchetes são um lembrete de que a ação depende de todos os campos valores em todos os lugares, não apenas algum valor particular. Uma dessas funções dadas ϕ ( x ^μ ) do espaço - tempo é chamada de configuração de campo . Em princípio, integra-se a amplitude de Feynman sobre a classe de todas as configurações de campo possíveis.

Muito do estudo formal de QFT é dedicado às propriedades da integral funcional resultante, e muitos esforços (ainda não totalmente bem-sucedidos) foram feitos para tornar essas integrais funcionais matematicamente precisas.

Essa integral funcional é extremamente semelhante à função de partição na mecânica estatística . Com efeito, é por vezes chamado um função de partição , e os dois são essencialmente matematicamente idêntica com excepção do factor de i no expoente em postulado de Feynman 3. Analiticamente continuando o integrante de uma variável de tempo imaginário (chamado de rotação Wick ) faz com que o integrante funcional ainda mais como uma função de partição estatística e também doma algumas das dificuldades matemáticas de trabalhar com essas integrais.

Valores de expectativa

Em teoria quântica de campo , se a acção é dado pela funcional S de configurações de campo (o qual só depende localmente nos campos), em seguida, o ordenou-tempo valor expectativa vácuo de polinomialmente delimitada funcional F , ⟨ F ⟩ , é dada pela

${\ displaystyle \ langle F \ rangle = {\ frac {\ int {\ mathcal {D}} \ varphi F [\ varphi] e ^ {i {\ mathcal {S}} [\ varphi]}} {\ int { \ mathcal {D}} \ varphi e ^ {i {\ mathcal {S}} [\ varphi]}}}.}$

O símbolo ∫ D ϕ aqui é uma maneira concisa de representar a integral de dimensão infinita sobre todas as configurações de campo possíveis em todo o espaço-tempo. Como afirmado acima, a integral de caminho sem adornos no denominador garante a normalização adequada.

Como uma probabilidade

Estritamente falando, a única pergunta que pode ser feita em física é: que fração de estados que satisfazem a condição A também satisfazem a condição B ? A resposta para isso é um número entre 0 e 1, que pode ser interpretado como uma probabilidade condicional , escrita como P ( B | A ) . Em termos de integração de caminhos, uma vez que P ( B | A ) =P ( A ∩ B ) / P ( A ), isso significa

${\ displaystyle \ operatorname {P} (B \ mid A) = {\ frac {\ sum _ {F \ subconjunto A \ cap B} \ left | \ int {\ mathcal {D}} \ varphi O _ {\ text { in}} [\ varphi] e ^ {i {\ mathcal {S}} [\ varphi]} F [\ varphi] \ right | ^ {2}} {\ sum _ {F \ subconjunto A} \ left | \ int {\ mathcal {D}} \ varphi O _ {\ text {in}} [\ varphi] e ^ {i {\ mathcal {S}} [\ varphi]} F [\ varphi] \ right | ^ {2} }},}$

onde o funcional O _em [ ϕ ] é a superposição de todos os estados de entrada que poderiam levar aos estados nos quais estamos interessados. Em particular, este poderia ser um estado correspondente ao estado do Universo logo após o Big Bang , embora para cálculo isso pode ser simplificado usando métodos heurísticos. Como essa expressão é um quociente de integrais de caminho, ela é normalizada naturalmente.

Equações de Schwinger-Dyson

Visto que esta formulação da mecânica quântica é análoga ao princípio de ação clássico, pode-se esperar que as identidades relativas à ação na mecânica clássica tenham contrapartes quânticas deriváveis ​​de uma integral funcional. Frequentemente este é o caso.

Na linguagem da análise funcional, podemos escrever as equações de Euler-Lagrange como

${\ displaystyle {\ frac {\ delta {\ mathcal {S}} [\ varphi]} {\ delta \ varphi}} = 0}$

(o lado esquerdo é uma derivada funcional ; a equação significa que a ação é estacionária sob pequenas mudanças na configuração do campo). Os análogos quânticos dessas equações são chamados de equações de Schwinger-Dyson .

Se a medida funcional D ϕ acabar sendo invariante translacionalmente (assumiremos isso para o resto deste artigo, embora isso não seja válido para, digamos, modelos sigma não lineares ), e se assumirmos que após uma rotação de Wick

${\ displaystyle e ^ {i {\ mathcal {S}} [\ varphi]},}$

que agora se torna

${\ displaystyle e ^ {- H [\ varphi]}}$

para algum H , ele vai para zero mais rápido do que um recíproco de qualquer polinômio para grandes valores de φ , então podemos integrar por partes (após uma rotação de Wick, seguida por uma rotação de Wick de volta) para obter as seguintes equações de Schwinger-Dyson para o expectativa:

${\ displaystyle \ left \ langle {\ frac {\ delta F [\ varphi]} {\ delta \ varphi}} \ right \ rangle = -i \ left \ langle F [\ varphi] {\ frac {\ delta {\ mathcal {S}} [\ varphi]} {\ delta \ varphi}} \ right \ rangle}$

para qualquer F funcional polinomialmente limitado . Na notação deWitt, isso parece

${\ displaystyle \ left \ langle F _ {, i} \ right \ rangle = -i \ left \ langle F {\ mathcal {S}} _ {, i} \ right \ rangle.}$

Essas equações são análogas às equações EL no shell . A ordem de tempo é obtida antes das derivadas de tempo dentro de S _{, i} .

Se J (chamado de campo de origem ) é um elemento do espaço dual das configurações de campo (que tem pelo menos uma estrutura afim por causa da suposição da invariância translacional para a medida funcional), então o Z funcional gerador dos campos de origem está definido para ser

${\ displaystyle Z [J] = \ int {\ mathcal {D}} \ varphi e ^ {i \ left ({\ mathcal {S}} [\ varphi] + \ langle J, \ varphi \ rangle \ right)} .}$

Observe que

${\ displaystyle {\ frac {\ delta ^ {n} Z} {\ delta J (x_ {1}) \ cdots \ delta J (x_ {n})}} [J] = i ^ {n} \, Z [J] \, \ left \ langle \ varphi (x_ {1}) \ cdots \ varphi (x_ {n}) \ right \ rangle _ {J},}$

ou

${\ displaystyle Z ^ {, i_ {1} \ cdots i_ {n}} [J] = i ^ {n} Z [J] \ left \ langle \ varphi ^ {i_ {1}} \ cdots \ varphi ^ { i_ {n}} \ right \ rangle _ {J},}$

Onde

${\ displaystyle \ langle F \ rangle _ {J} = {\ frac {\ int {\ mathcal {D}} \ varphi F [\ varphi] e ^ {i \ left ({\ mathcal {S}} [\ varphi ] + \ langle J, \ varphi \ rangle \ right)}} {\ int {\ mathcal {D}} \ varphi e ^ {i \ left ({\ mathcal {S}} [\ varphi] + \ langle J, \ varphi \ rangle \ right)}}}.}$

Basicamente, se D φ e ^{i S [ φ ]} é visto como uma distribuição funcional (isso não deve ser tomado muito literalmente como uma interpretação de QFT , ao contrário de seu análogo de mecânica estatística girada por Wick , porque temos complicações de ordenação de tempo aqui!) , em seguida, ⟨ φ ( x ₁ ) ... φ ( x _n )⟩ são os seus momentos , e Z é a sua transformada de Fourier .

Se F é um funcional de φ , então para um operador K , F [ K ] é definido como o operador que substitui K por φ . Por exemplo, se

${\ displaystyle F [\ varphi] = {\ frac {\ partial ^ {k_ {1}}} {\ partial x_ {1} ^ {k_ {1}}}} \ varphi (x_ {1}) \ cdots { \ frac {\ parcial ^ {k_ {n}}} {\ parcial x_ {n} ^ {k_ {n}}}} \ varphi (x_ {n}),}$

e G é um funcional de J , então

${\ displaystyle F \ left [-i {\ frac {\ delta} {\ delta J}} \ right] G [J] = (- i) ^ {n} {\ frac {\ partial ^ {k_ {1} }} {\ parcial x_ {1} ^ {k_ {1}}}} {\ frac {\ delta} {\ delta J (x_ {1})}} \ cdots {\ frac {\ parcial ^ {k_ {n }}} {\ parcial x_ {n} ^ {k_ {n}}}} {\ frac {\ delta} {\ delta J (x_ {n})}} G [J].}$

Então, a partir das propriedades dos integrais funcionais

${\ displaystyle \ left \ langle {\ frac {\ delta {\ mathcal {S}}} {\ delta \ varphi (x)}} [\ varphi] + J (x) \ right \ rangle _ {J} = 0 }$

obtemos a equação "mestre" de Schwinger-Dyson:

${\ displaystyle {\ frac {\ delta {\ mathcal {S}}} {\ delta \ varphi (x)}} \ left [-i {\ frac {\ delta} {\ delta J}} \ right] Z [ J] + J (x) Z [J] = 0,}$

ou

${\ displaystyle {\ mathcal {S}} _ {, i} [- i \ parcial] Z + J_ {i} Z = 0.}$

Se a medida funcional não for invariante translacionalmente, pode ser possível expressá-la como o produto M [ φ ] D φ , onde M é uma medida funcional e D φ é uma medida invariante translacionalmente. Isso é verdade, por exemplo, para modelos sigma não lineares em que o espaço-alvo é difeomórfico para R ⁿ . No entanto, se a variedade de destino for algum espaço topologicamente não trivial, o conceito de uma tradução nem mesmo faz qualquer sentido.

Nesse caso, teríamos que substituir o S nesta equação por outro funcional

${\ displaystyle {\ hat {\ mathcal {S}}} = {\ mathcal {S}} - i \ ln M.}$

Se expandirmos essa equação como uma série de Taylor sobre J = 0, obteremos todo o conjunto de equações de Schwinger-Dyson.

Localização

As integrais de caminho são geralmente consideradas como a soma de todos os caminhos através de um espaço-tempo infinito. No entanto, na teoria quântica de campos local , restringiríamos tudo para ficar dentro de uma região causalmente completa finita , por exemplo, dentro de um cone de luz duplo. Isso dá uma definição mais matematicamente precisa e fisicamente rigorosa da teoria quântica de campos.

Identidades de Ward – Takahashi

Agora, que tal o teorema de Noether do on shell para o caso clássico? Ele também tem um análogo quântico? Sim, mas com uma ressalva. A medida funcional teria que ser invariável sob o grupo de um parâmetro de transformação de simetria também.

Vamos apenas assumir para simplificar aqui que a simetria em questão é local (não local no sentido de uma simetria de calibre , mas no sentido de que o valor transformado do campo em qualquer ponto dado sob uma transformação infinitesimal dependeria apenas da configuração do campo sobre uma vizinhança arbitrariamente pequena do ponto em questão). Vamos também supor que a ação é local no sentido de que é a integral no espaço-tempo de um Lagrangiano , e que

${\ displaystyle Q [{\ mathcal {L}} (x)] = \ partial _ {\ mu} f ^ {\ mu} (x)}$

para alguma função f onde f depende apenas localmente de φ (e possivelmente da posição do espaço-tempo).

Se não assumirmos nenhuma condição de contorno especial, isso não seria uma simetria "verdadeira" no verdadeiro sentido do termo em geral, a menos que f = 0 ou algo assim. Aqui, Q é uma derivação que gera o único grupo de parâmetros em questão. Poderíamos ter antiderivações também, como BRST e supersimetria .

Vamos supor também

${\ displaystyle \ int {\ mathcal {D}} \ varphi \, Q [F] [\ varphi] = 0}$

para qualquer F funcional polinomialmente limitado . Essa propriedade é chamada de invariância da medida. E isso não acontece em geral. Veja anomalia (física) para mais detalhes.

Então,

${\ displaystyle \ int {\ mathcal {D}} \ varphi \, Q \ left [Fe ^ {iS} \ right] [\ varphi] = 0,}$

que implica

${\ displaystyle \ langle Q [F] \ rangle + i \ left \ langle F \ int _ {\ partial V} f ^ {\ mu} \, ds _ {\ mu} \ right \ rangle = 0}$

onde a integral está além do limite. Este é o análogo quântico do teorema de Noether.

Agora, vamos assumir ainda mais que Q é uma integral local

${\ displaystyle Q = \ int d ^ {d} x \, q (x)}$

Onde

${\ displaystyle q (x) [\ varphi (y)] = \ delta ^ {(d)} (Xy) Q [\ varphi (y)] \,}$

de modo a

${\ displaystyle q (x) [S] = \ partial _ {\ mu} j ^ {\ mu} (x) \,}$

Onde

${\ displaystyle j ^ {\ mu} (x) = f ^ {\ mu} (x) - {\ frac {\ partial} {\ partial (\ partial _ {\ mu} \ varphi)}} {\ mathcal { L}} (x) Q [\ varphi] \,}$

(isso pressupõe que o Lagrangiano dependa apenas de φ e de suas primeiras derivadas parciais! Lagrangianos mais gerais exigiriam uma modificação nesta definição!). Não estamos insistindo que q ( x ) é o gerador de uma simetria (ou seja, não estamos insistindo no princípio de calibre ), mas apenas que Q é. E também assumimos a suposição ainda mais forte de que a medida funcional é invariante localmente:

${\ displaystyle \ int {\ mathcal {D}} \ varphi \, q (x) [F] [\ varphi] = 0.}$

Então, teríamos

${\ displaystyle \ langle q (x) [F] \ rangle + i \ langle Fq (x) [S] \ rangle = \ langle q (x) [F] \ rangle + i \ left \ langle F \ partial _ { \ mu} j ^ {\ mu} (x) \ right \ rangle = 0.}$

Alternativamente,

${\ displaystyle q (x) [S] \ left [-i {\ frac {\ delta} {\ delta J}} \ right] Z [J] + J (x) Q [\ varphi (x)] \ left [-i {\ frac {\ delta} {\ delta J}} \ right] Z [J] = \ partial _ {\ mu} j ^ {\ mu} (x) \ left [-i {\ frac {\ delta} {\ delta J}} \ direita] Z [J] + J (x) Q [\ varphi (x)] \ esquerda [-i {\ frac {\ delta} {\ delta J}} \ direita] Z [J] = 0.}$

As duas equações acima são as identidades Ward – Takahashi .

Agora, para o caso em que f = 0 , podemos esquecer todas as condições de contorno e suposições de localidade. Nós simplesmente teríamos

${\ displaystyle \ left \ langle Q [F] \ right \ rangle = 0.}$

Alternativamente,

${\ displaystyle \ int d ^ {d} x \, J (x) Q [\ varphi (x)] \ left [-i {\ frac {\ delta} {\ delta J}} \ right] Z [J] = 0.}$

Ressalvas

A necessidade de reguladores e renormalização

As integrais de caminho, conforme definidas aqui, requerem a introdução de reguladores . Mudar a escala do regulador leva ao grupo de renormalização . Na verdade, a renormalização é o principal obstáculo para tornar as integrais de caminho bem definidas.

Solicitando receita

Independentemente de se trabalhar no espaço de configuração ou no espaço de fase, ao equacionar o formalismo do operador e a formulação integral do caminho, uma prescrição de ordenação é necessária para resolver a ambigüidade na correspondência entre os operadores não comutativos e as funções comutativas que aparecem nos integrantes do caminho. Por exemplo, o operador pode ser traduzido para trás como qualquer , ou dependendo de se se escolhe o , , ou Weyl ordenação prescrição; inversamente, pode ser traduzido para tanto , ou para o mesmo respectiva escolha de prescrição ordenação. ${\ displaystyle {\ frac {1} {2}} ({\ hat {q}} {\ hat {p}} + {\ hat {p}} {\ hat {q}})}$${\ displaystyle qp - {\ frac {i \ hbar} {2}}}$${\ displaystyle qp + {\ frac {i \ hbar} {2}}}$${\ displaystyle qp}$${\ displaystyle {\ hat {q}} {\ hat {p}}}$${\ displaystyle {\ hat {p}} {\ hat {q}}}$${\ displaystyle qp}$${\ displaystyle {\ hat {q}} {\ hat {p}}}$${\ displaystyle {\ hat {p}} {\ hat {q}}}$${\ displaystyle {\ frac {1} {2}} ({\ hat {q}} {\ hat {p}} + {\ hat {p}} {\ hat {q}})}$

O caminho integral na interpretação da mecânica quântica

Em uma interpretação da mecânica quântica , a interpretação da "soma das histórias", a integral do caminho é considerada fundamental e a realidade é vista como uma única "classe" indistinguível de caminhos que compartilham os mesmos eventos. Para essa interpretação, é fundamental entender o que exatamente é um evento. O método da soma das histórias dá resultados idênticos à mecânica quântica canônica, e Sinha e Sorkin afirmam que a interpretação explica o paradoxo de Einstein-Podolsky-Rosen sem recorrer à não localidade .

Alguns defensores das interpretações da mecânica quântica que enfatizam a decoerência tentaram tornar mais rigorosa a noção de extrair uma história clássica de "granulação grossa" do espaço de todas as histórias possíveis.

Gravidade quântica

Enquanto na mecânica quântica a formulação da integral de caminho é totalmente equivalente a outras formulações, pode ser que ela possa ser estendida para a gravidade quântica, o que a tornaria diferente do modelo espacial de Hilbert . Feynman teve algum sucesso nessa direção, e seu trabalho foi estendido por Hawking e outros. As abordagens que usam este método incluem triangulações dinâmicas causais e modelos de spinfoam .

Tunelamento quântico

O tunelamento quântico pode ser modelado usando a formação integral do caminho para determinar a ação da trajetória através de uma barreira potencial. Usando a aproximação WKB , a taxa de tunelamento ( Γ ) pode ser determinada para ser da forma

${\ displaystyle \ Gamma = A _ {\ mathrm {o}} \ exp \ left (- {\ frac {S _ {\ mathrm {eff}}} {\ hbar}} \ right)}$

com a ação efetiva S _eff e fator pré-exponencial A _o . Esta forma é especificamente útil em um sistema dissipativo , no qual os sistemas e arredores devem ser modelados juntos. Usando a equação de Langevin para modelar o movimento browniano , a formação integral do caminho pode ser usada para determinar uma ação efetiva e um modelo pré-exponencial para ver o efeito da dissipação no tunelamento. A partir deste modelo, as taxas de tunelamento de sistemas macroscópicos (em temperaturas finitas) podem ser previstas.

Veja também

• Justificativa teórica e experimental para a equação de Schrödinger
• Forças estáticas e troca de partículas virtuais
• Tabuleiro de damas Feynman
• Integral de Berezin
• Propagadores
• Teoria do absorvedor de Wheeler-Feynman
• Fórmula de Feynman-Kac
• Integrais de caminho na ciência de polímeros

Observações

Notas

Referências

• Ahmad, Ishfaq (1971). Integrais matemáticos na natureza quântica . O núcleo. pp. 189–209.
• Albeverio, S .; Hoegh-Krohn., R. & Mazzucchi, S (2008). Teoria Matemática da Integral do Caminho de Feynman . Notas de aula em matemática 523. Springer-Verlag. ISBN 9783540769569.
• Caldeira, AO ; Leggett, AJ (1983). "Tunelamento quântico em um sistema dissipativo". Annals of Physics . 149 (2): 374–456. Bibcode : 1983AnPhy.149..374C . doi : 10.1016 / 0003-4916 (83) 90202-6 .
• Cartier, P ; DeWitt-Morette, Cécile (1995). “Uma nova perspectiva de integração funcional”. Journal of Mathematical Physics . 36 (5): 2137–2340. arXiv : funct-an / 9602005 . Bibcode : 1995JMP .... 36.2237C . doi : 10.1063 / 1.531039 . S2CID  119581543 .
• Chaichian, M .; Demichev, AP (2001). "Introdução" . Path Integrals in Physics Volume 1: Stochastic Process & Quantum Mechanics . Taylor e Francis. p. 1ff. ISBN 978-0-7503-0801-4.
• DeWitt-Morette, C. (1972). "Integral do caminho de Feynman: Definição sem procedimento limitante". Comunicações em Física Matemática . 28 (1): 47–67. Bibcode : 1972CMaPh..28 ... 47D . doi : 10.1007 / BF02099371 . MR  0309456 . S2CID  119669964 .
• Dirac, Paul AM (1933). "The Lagrangian in Quantum Mechanics" (PDF) . Physikalische Zeitschrift der Sowjetunion . 3 : 64–72.
• Duru, İ. H .; Kleinert, Hagen (1979). "Solução da integral do caminho para o átomo H" (PDF) . Letras de Física . 84B (2): 185–188. Bibcode : 1979PhLB ... 84..185D . doi : 10.1016 / 0370-2693 (79) 90280-6 . Página visitada em 2007-11-25 .
• Etingof, P (2002). "Geometria e Teoria Quântica de Campos" . MIT OpenCourseWare. Este curso, projetado para matemáticos, é uma introdução rigorosa à teoria quântica de campos perturbativos, usando a linguagem de integrais funcionais.
• Feynman, RP (2005) [1942/1948]. Brown, LM (ed.). Tese de Feynman - Uma Nova Abordagem à Teoria Quântica . World Scientific. Bibcode : 2005ftna.book ..... B . doi : 10.1142 / 5852 . ISBN 978-981-256-366-8. A tese de 1942. Também inclui o artigo de Dirac de 1933 e a publicação de 1948 de Feynman.
• Feynman, RP (1948). "Abordagem Espaço-Temporal à Mecânica Quântica Não Relativística" (PDF) . Avaliações da Física Moderna . 20 (2): 367–387. Bibcode : 1948RvMP ... 20..367F . doi : 10.1103 / RevModPhys.20.367 .
• Feynman, RP; Hibbs, AR (1965). Mecânica Quântica e Integrais de Caminho . Nova York: McGraw-Hill. ISBN 978-0-07-020650-2. A referência histórica, escrita pelo próprio inventor da formulação integral do caminho e por um de seus alunos.
• Feynman, RP; Hibbs, AR ; Styer, DF (2010). Mecânica Quântica e Integrais de Caminho . Mineola, NY: Dover Publications. pp. 29–31. ISBN 978-0-486-47722-0.
• Gell-Mann, Murray (1993). "A maioria das coisas boas". Em Brown, Laurie M .; Rigden, John S. (eds.). Memórias de Richard Feynman . Instituto Americano de Física. ISBN 978-0883188705.
• Glimm, J. & Jaffe, A. (1981). Física Quântica: Um Ponto de Vista Integral Funcional . Nova York: Springer-Verlag. ISBN 978-0-387-90562-4.
• Grosche, Christian & Steiner, Frank (1998). Handbook of Feynman Path Integrals . Springer Tracts in Modern Physics 145. Springer-Verlag. ISBN 978-3-540-57135-3.
• Grosche, Christian (1992). "Uma introdução ao caminho integral de Feynman". arXiv : hep-th / 9302097 .
• Hall, Brian C. (2013). Quantum Theory for Mathematicians . Textos de Pós-Graduação em Matemática. 267 . Springer. doi : 10.1007 / 978-1-4614-7116-5 . ISBN 978-1-4614-7115-8.
• Inomata, Akira; Kuratsuji, Hiroshi; Gerry, Christopher (1992). Integrais de trajetória e estados coerentes de SU (2) e SU (1,1) . Singapura: World Scientific. ISBN 978-981-02-0656-7.
• Janke, W .; Pelster, Axel, eds. (2008). Path Integrals - Novas Tendências e Perspectivas . Anais da 9ª Conferência Internacional. Publicação Científica Mundial. ISBN 978-981-283-726-4.
• Johnson, Gerald W .; Lapidus, Michel L. (2002). A Integral de Feynman e o Cálculo Operacional de Feynman . Oxford Mathematical Monographs. Imprensa da Universidade de Oxford. ISBN 978-0-19-851572-2.
• Klauder, John R. (2010). Uma abordagem moderna para integração funcional . Nova York: Birkhäuser. ISBN 978-0-8176-4790-2.
• Kleinert, Hagen (2004). Integrais de Caminho em Mecânica Quântica, Estatística, Física de Polímeros e Mercados Financeiros (4ª ed.). Singapura: World Scientific. ISBN 978-981-238-107-1.
• MacKenzie, Richard (2000). "Métodos e aplicativos integrais de caminho". arXiv : quant-ph / 0004090 .
• Mazzucchi, S. (2009). Integrais matemáticas de caminho de Feynman e suas aplicações . World Scientific. ISBN 978-981-283-690-8.
• Müller-Kirsten, Harald JW (2012). Introdução à Mecânica Quântica: Equação de Schrödinger e Integral de Caminho (2ª ed.). Singapura: World Scientific.
• Rivers, RJ (1987). Métodos Integrais de Caminho na Teoria Quântica de Campos . Cambridge University Press. ISBN 978-0-521-25979-8.
• Ryder, Lewis H. (1985). Teoria Quântica de Campos . Cambridge University Press. ISBN 978-0-521-33859-2.Livro de leitura altamente legível; introdução ao QFT relativístico para física de partículas.
• Schulman, L. S. (1981). Técnicas e aplicações de integração de caminhos . Nova York: John Wiley & Sons. ISBN 978-0-486-44528-1.
• Simon, B. (1979). Integração Funcional e Física Quântica . Nova York: Academic Press. ISBN 978-0-8218-6941-3.
• Sinha, Sukanya; Sorkin, Rafael D. (1991). "Uma conta de soma de histórias de um experimento EPR (B)" (PDF) . Fundamentos das Letras de Física . 4 (4): 303–335. Bibcode : 1991FoPhL ... 4..303S . doi : 10.1007 / BF00665892 . S2CID  121370426 .
• Tomé, WA (1998). Integrais de caminho em manifolds de grupo . Singapura: World Scientific. ISBN 978-981-02-3355-6. Discute a definição de Integrais de caminho para sistemas cujas variáveis ​​cinemáticas são os geradores de um grupo de Lie real separável e conectado com representações quadradas integráveis ​​irredutíveis.
• Van Vleck, JH (1928). "O princípio da correspondência na interpretação estatística da mecânica quântica" . Anais da Academia Nacional de Ciências dos Estados Unidos da América . 14 (2): 178–188. Bibcode : 1928PNAS ... 14..178V . doi : 10.1073 / pnas.14.2.178 . PMC  1085402 . PMID  16577107 .
• Weinberg, S. (2002) [1995], Foundations , The Quantum Theory of Fields, 1 , Cambridge: Cambridge University Press , ISBN 978-0-521-55001-7
• Zee, A. (21/02/2010). Quantum Field Theory in a Nutshell (segunda edição). Princeton University Press. ISBN 978-0-691-14034-6. Uma ótima introdução a Path Integrals (Capítulo 1) e QFT em geral.
• Zinn Justin, J. (2004). Path Integrals in Quantum Mechanics . Imprensa da Universidade de Oxford. ISBN 978-0-19-856674-8.

links externos

• Integral do caminho na Scholarpedia
• Integrais de caminho em teorias quânticas: um primeiro passo pedagógico
• Uma abordagem matematicamente rigorosa para integrais de caminho perturbativo por meio de animação no YouTube
• Caminhos quânticos infinitos de Feynman | PBS Space Time. 7 de julho de 2017. (Vídeo, 15:48)