Algoritmo rho de Pollard - Pollard's rho algorithm
O algoritmo rho de Pollard é um algoritmo para fatoração de inteiros . Foi inventado por John Pollard em 1975. Ele usa apenas uma pequena quantidade de espaço e seu tempo de execução esperado é proporcional à raiz quadrada do tamanho do menor fator primo do número composto sendo fatorado.
Ideias centrais
O algoritmo é usado para fatorar um número , onde é um fator não trivial. Um modulo polinomial , chamado (por exemplo, ), é usado para gerar uma sequência pseudo-aleatória : Um valor inicial, digamos, 2, é escolhido, e a sequcia continua como , , , etc A sequência está relacionada a uma outra sequência . Como não é conhecida de antemão, essa sequência não pode ser computada explicitamente no algoritmo. No entanto, nele reside a ideia central do algoritmo.
Como o número de valores possíveis para essas sequências é finito, a sequência, que é mod , e a sequência acabarão se repetindo, embora esses valores sejam desconhecidos. Se as sequências se comportassem como números aleatórios, o paradoxo do aniversário implica que o número de antes de ocorrer uma repetição seria esperado , onde é o número de valores possíveis. Portanto, a sequência provavelmente se repetirá muito antes da sequência . Uma vez que uma sequência tem um valor repetido, a sequência vai circular, porque cada valor depende apenas do anterior. Esta estrutura de eventual ciclismo dá origem ao nome "rho algoritmo", devido à semelhança com a forma do carácter grego ρ quando os valores , , etc, são representados como os nós de um gráfico dirigido .
Isso é detectado pelo algoritmo de localização de ciclos de Floyd : dois nós e (ou seja, e ) são mantidos. Em cada etapa, um avança para o próximo nó na sequência e o outro avança dois nós. Depois disso, é verificado se . Se não for 1, isso implica que há uma repetição na sequência (ou seja, isso funciona porque, se for o mesmo que , a diferença entre e é necessariamente um múltiplo de . Embora isso sempre aconteça eventualmente, o maior comum resultante divisor (GCD) é um divisor diferente de 1. Pode ser ele mesmo, já que as duas sequências podem se repetir ao mesmo tempo. Nesse caso (incomum), o algoritmo falha e pode ser repetido com um parâmetro diferente.
Algoritmo
O algoritmo toma como suas entradas n , o inteiro a ser fatorado; e , um polinômio em x módulo computado n . No algoritmo original , mas hoje em dia é mais comum de usar . A saída é um fator não trivial de n ou falha. Ele executa as seguintes etapas:
x ← 2
y ← 2
d ← 1
while d = 1:
x ← g(x)
y ← g(g(y))
d ← gcd(|x - y|, n)
if d = n:
return failure
else:
return d
Aqui x e y corresponde a e na seção sobre a idéia do núcleo. Observe que este algoritmo pode falhar em encontrar um fator não trivial mesmo quando n é composto. Nesse caso, o método pode ser tentado novamente, usando um valor inicial diferente de 2 ou um diferente .
Exemplo de fatoração
Deixe e .
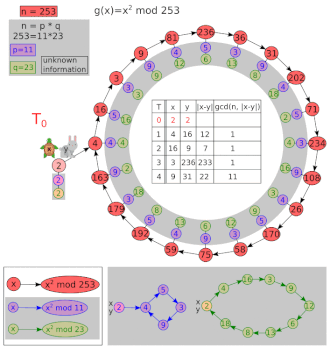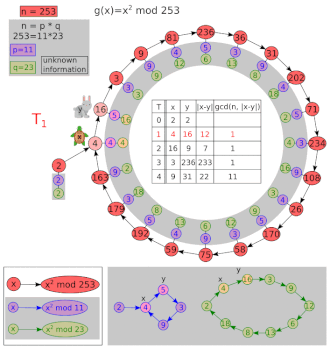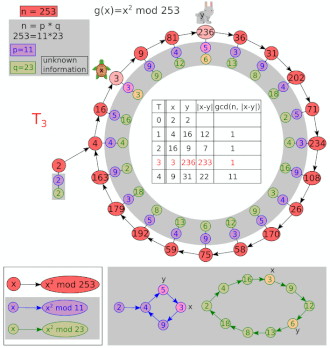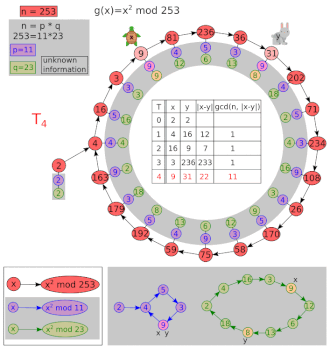
| eu | x | y | GCD (| x - y |, 8051) |
|---|---|---|---|
| 1 | 5 | 26 | 1 |
| 2 | 26 | 7474 | 1 |
| 3 | 677 | 871 | 97 |
| 4 | 7474 | 1481 | 1 |
97 é um fator não trivial de 8051. Valores iniciais diferentes de x = y = 2 podem fornecer o cofator (83) em vez de 97. Uma iteração extra é mostrada acima para deixar claro que y se move duas vezes mais rápido que x . Observe que, mesmo após uma repetição, o GCD pode retornar a 1.
Variantes
Em 1980, Richard Brent publicou uma variante mais rápida do algoritmo rho. Ele usou as mesmas ideias centrais de Pollard, mas um método diferente de detecção de ciclo, substituindo o algoritmo de descoberta de ciclo de Floyd pelo método de descoberta de ciclo de Brent relacionado .
Uma melhoria adicional foi feita por Pollard e Brent. Eles observaram que se , então, também para qualquer número inteiro positivo . Em particular, em vez de calcular a cada etapa, é suficiente definir como o produto de 100 termos consecutivos o módulo e, em seguida, calcular um único . Uma grande aceleração resulta na substituição de passos de 100 gcd por módulo de 99 multiplicações e um único gcd . Ocasionalmente, pode fazer com que o algoritmo falhe ao introduzir um fator repetido, por exemplo, quando é um quadrado. Mas então é suficiente voltar ao termo mdc anterior , onde , e usar o algoritmo ρ regular a partir daí.
Aplicativo
O algoritmo é muito rápido para números com fatores pequenos, mas mais lento nos casos em que todos os fatores são grandes. O sucesso mais notável do algoritmo ρ foi a fatoração do número de Fermat F 8 = 1238926361552897 × 93461639715357977769163558199606896584051237541638188580280321. O algoritmo ρ foi uma boa escolha para F 8 porque o fator principal p = 1238926361552897 é muito menor do que o outro fator. A fatoração levou 2 horas em um UNIVAC 1100/42 .
O exemplo n = 10403 = 101 · 103
Neste exemplo, apenas uma única sequência é calculada, e o gcd é calculado dentro do loop que detecta o ciclo.
Amostra de código C
O exemplo de código a seguir encontra o fator 101 de 10403 com um valor inicial de x = 2.
#include <stdio.h>
#include <stdlib.h>
int gcd(int a, int b)
{
int remainder;
while (b != 0) {
remainder = a % b;
a = b;
b = remainder;
}
return a;
}
int main (int argc, char *argv[])
{
int number = 10403, loop = 1, count;
int x_fixed = 2, x = 2, size = 2, factor;
do {
printf("---- loop %4i ----\n", loop);
count = size;
do {
x = (x * x + 1) % number;
factor = gcd(abs(x - x_fixed), number);
printf("count = %4i x = %6i factor = %i\n", size - count + 1, x, factor);
} while (--count && (factor == 1));
size *= 2;
x_fixed = x;
loop = loop + 1;
} while (factor == 1);
printf("factor is %i\n", factor);
return factor == number ? EXIT_FAILURE : EXIT_SUCCESS;
}
O código acima irá mostrar o progresso do algoritmo, bem como os valores intermediários. A linha de saída final será "fator é 101". O código funcionará apenas para pequenos valores de teste, pois o estouro ocorrerá em tipos de dados inteiros durante o quadrado de x.
Amostra de código Python
from itertools import count
from math import gcd
import sys
number, x = 10403, 2
for cycle in count(1):
y = x
for i in range(2 ** cycle):
x = (x * x + 1) % number
factor = gcd(x - y, number)
if factor > 1:
print("factor is", factor)
sys.exit()
Os resultados
Na tabela a seguir, a terceira e a quarta colunas contêm informações secretas desconhecidas da pessoa que está tentando fatorar pq = 10403. Elas foram incluídas para mostrar como o algoritmo funciona. Começando com x = 2, o algoritmo produz os seguintes números:
| Passo | ||||
|---|---|---|---|---|
| 2 | 2 | 2 | 2 | 0 |
| 5 | 2 | 5 | 2 | 1 |
| 26 | 2 | 26 | 2 | 2 |
| 677 | 26 | 71 | 26 | 3 |
| 598 | 26 | 93 | 26 | 4 |
| 3903 | 26 | 65 | 26 | 5 |
| 3418 | 26 | 85 | 26 | 6 |
| 156 | 3418 | 55 | 85 | 7 |
| 3531 | 3418 | 97 | 85 | 8 |
| 5168 | 3418 | 17 | 85 | 9 |
| 3724 | 3418 | 88 | 85 | 10 |
| 978 | 3418 | 69 | 85 | 11 |
| 9812 | 3418 | 15 | 85 | 12 |
| 5983 | 3418 | 24 | 85 | 13 |
| 9970 | 3418 | 72 | 85 | 14 |
| 236 | 9970 | 34 | 72 | 15 |
| 3682 | 9970 | 46 | 72 | 16 |
| 2016 | 9970 | 97 | 72 | 17 |
| 7087 | 9970 | 17 | 72 | 18 |
| 10289 | 9970 | 88 | 72 | 19 |
| 2594 | 9970 | 69 | 72 | 20 |
| 8499 | 9970 | 15 | 72 | 21 |
| 4973 | 9970 | 24 | 72 | 22 |
| 2799 | 9970 | 72 | 72 | 23 |
O primeiro módulo de repetição 101 é 97 que ocorre na etapa 17. A repetição não é detectada até a etapa 23, quando . Isso faz com que seja , e um fator é encontrado.
Complexidade
Se o número pseudoaleatório que ocorre no algoritmo Pollard ρ fosse um número aleatório real, seguir-se-ia que o sucesso seria alcançado na metade do tempo, pelo paradoxo do aniversário em iterações. Acredita-se que a mesma análise se aplica também ao algoritmo rho real, mas esta é uma afirmação heurística, e uma análise rigorosa do algoritmo permanece aberta.
Veja também
Referências
Leitura adicional
- Katz, Jonathan; Lindell, Yehuda (2007). "Capítulo 8". Introdução à Criptografia Moderna . CRC Press.
- Samuel S. Wagstaff, Jr. (2013). A alegria de fatorar . Providence, RI: American Mathematical Society. pp. 135–138. ISBN 978-1-4704-1048-3.












































