Na geometria plana elementar , a potência de um ponto é um número real que reflete a distância relativa de um determinado ponto a um determinado círculo. Foi introduzido por Jakob Steiner 1826.
Especificamente, a potência de um ponto em relação a um círculo com centro e raio é definida por






Se está fora do círculo, então ,
se está no círculo, então e
se está dentro do círculo, então .






Devido ao teorema de Pitágoras, o número tem os significados geométricos simples mostrados no diagrama: Para um ponto fora do círculo é a distância tangencial ao quadrado do ponto ao círculo .






Pontos com igual poder, isolinhas de , são círculos concêntricos a um círculo .


Steiner usou o poder de um ponto para provas de várias declarações sobre círculos, por exemplo:
- Determinação de um círculo, que cruza quatro círculos com o mesmo ângulo.
- Resolvendo o problema de Apolônio
- Construção dos círculos Malfatti : Para um determinado triângulo, determine três círculos, que se tocam e dois lados do triângulo cada um.
-
Versão esférica do problema de Malfatti: o triângulo é esférico.
As ferramentas essenciais para investigações em círculos são o eixo radical de dois círculos e o centro radical de três círculos.
O diagrama de potência de um conjunto de círculos divide o plano em regiões nas quais o círculo que minimiza a potência é constante.
De maneira mais geral, o matemático francês Edmond Laguerre definiu a potência de um ponto em relação a qualquer curva algébrica de maneira semelhante.
Propriedades geométricas
Além das propriedades mencionadas no lead, existem outras propriedades:
Círculo ortogonal

Círculo ortogonal (verde)
Para qualquer ponto fora do círculo, há dois pontos tangentes no círculo , que têm distância igual a . Daí o círculo com centro através de passes , também, e intersecção ortogonal:










- O círculo com centro e raio cruza o círculo ortogonal .




Ângulo entre dois círculos
Se o raio do círculo centrado em for diferente de, obtém-se o ângulo de intersecção entre os dois círculos aplicando a Lei dos cossenos (veja o diagrama):






( e são normais para as tangentes do círculo.)


Se está dentro do círculo azul, então e é sempre diferente de .




Se o ângulo é dado, então obtém-se o raio resolvendo a equação quadrática


-
 .
.
Teorema de secantes de intersecção, teorema de acordes de intersecção

Secante-, teorema do acorde
Para o teorema das secantes que se cruzam e o teorema do acorde, o poder de um ponto desempenha o papel de um invariante :
-
Teorema de interseção de secantes : Para um ponto fora de um círculo e os pontos de interseção de uma linha secante com a seguinte afirmação é verdadeira :, portanto, o produto é independente da linha . Se é tangente então e a afirmação é o teorema tangente-secante .









-
Teorema dos acordes de interseção : Para um ponto dentro de um círculoe os pontosdeinterseçãode uma linha secantecoma seguinte afirmação é verdadeira:, portanto, o produto é independente da linha.







Eixo radical
Let Ser um ponto e dois círculos não concêntricos com centros e raios . O ponto tem poder em relação ao círculo . O conjunto de todos os pontos com é uma linha chamada eixo radical . Ele contém possíveis pontos comuns dos círculos e é perpendicular à linha .










Teorema das secantes, teorema dos acordes: prova comum

Secante- / teorema do acorde: prova
Ambos os teoremas, incluindo o teorema tangente-secante , podem ser provados uniformemente:
Let Ser um ponto, um círculo com a origem como seu centro e um vetor unitário arbitrário . Os parâmetros de possíveis pontos comuns de linha (através ) e círculo podem ser determinados inserindo a equação parmétrica na equação do círculo:








Do teorema de Vieta encontra-se:
-
 . (independente de !)
. (independente de !)
 é o poder de respeitar o círculo .
é o poder de respeitar o círculo .


Por causa de um obtém a seguinte declaração para os pontos :


-
 , se estiver fora do círculo,
, se estiver fora do círculo,
-
 , se estiver dentro do círculo ( tem sinais diferentes!).
, se estiver dentro do círculo ( tem sinais diferentes!).

No caso da linha é uma tangente e o quadrado da distância tangencial do ponto ao círculo .





Pontos de semelhança, poder comum de dois círculos
Pontos de semelhança
Os pontos de semelhança são uma ferramenta essencial para as investigações de Steiner sobre círculos.
Dados dois círculos
-
 .
.
A homothety ( similaridade ) , que mapeia para trechos (solavancos) raio a e tem o seu centro na linha , pois . Se o centro estiver entre o fator de escala é . No outro caso . Em qualquer caso:












-
 .
.
Inserindo e resolvendo para rendimentos:


-
 .
.

Pontos de semelhança de dois círculos: vários casos
Apontar

é chamado de ponto de semelhança exterior e

ponto de semelhança interno .
No caso de alguém conseguir .
No caso de : é o ponto no infinito da linha e é o centro de .
No caso dos círculos se tocarem no ponto interno (ambos os círculos do mesmo lado da linha tangente comum).
No caso dos círculos se tocarem no ponto externo (ambos os círculos em lados diferentes da linha tangente comum).











Além disso:
- Se os círculos estiverem disjuntos (os discos não têm pontos em comum), as tangentes comuns externas encontram-se em e as internas em .


- Se um círculo estiver contido no outro , os pontos ficarão dentro de ambos os círculos.

- Os pares são conjugados harmônicos projetivos : sua razão cruzada é .


O teorema de Monge afirma: Os pontos de semelhança externos de três círculos disjuntos encontram-se em uma linha.
Poder comum de dois círculos

Pontos de semelhança de dois círculos e seu poder comum
Sejam dois círculos, seu ponto de semelhança externo e uma linha através , que encontra os dois círculos em quatro pontos . Da propriedade de definição do ponto obtém-se








e do teorema secante (veja acima) as duas equações

Combinando essas três equações resulta:


Por isso:
-
 (independente da linha !).
(independente da linha !).
A declaração analógica para o ponto de semelhança interno também é verdadeira.

Os invariantes são chamados por Steiner de poder comum dos dois círculos ( gemeinschaftliche Potenz der beiden Kreise bezüglich ihrer Ähnlichkeitspunkte ).

Os pares e de pontos são pontos anti-homólogos . Os pares e são homólogos .




Determinação de um círculo, que é tangente a dois círculos
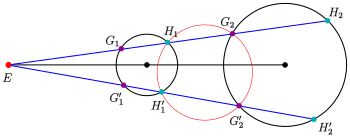
Poder comum de dois círculos: aplicação

Círculos tangentes a dois círculos
Para uma segunda secante por meio de :


Do teorema secante obtém-se:
- Os quatro pontos ficam em um círculo.

E analogamente:
- Os quatro pontos também estão em um círculo.

Como as linhas radicais de três círculos se encontram no radical (ver: linha radical do artigo), obtém-se:
- As secantes se encontram no eixo radical dos dois círculos dados.

Movendo a secante inferior (veja o diagrama) em direção à superior, o círculo vermelho se torna um círculo, que é tangente a ambos os círculos dados. O centro do círculo tangente é a interceptação das linhas . As secantes tornam-se tangentes nos pontos . As tangentes se interceptam na linha radical (no diagrama amarelo).




Considerações semelhantes geram o segundo círculo tangente, que encontra os círculos dados nos pontos (ver diagrama).

Todos os círculos tangentes aos círculos dados podem ser encontrados por linhas variadas .

- Posições dos centros

Círculos tangentes a dois círculos
Se é o centro e o raio do círculo, que é tangente aos círculos dados nos pontos , então:





Portanto: os centros estão em uma hipérbole com
- focos ,

- distância dos vértices ,

- centro é o centro de ,


- excentricidade linear e

-
 .
.
Considerações sobre os círculos tangentes externos levam ao resultado analógico:
Se é o centro e o raio do círculo, que é tangente aos círculos dados nos pontos , então:





Os centros estão na mesma hipérbole, mas no ramo direito.
Veja também Problema de Apolônio .

Potência de um ponto em relação a uma esfera
Poder em relação a uma esfera
A ideia do poder de um ponto em relação a um círculo pode ser estendida a uma esfera. Os teoremas das secantes e acordes também são verdadeiros para uma esfera e podem ser provados literalmente como no caso do círculo.
Produto Darboux
O poder de um ponto é um caso especial do produto Darboux entre dois círculos, que é dado por

onde A 1 e A 2 são os centros dos dois círculos er 1 e r 2 são seus raios. A potência de um ponto surge no caso especial em que um dos raios é zero.
Se os dois círculos forem ortogonais, o produto Darboux desaparece.
Se os dois círculos se cruzam, então seu produto Darboux é

onde φ é o ângulo de interseção (ver seção círculo ortogonal ).
Teorema de Laguerre
Laguerre definido a potência de um ponto P com respeito a uma curva algébrica de grau n ser o produto das distâncias do ponto para as intersecções de um círculo que passa pelo ponto com a curva, dividido pelo N ° de potência do diâmetro d . Laguerre mostrou que este número é independente do diâmetro ( Laguerre 1905 ). No caso em que a curva algébrica é um círculo, isso não é exatamente o mesmo que a potência de um ponto em relação a um círculo definido no resto deste artigo, mas difere dele por um fator de d 2 .
Referências
-
Coxeter, HSM (1969), Introdução à Geometria (2ª ed.), Nova York: Wiley.
-
Darboux, Gaston (1872), "Sur les relações entre les groupes de points, de cercles et de sphéres dans le plan et dans l'espace", Annales Scientifiques de l'École Normale Supérieure , 1 : 323-392.
-
Laguerre, Edmond (1905), Oeuvres de Laguerre: Géométrie (em francês), Gauthier-Villars et fils, p. 20
-
Steiner, Jakob (1826), "Einige geometrische Betrachtungen", Journal für die reine und angewandte Mathematik , 1 : 161-184.
-
Berger , Marcel (1987), Geometry I , Springer , ISBN 978-3-540-11658-5
Leitura adicional
-
Ogilvy CS (1990), Excursions in Geometry , Dover Publications, pp. 6-23 , ISBN 0-486-26530-7
-
Coxeter HSM , Greitzer SL (1967), Geometry Revisited , Washington : MAA , pp. 27-31, 159-160, ISBN 978-0-88385-619-2
-
Johnson RA (1960), Advanced Euclidean Geometry: Um tratado elementar sobre a geometria do triângulo e do círculo (reimpressão da edição de 1929 por Houghton Miflin ed.), Nova York: Dover Publications, pp. 28-34, ISBN 978-0-486-46237-0
links externos





















































































































