Aceleração adequada - Proper acceleration

Mapa e visualizações do viajante de uma aceleração adequada de um gee após o repouso por um ano.

Espaço-tempo do viajante para uma viagem de ida e volta com aceleração constante.

Na teoria da relatividade , a aceleração adequada é a aceleração física (ou seja, a aceleração mensurável como por um acelerômetro ) experimentada por um objeto. É, portanto, a aceleração relativa a um observador em queda livre , ou inercial, que está momentaneamente em repouso em relação ao objeto que está sendo medido. A gravidade, portanto, não causa a aceleração adequada, uma vez que a gravidade atua sobre o observador inercial do qual qualquer aceleração adequada deve se afastar. Um corolário é que todos os observadores inerciais sempre têm uma aceleração adequada de zero.

A aceleração adequada contrasta com a aceleração por coordenadas , que depende da escolha dos sistemas de coordenadas e, portanto, da escolha dos observadores (ver três acelerações na relatividade especial ).

Nas coordenadas inerciais padrão da relatividade especial, para o movimento unidirecional, a aceleração adequada é a taxa de variação da velocidade adequada em relação ao tempo coordenado.

Em um referencial inercial no qual o objeto está momentaneamente em repouso, o vetor 3 de aceleração apropriado, combinado com um componente de tempo zero, produz a aceleração quatro do objeto , o que torna a magnitude da aceleração apropriada invariante de Lorentz . Assim, o conceito é útil: (i) com sistemas de coordenadas aceleradas, (ii) em velocidades relativísticas, e (iii) em espaço-tempo curvo.

Em um foguete em aceleração após o lançamento, ou mesmo em um foguete no pórtico, a aceleração adequada é a aceleração sentida pelos ocupantes, e que é descrita como força-g (que não é uma força, mas sim uma aceleração; consulte esse artigo para mais discussão sobre aceleração adequada) entregue apenas pelo veículo. A "aceleração da gravidade" ("força da gravidade") nunca contribui para a aceleração adequada em nenhuma circunstância e, portanto, a aceleração adequada sentida pelos observadores em pé no solo é devido à força mecânica do solo , não devido à "força "ou" aceleração "da gravidade. Se o solo for removido e o observador cair em queda livre, o observador experimentará aceleração coordenada, mas nenhuma aceleração adequada e, portanto, nenhuma força g. Geralmente, os objetos em tal queda ou geralmente em qualquer caminho balístico (também chamado de movimento inercial), incluindo objetos em órbita, não experimentam nenhuma aceleração adequada (negligenciando pequenas acelerações de maré para caminhos inerciais em campos gravitacionais). Este estado também é conhecido como "gravidade zero" ("zero-g") ou "queda livre" e produz uma sensação de ausência de peso .

A aceleração adequada se reduz à aceleração coordenada em um sistema de coordenadas inercial no espaço-tempo plano (ou seja, na ausência de gravidade), desde que a magnitude da velocidade adequada do objeto (momento por unidade de massa) seja muito menor do que a velocidade da luz c . Somente em tais situações a aceleração coordenada é inteiramente sentida como uma força g (ou seja, uma aceleração adequada, também definida como aquela que produz peso mensurável).

Em situações em que a gravitação está ausente, mas o sistema de coordenadas escolhido não é inercial, mas é acelerado com o observador (como o referencial acelerado de um foguete em aceleração ou um quadro fixado em objetos em uma centrífuga), então as forças g e as correspondentes acelerações apropriadas sentidas pelos observadores nesses sistemas de coordenadas são causadas pelas forças mecânicas que resistem ao seu peso em tais sistemas. Esse peso, por sua vez, é produzido por forças fictícias ou "forças inerciais" que aparecem em todos esses sistemas de coordenadas aceleradas, de maneira semelhante ao peso produzido pela "força da gravidade" em sistemas onde os objetos são fixos no espaço em relação para o corpo gravitante (como na superfície da Terra).

A força (mecânica) total calculada para induzir a aceleração adequada em uma massa em repouso em um sistema de coordenadas que tem uma aceleração adequada, via lei de Newton F = m a , é chamada de força adequada . Como visto acima, a força adequada é igual à força de reação oposta que é medida como o "peso operacional" de um objeto (ou seja, seu peso medido por um dispositivo como uma balança de mola, no vácuo, no sistema de coordenadas do objeto). Assim, a força adequada em um objeto é sempre igual e oposta ao seu peso medido.

Exemplos

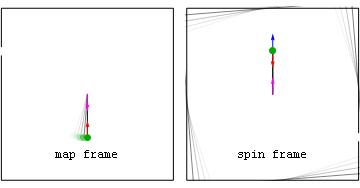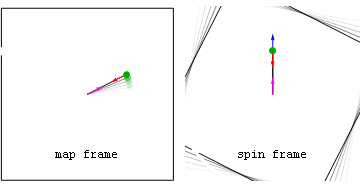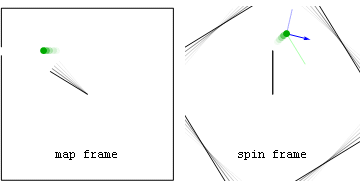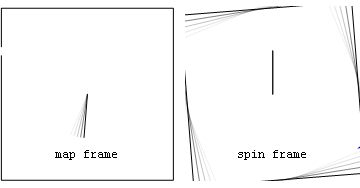
Ao segurar em um carrossel que gira em velocidade angular constante, um observador experimenta uma aceleração adequada radialmente para dentro ( centrípeta ) devido à interação entre a pega e a mão do observador. Isso cancela a aceleração geométrica radialmente para fora associada com seu quadro de coordenadas giratórias . Esta aceleração externa (da perspectiva do referencial giratório) se tornará a aceleração coordenada quando eles se soltarem, fazendo com que voem ao longo de um caminho de aceleração adequada zero ( geodésico ). Os observadores não acelerados, é claro, em sua estrutura simplesmente veem suas acelerações adequadas e coordenadas iguais desaparecerem quando eles se soltam.

Animação: perda de aderência em um carrossel
Mapeie e gire as perspectivas das acelerações adequadas (vermelho) e geométricas (azul) para um objeto liberado de um carrossel. Da perspectiva do quadro do mapa, o que é perigoso é sua velocidade tangencial. Da perspectiva do quadro de rotação, o perigo pode residir na aceleração geométrica.

Da mesma forma, estando em um planeta sem rotação (e na Terra para fins práticos), os observadores experimentam uma aceleração para cima apropriada devido à força normal exercida pela Terra na sola de seus sapatos. Isso cancela a aceleração geométrica para baixo devido à escolha do sistema de coordenadas (uma chamada estrutura de concha). Essa aceleração descendente torna-se coordenada se eles inadvertidamente pularem de um penhasco em uma trajetória de aceleração adequada zero (geodésica ou quadro de chuva).

Animação: bola que rola de um penhasco

A chuva e a concha enquadram as perspectivas das acelerações adequadas (vermelho) e geométricas (azul) de um objeto que rola de um penhasco. Nota: A perspectiva do quadro de chuva, ao invés de ser a de uma gota de chuva, é mais parecida com a de um saltador de cama elástica cuja trajetória termina no momento em que a bola atinge a borda do penhasco. A perspectiva da estrutura da concha pode ser familiar para os habitantes de planetas que contam minuto a minuto com as acelerações físicas ascendentes de seu ambiente, para protegê-los daquela aceleração geométrica devido ao espaço-tempo curvo. Não é de admirar que os ambientes de microgravidade possam parecer assustadores a princípio.

Observe que as acelerações geométricas (devido ao termo de conexão na derivada covariante do sistema de coordenadas abaixo) agem em cada grama de nosso ser , enquanto as acelerações adequadas são geralmente causadas por uma força externa. Cursos introdutórios de física geralmente tratam a aceleração para baixo (geométrica) da gravidade como devida a uma força proporcional à massa . Isso, junto com a evitação diligente de quadros não acelerados, permite que eles tratem a aceleração adequada e coordenada como a mesma coisa.

Mesmo assim, se um objeto mantiver uma aceleração adequada constante a partir do repouso por um período prolongado no espaço-tempo plano, os observadores no quadro de repouso verão a aceleração das coordenadas do objeto diminuir à medida que sua velocidade coordenada se aproxima da velocidade da luz. A taxa na qual a velocidade própria do objeto aumenta, no entanto, permanece constante.

Animação: viagem de alta velocidade para cima e para baixo

Perspectiva do quadro do mapa das acelerações / desacelerações adequadas (vermelho) e coordenadas (verde) na direção vertical. Aqui, nosso objeto primeiro acelera para cima por um período de tempo de 2 * c / α em relógios viajantes, onde c é a velocidade da luz e α é a magnitude da aceleração adequada (vermelha). Esta primeira etapa leva cerca de 2 anos se a magnitude da aceleração for de cerca de 1 g. Em seguida, acelera para baixo (primeiro desacelerando e depois acelerando) ao longo do dobro desse período, seguido por uma desaceleração 2 * c / α para cima para retornar à altura original. Observe que a aceleração coordenada (verde) é significativa apenas durante os segmentos de baixa velocidade desta viagem.

Assim, a distinção entre aceleração adequada e aceleração coordenada permite rastrear a experiência de viajantes acelerados a partir de várias perspectivas não newtonianas. Essas perspectivas incluem aquelas de sistemas de coordenadas aceleradas (como um carrossel), de altas velocidades (onde os tempos adequados e coordenados diferem) e de espaço-tempo curvo (como aquele associado à gravidade na Terra).

Aplicações clássicas

Em baixas velocidades nos sistemas de coordenadas inerciais da física newtoniana , a aceleração adequada simplesmente é igual à aceleração de coordenadas a = d ² x / dt ² . Conforme revisado acima, no entanto, ele difere da aceleração coordenada se alguém escolher (contra o conselho de Newton) descrever o mundo da perspectiva de um sistema de coordenadas acelerado como um veículo motorizado acelerando do repouso ou uma pedra sendo girada em um estilingue. Se alguém decidir reconhecer que a gravidade é causada pela curvatura do espaço-tempo (veja abaixo), a aceleração adequada difere da aceleração coordenada em um campo gravitacional .

Por exemplo, um objeto sujeito a aceleração física ou adequada a _o será visto por observadores em um sistema de coordenadas em aceleração constante um _quadro para ter aceleração de coordenadas:

${\ displaystyle {\ vec {a}} _ {acc} = {\ vec {a}} _ {o} - {\ vec {a}} _ {frame}}$.

Portanto, se o objeto está acelerando com o quadro, os observadores fixos no quadro não verão nenhuma aceleração.

Animação: dirigindo de bloco em bloco
Perspectivas do mapa e do quadro do carro das acelerações físicas (vermelho) e geométricas (azul) de um carro que vai de uma placa de pare a outra. Nesta ilustração, o carro acelera após um sinal de pare até o meio do quarteirão, ponto em que o motorista sai imediatamente do acelerador e pisa no freio para fazer a próxima parada.

Da mesma forma, um objeto submetido a aceleração física ou adequada a _o será visto por observadores em um quadro girando com velocidade angular ω para ter aceleração coordenada:

${\ displaystyle {\ vec {a}} _ {rot} = {\ vec {a}} _ {o} - {\ vec {\ omega}} \ times ({\ vec {\ omega}} \ times {\ vec {r}}) - 2 {\ vec {\ omega}} \ times {\ vec {v}} _ {rot} - {\ frac {d {\ vec {\ omega}}} {dt}} \ times {\ vec {r}}}$.

Na equação acima, existem três termos de aceleração geométrica no lado direito. O primeiro termo de "aceleração centrífuga" depende apenas da posição radial r e não da velocidade de nosso objeto, o segundo termo de "aceleração de Coriolis" depende apenas da velocidade do objeto no quadro rotativo v _rot, mas não de sua posição, e o terceiro " O termo "aceleração de Euler" depende apenas da posição e da taxa de variação da velocidade angular do quadro.

Exemplo newtoniano: estilingue de velocidade constante

Mapeie e gire as perspectivas das acelerações e forças associadas a uma pedra lançada após ser girada em uma corda sem massa. As forças na pedra incluem a força centrípeta para dentro (vermelha) vista em ambos os quadros, bem como a força geométrica (azul) vista no quadro de rotação. Antes de a pedra ser liberada, a força geométrica azul é puramente centrífuga (apontando radialmente para fora), enquanto após a liberação a força geométrica é uma soma dos componentes centrífugos e de Coriolis. Observe que, após a liberação no quadro de rotação, o componente centrífugo (azul claro) é sempre radial, enquanto o componente de Coriolis (verde) é sempre perpendicular à velocidade do quadro de rotação. Também é vista em ambos os quadros a força no ponto de ancoragem da corda (magenta) causada pela ação-reação da 3ª Lei de Newton à força centrípeta na pedra. Antes do lançamento do projétil As seguintes análises alternativas do movimento antes de a pedra ser liberada consideram apenas as forças que atuam na direção radial. Ambas as análises prevêem que a tensão da corda T = mv 2 / r . Por exemplo, se o raio da funda for r = 1 metro, a velocidade da pedra no quadro do mapa é v = 25 metros por segundo e a massa da pedra m = 0,2 quilograma, então a tensão na corda será 125 newtons. História do quadro do mapa antes do lançamento ${\ displaystyle -T_ {centrípeto} = \ Sigma F_ {radial} = ma_ {radial} = - m {\ frac {v ^ {2}} {r}}.}$ Aqui, a pedra é continuamente acelerada para dentro de modo a seguir um caminho circular de raio r. A aceleração radial para dentro de um radial = v 2 / r é causada por uma única força centrípeta desequilibrada T. O fato de a força de tensão ser desequilibrada significa que, neste quadro, a força centrífuga (radialmente para fora) na pedra é zero . Gire a história do frame antes do lançamento ${\ displaystyle m {\ frac {v ^ {2}} {r}} - T_ {centrípeto} = \ Sigma F_ {rot} = ma_ {rot} = 0.}$ Da perspectiva do quadro de rotação, pode-se dizer que a pedra experimenta forças centrípetas internas ( T ) e centrífugas externas ( mv 2 / r ) equilibradas , que resultam em nenhuma aceleração da perspectiva desse quadro . Ao contrário da força centrípeta, a força centrífuga dependente da estrutura atua em cada pedacinho da pedra circulante, da mesma forma que a gravidade atua em cada grama de você. Além disso, a magnitude da força centrífuga é proporcional à massa da pedra de forma que, se permitisse que causasse aceleração, a aceleração seria independente da massa. Após o lançamento do projétil Depois que a pedra é liberada, no quadro de rotação as forças centrípeta e de Coriolis agem de forma deslocalizada em todas as partes da pedra com acelerações que são independentes da massa da pedra. Em comparação, no quadro do mapa, após o lançamento, nenhuma força está agindo no projétil.

Em cada um desses casos, a aceleração física ou adequada difere da aceleração por coordenadas porque a última pode ser afetada por sua escolha do sistema de coordenadas, bem como por forças físicas agindo sobre o objeto. Esses componentes da aceleração coordenada não causados ​​por forças físicas (como contato direto ou atração eletrostática) são frequentemente atribuídos (como no exemplo newtoniano acima) a forças que: (i) atuam em cada grama do objeto, (ii) causam massa- acelerações independentes e (iii) não existem de todos os pontos de vista. Tais forças geométrico (ou inadequadas) incluem Coriolis forças, Euler forças, forças-g , as forças centrífugas e (como podemos ver abaixo) de gravidade das forças bem.

Visto de uma fatia plana do espaço-tempo

Dinâmica de quadro adequado no espaço-tempo (1 + 1) D.

As relações da aceleração adequada para coordenar a aceleração em uma fatia especificada do espaço-tempo plano seguem da equação métrica do espaço plano de Minkowski ( c d τ ) ² = ( c d t ) ² - (d x ) ² . Aqui, um único referencial de parâmetros e relógios sincronizados define a posição xe o tempo t do mapa respectivamente, os relógios do objeto em viagem definem o tempo adequado τ , e o "d" precedendo uma coordenada significa mudança infinitesimal. Essas relações permitem enfrentar vários problemas de "engenharia de qualquer velocidade", embora apenas do ponto de vista de um observador cujo quadro de mapa estendido define a simultaneidade.

Aceleração em (1 + 1) D

Este gráfico mostra como uma espaçonave capaz de aceleração de 1 g (10 m / s ² ou cerca de 1,0 ano-luz por ano ao quadrado) por 100 anos pode impulsionar uma viagem a quase qualquer lugar no universo visível e de volta em uma vida.

No caso unidirecional, isto é, quando a aceleração do objeto é paralela ou antiparalela à sua velocidade na fatia do espaço-tempo do observador, a aceleração adequada α e a aceleração coordenada a estão relacionadas através do fator de Lorentz γ por α = γ ³ a . Conseqüentemente, a mudança na velocidade apropriada w = dx / dτ é a integral da aceleração apropriada ao longo do tempo do mapa t, isto é, Δ w = α Δ t para α constante . Em baixas velocidades, isso se reduz à relação bem conhecida entre velocidade coordenada e tempos de mapa de aceleração coordenada, ou seja, Δ v = a Δ t .

Para aceleração própria unidirecional constante, relações semelhantes existem entre a rapidez η e o tempo próprio decorrido Δ τ , bem como entre o fator de Lorentz γ e a distância percorrida Δ x . Para ser específico:

${\ displaystyle \ alpha = {\ frac {\ Delta w} {\ Delta t}} = c {\ frac {\ Delta \ eta} {\ Delta \ tau}} = c ^ {2} {\ frac {\ Delta \ gamma} {\ Delta x}}}$,

onde os vários parâmetros de velocidade estão relacionados por

${\ displaystyle \ eta = \ sinh ^ {- 1} \ left ({\ frac {w} {c}} \ right) = \ tanh ^ {- 1} \ left ({\ frac {v} {c}} \ right) = \ pm \ cosh ^ {- 1} \ left (\ gamma \ right)}$.

Essas equações descrevem algumas consequências de viagens aceleradas em alta velocidade. Por exemplo, imagine uma nave espacial que pode acelerar seus passageiros a "1 gee" (10 m / s ² ou cerca de 1,0 ano-luz por ano ao quadrado) na metade do caminho para seu destino e, em seguida, desacelerá-los a "1 gee" pela metade restante. para fornecer gravidade artificial semelhante à da Terra do ponto A ao ponto B no menor tempo possível. Para uma distância de mapa de Δ x _AB , a primeira equação acima prevê um fator de Lorentz de ponto médio (acima de seu valor de repouso unitário) de γ _mid = 1 + α (Δ x _AB / 2) / c ² . Portanto, o tempo de ida e volta nos relógios viajantes será Δ τ = 4 ( c / α ) cosh ⁻¹ ( γ _mid ), durante o qual o tempo decorrido nos relógios de mapa será Δ t  = 4 ( c / α ) sinh [cosh ⁻¹ ( γ _mid )].

Esta nave espacial imaginada poderia oferecer viagens de ida e volta para Proxima Centauri durando cerca de 7,1 anos viajantes (~ 12 anos nos relógios terrestres), viagens de ida e volta ao buraco negro central da Via Láctea de cerca de 40 anos (~ 54.000 anos decorridos em relógios terrestres), e viagens de ida e volta para a Galáxia de Andrômeda com duração de cerca de 57 anos (mais de 5 milhões de anos nos relógios terrestres). Infelizmente, sustentar a aceleração de 1 g por anos é mais fácil de dizer do que fazer, conforme ilustrado pela carga útil máxima para lançar taxas de massa mostradas na figura à direita.

Animação: viagem de ida e volta para uma estrela a 6,9 l de distância

Perspectivas do mapa e do viajante de uma viagem de ida e volta com aceleração adequada constante de 1 g (seta vermelha no quadro do viajante) entre o sol (amarelo) e uma estrela hipotética (ciano) a 6,9 anos-luz de distância. Proxima Centauri (laranja) 4 anos-luz do sol é mostrado em laranja no canto superior esquerdo. De cada perspectiva, um ano deve decorrer a cada dois segundos ou a cada 100 / 17,4 quadros. Depois de cada viagem de ida e volta, os pilotos deste ônibus espacial terão envelhecido apenas a metade dos colegas estacionados na Terra. Esta é a dilatação do tempo em ação. Outras diferenças incluem as mudanças de distância entre estrelas em movimento, vistas no quadro do viajante. Esta é a contração do comprimento em ação. A aceleração coordenada (verde) vista no quadro do mapa só é significativa no ano antes e depois de cada lançamento, enquanto a aceleração adequada (vermelho) sentida pelo viajante é significativa durante a viagem. Observe também o traço de um sinal de luz iniciado a partir de cada ponto de lançamento, mas 0,886 anos no mapa após o lançamento. Este pulso atinge o viajante no ponto médio da viagem para lembrá-lo de começar a desaceleração. No quadro do mapa, Proxima Centauri vê o pulso de rotação antes da estrela de destino, mas o inverso é verdadeiro no quadro do viajante. Isso é relativa simultaneidade em ação. No entanto, ambos os observadores concordam sobre a sequência de eventos ao longo de qualquer linha de mundo semelhante ao tempo.

Em espaço-tempo curvo

Na linguagem da relatividade geral , os componentes do quatro vetor A de aceleração de um objeto (cuja magnitude é a aceleração adequada) estão relacionados aos elementos da quatro velocidades por meio de uma derivada covariante D em relação ao tempo adequado τ:

${\ displaystyle A ^ {\ lambda}: = {\ frac {DU ^ {\ lambda}} {d \ tau}} = {\ frac {dU ^ {\ lambda}} {d \ tau}} + \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu}}$

Aqui, U é a velocidade de quatro do objeto e Γ representa os 64 coeficientes de conexão do sistema de coordenadas ou símbolos de Christoffel . Observe que os índices gregos assumem quatro valores possíveis, a saber, 0 para o eixo do tempo e 1-3 para os eixos de coordenadas espaciais, e que os índices repetidos são usados ​​para indicar a soma de todos os valores desse índice. Trajetórias com aceleração adequada zero são chamadas de geodésicas .

O lado esquerdo deste conjunto de quatro equações (uma de cada para os valores semelhantes ao tempo e três semelhantes ao espaço do índice λ) é o vetor 3 de aceleração adequada do objeto combinado com um componente de tempo nulo, visto do ponto de vista de uma referência ou sistema de coordenadas do guarda-livros no qual o objeto está em repouso. O primeiro termo do lado direito lista a taxa na qual os componentes do tipo temporal (energia / mc ) e do tipo espacial (momentum / m ) das quatro velocidades U do objeto mudam, por unidade de tempo τ em relógios viajantes.

Vamos resolver para o primeiro termo à direita, pois em baixas velocidades seus componentes espaciais representam a aceleração das coordenadas. Mais geralmente, quando o primeiro termo vai para zero, a aceleração das coordenadas do objeto vai para zero. Isso produz ...

${\ displaystyle {\ frac {dU ^ {\ lambda}} {d \ tau}} = A ^ {\ lambda} - \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu}}$.

Assim, como exemplificado com as duas primeiras animações acima, a aceleração coordenada vai para zero sempre que a aceleração adequada é exatamente cancelada pelo termo de conexão (ou aceleração geométrica ) na extrema direita. Cuidado: Este termo pode ser uma soma de até dezesseis termos dependentes de velocidade e posição separados, uma vez que os índices repetidos μ e ν são por convenção somados sobre todos os pares de seus quatro valores permitidos.

Força e equivalência

A equação acima também oferece alguma perspectiva sobre as forças e o princípio da equivalência . Considere as coordenadas locais do guarda-livros para a métrica (por exemplo, uma tétrade Lorentz local como aquela sobre a qual os sistemas de posicionamento global fornecem informações) para descrever o tempo em segundos e o espaço em unidades de distância ao longo de eixos perpendiculares. Se multiplicarmos a equação acima pela massa de repouso do objeto em viagem m, e dividirmos pelo fator de Lorentz γ  = d t / d τ , os componentes espaciais expressam a taxa de mudança de momento para esse objeto da perspectiva das coordenadas usadas para descrever a métrica .

Isso, por sua vez, pode ser dividido em partes devido aos componentes geométricos adequados de aceleração e força. Se ainda multiplicarmos o componente semelhante ao tempo pela velocidade da luz c , e definirmos a velocidade coordenada como v  = d x / d t , obteremos uma expressão para a taxa de mudança de energia também:

${\ displaystyle {\ frac {dE} {dt}} = {\ vec {v}} \ cdot {\ frac {d {\ vec {p}}} {dt}}}$(semelhante ao tempo) e (semelhante ao espaço).${\ displaystyle {\ frac {d {\ vec {p}}} {dt}} = \ Sigma {\ vec {f_ {o}}} + \ Sigma {\ vec {f_ {g}}} = m ({ \ vec {a_ {o}}} + {\ vec {a_ {g}}})}$

Aqui, a _o é uma aceleração devido às forças adequadas e a _g é, por padrão, uma aceleração geométrica que vemos aplicada ao objeto por causa de nossa escolha do sistema de coordenadas. Em baixas velocidades essas acelerações combinam para gerar uma aceleração de coordenadas como uma = d ² x / d t ² , enquanto que para o movimento unidireccional , a qualquer velocidade uma _o 's magnitude é que a aceleração correcta α como na secção acima onde α  = γ ³ a quando a _g é zero. Em geral, expressar essas acelerações e forças pode ser complicado.

No entanto, se usarmos essa análise para descrever o coeficiente de conexão (Γ) termo acima em termos de forças geométricas, então o movimento dos objetos do ponto de vista de qualquer sistema de coordenadas (pelo menos em baixas velocidades) pode ser visto como localmente newtoniano. Isso já é uma prática comum, por exemplo, com força centrífuga e gravidade. Assim, o princípio de equivalência estende a utilidade local das leis de Newton para sistemas de coordenadas aceleradas e além.

Moradores da superfície de um planeta

Para observadores de baixa velocidade mantidos em um raio fixo a partir do centro de um planeta ou estrela esférico, a aceleração coordenada de uma _concha está aproximadamente relacionada à aceleração adequada a _o por:

${\ displaystyle {\ vec {a}} _ {shell} = {\ vec {a}} _ {o} - {\ sqrt {\ frac {r} {r-r_ {s}}}} {\ frac { GM} {r ^ {2}}} {\ hat {r}}}$

onde o raio de Schwarzschild do planeta ou estrela r _s = 2GM / c ² . Conforme o raio do nosso observador de casca se aproxima do raio de Schwarzschild, a aceleração adequada a _o necessária para evitar que ele caia torna-se intolerável.

Por outro lado, para r >> r _s , uma força adequada para cima de apenas GMm / r ² é necessária para evitar que se acelere para baixo. Na superfície da Terra, isso se torna:

${\ displaystyle {\ vec {a}} _ {shell} = {\ vec {a}} _ {o} -g {\ hat {r}}}$

onde g é a aceleração para baixo de 9,8 m / s ² devido à gravidade, e é um vetor unitário na direção radialmente para fora do centro do corpo gravitante. Portanto, aqui uma força adequada para fora de mg é necessária para evitar que a pessoa acelere para baixo. ${\ displaystyle {\ hat {r}}}$

Derivações de quatro vetores

As equações do espaço-tempo desta seção permitem abordar todos os desvios entre a aceleração adequada e coordenada em um único cálculo. Por exemplo, vamos calcular os símbolos de Christoffel :

${\ displaystyle \ left ({\ begin {array} {llll} \ left \ {\ Gamma _ {tt} ^ {t}, \ Gamma _ {tr} ^ {t}, \ Gamma _ {t \ theta} ^ {t}, \ Gamma _ {t \ phi} ^ {t} \ right \} & \ left \ {\ Gamma _ {rt} ^ {t}, \ Gamma _ {rr} ^ {t}, \ Gamma _ {r \ theta} ^ {t}, \ Gamma _ {r \ phi} ^ {t} \ right \} & \ left \ {\ Gamma _ {\ theta t} ^ {t}, \ Gamma _ {\ theta r} ^ {t}, \ Gamma _ {\ theta \ theta} ^ {t}, \ Gamma _ {\ theta \ phi} ^ {t} \ direita \} & \ esquerda \ {\ Gamma _ {\ phi t } ^ {t}, \ Gamma _ {\ phi r} ^ {t}, \ Gamma _ {\ phi \ theta} ^ {t}, \ Gamma _ {\ phi \ phi} ^ {t} \ right \} \\\ left \ {\ Gamma _ {tt} ^ {r}, \ Gamma _ {tr} ^ {r}, \ Gamma _ {t \ theta} ^ {r}, \ Gamma _ {t \ phi} ^ {r} \ right \} & \ left \ {\ Gamma _ {rt} ^ {r}, \ Gamma _ {rr} ^ {r}, \ Gamma _ {r \ theta} ^ {r}, \ Gamma _ {r \ phi} ^ {r} \ right \} & \ left \ {\ Gamma _ {\ theta t} ^ {r}, \ Gamma _ {\ theta r} ^ {r}, \ Gamma _ {\ theta \ theta} ^ {r}, \ Gamma _ {\ theta \ phi} ^ {r} \ right \} & \ left \ {\ Gamma _ {\ phi t} ^ {r}, \ Gamma _ {\ phi r } ^ {r}, \ Gamma _ {\ phi \ theta} ^ {r}, \ Gamma _ {\ phi \ phi} ^ {r} \ direita \} \\\ esquerda \ {\ Gamma _ {tt} ^ {\ theta}, \ Gamma _ {tr} ^ {\ theta}, \ Gamma _ {t \ theta} ^ {\ theta}, \ Gamma _ {t \ phi} ^ {\ theta} \ right \} & \ esquerda \ {\ Gamma _ { rt} ^ {\ theta}, \ Gamma _ {rr} ^ {\ theta}, \ Gamma _ {r \ theta} ^ {\ theta}, \ Gamma _ {r \ phi} ^ {\ theta} \ right \ } & \ left \ {\ Gamma _ {\ theta t} ^ {\ theta}, \ Gamma _ {\ theta r} ^ {\ theta}, \ Gamma _ {\ theta \ theta} ^ {\ theta}, \ Gamma _ {\ theta \ phi} ^ {\ theta} \ right \} & \ left \ {\ Gamma _ {\ phi t} ^ {\ theta}, \ Gamma _ {\ phi r} ^ {\ theta}, \ Gamma _ {\ phi \ theta} ^ {\ theta}, \ Gamma _ {\ phi \ phi} ^ {\ theta} \ direita \} \\\ esquerda \ {\ Gamma _ {tt} ^ {\ phi} , \ Gamma _ {tr} ^ {\ phi}, \ Gamma _ {t \ theta} ^ {\ phi}, \ Gamma _ {t \ phi} ^ {\ phi} \ direita \} & \ esquerda \ {\ Gamma _ {rt} ^ {\ phi}, \ Gamma _ {rr} ^ {\ phi}, \ Gamma _ {r \ theta} ^ {\ phi}, \ Gamma _ {r \ phi} ^ {\ phi} \ right \} & \ left \ {\ Gamma _ {\ theta t} ^ {\ phi}, \ Gamma _ {\ theta r} ^ {\ phi}, \ Gamma _ {\ theta \ theta} ^ {\ phi }, \ Gamma _ {\ theta \ phi} ^ {\ phi} \ right \} & \ left \ {\ Gamma _ {\ phi t} ^ {\ phi}, \ Gamma _ {\ phi r} ^ {\ phi}, \ Gamma _ {\ phi \ theta} ^ {\ phi}, \ Gamma _ {\ phi \ phi} ^ {\ phi} \ right \} \ end {array}} \ right)}$

para a métrica de Schwarzschild de coordenada distante ( c d τ ) ² = (1− r _s / r ) ( c d t ) ² - (1 / (1− r _s / r )) d r ² - r ² d θ ² - ( r sin  θ ) ² d φ ² , onde r _s é o raio de Schwarzschild 2 GM / c ² . A matriz resultante de coeficientes torna-se:

${\ displaystyle \ left ({\ begin {array} {llll} \ left \ {0, {\ frac {r_ {s}} {2r (r-r_ {s})}}, 0,0 \ right \} & \ left \ {{\ frac {r_ {s}} {2r (r-r_ {s})}}, 0,0,0 \ right \} & \ {0,0,0,0 \} & \ {0,0,0,0 \} \\\ left \ {{\ frac {r_ {s} c ^ {2} (r-r_ {s})} {2r ^ {3}}}, 0,0 , 0 \ direita \} & \ esquerda \ {0, {\ frac {r_ {s}} {2r (r_ {s} -r)}}, 0,0 \ direita \} & \ {0,0, r_ {s} -r, 0 \} & \ left \ {0,0,0, (r_ {s} -r) \ sin ^ {2} \ theta \ right \} \\\ {0,0,0, 0 \} & \ left \ {0,0, {\ frac {1} {r}}, 0 \ right \} & \ left \ {0, {\ frac {1} {r}}, 0,0 \ direita \} & \ {0,0,0, - \ cos \ theta \ sin \ theta \} \\\ {0,0,0,0 \} & \ left \ {0,0,0, {\ frac {1} {r}} \ right \} & \ {0,0,0, \ cot (\ theta) \} & \ left \ {0, {\ frac {1} {r}}, \ cot \ theta , 0 \ right \} \ end {array}} \ right)}$.

A partir disso, você pode obter a aceleração adequada da estrutura definindo a aceleração das coordenadas para zero e, portanto, exigindo que a aceleração adequada cancele a aceleração geométrica de um objeto estacionário, isto é . Isso ainda não resolve o problema, uma vez que as coordenadas de Schwarzschild no espaço-tempo curvo são coordenadas do guarda-livros, mas não as de um observador local. A magnitude do vetor 4 de aceleração adequada acima, a saber , é, no entanto, precisamente o que queremos, ou seja, a aceleração adequada invariante do quadro para cima necessária para neutralizar a aceleração geométrica para baixo sentida pelos habitantes da superfície de um planeta. ${\ displaystyle A ^ {\ lambda} = \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu} = \ {0, GM / r ^ {2} , 0,0 \}}$${\ displaystyle \ alpha = {\ sqrt {1 / (1-r_ {s} / r)}} GM / r ^ {2}}$

Um caso especial do conjunto de símbolos de Christoffel acima é o conjunto de coordenadas esféricas de espaço plano obtido definindo r _s ou M acima para zero:

${\ displaystyle \ left ({\ begin {array} {llll} \ left \ {0,0,0,0 \ right \} & \ left \ {0,0,0,0 \ right \} & \ {0 , 0,0,0 \} & \ {0,0,0,0 \} \\\ esquerda \ {0,0,0,0 \ direita \} & \ esquerda \ {0,0,0,0 \ direita \} & \ {0,0, -r, 0 \} & \ esquerda \ {0,0,0, -r \ sin ^ {2} \ theta \ direita \} \\\ {0,0,0 , 0 \} & \ left \ {0,0, {\ frac {1} {r}}, 0 \ right \} & \ left \ {0, {\ frac {1} {r}}, 0,0 \ right \} & \ {0,0,0, - \ cos \ theta \ sin \ theta \} \\\ {0,0,0,0 \} & \ left \ {0,0,0, {\ frac {1} {r}} \ right \} & \ {0,0,0, \ cot \ theta \} & \ left \ {0, {\ frac {1} {r}}, \ cot \ theta, 0 \ right \} \ end {array}} \ right)}$.

A partir disto, pode obter, por exemplo, o centri pétala aceleração adequada necessária para cancelar o centri em forma de fuga aceleração geométrica de um objecto em movimento a uma velocidade angular constante ω = d φ / d τ no equador onde θ = π / 2. Formar a mesma soma de 4 vetores como acima para o caso de d θ / d τ e d r / d τ zero resulta em nada mais do que a aceleração clássica para movimento rotacional dada acima, ou seja, de modo que a _o = ω ² r . Os efeitos de Coriolis também residem nesses coeficientes de conexão e surgem da mesma forma da geometria do quadro de coordenadas sozinho. ${\ displaystyle A ^ {\ lambda} = \ Gamma ^ {\ lambda} {} _ {\ mu \ nu} U ^ {\ mu} U ^ {\ nu} = \ {0, -r (d \ phi / d \ tau) ^ {2}, 0,0 \}}$

Veja também

• Aceleração : mudança na velocidade
• Velocidade adequada : momento por massa na relatividade especial; composto pelos componentes espaciais da velocidade de 4
• Quadro de referência adequado (espaço-tempo plano) : quadro de referência acelerado na relatividade especial (espaço de Minkowski)
• Força fictícia : um nome para massa vezes aceleração geométrica
• Quatro vetores : tornando explícita a conexão entre o espaço e o tempo
• Cinemática : para estudar as formas como a posição muda com o tempo
• Aceleração uniforme : mantendo a aceleração coordenada fixa

Notas de rodapé

links externos

• Trechos da primeira edição de Spacetime Physics e outros recursos postados por Edwin F. Taylor
• Página do livro de gravidade de James Hartle incluindo programas Mathematica para calcular símbolos de Christoffel.
• Notas e programas de Andrew Hamilton para trabalhar com tétrades locais em U. Colorado, Boulder.