Fórmula proposicional - Propositional formula
Na lógica proposicional , uma fórmula proposicional é um tipo de sintática fórmula que é bem formado e tem um valor de verdade . Se os valores de todas as variáveis em uma fórmula proposicional são dados, ela determina um valor verdade único. Uma fórmula proposicional também pode ser chamada de expressão proposicional , sentença ou fórmula sentencial .
Uma fórmula proposicional é construído a partir de simples proposições , tais como "cinco é maior do que três" ou variáveis proposicional , tais como p e q , usando conectivos ou operadores lógicos , tais como NÃO, E, OU, ou IMPLICA; por exemplo:
- ( p E NÃO q ) IMPLICA ( p OU q ).
Na matemática , uma fórmula proposicional é muitas vezes referida mais brevemente como uma " proposição ", mas, mais precisamente, uma fórmula proposicional não é uma proposição, mas uma expressão formal que denota uma proposição , um objeto formal em discussão, assim como uma expressão tal como " x + y " não é um valor, mas denota um valor. Em alguns contextos, manter a distinção pode ser importante.
Proposições
Para os fins do cálculo proposicional, as proposições (enunciados, sentenças, asserções) são consideradas simples ou compostas . As proposições compostas são consideradas ligadas por conectivos sentenciais , alguns dos mais comuns dos quais são "E", "OU", "SE ... ENTÃO ...", "NEM ... NEM ...", " ... É EQUIVALENTE A ..." . O ponto-e-vírgula de ligação ";" e o conectivo "MAS" são considerados expressões de "E". Uma sequência de sentenças discretas é considerada ligada por "AND" s, e a análise formal aplica uma "regra de parênteses" recursiva com respeito a sequências de proposições simples (veja mais abaixo sobre fórmulas bem formadas).
- Por exemplo: A afirmação: "Esta vaca é azul. Aquele cavalo é laranja, mas este cavalo aqui é roxo." é na verdade uma proposição composta ligada por "E" s: (("Esta vaca é azul" E "aquele cavalo é laranja") E "este cavalo aqui é roxo").
As proposições simples são declarativas por natureza, isto é, fazem afirmações sobre a condição ou natureza de um objeto particular de sensação, por exemplo, "Esta vaca é azul", "Há um coiote!" ("Aquele coiote ESTÁ lá , atrás das rochas."). Assim, as simples afirmações "primitivas" devem ser sobre objetos específicos ou estados de espírito específicos. Cada um deve ter pelo menos um sujeito (um objeto imediato de pensamento ou observação), um verbo (na voz ativa e no presente preferencial) e talvez um adjetivo ou advérbio. "Cão!" provavelmente implica "Vejo um cachorro", mas deve ser rejeitado por ser muito ambíguo.
- Exemplo: "Aquele cachorro roxo está correndo", "Esta vaca é azul", "Interruptor M31 está fechado", "Este boné está desligado", "Amanhã é sexta-feira".
Para os propósitos do cálculo proposicional, uma proposição composta pode geralmente ser reformulada em uma série de sentenças simples, embora o resultado provavelmente pareça artificial.
Relação entre fórmulas proposicionais e predicadas
O cálculo de predicados vai um passo além do cálculo proposicional para uma "análise da estrutura interna das proposições". Ele divide uma frase simples em duas partes (i) seu sujeito (o objeto ( singular ou plural) do discurso) e (ii ) um predicado (um verbo ou possivelmente verbo-cláusula que afirma uma qualidade ou atributo do (s) objeto (s)). O cálculo de predicado então generaliza a forma "sujeito | predicado" (onde | simboliza a concatenação ( encadeamento ) de símbolos) em uma forma com a seguinte estrutura de sujeito em branco "___ | predicado", e o predicado, por sua vez, generalizado para todas as coisas com essa propriedade.
- Exemplo: "Este porco azul tem asas" torna-se duas frases no cálculo proposicional : "Este porco tem asas" E "Este porco é azul", cuja estrutura interna não é considerada. Em contraste, no cálculo de predicados, a primeira frase se transforma em "este porco" como sujeito e "tem asas" como predicado. Assim, afirma que o objeto "este porco" é um membro da classe (conjunto, coleção) das "coisas aladas". A segunda frase afirma que o objeto "este porco" possui um atributo "azul" e, portanto, é um membro da classe das "coisas azuis". Pode-se escolher escrever as duas sentenças conectadas com AND como:
- p | W AND p | B
A generalização de "este porco" para um membro (potencial) de duas classes "coisas aladas" e "coisas azuis" significa que ele tem uma relação de verdade com ambas as classes. Em outras palavras, dado um domínio do discurso "coisas aladas", p é ou não um membro desse domínio. Assim, há uma relação W (alado) entre p (porco) e {T, F}, W (p) avalia para {T, F} onde {T, F} é o conjunto dos valores booleanos "verdadeiro" e " falso". Da mesma forma para B (azul) e p (porco) e {T, F}: B (p) avalia para {T, F}. Portanto, agora pode-se analisar as afirmações conectadas "B (p) AND W (p)" por seu valor de verdade geral, ou seja:
- (B (p) AND W (p)) avalia para {T, F}
Em particular, sentenças simples que empregam noções de "todos", "alguns", "alguns", "um de", etc., chamadas de quantificadores lógicos, são tratadas pelo cálculo de predicados. Junto com o novo simbolismo de função "F (x)", dois novos símbolos são introduzidos: ∀ (para todos) e ∃ (existe ..., pelo menos um de ... existe, etc.). O cálculo de predicados, mas não o cálculo proposicional, pode estabelecer a validade formal da seguinte afirmação:
- "Todos os porcos azuis têm asas, mas alguns porcos não têm asas, por isso alguns porcos não são azuis".
Identidade
Tarski afirma que a noção de IDENTIDADE (como distinta da EQUIVALÊNCIA LÓGICA) está fora do cálculo proposicional; no entanto, ele observa que se uma lógica deve ser útil para a matemática e as ciências, ela deve conter uma "teoria" de IDENTIDADE. Alguns autores referem-se a "lógica de predicado com identidade" para enfatizar essa extensão. Veja mais sobre isso abaixo.
Uma álgebra de proposições, o cálculo proposicional
Uma álgebra (e há muitos outros diferentes), vagamente definida, é um método pelo qual uma coleção de símbolos chamados variáveis junto com alguns outros símbolos como parênteses (,) e alguns subconjuntos de símbolos como *, +, ~ , &, ∨, =, ≡, ∧, ¬ são manipulados dentro de um sistema de regras. Diz-se que esses símbolos, e cadeias bem formadas deles, representam objetos , mas em um sistema algébrico específico esses objetos não têm significados . Assim, o trabalho dentro da álgebra torna-se um exercício de obediência a certas leis ( regras ) da sintaxe da álgebra (formação de símbolos), em vez de na semântica (significado) dos símbolos. Os significados devem ser encontrados fora da álgebra.
Para que uma sequência de símbolos bem formada na álgebra - uma fórmula - tenha alguma utilidade fora da álgebra, os símbolos recebem significados e, eventualmente, são atribuídos valores às variáveis ; então, por uma série de regras, a fórmula é avaliada .
Quando os valores são restritos a apenas dois e aplicados à noção de frases simples (por exemplo, declarações faladas ou asserções escritas) ligadas por conectivos proposicionais, todo este sistema algébrico de símbolos e regras e métodos de avaliação é geralmente chamado de cálculo proposicional ou cálculo sentencial .
Enquanto algumas das regras familiares da álgebra aritmética continuam a valer na álgebra de proposições (por exemplo, as leis comutativas e associativas para AND e OR), outras não (por exemplo, as leis distributivas para AND, OR e NOT).
Utilidade de fórmulas proposicionais
Análise : No raciocínio dedutivo , filósofos, retóricos e matemáticos reduzem os argumentos a fórmulas e então os estudam (geralmente com tabelas de verdade ) para correção (solidez). Por exemplo: O seguinte argumento é válido?
- "Dado que a consciência é suficiente para uma inteligência artificial e apenas entidades conscientes podem passar no teste de Turing , antes que possamos concluir que um robô é uma inteligência artificial, o robô deve passar no teste de Turing."
Os engenheiros analisam os circuitos lógicos que projetaram usando técnicas de síntese e, em seguida, aplicam várias técnicas de redução e minimização para simplificar seus projetos.
Síntese : os engenheiros, em particular, sintetizam fórmulas proposicionais (que eventualmente terminam como circuitos de símbolos) a partir de tabelas de verdade . Por exemplo, pode-se escrever uma tabela verdade de como a adição binária deve se comportar dada a adição das variáveis "b" e "a" e "carry_in" "ci", e os resultados "carry_out" "co" e "sum" Σ :
- Exemplo: na linha 5, ((b + a) + ci) = ((1 + 0) + 1) = o número "2". escrito como um número binário, é 10 2 , onde "co" = 1 e Σ = 0 conforme mostrado nas colunas mais à direita.
| fileira | b | uma | ci | (b + a) + ci | co | Σ | |
|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | |
| 2 | 0 | 1 | 0 | 1 | 0 | 1 | |
| 3 | 0 | 1 | 1 | 2 | 1 | 0 | |
| 4 | 1 | 0 | 0 | 1 | 0 | 1 | |
| 5 | 1 | 0 | 1 | 2 | 1 | 0 | |
| 6 | 1 | 1 | 0 | 2 | 1 | 0 | |
| 7 | 1 | 1 | 1 | 3 | 1 | 1 |
Variáveis proposicionais
O tipo mais simples de fórmula proposicional é uma variável proposicional . Proposições que são simples ( atômicas ), expressões simbólicas são frequentemente denotadas por variáveis chamadas p , q , ou P , Q , etc. Uma variável proposicional se destina a representar uma proposição atômica (asserção), como "É sábado" = p (aqui o símbolo = significa "... é atribuída a variável chamada ...") ou "Só vou ao cinema na segunda-feira" = q .
Atribuições de valores verdadeiros, avaliações de fórmulas
A avaliação de uma fórmula proposicional começa com a atribuição de um valor verdade a cada variável. Como cada variável representa uma frase simples, os valores verdadeiros estão sendo aplicados à "verdade" ou "falsidade" dessas frases simples.
Valores verdadeiros em retórica, filosofia e matemática : Os valores verdadeiros são apenas dois: {VERDADE "T", FALSIDADE "F"}. Um empirista coloca todas as proposições em duas classes amplas: analítica - verdadeira não importa o quê (por exemplo, tautologia ) e sintética - derivada da experiência e, portanto, suscetível de confirmação por terceiros (a teoria da verificação do significado). Os empíricos sustentam que, em geral, para chegar ao valor de verdade de uma proposição sintética , os significados (modelos de correspondência de padrões) devem primeiro ser aplicados às palavras, e então esses modelos de significado devem ser comparados com o que quer que esteja sendo afirmou. Por exemplo, minha declaração "Aquela vaca é azul !" Esta afirmação é uma VERDADE? Verdadeiramente eu disse isso. E talvez eu esteja vendo uma vaca azul - a menos que esteja mentindo, minha afirmação é uma VERDADE relativa ao objeto de minha (talvez falha) percepção. Mas a vaca azul está "realmente lá"? O que você vê quando olha pela mesma janela? Para prosseguir com a verificação, você precisará de uma noção prévia (um modelo) de "vaca" e " azul ", e uma capacidade de comparar os modelos com o objeto de sensação (se de fato houver um).
Valores verdadeiros em engenharia : os engenheiros tentam evitar noções de verdade e falsidade que atormentam os filósofos, mas, na análise final, os engenheiros devem confiar em seus instrumentos de medição. Em sua busca por robustez , os engenheiros preferem extrair objetos conhecidos de uma pequena biblioteca - objetos que têm comportamentos previsíveis e bem definidos, mesmo em grandes combinações (daí seu nome para o cálculo proposicional: "lógica combinatória"). Os menores comportamentos de um único objeto são dois (por exemplo, {OFF, ON}, {open, shut}, {UP, DOWN} etc.), e estes são colocados em correspondência com {0, 1}. Esses elementos são chamados de digitais ; aqueles com uma gama contínua de comportamentos são chamados de analógicos . Sempre que as decisões devem ser feitas em um sistema analógico, muitas vezes um engenheiro irá converter um comportamento analógico (a porta é 45,32146% PARA CIMA) para digital (por exemplo, BAIXO = 0) usando um comparador .
Assim, uma atribuição de significado das variáveis e dos dois símbolos de valor {0, 1} vem "de fora" da fórmula que representa o comportamento do objeto (geralmente) composto. Um exemplo é uma porta de garagem com dois "interruptores de limite", um para UP rotulado como SW_U e um para DOWN rotulado como SW_D, e tudo o mais que estiver no circuito da porta. A inspeção do circuito (o diagrama ou os próprios objetos reais - porta, interruptores, fios, placa de circuito, etc.) pode revelar que, na placa de circuito "nó 22" vai para +0 volts quando os contatos do interruptor "SW_D "estão mecanicamente em contato (" fechado ") e a porta está na posição" para baixo "(95% para baixo), e" nó 29 "vai para +0 volts quando a porta está 95% PARA CIMA e os contatos da chave SW_U estão em contato mecânico ("fechado"). O engenheiro deve definir os significados dessas tensões e todas as combinações possíveis (todas as 4), incluindo as "ruins" (por exemplo, ambos os nós 22 e 29 a 0 volts, o que significa que a porta está aberta e fechada ao mesmo tempo) . O circuito responde sem pensar a quaisquer tensões que ele experimenta, sem qualquer consciência da VERDADE ou FALSA, CERTO ou ERRADO, SEGURO ou PERIGOSO.
Conectivos proposicionais
Fórmulas proposicionais arbitrárias são construídas a partir de variáveis proposicionais e outras fórmulas proposicionais usando conectivos proposicionais . Exemplos de conectivos incluem:
- A negação unária conectiva. Se é uma fórmula, então é uma fórmula.
- Os conectivos binários clássicos . Assim, por exemplo, se e são fórmulas, então são .
- Outros conectivos binários, como NAND, NOR e XOR
- O conectivo ternário SE ... ENTÃO ... OUTRO ...
- Conetivos 0-ários constantes ⊤ e ⊥ (alternadamente, constantes {T, F}, {1, 0} etc.)
- O conectivo "teoria-extensão" É IGUAL (alternativamente, IDENTIDADE, ou o sinal "=" distinto do "conectivo lógico" )
Conectores de retórica, filosofia e matemática
A seguir estão os conectivos comuns à retórica, filosofia e matemática, juntamente com suas tabelas de verdade . Os símbolos usados variam de autor para autor e entre os campos de atuação. Em geral, as abreviações "T" e "F" representam as avaliações VERDADE e FALSIDADE aplicadas às variáveis na fórmula proposicional (por exemplo, a afirmação: "Essa vaca é azul" terá o valor de verdade "T" para Verdade ou " F "para Falsidade, conforme o caso.).
Os conectivos seguem vários usos de palavras diferentes, por exemplo, "a IMPLICA b" também é dito "SE a ENTÃO b". Alguns deles são mostrados na tabela.
| b apenas se um | |||||||||||
| b É SUFICIENTE PARA a | b PRECISAMENTE QUANDO a | ||||||||||
| a É NECESSÁRIO PARA b | b SE E SOMENTE SE a; b IFF a | ||||||||||
| inclusivo OU | SE b ENTÃO a | b É NECESSÁRIO E SUFICIENTE PARA a | |||||||||
| negação | negação | conjunção | disjunção | implicação | bicondicional | ||||||
| variáveis | Não ser | NÃO um | b AND a | b OU a | b IMPLICA a | b É logicamente equivalente a a *** | f É uma tautologia | NEM a NOR b | b traço a | exclusivo ou | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| b | uma | ¬ (b) | ¬ (a) | (b ∧ a) | (b ∨ a) | (b → a) | (b ↔ a) | (f = fórmula) | (a NOR b) | (b | a) | vários |
| F | F | T | T | F | F | T | T | T | T | T | F |
| F | T | T | F | F | T | T | F | T | F | T | T |
| T | F | F | T | F | T | F | F | T | F | T | T |
| T | T | F | F | T | T | T | T | T | F | F | F |
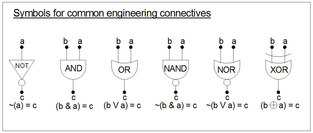
Conectivos de engenharia
Em geral, os conectivos de engenharia são exatamente os mesmos que os conectivos matemáticos, exceto que eles tendem a ser avaliados com "1" = "T" e "0" = "F". Isso é feito para fins de análise / minimização e síntese de fórmulas pelo uso da noção de mintermos e mapas de Karnaugh (ver abaixo). Os engenheiros também usam as palavras produto lógico da noção de Boole (a * a = a) e soma lógica da noção de Jevons (a + a = a).
| produto lógico | soma lógica | meio somador (sem transporte) | |||||||
|---|---|---|---|---|---|---|---|---|---|
| exclusivo ou | |||||||||
| número da linha | variáveis | NÃO | NÃO | E | OU | NAND | NEM | XOR | |
| b * 2 1 + a * 2 0 | b | uma | ~ (b) | ~ (a) | (BA) | (b ∨ a) | ~ (b & a) | ~ (b ∨ a) | ⊕ |
| 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 |
| 1 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 1 |
| 2 | 1 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 |
| 3 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 |
CONECTIVO CASE: SE ... ENTÃO ... OUTRO ...
O conectivo IF ... THEN ... ELSE ... aparece como a forma mais simples do operador CASE da teoria da recursão e da teoria da computação e é o conectivo responsável pelos goto's condicionais (saltos, ramos). A partir deste conector, todos os outros conectivos podem ser construídos (veja mais abaixo). Embora "IF c THEN b ELSE a" soe como uma implicação, é, em sua forma mais reduzida, uma troca que toma uma decisão e oferece como resultado apenas uma das duas alternativas "a" ou "b" (daí a declaração de troca de nome na linguagem de programação C ).
As três proposições a seguir são equivalentes (conforme indicado pelo sinal de equivalência lógica ≡):
- (SE 'o contador for zero' ENTÃO 'vá para a instrução b ' ELSE 'vá para a instrução a ') ≡
- ((c → b) & (~ c → a)) ≡ ((SE 'contador é zero' ENTÃO 'vá para a instrução b ') E (SE 'NÃO é o caso em que o contador é zero' ENTÃO 'vá para a instrução a ) "≡
- ((c & b) ∨ (~ c & a)) ≡ "('Contador é zero' E 'vá para a instrução b ) OU (' NÃO é o caso que 'contador é zero' E 'vá para a instrução a ) "
Assim, IF ... THEN ... ELSE - ao contrário da implicação - não avalia uma "VERDADE" ambígua quando a primeira proposição é falsa, isto é, c = F em (c → b). Por exemplo, a maioria das pessoas rejeitaria a seguinte proposição composta como um non sequitur sem sentido porque a segunda sentença não está conectada em significado à primeira.
- Exemplo: A proposição "SE 'Winston Churchill era chinês' ENTÃO 'o sol nasce no leste'" é avaliada como uma VERDADE, dado que 'Winston Churchill era chinês' é um FALSO e 'O sol nasce no leste' é avaliada como uma VERDADE .
Em reconhecimento desse problema, o sinal → da implicação formal no cálculo proposicional é chamado de implicação material para distingui-lo da implicação intuitiva cotidiana.
O uso da construção IF ... THEN ... ELSE evita controvérsias porque oferece uma escolha completamente determinística entre duas alternativas declaradas; oferece dois "objetos" (as duas alternativas b e a) e seleciona entre eles de forma exaustiva e inequívoca. Na tabela verdade abaixo, d1 é a fórmula: ((SE c ENTÃO b) E (SE NÃO-c ENTÃO a)). Sua forma totalmente reduzida d2 é a fórmula: ((c AND b) OR (NOT-c AND a). As duas fórmulas são equivalentes, conforme mostrado pelas colunas "= d1" e "= d2". Os engenheiros elétricos chamam o totalmente reduzido formula o operador AND-OR-SELECT. O operador CASE (ou SWITCH) é uma extensão da mesma ideia para n resultados possíveis, mas mutuamente exclusivos. Os engenheiros elétricos chamam o operador CASE de multiplexador .
| d1 | d2 | ||||||||||||||||||||||||||||||||||||||
| fileira | c | b | uma | ( | ( | c | → | b | ) | E | ( | ~ | ( | c | ) | → | uma | ) | ) | = d1 | ( | ( | c | E | b | ) | ∨ | ( | ~ | ( | c | ) | E | uma | ) | ) | = d2 | ||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 1 | 0 | 0 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 2 | 0 | 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | ||||||||||||||||||
| 3 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | ||||||||||||||||||
| 4 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | ||||||||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 0 | ||||||||||||||||||
| 6 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 | ||||||||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 |
IDENTIDADE e avaliação
A primeira tabela desta seção apresenta *** a entrada equivalência lógica para observar o fato de que " equivalência lógica " não é a mesma coisa que "identidade". Por exemplo, a maioria concordaria que a afirmação "Essa vaca é azul" é idêntica à afirmação "Essa vaca é azul". Por outro lado, a equivalência lógica às vezes aparece na fala como neste exemplo: "'O sol está brilhando' significa 'Estou pedalando'" Traduzida em uma fórmula proposicional, as palavras se tornam: "SE 'o sol está brilhando' ENTÃO ' Estou pedalando 'E SE' Estou pedalando 'ENTÃO' o sol está brilhando '":
- "SE 's' ENTÃO 'b' E SE 'b' ENTÃO 's'" é escrito como ((s → b) & (b → s)) ou em uma forma abreviada como (s ↔ b). Como a sequência de símbolos mais à direita é uma definição para um novo símbolo em termos dos símbolos à esquerda, o uso do sinal de IDENTIDADE = é apropriado:
- ((s → b) & (b → s)) = (s ↔ b)
Diferentes autores usam sinais diferentes para equivalência lógica: ↔ (por exemplo, Suppes, Goodstein, Hamilton), ≡ (por exemplo, Robbin), ⇔ (por exemplo, Bender e Williamson). Normalmente, a identidade é escrita como o sinal de igual =. Uma exceção a essa regra é encontrada em Principia Mathematica . Para mais informações sobre a filosofia da noção de IDENTIDADE, consulte a lei de Leibniz .
Como observado acima, Tarski considera que a IDENTIDADE está fora do cálculo proposicional, mas ele afirma que sem a noção, a "lógica" é insuficiente para a matemática e as ciências dedutivas. Na verdade, o sinal entra no cálculo proposicional quando uma fórmula deve ser avaliada.
Em alguns sistemas não há tabelas de verdade, mas apenas axiomas formais (por exemplo, cadeias de símbolos de um conjunto {~, →, (,), variáveis p 1 , p 2 , p 3 , ...} e regras de formação de fórmulas (regras sobre como fazer mais strings de símbolos a partir de strings anteriores usando, por exemplo, substituição e modus ponens ). o resultado de tal cálculo será outra fórmula (ou seja, uma string de símbolos bem formada). Eventualmente, no entanto, se alguém quiser Para usar o cálculo para estudar noções de validade e verdade, deve-se adicionar axiomas que definem o comportamento dos símbolos chamados "os valores verdade" {T, F} (ou {1, 0}, etc.) em relação aos outros símbolos.
Por exemplo, Hamilton usa dois símbolos = e ≠ quando ele define a noção de uma avaliação v de quaisquer fórmulas bem formadas (wffs) A e B em seu "cálculo de declaração formal" L. Uma avaliação v é uma função das wffs de seu sistema L ao intervalo (saída) {T, F}, dado que cada variável p 1 , p 2 , p 3 em uma wff é atribuída a um valor de verdade arbitrário {T, F}.
-
v ( A ) ≠ v (~ A )
( i )
-
v ( A → B ) = F se e somente se v ( A ) = T e v ( B ) = F
( ii )
As duas definições ( i ) e ( ii ) definem o equivalente das tabelas de verdade para os conectivos ~ (NOT) e → (IMPLICAÇÃO) de seu sistema. O primeiro deriva F ≠ T e T ≠ F, ou seja, " v ( A ) não significa v (~ A )". A definição ( ii ) especifica a terceira linha na tabela verdade, e as outras três linhas então vêm de uma aplicação da definição ( i ). Em particular ( ii ) atribui o valor F (ou um significado de "F") a toda a expressão. As definições também servem como regras de formação que permitem a substituição de um valor anteriormente derivado em uma fórmula:
| v (A → B) | ||||
| ( | v (A) | → | v (B) | ) |
| F | T | F | ||
| F | T | T | ||
| T | F | F | ||
| T | T | T |
Alguns sistemas formais especificam esses axiomas de avaliação desde o início na forma de certas fórmulas, como a lei da contradição ou as leis da identidade e da nulidade. A escolha de quais usar, juntamente com as leis como comutação e distribuição, cabe ao projetista do sistema, desde que o conjunto de axiomas seja completo (ou seja, suficiente para formar e avaliar qualquer fórmula bem formada criada no sistema) .
Fórmulas mais complexas
Conforme mostrado acima, o conectivo CASE (IF c THEN b ELSE a) é construído a partir dos conectivos de 2 argumentos IF ... THEN ... e AND ou de OR e AND e o argumento de 1 NOT. Conectores como o n-argumento AND (a & b & c & ... & n), OR (a ∨ b ∨ c ∨ ... ∨ n) são construídos a partir de strings de dois argumentos AND e OR e escritos em forma abreviada sem os parênteses. Esses e outros conectivos também podem ser usados como blocos de construção para outros conectivos. Retóricos, filósofos e matemáticos usam tabelas de verdade e os vários teoremas para analisar e simplificar suas fórmulas.
A engenharia elétrica usa símbolos desenhados e os conecta com linhas que representam o ato matemático de substituição e substituição . Eles então verificam seus desenhos com tabelas de verdade e simplificam as expressões como mostrado abaixo usando mapas de Karnaugh ou teoremas. Desta forma, os engenheiros criaram uma série de "lógica combinatória" (ou seja, conectivos sem feedback), como "decodificadores", "codificadores", "portas multifuncionais", "lógica majoritária", "somadores binários", "unidades lógicas aritméticas", etc.
Definições
Uma definição cria um novo símbolo e seu comportamento, geralmente para fins de abreviação. Uma vez que a definição é apresentada, qualquer forma do símbolo ou fórmula equivalente pode ser usada. O seguinte simbolismo = Df segue a convenção de Reichenbach. Alguns exemplos de definições convenientes extraídas do conjunto de símbolos {~, &, (,)} e variáveis. Cada definição está produzindo uma fórmula logicamente equivalente que pode ser usada para substituição ou substituição.
- definição de uma nova variável: (c & d) = Df s
- OU: ~ (~ a & ~ b) = Df (a ∨ b)
- IMPLICAÇÃO: (~ a ∨ b) = Df (a → b)
- XOR: (~ a & b) ∨ (a & ~ b) = Df (a ⊕ b)
- EQUIVALÊNCIA LÓGICA: ((a → b) & (b → a)) = Df (a ≡ b)
Esquemas de axioma e definição
As definições acima para OR, IMPLICAÇÃO, XOR e equivalência lógica são, na verdade, esquemas (ou "esquemas"), ou seja, são modelos (demonstrações, exemplos) para um formato de fórmula geral , mas mostrados (para fins ilustrativos) com letras específicas a , b, c para as variáveis, enquanto quaisquer letras de variáveis podem ir em seus lugares, desde que as substituições de letras sigam a regra de substituição abaixo.
- Exemplo: Na definição (~ a ∨ b) = Df (a → b), outros símbolos de variáveis como "SW2" e "CON1" podem ser usados, ou seja, formalmente:
- a = Df SW2, b = Df CON1, então teríamos como uma instância do esquema de definição (~ SW2 ∨ CON1) = Df (SW2 → CON1)
Substituição versus substituição
Substituição : A variável ou subfórmula a ser substituída por outra variável, constante ou subfórmula deve ser substituída em todas as instâncias ao longo da fórmula geral.
- Exemplo: (c & d) ∨ (p & ~ (c & ~ d)), mas (q1 e ~ q2) ≡ d. Agora, onde quer que a variável "d" ocorra, substitua (q 1 & ~ q 2 ):
- (c & (q 1 & ~ q 2 )) ∨ (p & ~ (c & ~ (q 1 & ~ q 2 )))
Substituição : (i) a fórmula a ser substituída deve estar dentro de uma tautologia, ou seja, logicamente equivalente (conectada por ≡ ou ↔) à fórmula que a substitui, e (ii) ao contrário da substituição, é permitido que a substituição ocorra apenas em um lugar (ou seja, para uma fórmula).
- Exemplo: use este conjunto de esquemas / equivalências de fórmulas:
- ((a ∨ 0) ≡ a).
- ((a & ~ a) ≡ 0).
- ((~ a ∨ b) = Df (a → b)).
- (~ (~ a) ≡ a)
- comece com "a": a
- Use 1 para substituir "a" por (a ∨ 0): (a ∨ 0)
- Use a noção de "esquema" para substituir b por a em 2: ((a & ~ a) ≡ 0)
- Use 2 para substituir 0 por (b & ~ b): (a ∨ (b & ~ b))
- (veja abaixo como distribuir "a ∨" em (b & ~ b), etc.)
Definição indutiva
A apresentação clássica da lógica proposicional (ver Enderton 2002) usa os conectivos . O conjunto de fórmulas sobre um determinado conjunto de variáveis proposicionais é indutivamente definido como o menor conjunto de expressões como:
- Cada variável proposicional no conjunto é uma fórmula,
- é uma fórmula sempre que for, e
- é uma fórmula sempre que e são fórmulas e é um dos conectivos binários .
Esta definição indutiva pode ser facilmente estendida para cobrir conectivos adicionais.
A definição indutiva também pode ser reformulada em termos de uma operação de fechamento (Enderton 2002). Deixe V denotar um conjunto de variáveis proposicionais e X V denotar o conjunto de todas as cadeias de caracteres de um alfabeto, incluindo símbolos em V , parênteses esquerdo e direito e todos os conectivos lógicos sob consideração. Cada conectivo lógico corresponde a uma operação de construção de fórmula, uma função de XX V a XX V :
- Dada uma string z , a operação retorna .
- Dadas as strings y e z , a operação retorna . Há operações similares , e correspondendo aos outros conectivos binários.
O conjunto de fórmulas sobre V é definido como o menor subconjunto de XX V contendo V e fechado em todas as operações de construção de fórmula.
Fórmulas de análise
As seguintes "leis" do cálculo proposicional são usadas para "reduzir" fórmulas complexas. As "leis" podem ser verificadas facilmente com tabelas de verdade. Para cada lei, o conectivo principal (mais externo) está associado à equivalência lógica ≡ ou identidade =. Uma análise completa de todas as 2 n combinações de valores de verdade para suas n variáveis distintas resultará em uma coluna de 1's (T's) abaixo desse conectivo. Esse achado torna cada lei, por definição, uma tautologia. E, para uma dada lei, porque suas fórmulas à esquerda e à direita são equivalentes (ou idênticas), elas podem ser substituídas uma pela outra.
- Exemplo: A seguinte tabela de verdade é a lei de De Morgan para o comportamento de NOT sobre OR: ~ (a ∨ b) ≡ (~ a & ~ b). À esquerda do conectivo principal ≡ (coluna amarela rotulada "esticada") a fórmula ~ (b ∨ a) é avaliada como (1, 0, 0, 0) sob o rótulo "P". À direita de "esticado", a fórmula (~ (b) ∨ ~ (a)) também avalia (1, 0, 0, 0) sob o rótulo "Q". Como as duas colunas têm avaliações equivalentes, a equivalência lógica ≡ em "tenso" é avaliada como (1, 1, 1, 1), ou seja, P ≡ Q. Assim, qualquer fórmula pode ser substituída pela outra se aparecer em uma fórmula maior.
| P | tenso | Q | ||||||||||||||||||||
| b | uma | ( | ~ | ( | b | V | uma | ) | ≡ | ( | ~ | ( | b | ) | E | ~ | ( | uma | ) | ) | ) | |
| 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 0 | |||||||||||
| 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 1 | 0 | 1 | 0 | 1 | 0 | |||||||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 0 | 1 |
Leitores empreendedores podem se desafiar a inventar um "sistema axiomático" que use os símbolos {∨, &, ~, (,), variáveis a, b, c}, as regras de formação especificadas acima e o mínimo possível das leis listadas abaixo, e então derive como teoremas os outros, bem como as avaliações da tabela de verdade para ∨, & e ~. Um conjunto atribuído a Huntington (1904) (Suppes: 204) usa oito das leis definidas abaixo.
Se usados em um sistema axiomático, os símbolos 1 e 0 (ou T e F) são considerados fórmulas bem formadas e, portanto, obedecem às mesmas regras das variáveis. Assim, as leis listadas abaixo são, na verdade , esquemas de axiomas , ou seja, substituem um número infinito de instâncias. Assim, (x ∨ y) ≡ (y ∨ x) pode ser usado em uma instância, (p ∨ 0) ≡ (0 ∨ p) e em outra instância (1 ∨ q) ≡ (q ∨ 1), etc.
Antiguidade conectiva (classificação do símbolo)
Em geral, para evitar confusão durante a análise e avaliação de fórmulas proposicionais, faça uso liberal de parênteses. No entanto, muitas vezes os autores os deixam de fora. Para analisar uma fórmula complicada, primeiro é necessário saber a antiguidade , ou classificação , que cada um dos conectivos (exceto *) tem sobre os outros conectivos. Para "formar bem" uma fórmula, comece com o conectivo com a classificação mais alta e adicione parênteses ao redor de seus componentes, depois vá para baixo na classificação (prestando muita atenção ao escopo do conectivo sobre o qual ele está trabalhando). Do mais ao menos sênior, com os sinais de predicado ∀x e ∃x, a IDENTIDADE = e os sinais aritméticos adicionados para completar:
- ≡
- (EQUIVALÊNCIA LÓGICA)
- →
- (IMPLICAÇÃO)
- E
- (E)
- ∨
- (OU)
- ~
- (NÃO)
- ∀x
- (PARA TODOS x)
- ∃x
- (EXISTE UM x)
- =
- (IDENTIDADE)
- +
- (soma aritmética)
- *
- (multiplicação aritmética)
- '
- (s, sucessor aritmético).
Assim, a fórmula pode ser analisada, mas porque NÃO não obedece à lei distributiva, os parênteses em torno da fórmula interna (~ c & ~ d) são obrigatórios:
- Exemplo: "d & c ∨ w" reescrito é ((d & c) ∨ w)
- Exemplo: "a & a → b ≡ a & ~ a ∨ b" reescrito (rigorosamente) é
- ≡ tem antiguidade: ((a & a → b) ≡ (a & ~ a ∨ b))
- → tem antiguidade: ((a & (a → b)) ≡ (a & ~ a ∨ b))
- & tem antiguidade em ambos os lados: ((((a) & (a → b))) ≡ (((a) & (~ a ∨ b)))
- ~ tem antiguidade: ((((a) & (a → b))) ≡ (((a) & (~ (a) ∨ b)))
- verifique 9 (-parêntese e 9) -parêntese: (((((a) & (a → b))) ≡ (((a) & (~ (a) ∨ b)))
- Exemplo:
- d & c ∨ p & ~ (c & ~ d) ≡ c & d ∨ p & c ∨ p & ~ d reescrito é (((d & c) ∨ (p & ~ ((c & ~ (d)))) )) ≡ ((c & d) ∨ (p & c) ∨ (p & ~ (d))))
Leis comutativas e associativas
Ambos AND e OR obedecem à lei comutativa e à lei associativa :
- Lei comutativa para OR: (a ∨ b) ≡ (b ∨ a)
- Lei comutativa para AND: (a & b) ≡ (b & a)
- Lei associativa para OR: ((a ∨ b) ∨ c) ≡ (a ∨ (b ∨ c))
- Lei associativa para AND: ((a & b) & c) ≡ (a & (b & c))
Omitindo parênteses em strings de AND e OR : Os conectivos são considerados unários (uma variável, por exemplo, NOT) e binários (ou seja, duas variáveis AND, OR, IMPLIES). Por exemplo:
- ((c & d) ∨ (p & c) ∨ (p & ~ d)) acima deve ser escrito (((c & d) ∨ (p & c)) ∨ (p & ~ (d))) ou possivelmente ((c & d) ∨ ((p & c) ∨ (p & ~ (d))))
No entanto, uma demonstração de tabela de verdade mostra que a forma sem os parênteses extras é perfeitamente adequada.
Omitindo parênteses com relação a uma única variável NOT : Enquanto ~ (a) onde a é uma única variável é perfeitamente claro, ~ a é adequado e é a maneira usual que este literal apareceria. Quando o NOT está sobre uma fórmula com mais de um símbolo, os parênteses são obrigatórios, por exemplo, ~ (a ∨ b).
Leis distributivas
OR distribui por AND e AND distribui por OR. NOT não distribui por AND ou OR. Veja abaixo sobre a lei De Morgan:
- Lei distributiva para OR: (c ∨ (a & b)) ≡ ((c ∨ a) & (c ∨ b))
- Lei distributiva para AND: (c & (a ∨ b)) ≡ ((c & a) ∨ (c & b))
Leis De Morgan
NÃO, quando distribuído por OR ou AND, faz algo peculiar (novamente, isso pode ser verificado com uma tabela de verdade):
- Lei de De Morgan para OR: ¬ (a ∨ b) ≡ (¬a ^ ¬b)
- Lei de De Morgan para AND: ¬ (a ^ b) ≡ (¬a ∨ ¬b)
Leis de absorção
A absorção, em particular a primeira, faz com que as "leis" da lógica sejam diferentes das "leis" da aritmética:
- Absorção (idempotência) para OR: (a ∨ a) ≡ a
- Absorção (idempotência) para AND: (a & a) ≡ a
Leis de avaliação: Identidade, nulidade e complemento
O sinal "=" (distinto da equivalência lógica ≡, alternadamente ↔ ou ⇔) simboliza a atribuição de valor ou significado. Assim, a string (a & ~ (a)) simboliza "0", ou seja, significa a mesma coisa que o símbolo "0" ". Em alguns" sistemas ", este será um axioma (definição), talvez mostrado como ((a & ~ (a)) = Df 0); em outros sistemas, pode ser derivado na tabela verdade abaixo:
| c | tenso | c | |||||||||||
| uma | ( | ( | uma | E | ~ | ( | uma | ) | ) | ≡ | 0 | ) | |
| 0 | 0 | 0 | 1 | 0 | 1 | 0 | |||||||
| 1 | 1 | 0 | 0 | 1 | 1 | 0 |
- Comutação de igualdade: (a = b) ≡ (b = a)
- Identidade para OR: (a ∨ 0) = a ou (a ∨ F) = a
- Identidade para AND: (a & 1) = a ou (a & T) = a
- Nulidade para OR: (a ∨ 1) = 1 ou (a ∨ T) = T
- Nulidade para AND: (a & 0) = 0 ou (a & F) = F
- Complemento para OR: (a ∨ ~ a) = 1 ou (a ∨ ~ a) = T, lei do meio excluído
- Complemento para AND: (a & ~ a) = 0 ou (a & ~ a) = F, lei da contradição
Duplo negativo (involução)
- ¬ (¬a) ≡ a
Fórmulas bem formadas (wffs)
Uma propriedade chave das fórmulas é que elas podem ser analisadas exclusivamente para determinar a estrutura da fórmula em termos de suas variáveis proposicionais e conectivos lógicos. Quando as fórmulas são escritas em notação infixa , como acima, a legibilidade única é garantida por meio do uso apropriado de parênteses na definição das fórmulas. Alternativamente, as fórmulas podem ser escritas em notação polonesa ou notação polonesa reversa , eliminando a necessidade de parênteses.
A definição indutiva de fórmulas infixas na seção anterior pode ser convertida em uma gramática formal na forma Backus-Naur :
<formula> ::= <propositional variable>
| ( ¬ <formula> )
| ( <formula> ∧ <formula>)
| ( <formula> ∨ <formula> )
| ( <formula> → <formula> )
| ( <formula> ↔ <formula> )
Pode-se mostrar que qualquer expressão correspondida pela gramática tem um número equilibrado de parênteses esquerdo e direito, e qualquer segmento inicial não vazio de uma fórmula tem mais parênteses esquerdo do que direito. Esse fato pode ser usado para fornecer um algoritmo para a análise de fórmulas. Por exemplo, suponha que uma expressão x comece com . Começando depois do segundo símbolo, combine a menor subexpressão y de x que possui parênteses equilibrados. Se x for uma fórmula, há exatamente um símbolo restante após essa expressão, esse símbolo é um parêntese de fechamento e o próprio y é uma fórmula. Essa ideia pode ser usada para gerar um analisador descendente recursivo para fórmulas.
Exemplo de contagem de parênteses :
Este método localiza como "1" o conectivo principal - o conectivo sob o qual a avaliação geral da fórmula ocorre para os parênteses mais externos (que são freqüentemente omitidos). Ele também localiza o conectivo mais interno, onde se iniciaria a avaliação da fórmula sem o uso de uma tabela verdade, por exemplo, no "nível 6".
| começar | ( | ( | ( | c | E | d | ) | V | ( | p | E | ~ | ( | ( | c | E | ~ | ( | d | ) | ) | ) | ) | ) | = | ( | ( | ( | c | E | d | ) | V | ( | p | E | d | ) | ) | V | ( | p | E | ~ | ( | c | ) | ) | ) | ) | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| contar | 0 | 1 | 2 | 3 | 3 | 3 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 4 | 5 | 5 | 5 | 5 | 6 | 6 | 5 | 4 | 3 | 3 | 1 | 1 | 2 | 3 | 4 | 4 | 4 | 4 | 3 | 3 | 4 | 4 | 4 | 4 | 3 | 2 | 2 | 3 | 3 | 3 | 3 | 3 | 3 | 3 | 2 | 1 | 0 |
Fórmulas bem formadas versus fórmulas válidas em inferências
A noção de argumento válido é geralmente aplicada a inferências em argumentos, mas os argumentos se reduzem a fórmulas proposicionais e podem ser avaliados da mesma forma que qualquer outra fórmula proposicional. Aqui, uma inferência válida significa: "A fórmula que representa a inferência é avaliada como" verdade "sob seu conectivo principal, não importa quais valores de verdade sejam atribuídos às suas variáveis", isto é, a fórmula é uma tautologia. Muito possivelmente, uma fórmula será bem formada, mas não válida . Outra maneira de dizer isso é: "Ser bem formado é necessário para que uma fórmula seja válida, mas não é suficiente ." A única maneira de descobrir se ele é tanto bem formado e válido é submetê-lo a uma verificação com uma mesa de verdade ou pelo uso das "leis":
- Exemplo 1: O que fazer com a seguinte afirmação difícil de seguir? É válido? "Se está ensolarado, mas se o sapo está coaxando, então não está ensolarado, então é o mesmo que dizer que o sapo não está coaxando." Converta isso em uma fórmula proposicional da seguinte maneira:
- "IF (a AND (IF b THEN NOT-a) THEN NOT-a" onde "a" representa "seu sol" e "b" representa "o sapo está coaxando":
- (((a) & ((b) → ~ (a)) ≡ ~ (b))
- Isso está bem formado, mas é válido ? Em outras palavras, quando avaliado, isso produzirá uma tautologia (todo T) abaixo do símbolo de equivalência lógica ≡? A resposta é NÃO, não é válido. No entanto, se reconstruído como uma implicação , o argumento é válido.
- "Dizer que está ensolarado, mas se o sapo está coaxando, então não está ensolarado, implica que o sapo não está coaxando."
- Outras circunstâncias podem estar impedindo o sapo de coaxar: talvez um guindaste o tenha comido.
- Exemplo 2 (de Reichenbach via Bertrand Russell):
- "Se os porcos têm asas, alguns animais alados são bons para comer. Alguns animais alados são bons para comer, então os porcos têm asas."
- (((a) → (b)) & (b) → (a)) é bem formado, mas um argumento inválido como mostrado pela avaliação em vermelho sob a implicação principal:
| C | G | arg | |||||||||||||
| uma | b | ( | ( | ( | uma | -> | b | ) | E | b | ) | -> | uma | ) | |
| 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||
| 0 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | |||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 1 | |||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
Conjuntos reduzidos de conectivos

Um conjunto de conectivos lógicos é denominado completo se cada fórmula proposicional for tautologicamente equivalente a uma fórmula apenas com os conectivos nesse conjunto. Há muitos conjuntos completos de conectivos, incluindo , e . Existem dois conectivos binários completos por conta própria, correspondendo a NAND e NOR, respectivamente. Alguns pares não estão completos, por exemplo .
O traço (NAND)
O conectivo binário correspondente a NAND é chamado de traço de Sheffer e é escrito com uma barra vertical | ou seta vertical ↑. A integridade desse conectivo foi observada em Principia Mathematica (1927: xvii). Uma vez que é completo por conta própria, todos os outros conectivos podem ser expressos usando apenas o traço. Por exemplo, onde o símbolo "≡" representa a equivalência lógica :
- ~ p ≡ p | p
- p → q ≡ p | ~ q
- p ∨ q ≡ ~ p | ~ q
- p & q ≡ ~ (p | q)
Em particular, os conectivos zero-ários (representando a verdade) e (representando a falsidade) podem ser expressos usando o traço:
SE ... ENTÃO ... OUTRO
Este conectivo junto com {0, 1}, (ou {F, T} ou { , }) forma um conjunto completo. No seguinte o IF ... THEN ... ELSE relação (c, b, a) = d representa ((c → b) ∨ (~ c → a)) ≡ ((C & b) ∨ (~ c & a)) = d
- (c, b, a):
- (c, 0, 1) ≡ ~ c
- (c, b, 1) ≡ (c → b)
- (c, c, a) ≡ (c ∨ a)
- (c, b, c) ≡ (c & b)
Exemplo: O seguinte mostra como uma prova baseada em teoremas de "(c, b, 1) ≡ (c → b)" continuaria, abaixo da prova está sua verificação da tabela de verdade. (Nota: (c → b) é definido como (~ c ∨ b)):
- Comece com a forma reduzida: ((c & b) ∨ (~ c & a))
- Substitua "1" por a: ((c & b) ∨ (~ c & 1))
- Identidade (~ c & 1) = ~ c: ((c & b) ∨ (~ c))
- Lei da comutação para V: ((~ c) ∨ (c & b))
- Distribua "~ c V" sobre (c & b): (((~ c) ∨ c) & ((~ c) ∨ b)
- Lei do meio excluído (((~ c) ∨ c) = 1): ((1) & ((~ c) ∨ b))
- Distribuir "(1) &" sobre ((~ c) ∨ b): (((1) & (~ c)) ∨ ((1) & b)))
- Comutividade e identidade ((1 & ~ c) = (~ c & 1) = ~ c, e ((1 & b) ≡ (b & 1) ≡ b: (~ c ∨ b)
- (~ c ∨ b) é definido como c → b QED
Na tabela de verdade a seguir, a coluna rotulada "tensa" para tautologia avalia a equivalência lógica (simbolizada aqui por ≡) entre as duas colunas rotuladas d. Como todas as quatro linhas sob "tenso" são 1's, a equivalência de fato representa uma tautologia.
| d | tenso | d | |||||||||||||||||||||||||||||
| filas | c | b | uma | ( | ( | ( | c | E | b | ) | V | ( | ~ | ( | c | ) | E | uma | ) | ) | ≡ | ( | ~ | ( | c | ) | V | b | ) | ) | |
| 0,1 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | |||||||||||||||
| 2,3 | 0 | 1 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | 1 | |||||||||||||||
| 4,5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 0 | 0 | |||||||||||||||
| 6,7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | 0 | 1 | 1 | 0 | 1 | 1 | 1 |
Formas normais
Uma fórmula proposicional arbitrária pode ter uma estrutura muito complicada. Freqüentemente, é conveniente trabalhar com fórmulas que possuem formas mais simples, conhecidas como formas normais . Algumas formas normais comuns incluem a forma normal conjuntiva e a forma normal disjuntiva . Qualquer fórmula proposicional pode ser reduzida à sua forma normal conjuntiva ou disjuntiva.
Redução à forma normal

A redução à forma normal é relativamente simples, uma vez que uma tabela verdade para a fórmula é preparada. Mas outras tentativas de minimizar o número de literais (veja abaixo) requerem algumas ferramentas: a redução pelas leis de De Morgan e tabelas de verdade pode ser difícil de manejar, mas os mapas de Karnaugh são muito adequados para um pequeno número de variáveis (5 ou menos). Existem alguns métodos tabulares sofisticados para circuitos mais complexos com várias saídas, mas estão além do escopo deste artigo; para obter mais informações, consulte o algoritmo Quine – McCluskey .
Literal, termo e alterm
Na engenharia elétrica, uma variável x ou sua negação ~ (x) é agrupada em uma única noção chamada literal . Uma string de literais conectadas por ANDs é chamada de termo . Uma string de literais conectadas por OR é chamada de alterm . Normalmente, o literal ~ (x) é abreviado como ~ x. Às vezes, o símbolo & é totalmente omitido na forma de multiplicação algébrica.
- Exemplos
- a, b, c, d são variáveis. (((a & ~ (b)) & ~ (c)) & d) é um termo. Isso pode ser abreviado como (a & ~ b & ~ c & d) ou a ~ b ~ cd.
- p, q, r, s são variáveis. (((p & ~ (q)) & r) & ~ (s)) é um alterm. Isso pode ser abreviado como (p ∨ ~ q ∨ r ∨ ~ s).
Minterms
Da mesma forma que uma tabela de verdade de 2 n linhas exibe a avaliação de uma fórmula proposicional para todos os 2 n valores possíveis de suas variáveis, n variáveis produzem um mapa de Karnaugh 2 n- quadrado (embora não possamos desenhá-lo em sua totalidade realização dimensional). Por exemplo, 3 variáveis produzem 2 3 = 8 linhas e 8 quadrados de Karnaugh; 4 variáveis produzem 16 linhas da tabela de verdade e 16 quadrados e, portanto, 16 mintermos . Cada quadrado do mapa de Karnaugh e sua avaliação da tabela de verdade correspondente representam um mintermo.
Qualquer fórmula proposicional pode ser reduzida à "soma lógica" (OR) dos mintermos ativos (isto é, "1" - ou "T" -valorizado). Quando nesta forma, a fórmula é considerada na forma normal disjuntiva . Mas, embora seja nesta forma, não é necessariamente minimizado com relação ao número de termos ou ao número de literais.
Na tabela a seguir, observe a numeração peculiar das linhas: (0, 1, 3, 2, 6, 7, 5, 4, 0). A primeira coluna é o equivalente decimal do equivalente binário dos dígitos "cba", ou seja:
- Exemplo
- cba 2 = c * 2 2 + b * 2 1 + a * 2 0 :
- cba = (c = 1, b = 0, a = 0) = 101 2 = 1 * 2 2 + 0 * 2 1 + 1 * 2 0 = 5 10
Essa numeração ocorre porque, à medida que se desce na tabela, de linha em linha, apenas uma variável de cada vez muda seu valor. O código cinza é derivado dessa noção. Essa noção pode ser estendida para hipercubos tridimensionais e quadridimensionais chamados diagramas de Hasse, onde as variáveis de cada canto mudam apenas uma de cada vez à medida que se move ao redor das bordas do cubo. Os diagramas de Hasse (hipercubos) achatados em duas dimensões são diagramas de Veitch ou mapas de Karnaugh (são virtualmente a mesma coisa).
Ao trabalhar com mapas de Karnaugh, deve-se sempre ter em mente que a borda superior "envolve" a borda inferior, e a borda esquerda envolve a borda direita - o diagrama de Karnaugh é realmente tridimensional ou quadridimensional objeto achatado.
| equivalente decimal de (c, b, a) | c | b | uma | mintermo |
|---|---|---|---|---|
| 0 | 0 | 0 | 0 | (~ c & ~ b & ~ a) |
| 1 | 0 | 0 | 1 | (~ c & ~ b & a) |
| 3 | 0 | 1 | 1 | (~ c & b & a) |
| 2 | 0 | 1 | 0 | (~ c & b & ~ a) |
| 6 | 1 | 1 | 0 | (c & b & ~ a) |
| 7 | 1 | 1 | 1 | (c & b & a) |
| 5 | 1 | 0 | 1 | (c & ~ b & a) |
| 4 | 1 | 0 | 0 | (c & ~ b & ~ a) |
| 0 | 0 | 0 | 0 | (~ a & ~ b & ~ c) |
Redução pelo uso do método de mapa (Veitch, Karnaugh)
Veitch melhorou a noção de diagramas de Venn convertendo os círculos em quadrados adjacentes, e Karnaugh simplificou o diagrama de Veitch convertendo os mintermos, escritos em sua forma literal (por exemplo, ~ abc ~ d) em números. O método procede da seguinte forma:
Produza a tabela de verdade da fórmula
Produza a tabela verdade da fórmula. Numere suas linhas usando os equivalentes binários das variáveis (geralmente apenas sequencialmente de 0 a n-1) para n variáveis.
- Tecnicamente, a função proposicional foi reduzida à sua forma normal conjuntiva (não minimizada): cada linha tem sua expressão de mintermo e estes podem ser OR para produzir a fórmula em sua forma normal conjuntiva (não minimizada).
Exemplo: ((c & d) ∨ (p & ~ (c & (~ d)))) = q na forma normal conjuntiva é:
- ((~ p & d & c) ∨ (p & d & c) ∨ (p & d & ~ c) ∨ (p & ~ d & ~ c)) = q
No entanto, essa fórmula pode ser reduzida tanto no número de termos (de 4 para 3) quanto na contagem total de seus literais (12 para 6).
| fileira | Minterms | p | d | c | ( | ( | c | E | d | ) | ∨ | ( | p | E | ~ | ( | ( | c | E | ~ | ( | d | ) | ) | ) | ) | ) | Mintermos ativos | Fórmula na forma normal conjuntiva |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (~ p & ~ d & ~ c) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | ||||||||||||||
| 1 | (~ p & ~ d & c) | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 2 | (~ p & d & ~ c) | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | ||||||||||||||
| 3 | (~ p & d & c) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | (~ p & d & c) | |||||||||||||
| 4 | (p & ~ d & ~ c) | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | (~ p & d & c) | |||||||||||||
| 5 | (p & ~ d & c) | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | ||||||||||||||
| 6 | (p & d & ~ c) | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | (p & d & ~ c) | |||||||||||||
| 7 | (p & d & c) | 1 | 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | (p & d & c) | |||||||||||||
| q | = (~ p & d & c) ∨ (~ p & d & c) ∨ (p & d & ~ c) ∨ (p & d & c) |
Crie o mapa de Karnaugh da fórmula
Use os valores da fórmula (por exemplo, "p") encontrados pelo método da tabela de verdade e coloque-os em seus respectivos quadrados de Karnaugh (associados) (eles são numerados de acordo com a convenção do código de Gray). Se valores de "d" para "irrelevante" aparecem na tabela, isso adiciona flexibilidade durante a fase de redução.
Reduzir mintermos
Mintermos de 1-quadrados adjacentes (adjacentes) (quadrados T) podem ser reduzidos em relação ao número de seus literais , e os termos numéricos também serão reduzidos no processo. Dois quadrados adjacentes (2 x 1 horizontal ou 1 x 2 vertical, até mesmo as bordas representam quadrados adjacentes) perdem um literal, quatro quadrados em um retângulo 4 x 1 (horizontal ou vertical) ou 2 x 2 quadrados (mesmo os quatro cantos representam adjacentes quadrados) perdem dois literais, oito quadrados em um retângulo perdem 3 literais, etc. (Busca-se o maior quadrado ou retângulos e ignora-se os quadrados menores ou retângulos contidos totalmente dentro dele.) Este processo continua até que todos os quadrados adjacentes sejam contabilizados, em qual ponto a fórmula proposicional é minimizada.
Por exemplo, os quadrados 3 e 7 ficam próximos. Esses dois quadrados adjacentes podem perder um literal (por exemplo, "p" dos quadrados # 3 e # 7), quatro quadrados em um retângulo ou quadrado perdem dois literais, oito quadrados em um retângulo perdem 3 literais, etc. (Um procura o maior (quadrados ou retângulos). Esse processo continua até que todos os quadrados adjacentes sejam contabilizados, ponto em que a fórmula proposicional é considerada minimizada.
Exemplo: O método do mapa geralmente é feito por inspeção. O exemplo a seguir expande o método algébrico para mostrar o "truque" por trás da combinação de termos em um mapa de Karnaugh:
- Os mintermos # 3 e # 7 confinam, # 7 e # 6 confinam, e # 4 e # 6 confinam (porque as bordas da mesa se enrolam). Portanto, cada um desses pares pode ser reduzido.
Observe que pela lei de idempotência (A ∨ A) = A, podemos criar mais termos. Então, por associação e leis distributivas, as variáveis a desaparecer podem ser emparelhadas e, em seguida, "desaparecer" com a Lei da contradição (x & ~ x) = 0. O seguinte usa colchetes [e] apenas para controlar os termos; eles não têm nenhum significado especial:
- Coloque a fórmula na forma normal conjuntiva com a fórmula a ser reduzida:
- q = ((~ p & d & c) ∨ (p & d & c) ∨ (p & d & ~ c) ∨ (p & ~ d & ~ c)) = (# 3 ∨ # 7 ∨ # 6 ∨ # 4)
- Idempotência (absorção) [A ∨ A) = A:
- (# 3 ∨ [# 7 ∨ # 7] ∨ [# 6 ∨ # 6] ∨ # 4)
- Lei associativa (x ∨ (y ∨ z)) = ((x ∨ y) ∨ z)
- ([# 3 ∨ # 7] ∨ [# 7 ∨ # 6] ∨ [# 6 ∨ # 4])
- [ (~ p & d & c) ∨ (p & d & c) ] ∨ [ (p & d & c) ∨ (p & d & ~ c) ] ∨ [ (p & d & ~ c) ∨ (p & ~ d & ~ c) ] .
- Lei distributiva (x & (y ∨ z)) = ((x & y) ∨ (x & z)):
- ([(d & c) ∨ (~ p & p)] ∨ [(p & d) ∨ (~ c & c)] ∨ [(p & ~ c) ∨ (c & ~ c)])
- Lei comutativa e lei da contradição (x & ~ x) = (~ x & x) = 0:
- ([(d & c) ∨ (0)] ∨ [(p & d) ∨ (0)] ∨ [(p & ~ c) ∨ (0)])
- Lei da identidade (x ∨ 0) = x levando à forma reduzida da fórmula:
- q = ((d & c) ∨ (p & d) ∨ (p & ~ c))
Verifique a redução com uma tabela verdade
| fileira | Minterms | p | d | c | ( | ( | d | E | c | ) | ∨ | ( | p | E | d | ) | ∨ | ( | p | E | ~ | ( | c | ) | ) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | (~ p & ~ d & ~ c) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 1 | (~ p & ~ d & c) | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | |||||||||
| 2 | (~ p & d & ~ c) | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | |||||||||
| 3 | (~ p & d & c) | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | |||||||||
| 4 | (p & ~ d & ~ c) | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 5 | (p & ~ d & c) | 1 | 0 | 1 | 0 | 0 | 1 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | |||||||||
| 6 | (p & d & ~ c) | 1 | 1 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | |||||||||
| 7 | (p & d & c) | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | |||||||||
| q |
Proposições impredicativas
Dados os seguintes exemplos-como-definições, o que se pensa do raciocínio subsequente:
- (1) "Esta frase é simples." (2) "Esta frase é complexa e é conjunta por AND."
Em seguida, atribua a variável "s" à frase mais à esquerda "Esta frase é simples". Defina "composto" c = "não simples" ~ s e atribua c = ~ s a "Esta frase é composta"; atribua "j" a "It [esta frase] é conjunta por AND". A segunda frase pode ser expressa como:
- (NÃO (s) E j)
Se os valores verdadeiros devem ser colocados nas sentenças c = ~ sej, então todos são claramente FALSOSHAS: por exemplo, "Esta frase é complexa" é um FALSO (é simples , por definição). Portanto, sua conjunção (AND) é uma falsidade. Mas quando tomada em sua forma montada, a frase é uma VERDADE.
Este é um exemplo dos paradoxos que resultam de uma definição impredicativa - isto é, quando um objeto m tem uma propriedade P, mas o objeto m é definido em termos da propriedade P. O melhor conselho para um retórico ou alguém envolvido em análise dedutiva Isso evita definições impredicativas, mas, ao mesmo tempo, fica atento a elas porque elas podem, de fato, criar paradoxos. Os engenheiros, por outro lado, os colocam para trabalhar na forma de fórmulas proposicionais com feedback.
Fórmula proposicional com "feedback"
A noção de uma fórmula proposicional aparecendo como uma de suas próprias variáveis requer uma regra de formação que permite a atribuição da fórmula a uma variável. Em geral, não há estipulação (seja axiomático ou sistema de tabela de verdade de objetos e relações) que proíbe que isso aconteça.
O caso mais simples ocorre quando uma fórmula OR se torna uma de suas próprias entradas, por exemplo, p = q. Comece com (p ∨ s) = q, então seja p = q. Observe que a "definição" de q depende de si mesmo "q", bem como de "s" e do conectivo OR; esta definição de q é, portanto, impredicativa . Pode ocorrer uma das duas condições: oscilação ou memória.
Ajuda pensar na fórmula como uma caixa preta . Sem o conhecimento do que está acontecendo "dentro" da fórmula - "caixa" de fora, pareceria que a saída não é mais uma função apenas das entradas. Ou seja, às vezes olhamos para q e vemos 0 e outras vezes 1. Para evitar este problema, é necessário saber o estado (condição) da variável "oculta" p dentro da caixa (ou seja, o valor de q realimentado e atribuído a p). Quando isso é conhecido, a aparente inconsistência desaparece.
Para entender [prever] o comportamento das fórmulas com feedback, é necessária uma análise mais sofisticada de circuitos sequenciais . As fórmulas proposicionais com feedback levam, em sua forma mais simples, a máquinas de estados; eles também levam a memórias na forma de fitas de Turing e contadores de contra-máquina. A partir de combinações desses elementos, pode-se construir qualquer tipo de modelo computacional limitado (por exemplo , máquinas de Turing , máquinas de contador , máquinas de registro , computadores Macintosh , etc.).
Oscilação
No caso abstrato (ideal), a fórmula oscilante mais simples é um NÃO realimentado: ~ (~ (p = q)) = q. A análise de uma fórmula proposicional abstrata (ideal) em uma tabela de verdade revela uma inconsistência para ambos os casos p = 1 e p = 0: Quando p = 1, q = 0, isso não pode ser porque p = q; idem para quando p = 0 e q = 1.
| q | |||||||
|---|---|---|---|---|---|---|---|
| p | ~ | ( | p | ) | = q | ||
| 0 | 1 | 0 | 1 | q & p inconsistente | |||
| 1 | 0 | 1 | 0 | q & p inconsistente |
Oscilação com retardo : Se um retardo (ideal ou não ideal) é inserido na fórmula abstrata entre p e q então p irá oscilar entre 1 e 0: 101010 ... 101 ... ad infinitum . Se um dos atrasos e NOT não forem abstratos (ou seja, não ideais), o tipo de análise a ser usado dependerá da natureza exata dos objetos que compõem o oscilador; essas coisas estão fora da matemática e entram na engenharia.
A análise requer que um atraso seja inserido e, em seguida, o loop é cortado entre o atraso e a entrada "p". O atraso deve ser visto como um tipo de proposição que tem "qd" (q-delayed) como saída para "q" como entrada. Essa nova proposição adiciona outra coluna à tabela verdade. A inconsistência agora está entre "qd" e "p" conforme mostrado em vermelho; dois estados estáveis resultantes:
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| qd | p | ( | ~ | ( | p | ) | = q | |
| 0 | 0 | 1 | 0 | 1 | estado 1 | |||
| 0 | 1 | 0 | 1 | 0 | qd & p inconsistentes | |||
| 1 | 0 | 1 | 0 | 1 | qd & p inconsistentes | |||
| 1 | 1 | 0 | 1 | 0 | estado 0 |
Memória

Sem demora, as inconsistências devem ser eliminadas de uma análise de tabela verdade. Com a noção de "atraso", essa condição se apresenta como uma inconsistência momentânea entre a variável de saída do feedback q e p = q atrasada .
Uma tabela verdade revela as linhas onde ocorrem inconsistências entre p = q atrasado na entrada eq na saída. Depois de "quebrar" o feedback, a construção da tabela verdade prossegue da maneira convencional. Mas depois, em cada linha a saída q é comparada à entrada agora independente p e quaisquer inconsistências entre p e q são notadas (isto é, p = 0 junto com q = 1, ou p = 1 e q = 0); quando a "linha" é "refeita", ambas são tornadas impossíveis pela Lei da contradição ~ (p & ~ p)). As linhas que revelam inconsistências são consideradas estados transitórios ou simplesmente eliminadas como inconsistentes e, portanto, "impossíveis".
Memória Once-flip
Sobre os resultados de memória mais simples quando a saída de um OR realimenta uma de suas entradas, neste caso a saída "q" realimenta "p". Dado que a fórmula é avaliada primeiro (inicializada) com p = 0 & q = 0, ela "inverterá" uma vez quando "configurada" por s = 1. Depois disso, a saída "q" manterá "q" na condição "invertida" (estado q = 1). Este comportamento, agora dependente do tempo, é mostrado pelo diagrama de estado à direita da virada única.
| q | ||||||||
|---|---|---|---|---|---|---|---|---|
| p | s | ( | s | ∨ | p | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | estado 0, s = 0 | ||
| 0 | 1 | 1 | 1 | 0 | q & p inconsistente | |||
| 1 | 0 | 0 | 1 | 1 | 1 | estado 1 com s = 0 | ||
| 1 | 1 | 1 | 1 | 1 | 1 | estado 1 com s = 1 |
Memória flip-flop
O próximo caso mais simples é o flip-flop "set-reset" mostrado abaixo do flip-flop . Dado que r = 0 & s = 0 eq = 0 no início, é "definido" (s = 1) de maneira semelhante ao lançamento único. No entanto, tem uma disposição para "redefinir" q = 0 quando "r" = 1. E complicações adicionais ocorrem se ambos definirem = 1 e reiniciarem = 1. Nesta fórmula, o conjunto = 1 força a saída q = 1, portanto, quando e se (s = 0 & r = 1) o flip-flop será zerado. Ou, se (s = 1 & r = 0) o flip-flop será definido. Na instância abstrata (ideal) em que s = 1 ⇒ s = 0 & r = 1 ⇒ r = 0 simultaneamente, a fórmula q será indeterminada (indecidível). Devido a atrasos no "real" OR, AND e NOT, o resultado será desconhecido no início, mas depois disso previsível.
| q | ||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| p | s | r | ( | s | ∨ | ( | p | E | ~ | ( | r | ) | ) | ) | = q | |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | estado 0 com (s = 0 & r = 0) | ||||||
| 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | estado 0 com (s = 0 & r = 1) | ||||||
| 0 | 1 | 0 | 1 | 1 | 0 | 0 | 1 | 0 | q & p inconsistente | |||||||
| 0 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | q & p inconsistente | |||||||
| 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 1 | estado 1 com (s = 0 & r = 0) | ||||||
| 1 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | 1 | q & p inconsistente | |||||||
| 1 | 1 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 1 | estado 1 com (s = 1 & r = 0) | ||||||
| 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | estado 1 com s & r simultaneamente 1 |
Memória flip-flop sincronizada
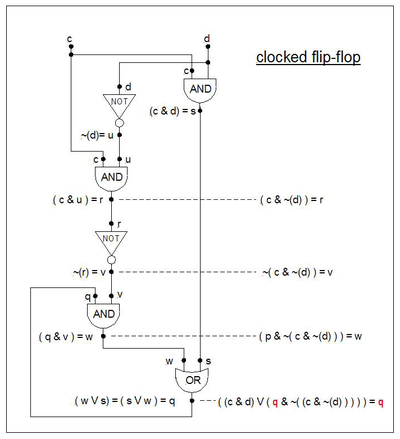
A fórmula conhecida como memória "flip-flop com clock" ("c" é o "relógio" e "d" é os "dados") é fornecida a seguir. Funciona da seguinte maneira: Quando c = 0, os dados d (0 ou 1) não podem "passar" para afetar a saída q. Quando c = 1, o dado d "passa" e a saída q "segue" o valor de d. Quando c vai de 1 a 0, o último valor dos dados permanece "preso" na saída "q". Enquanto c = 0, d pode alterar o valor sem causar a alteração de q.
- Exemplos
- ((c & d) ∨ ( p & (~ (c & ~ (d)))) = q , mas agora deixe p = q:
- ((c & d) ∨ ( q & (~ (c & ~ (d)))) = q
O diagrama de estado é semelhante ao diagrama de estado do flip-flop, mas com rótulos diferentes nas transições .
| s | q | C | v | r | você | |||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| fileira | q | d | c | ( | ( | c | E | d | ) | ∨ | ( | q | E | ~ | ( | ( | c | E | ~ | ( | d | ) | ) | ) | ) | ) | = q | Descrição |
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 0 | 0 | estado 0 com (s = 0 & r = 0), 0 está preso | ||||||||||||
| 1 | 0 | 0 | 1 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 0 | 0 | estado 0 com (d = 0 & c = 1): q = 0 segue d = 0 |
||||||||||||
| 2 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 1 | 0 | estado 0 com (d = 1 & r = 0), 0 está preso | ||||||||||||
| 3 | 0 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | 0 | 0 | 1 | q & p inconsistente | |||||||||||||
| 4 | 1 | 0 | 0 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 0 | 1 | estado 1 com (d = 0 & c = 0), 1 está preso | ||||||||||||
| 5 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 | 0 | 0 | 1 | 1 | 1 | 0 | q & p inconsistente | |||||||||||||
| 6 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 0 | 1 | 1 | estado 1 com (d = 1 & c = 0), 1 está preso | ||||||||||||
| 7 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 0 | 0 | 1 | 1 | estado 1 com (d = 1 & c = 1): q = 1 segue d = 1 |
Desenvolvimento histórico
Bertrand Russell (1912: 74) lista três leis de pensamento que derivam de Aristóteles : (1) A lei da identidade : "Tudo o que é, é.", (2) A lei da não - contradição : "Nada pode ser e não ser" , e (3) A lei do terceiro excluído : "Tudo deve ser ou não ser."
- Exemplo: Aqui, O é uma expressão sobre o SER ou QUALIDADE de um objeto:
- Lei da Identidade: O = O
- Lei da contradição: ~ (O & ~ (O))
- Lei do meio excluído: (O ∨ ~ (O))
O uso da palavra "tudo" na lei do terceiro excluído torna a expressão de Russell dessa lei aberta ao debate. Se restrito a uma expressão sobre SER ou QUALIDADE com referência a uma coleção finita de objetos (um "universo de discurso" finito) - cujos membros podem ser investigados um após o outro quanto à presença ou ausência da afirmação - então a lei é considerado intuicionisticamente apropriado. Portanto, uma afirmação como: "Este objeto deve SER ou NÃO SER (na coleção)", ou "Este objeto deve ter esta QUALIDADE ou NÃO ter esta QUALIDADE (em relação aos objetos na coleção)" é aceitável. Veja mais no diagrama de Venn .
Embora um cálculo proposicional tenha se originado com Aristóteles, a noção de uma álgebra aplicada a proposições teve que esperar até o início do século XIX. Em uma reação (adversa) à tradição de 2.000 anos dos silogismos de Aristóteles , o Ensaio de John Locke sobre a compreensão humana (1690) usou a palavra semiótica (teoria do uso de símbolos). Em 1826, Richard Whately analisou criticamente a lógica silogística com uma simpatia pela semiótica de Locke. O trabalho de George Bentham (1827) resultou na noção de "quantificação do predicado" (1827) (hoje simbolizado como ∀ ≡ "para todos"). Uma "briga" instigada por William Hamilton sobre uma disputa de prioridade com Augustus De Morgan "inspirou George Boole a escrever suas idéias sobre lógica e publicá-las como MAL [Análise Matemática da Lógica] em 1847" (Grattin-Guinness e Bornet 1997 : xxviii).
Sobre sua contribuição Grattin-Guinness e Bornet comentam:
- "A principal inovação de Boole foi [a] lei [x n = x] para a lógica: ela afirmava que os atos mentais de escolher a propriedade x e escolher x repetidamente é o mesmo que escolher x uma vez ... Como consequência disso ele formou as equações x • (1-x) = 0 ex + (1-x) = 1 que para ele expressavam respectivamente a lei da contradição e a lei do terceiro excluído "(p. xxviiff). Para Boole, "1" era o universo do discurso e "0" não era nada.
O empreendimento maciço de Gottlob Frege (1879) resultou em um cálculo formal de proposições, mas seu simbolismo é tão assustador que teve pouca influência, exceto em uma pessoa: Bertrand Russell . Primeiro, como aluno de Alfred North Whitehead, ele estudou a obra de Frege e sugeriu uma (famosa e notória) emenda a respeito dela (1904) em torno do problema de uma antinomia que ele descobriu no tratamento de Frege (cf. o paradoxo de Russell ). O trabalho de Russell levou a uma comparação com Whitehead que, no ano de 1912, produziu o primeiro volume de Principia Mathematica (PM). É aqui que o que consideramos lógica proposicional "moderna" apareceu pela primeira vez. Em particular, PM introduz NOT e OR e o símbolo de asserção ⊦ como primitivos. Em termos dessas noções, eles definem IMPLICAÇÃO → (def. * 1.01: ~ p ∨ q), então AND (def. * 3.01: ~ (~ p ∨ ~ q)), então EQUIVALÊNCIA p ← → q (* 4.01: ( p → q) & (q → p)).
- Henry M. Sheffer (1921) e Jean Nicod demonstram que apenas um conectivo, o "derrame" | é suficiente para expressar todas as fórmulas proposicionais.
- Emil Post (1921) desenvolve o método de análise da tabela de verdade em sua "Introdução a uma teoria geral das proposições elementares". Ele observa o derrame de Nicod | .
- Whitehead e Russell adicionam uma introdução à sua republicação de PM em 1927 adicionando, em parte, um tratamento favorável ao "derrame".
Computação e lógica de comutação :
- William Eccles e FW Jordan (1919) descrevem um "relé de gatilho" feito de um tubo de vácuo.
- George Stibitz (1937) inventa o somador binário usando relés mecânicos. Ele constrói isso na mesa da cozinha.
- Exemplo: Dados os bits binários a i e b i e carry-in (c_in i ), sua soma Σ i e carry-out (c_out i ) são:
- ((a i XOR b i ) XOR c_in i ) = Σ i
- (a i & b i ) ∨ c_in i ) = c_out i ;
- Alan Turing constrói um multiplicador usando relés (1937–1938). Ele tem que enrolar manualmente suas próprias bobinas de relé para fazer isso.
- Livros didáticos sobre "circuitos de comutação" aparecem no início dos anos 1950.
- Willard Quine 1952 e 1955, EW Veitch 1952 e M. Karnaugh (1953) desenvolvem métodos de mapas para simplificar funções proposicionais.
- George H. Mealy (1955) e Edward F. Moore (1956) abordam a teoria das "máquinas" sequenciais (isto é, circuitos de comutação).
- EJ McCluskey e H. Shorr desenvolveram um método para simplificar circuitos proposicionais (comutação) (1962).
Notas de rodapé
Referências
- Bender, Edward A. e Williamson, S. Gill , 2005, A Short Course in Discrete Mathematics , Dover Publications, Mineola NY, ISBN 0-486-43946-1 . Este texto é usado em um "curso de dois quartos de divisão inferior [ciência da computação]" na UC San Diego.
- Enderton, HB , 2002, A Mathematical Introduction to Logic. Harcourt / Academic Press. ISBN 0-12-238452-0
- Goodstein, RL , (Pergamon Press 1963), 1966, (Dover edition 2007), Boolean Algebra , Dover Publications, Inc. Minola, New York, ISBN 0-486-45894-6 . Ênfase na noção de "álgebra de classes" com símbolos teóricos de conjuntos como ∩, ∪, '(NOT), ⊂ (IMPLIES). Posteriormente, Goldstein os substitui por &, ∨, ¬, → (respectivamente) em seu tratamento da "Lógica da sentença", pp. 76-93.
- Ivor Grattan-Guinness e Gérard Bornet 1997, George Boole: Selected Manuscripts on Logic and its Philosophy , Birkhäuser Verlag, Basil, ISBN 978-0-8176-5456-6 (Boston).
- AG Hamilton 1978, Logic for Mathematicians , Cambridge University Press, Cambridge UK, ISBN 0-521-21838-1 .
- EJ McCluskey 1965, Introdução à Teoria dos Circuitos de Comutação , McGraw-Hill Book Company, Nova York. Sem ISBN. Número do cartão de catálogo da Biblioteca do Congresso 65-17394. McCluskey foi aluno de Willard Quine e desenvolveu alguns teoremas notáveis com Quine e por conta própria. Para os interessados na história, o livro contém uma riqueza de referências.
- Marvin L. Minsky 1967, Computation: Finite and Infinite Machines , Prentice-Hall, Inc, Englewood Cliffs, NJ. Sem ISBN. Número do cartão de catálogo da Biblioteca do Congresso 67-12342. Útil especialmente para computabilidade, além de boas fontes.
- Paul C. Rosenbloom 1950, edição de Dover 2005, The Elements of Mathematical Logic , Dover Publications, Inc., Mineola, New York, ISBN 0-486-44617-4 .
- Joel W. Robbin 1969, 1997, Mathematical Logic: A First Course , Dover Publications, Inc., Mineola, New York, ISBN 0-486-45018-X (pbk.).
- Patrick Suppes 1957 (edição de Dover de 1999), Introdução à lógica , Dover Publications, Inc., Mineola, Nova York. ISBN 0-486-40687-3 (pbk.). Este livro está impresso e disponível.
- Em sua página 204, em uma nota de rodapé, ele faz referência a seu conjunto de axiomas a EV Huntington , "Sets of Independent Postulates for the Algebra of Logic", Transactions of the American Mathematical Society, vol. 5 91904) pp. 288-309.
- Alfred Tarski 1941 (edição de Dover de 1995), Introdução à Lógica e à Metodologia das Ciências Dedutivas , Dover Publications, Inc., Mineola, Nova York. ISBN 0-486-28462-X (pbk.). Este livro está impresso e prontamente disponível.
- Jean van Heijenoort 1967, 3ª impressão com emendas 1976, From Frege to Gödel: A Source Book in Mathematical Logic, 1879-1931 , Harvard University Press, Cambridge, Massachusetts. ISBN 0-674-32449-8 (pbk.) Tradução / reimpressões de Frege (1879), carta de Russell para Frege (1902) e carta de Frege para Russell (1902), paradoxo de Richard (1905), Post (1921) podem ser encontrados aqui.
- Alfred North Whitehead e Bertrand Russell 1927 2ª edição, edição de bolso para * 53 1962, Principia Mathematica , Cambridge University Press, no ISBN. Nos anos entre a primeira edição de 1912 e a 2ª edição de 1927, HM Sheffer 1921 e M. Jean Nicod (nenhum ano citado) chamaram a atenção de Russell e Whitehead de que o que eles consideravam suas proposições primitivas (conectivos) poderiam ser reduzidas a um single |, hoje conhecido como "stroke" ou NAND (NOT-AND, NEITHER ... NOR ...). Russell-Whitehead discute isso em sua "Introdução à segunda edição" e faz as definições conforme discutido acima.
- William E. Wickes 1968, Logic Design with Integrated Circuits , John Wiley & Sons, Inc., Nova York. Sem ISBN. Número do cartão de catálogo da Biblioteca do Congresso: 68-21185. Apresentação rigorosa dos métodos de análise e síntese de engenharia, referências McCluskey 1965. Ao contrário de Suppes, a apresentação de Wickes da "álgebra booleana" começa com um conjunto de postulados de natureza de tabela de verdade e, em seguida, deriva os teoremas habituais deles (p. 18ss).
links externos
-
 Mídia relacionada à fórmula proposicional no Wikimedia Commons
Mídia relacionada à fórmula proposicional no Wikimedia Commons