Teorema de Pitágoras -Pythagorean theorem

Geometria
Projetando uma esfera para um plano
Contorno História
Galhos euclidiano Não-Euclidiano elíptico Esférico Hiperbólico Geometria não-arquimediana Projetivo afim Sintético Analítico Algébrico Aritmética Diofantina Diferencial Riemanniano Simples Diferencial discreto Complexo Finito Discreto/Combinatório Digital Convexo Computacional Fractal Incidência
Conceitos Recursos Dimensão Construções com régua e compasso Ângulo Curva Diagonal Ortogonalidade ( Perpendicular ) Paralelo Vértice Congruência Similaridade Simetria
Zero-dimensional Apontar
Unidimensional Linha segmento raio Comprimento
Bidimensional Plano Área Polígono Triângulo Altitude Hipotenusa teorema de Pitágoras Paralelogramo Praça Retângulo Losango Rombóide Quadrilátero trapézio Pipa Círculo Diâmetro Circunferência Área
Tridimensional Volume Cubo cubóide Cilindro Pirâmide Esfera
Quatro - / outras dimensões Tesseract Hiperesfera
Geômetros
por nome Aida Aryabhata Ahmes Alhazen Apolônio Arquimedes Atiyah Baudhayana Bolyai Brahmagupta Cartan Coxeter Descartes Euclides Euler Gauss Gromov Hilbert Jyeṣṭhadeva Katyayana Khayyam Klein Lobachevsky Manava Minkowski Minggatu Pascal Pitágoras Parameshvara Poincaré Riemann Sakabe Sijzi al-Tusi Veblen Virasena Yang Hui al-Yasamin Zhang Lista de geômetras
por período AEC Ahmes Baudhayana Manava Pitágoras Euclides Arquimedes Apolônio 1–1400s Zhang Katyayana Aryabhata Brahmagupta Virasena Alhazen Sijzi Khayyam al-Yasamin al-Tusi Yang Hui Parameshvara 1400-1700 Jyeṣṭhadeva Descartes Pascal Minggatu Euler Sakabe Aida 1700-1900 Gauss Lobachevsky Bolyai Riemann Klein Poincaré Hilbert Minkowski Cartan Veblen Coxeter Nos Dias de Hoje Atiyah Gromov
v t e

Em matemática , o teorema de Pitágoras , ou teorema de Pitágoras , é uma relação fundamental na geometria euclidiana entre os três lados de um triângulo retângulo . Ela afirma que a área do quadrado cujo lado é a hipotenusa (o lado oposto ao ângulo reto ) é igual à soma das áreas dos quadrados dos outros dois lados . Este teorema pode ser escrito como uma equação que relaciona os comprimentos dos lados a , b e c , muitas vezes chamada de equação de Pitágoras :

${\displaystyle a^{2}+b^{2}=c^{2},}$

onde c representa o comprimento da hipotenusa e aeb os comprimentos dos outros dois lados do triângulo. O teorema, cuja história é objeto de muito debate, recebeu o nome do filósofo grego Pitágoras , nascido por volta de 570 aC.

O teorema foi provado inúmeras vezes por muitos métodos diferentes – possivelmente o mais para qualquer teorema matemático. As provas são diversas, incluindo provas geométricas e provas algébricas, com algumas datando de milhares de anos.

O teorema pode ser generalizado de várias maneiras: para espaços de dimensão superior , para espaços que não são euclidianos , para objetos que não são triângulos retângulos e para objetos que não são triângulos, mas sólidos de n dimensões . O teorema de Pitágoras atraiu interesse fora da matemática como um símbolo de abstrusão matemática , mística ou poder intelectual; não faltam referências populares na literatura, peças de teatro, musicais, canções, selos e desenhos animados.

Prova de rearranjo

Cada um dos dois grandes quadrados mostrados na figura contém quatro triângulos idênticos, e a única diferença entre os dois grandes quadrados é que os triângulos estão dispostos de forma diferente. Portanto, o espaço em branco dentro de cada um dos dois quadrados grandes deve ter área igual. Equacionar a área do espaço em branco produz o teorema de Pitágoras, QED

O matemático inglês Sir Thomas Heath dá essa prova em seu comentário sobre a Proposição I.47 nos Elementos de Euclides , e menciona as propostas do alemão. matemáticos Carl Anton Bretschneider e Hermann Hankel que Pitágoras pode ter conhecido essa prova. O próprio Heath favorece uma proposta diferente para uma prova pitagórica, mas reconhece desde o início de sua discussão "que a literatura grega que possuímos pertencente aos primeiros cinco séculos após Pitágoras não contém nenhuma declaração especificando esta ou qualquer outra grande descoberta geométrica particular para ele. " Estudos recentes lançaram dúvidas crescentes sobre qualquer tipo de papel para Pitágoras como criador da matemática, embora o debate sobre isso continue.

Outras formas do teorema

Se c denota o comprimento da hipotenusa e a e b denotam os comprimentos dos outros dois lados, o teorema de Pitágoras pode ser expresso como a equação de Pitágoras:

${\displaystyle a^{2}+b^{2}=c^{2}.}$

Se os comprimentos de a e b são conhecidos, então c pode ser calculado como

${\displaystyle c={\sqrt {a^{2}+b^{2}}}.}$

Se o comprimento da hipotenusa c e de um lado ( a ou b ) são conhecidos, então o comprimento do outro lado pode ser calculado como

${\displaystyle a={\sqrt {c^{2}-b^{2}}}}$

ou

${\displaystyle b={\sqrt {c^{2}-a^{2}}}.}$

A equação de Pitágoras relaciona os lados de um triângulo retângulo de maneira simples, de modo que, se os comprimentos de quaisquer dois lados forem conhecidos, o comprimento do terceiro lado pode ser encontrado. Outro corolário do teorema é que em qualquer triângulo retângulo, a hipotenusa é maior que qualquer um dos outros lados, mas menor que sua soma.

Uma generalização deste teorema é a lei dos cossenos , que permite o cálculo do comprimento de qualquer lado de qualquer triângulo, dados os comprimentos dos outros dois lados e o ângulo entre eles. Se o ângulo entre os outros lados for um ângulo reto, a lei dos cossenos se reduz à equação de Pitágoras.

Outras provas do teorema

Esse teorema pode ter mais provas conhecidas do que qualquer outro (a lei da reciprocidade quadrática é outro candidato a essa distinção); o livro A Proposição Pitagórica contém 370 provas.

Demonstração usando triângulos semelhantes

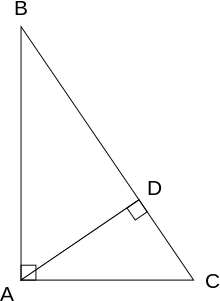
Esta prova baseia-se na proporcionalidade dos lados de dois triângulos semelhantes , ou seja, no fato de que a razão de quaisquer dois lados correspondentes de triângulos semelhantes é a mesma, independentemente do tamanho dos triângulos.

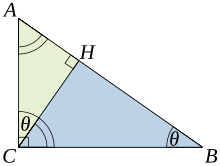
Seja ABC um triângulo retângulo, com o ângulo reto localizado em C , como mostra a figura. Desenhe a altitude do ponto C e chame H de sua interseção com o lado AB . O ponto H divide o comprimento da hipotenusa c em partes d e e . O novo triângulo, ACH, é semelhante ao triângulo ABC , porque ambos têm um ângulo reto (por definição da altitude) e compartilham o ângulo em A , o que significa que o terceiro ângulo será o mesmo em ambos os triângulos, marcado como θ na figura. Por um raciocínio semelhante, o triângulo CBH também é semelhante ao ABC . A prova da semelhança dos triângulos requer o postulado do triângulo : A soma dos ângulos em um triângulo é dois ângulos retos, e é equivalente ao postulado das paralelas . A semelhança dos triângulos leva à igualdade das razões dos lados correspondentes:

${\displaystyle {\frac {BC}{AB}}={\frac {BH}{BC}}{\text{ e }}{\frac {AC}{AB}}={\frac {AH}{AC }}.}$

O primeiro resultado iguala os cossenos dos ângulos θ , enquanto o segundo resultado iguala seus senos .

Essas proporções podem ser escritas como

${\displaystyle BC^{2}=AB\times BH{\text{ e }}AC^{2}=AB\times AH.}$

A soma dessas duas igualdades resulta em

${\displaystyle BC^{2}+AC^{2}=AB\times BH+AB\times AH=AB\times (AH+BH)=AB^{2},}$

que, após simplificação, expressa o teorema de Pitágoras:

${\displaystyle BC^{2}+AC^{2}=AB^{2}\ .}$

O papel dessa prova na história é objeto de muita especulação. A questão subjacente é por que Euclides não usou essa prova, mas inventou outra. Uma conjectura é que a prova por triângulos semelhantes envolvia uma teoria das proporções, um tópico não discutido até mais tarde nos Elementos , e que a teoria das proporções precisava de mais desenvolvimento naquele momento.

A prova de Euclides

Em linhas gerais, eis como procede a prova nos Elementos de Euclides . O quadrado grande é dividido em um retângulo esquerdo e direito. Um triângulo é construído que tem metade da área do retângulo esquerdo. Em seguida, outro triângulo é construído que tem metade da área do quadrado no lado mais à esquerda. Estes dois triângulos são congruentes , provando que este quadrado tem a mesma área que o retângulo da esquerda. Este argumento é seguido por uma versão semelhante para o retângulo direito e o quadrado restante. Colocando os dois retângulos juntos para reformar o quadrado na hipotenusa, sua área é igual à soma da área dos outros dois quadrados. Os detalhes seguem.

Sejam A , B , C os vértices de um triângulo retângulo, com um ângulo reto em A . Solte uma perpendicular de A ao lado oposto à hipotenusa no quadrado da hipotenusa. Essa linha divide o quadrado da hipotenusa em dois retângulos, cada um com a mesma área de um dos dois quadrados dos catetos.

Para a prova formal, exigimos quatro lemas elementares :

1. Se dois triângulos têm dois lados de um igual a dois lados do outro, cada um para cada um, e os ângulos incluídos por esses lados são iguais, então os triângulos são congruentes ( lado-ângulo-lado ).
2. A área de um triângulo é metade da área de qualquer paralelogramo sobre a mesma base e com a mesma altura.
3. A área de um retângulo é igual ao produto de dois lados adjacentes.
4. A área de um quadrado é igual ao produto de dois de seus lados (segue de 3).

Em seguida, cada quadrado superior está relacionado a um triângulo congruente com outro triângulo relacionado, por sua vez, a um dos dois retângulos que compõem o quadrado inferior.

A prova é a seguinte:

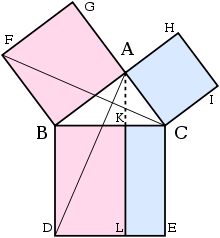
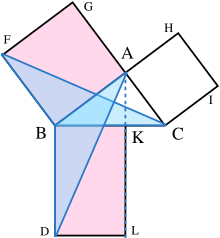
1. Seja ACB um triângulo retângulo com ângulo reto CAB.
2. Em cada um dos lados BC, AB e CA, são desenhados quadrados, CBDE, BAGF e ACIH, nessa ordem. A construção de quadrados requer os teoremas imediatamente anteriores em Euclides e depende do postulado das paralelas.
3. De A, desenhe uma linha paralela a BD e CE. Ele cruzará perpendicularmente BC e DE em K e L, respectivamente.
4. Junte CF e AD, para formar os triângulos BCF e BDA.
5. Os ângulos CAB e BAG são ambos ângulos retos; portanto C, A e G são colineares .
6. Os ângulos CBD e FBA são ambos ângulos retos; portanto, o ângulo ABD é igual ao ângulo FBC, pois ambos são a soma de um ângulo reto e um ângulo ABC.
7. Como AB é igual a FB, BD é igual a BC e o ângulo ABD é igual ao ângulo FBC, o triângulo ABD deve ser congruente ao triângulo FBC.
8. Como AKL é uma linha reta, paralela a BD, então o retângulo BDLK tem duas vezes a área do triângulo ABD porque eles compartilham a base BD e têm a mesma altura BK, ou seja, uma linha normal à sua base comum, conectando as linhas paralelas BD e AL. (lema 2)
9. Como C é colinear com A e G, e essa linha é paralela a FB, então o quadrado BAGF deve ter duas vezes a área do triângulo FBC.
10. Portanto, o retângulo BDLK deve ter a mesma área que o quadrado BAGF = AB ² .
11. Aplicando os passos 3 a 10 ao outro lado da figura, pode-se mostrar de forma semelhante que o retângulo CKLE deve ter a mesma área que o quadrado ACIH = AC ² .
12. Somando esses dois resultados, AB ² + AC ² = BD × BK + KL × KC
13. Como BD = KL, BD × BK + KL × KC = BD(BK + KC) = BD × BC
14. Portanto, AB ² + AC ² = BC ² , pois CBDE é um quadrado.

Esta prova, que aparece nos Elementos de Euclides como a da Proposição 47 no Livro 1, demonstra que a área do quadrado na hipotenusa é a soma das áreas dos outros dois quadrados. Isso é bastante distinto da prova por semelhança de triângulos, que é conjecturada como a prova que Pitágoras usou.

Provas por dissecção e rearranjo

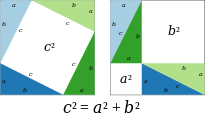
Já discutimos a prova pitagórica, que era uma prova por rearranjo. A mesma ideia é transmitida pela animação mais à esquerda abaixo, que consiste em um grande quadrado, lado a + b , contendo quatro triângulos retângulos idênticos. Os triângulos são mostrados em dois arranjos, o primeiro deixando dois quadrados a ² e b ² descobertos, o segundo deixando o quadrado c ² descoberto. A área abrangida pelo quadrado externo nunca muda, e a área dos quatro triângulos é a mesma no início e no final, então as áreas do quadrado preto devem ser iguais, portanto a ² + b ² = c ² .

Uma segunda prova por rearranjo é dada pela animação do meio. Um grande quadrado é formado com área c ² , a partir de quatro triângulos retângulos idênticos com lados a , b e c , encaixados em torno de um pequeno quadrado central. Então, dois retângulos são formados com lados a e b movendo os triângulos. A combinação do quadrado menor com esses retângulos produz dois quadrados de áreas a ² e b ² , que devem ter a mesma área do quadrado grande inicial.

A terceira imagem mais à direita também fornece uma prova. Os dois quadrados superiores são divididos como mostrado pelo sombreamento azul e verde, em pedaços que, quando rearranjados, podem ser feitos para caber no quadrado inferior na hipotenusa - ou, inversamente, o quadrado grande pode ser dividido como mostrado em pedaços que preenchem os outros dois . Essa maneira de cortar uma figura em pedaços e reorganizá-los para obter outra figura é chamada de dissecação . Isso mostra que a área do quadrado grande é igual à dos dois menores.

Animação mostrando a prova pelo rearranjo de quatro triângulos retângulos idênticos

Animação mostrando outra prova por rearranjo

Prova usando um rearranjo elaborado

A prova de Einstein por dissecação sem rearranjo

Albert Einstein deu uma prova por dissecação em que as peças não precisam ser movidas. Em vez de usar um quadrado na hipotenusa e dois quadrados nas pernas, pode-se usar qualquer outra forma que inclua a hipotenusa e duas formas semelhantes , cada uma incluindo uma das duas pernas em vez da hipotenusa (consulte Figuras semelhantes nos três lados ) . Na prova de Einstein, a forma que inclui a hipotenusa é o próprio triângulo retângulo. A dissecção consiste em soltar uma perpendicular do vértice do ângulo reto do triângulo até a hipotenusa, dividindo assim todo o triângulo em duas partes. Essas duas partes têm a mesma forma que o triângulo retângulo original e têm os catetos do triângulo original como suas hipotenusas, e a soma de suas áreas é a do triângulo original. Como a razão entre a área de um triângulo retângulo e o quadrado de sua hipotenusa é a mesma para triângulos semelhantes, a relação entre as áreas dos três triângulos também vale para os quadrados dos lados do triângulo grande.

Provas algébricas

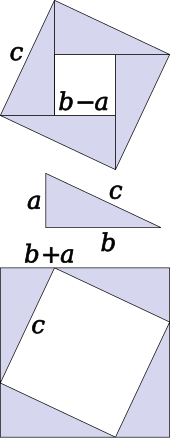
O teorema pode ser provado algebricamente usando quatro cópias de um triângulo retângulo de lados a , b e c , dispostos dentro de um quadrado de lado c como na metade superior do diagrama. Os triângulos são semelhantes com área , enquanto o pequeno quadrado tem lado b − a e área ( b − a ) ² . A área do quadrado grande é, portanto, ${\displaystyle {\tfrac {1}{2}}ab}$

${\displaystyle (ba)^{2}+4{\frac {ab}{2}}=(ba)^{2}+2ab=b^{2}-2ab+a^{2}+2ab=a ^{2}+b^{2}.}$

Mas este é um quadrado com lado c e área c ² , então

${\displaystyle c^{2}=a^{2}+b^{2}.}$

Uma prova semelhante usa quatro cópias do mesmo triângulo dispostas simetricamente em torno de um quadrado de lado c , como mostrado na parte inferior do diagrama. Isso resulta em um quadrado maior, com lado a + b e área ( a + b ) ² . Os quatro triângulos e o lado quadrado c devem ter a mesma área que o quadrado maior,

${\displaystyle (b+a)^{2}=c^{2}+4{\frac {ab}{2}}=c^{2}+2ab,}$

dando

${\displaystyle c^{2}=(b+a)^{2}-2ab=b^{2}+2ab+a^{2}-2ab=a^{2}+b^{2}.}$

Uma prova relacionada foi publicada pelo futuro presidente dos EUA James A. Garfield (então um representante dos EUA ) (veja o diagrama). Em vez de um quadrado, ele usa um trapézio , que pode ser construído a partir do quadrado na segunda das provas acima, dividindo-se ao longo de uma diagonal do quadrado interno, para obter o trapézio como mostrado no diagrama. A área do trapézio pode ser calculada como sendo metade da área do quadrado, ou seja,

${\displaystyle {\frac {1}{2}}(b+a)^{2}.}$

O quadrado interno é igualmente dividido pela metade, e há apenas dois triângulos, então a prova procede como acima, exceto por um fator de , que é removido multiplicando por dois para obter o resultado. ${\displaystyle {\frac {1}{2}}}$

Prova usando diferenciais

Pode-se chegar ao teorema de Pitágoras estudando como as mudanças em um lado produzem uma mudança na hipotenusa e empregando o cálculo .

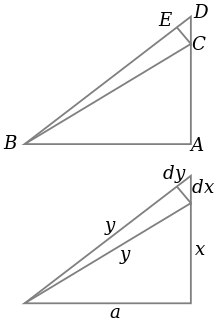
O triângulo ABC é um triângulo retângulo, como mostrado na parte superior do diagrama, sendo BC a hipotenusa. Ao mesmo tempo, os comprimentos dos triângulos são medidos como mostrado, com a hipotenusa de comprimento y , o lado AC de comprimento x e o lado AB de comprimento a , como visto na parte inferior do diagrama.

Se x é aumentado em uma pequena quantidade dx estendendo o lado AC ligeiramente para D , então y também aumenta em dy . Estes formam dois lados de um triângulo, CDE , que (com E escolhido para que CE seja perpendicular à hipotenusa) é um triângulo retângulo aproximadamente semelhante a ABC . Portanto, as razões de seus lados devem ser as mesmas, ou seja:

${\displaystyle {\frac {dy}{dx}}={\frac {x}{y}}.}$

Isso pode ser reescrito como , que é uma equação diferencial que pode ser resolvida por integração direta: ${\displaystyle y\,dy=x\,dx}$

${\displaystyle \int y\,dy=\int x\,dx\,,}$

dando

${\displaystyle y^{2}=x^{2}+C.}$

A constante pode ser deduzida de x = 0, y = a para dar a equação

${\displaystyle y^{2}=x^{2}+a^{2}.}$

Esta é uma prova mais intuitiva do que formal: pode ser mais rigorosa se forem usados ​​limites apropriados no lugar de dx e dy .

Conversar

A recíproca do teorema também é verdadeira:

Para quaisquer três números positivos a , b e c tais que a ² + b ² = c ² , existe um triângulo com lados a , b e c , e cada triângulo tem um ângulo reto entre os lados de comprimentos a e b .

Uma afirmação alternativa é:

Para qualquer triângulo com lados a , b , c , se a ² + b ² = c ² , então o ângulo entre a e b mede 90°.

Este inverso também aparece nos Elementos de Euclides (Livro I, Proposição 48):

"Se em um triângulo o quadrado de um dos lados é igual à soma dos quadrados dos dois lados restantes do triângulo, então o ângulo contido pelos dois lados restantes do triângulo é reto."

Pode ser provado usando a lei dos cossenos ou da seguinte forma:

Seja ABC um triângulo com lados de comprimento a , b e c , com a ² + b ² = c ² . Construa um segundo triângulo com lados de comprimento a e b contendo um ângulo reto. Pelo teorema de Pitágoras, segue-se que a hipotenusa deste triângulo tem comprimento c = √ a ² + b ² , o mesmo que a hipotenusa do primeiro triângulo. Como os lados de ambos os triângulos têm os mesmos comprimentos a , b e c , os triângulos são congruentes e devem ter os mesmos ângulos. Portanto, o ângulo entre os lados de comprimento a e b no triângulo original é um ângulo reto.

A prova da recíproca acima faz uso do próprio teorema de Pitágoras. A recíproca também pode ser provada sem assumir o teorema de Pitágoras.

Um corolário da recíproca do teorema de Pitágoras é um meio simples de determinar se um triângulo é reto, obtuso ou agudo, como segue. Seja c escolhido como o maior dos três lados e a + b > c (caso contrário, não há triângulo de acordo com a desigualdade triangular ). As seguintes afirmações se aplicam:

• Se a ² + b ² = c ² , então o triângulo é reto .
• Se a ² + b ² > c ² , então o triângulo é agudo .
• Se a ² + b ² < c ² , então o triângulo é obtuso .

Edsger W. Dijkstra declarou esta proposição sobre triângulos agudos, retos e obtusos nesta linguagem:

sgn( α + β − γ ) = sgn( a ² + b ² − c ² ),

onde α é o ângulo oposto ao lado a , β é o ângulo oposto ao lado b , γ é o ângulo oposto ao lado c e sgn é a função sinal .

Consequências e usos do teorema

triplos pitagóricos

Uma tripla pitagórica tem três inteiros positivos a , b e c , tais que a ² + b ² = c ² . Em outras palavras, uma tripla pitagórica representa os comprimentos dos lados de um triângulo retângulo onde todos os três lados têm comprimentos inteiros. Tal triplo é comumente escrito ( a , b , c ). Alguns exemplos bem conhecidos são (3, 4, 5) e (5, 12, 13).

Uma tripla pitagórica primitiva é aquela em que a , b e c são primos (o máximo divisor comum de a , b e c é 1).

A seguir está uma lista de triplos pitagóricos primitivos com valores menores que 100:

(3, 4, 5), (5, 12, 13), (7, 24, 25), (8, 15, 17), (9, 40, 41), (11, 60, 61), (12) , 35, 37), (13, 84, 85), (16, 63, 65), (20, 21, 29), (28, 45, 53), (33, 56, 65), (36, 77) , 85), (39, 80, 89), (48, 55, 73), (65, 72, 97)

Teorema de Pitágoras Recíproco

Dado um triângulo retângulo com lados e altura (uma linha do ângulo reto e perpendicular à hipotenusa ). O teorema de Pitágoras tem, ${\estilo de exibição a,b,c}$ ${\estilo de exibição d}$ ${\estilo de exibição c}$

${\displaystyle a^{2}+b^{2}=c^{2}}$

enquanto o teorema de Pitágoras recíproco ou o teorema de Pitágoras invertido relaciona as duas pernas com a altitude , ${\estilo de exibição a,b}$${\estilo de exibição d}$

${\displaystyle {\frac {1}{a^{2}}}+{\frac {1}{b^{2}}}={\frac {1}{d^{2}}}}$

A equação pode ser transformada para,

${\displaystyle {\frac {1}{(xz)^{2}}}+{\frac {1}{(yz)^{2}}}={\frac {1}{(xy)^{2 }}}}$

onde para qualquer real diferente de zero . Se forem inteiros , a menor solução é então ${\displaystyle x^{2}+y^{2}=z^{2}}$ ${\estilo de exibição x,y,z}$${\estilo de exibição a,b,d}$${\estilo de exibição a>b>d}$

${\displaystyle {\frac {1}{20^{2}}}+{\frac {1}{15^{2}}}={\frac {1}{12^{2}}}}$

usando o menor triplo pitagórico . O teorema de Pitágoras recíproca é um caso especial da equação óptica${\estilo de exibição 3,4,5}$

${\displaystyle {\frac {1}{p}}+{\frac {1}{q}}={\frac {1}{r}}}$

onde os denominadores são quadrados e também para um triângulo heptagonal cujos lados são números quadrados. ${\estilo de exibição p,q,r}$

Comprimentos incomensuráveis

Uma das consequências do teorema de Pitágoras é que segmentos de reta cujos comprimentos são incomensuráveis (portanto, cuja razão não é um número racional ) podem ser construídos com régua e compasso . O teorema de Pitágoras permite a construção de comprimentos incomensuráveis ​​porque a hipotenusa de um triângulo está relacionada aos lados pela operação da raiz quadrada .

A figura à direita mostra como construir segmentos de linha cujos comprimentos estão na razão da raiz quadrada de qualquer número inteiro positivo. Cada triângulo tem um lado (identificado como "1") que é a unidade de medida escolhida. Em cada triângulo retângulo, o teorema de Pitágoras estabelece o comprimento da hipotenusa em função dessa unidade. Se uma hipotenusa está relacionada à unidade pela raiz quadrada de um inteiro positivo que não é um quadrado perfeito, é uma realização de um comprimento incomensurável com a unidade, como √ 2 , √ 3 , √ 5  . Para obter mais detalhes, consulte Quadrático irracional .

Comprimentos incomensuráveis ​​conflitavam com o conceito de números da escola pitagórica como apenas números inteiros. A escola pitagórica lidava com proporções por comparação de múltiplos inteiros de uma subunidade comum. Segundo uma lenda, Hippasus de Metapontum ( ca. 470 aC) foi afogado no mar por dar a conhecer a existência do irracional ou incomensurável.

Números complexos

Para qualquer número complexo

${\displaystyle z=x+iy,}$

o valor absoluto ou módulo é dado por

${\displaystyle r=|z|={\sqrt {x^{2}+y^{2}}}.}$

Assim, as três quantidades, r , x e y estão relacionadas pela equação de Pitágoras,

${\displaystyle r^{2}=x^{2}+y^{2}.}$

Observe que r é definido como um número positivo ou zero, mas x e y podem ser tanto negativos quanto positivos. Geometricamente r é a distância do z de zero ou a origem O no plano complexo .

Isso pode ser generalizado para encontrar a distância entre dois pontos, z ₁ e z ₂ dizem. A distância necessária é dada por

${\displaystyle |z_{1}-z_{2}|={\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2} }},}$

então, novamente, eles estão relacionados por uma versão da equação de Pitágoras,

${\displaystyle |z_{1}-z_{2}|^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2} .}$

Distância euclidiana

A fórmula da distância em coordenadas cartesianas é derivada do teorema de Pitágoras. Se ( x ₁ , y ₁ ) e ( x ₂ , y ₂ ) são pontos no plano, então a distância entre eles, também chamada de distância euclidiana , é dada por

${\displaystyle {\sqrt {(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}}}.}$

Mais geralmente, no espaço n euclidiano , a distância euclidiana entre dois pontos, e , é definida, pela generalização do teorema de Pitágoras, como: ${\displaystyle A\,=\,(a_{1},a_{2},\dots ,a_{n})}$${\displaystyle B\,=\,(b_{1},b_{2},\dots ,b_{n})}$

${\displaystyle {\sqrt {(a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{ n})^{2}}}={\sqrt {\sum _{i=1}^{n}(a_{i}-b_{i})^{2}}}.}$

Se, em vez da distância euclidiana, for usado o quadrado desse valor (a distância euclidiana ao quadrado , ou SED), a equação resultante evita raízes quadradas e é simplesmente uma soma do SED das coordenadas:

${\displaystyle (a_{1}-b_{1})^{2}+(a_{2}-b_{2})^{2}+\cdots +(a_{n}-b_{n})^ {2}=\soma _{i=1}^{n}(a_{i}-b_{i})^{2}.}$

A forma quadrada é uma função suave e convexa de ambos os pontos, e é amplamente utilizada em teoria de otimização e estatística , formando a base dos mínimos quadrados .

Distância euclidiana em outros sistemas de coordenadas

Se não forem usadas coordenadas cartesianas, por exemplo, se forem usadas coordenadas polares em duas dimensões ou, em termos mais gerais, se forem usadas coordenadas curvilíneas , as fórmulas que expressam a distância euclidiana são mais complicadas que o teorema de Pitágoras, mas podem ser derivadas de isto. Um exemplo típico em que a distância em linha reta entre dois pontos é convertida em coordenadas curvilíneas pode ser encontrado nas aplicações dos polinômios de Legendre na física . As fórmulas podem ser descobertas usando o teorema de Pitágoras com as equações relacionando as coordenadas curvilíneas às coordenadas cartesianas. Por exemplo, as coordenadas polares ( r , θ ) podem ser introduzidas como:

${\displaystyle x=r\cos \theta ,\ y=r\sin \theta .}$

Então dois pontos com localizações ( r ₁ , θ ₁ ) e ( r ₂ , θ ₂ ) são separados por uma distância s :

${\displaystyle s^{2}=(x_{1}-x_{2})^{2}+(y_{1}-y_{2})^{2}=(r_{1}\cos \theta _{1}-r_{2}\cos \theta _{2})^{2}+(r_{1}\sin \theta _{1}-r_{2}\sin \theta _{2}) ^{2}.}$

Realizando os quadrados e combinando os termos, a fórmula pitagórica para distância em coordenadas cartesianas produz a separação em coordenadas polares como:

${\displaystyle {\begin{aligned}s^{2}&=r_{1}^{2}+r_{2}^{2}-2r_{1}r_{2}\left(\cos \theta _ {1}\cos \theta _{2}+\sin \theta _{1}\sin \theta _{2}\right)\\&=r_{1}^{2}+r_{2}^{ 2}-2r_{1}r_{2}\cos \left(\theta _{1}-\theta _{2}\right)\\&=r_{1}^{2}+r_{2}^ {2}-2r_{1}r_{2}\cos \Delta \theta ,\end{alinhado}}}$

usando as fórmulas trigonométricas de produto para soma . Esta fórmula é a lei dos cossenos , às vezes chamada de teorema de Pitágoras generalizado. A partir deste resultado, para o caso em que os raios para os dois locais são em ângulos retos, o ângulo fechado Δ θ = π /2, e a forma correspondente ao teorema de Pitágoras é recuperada: O teorema de Pitágoras, válido para triângulos retângulos, portanto é um caso especial da lei mais geral dos cossenos, válida para triângulos arbitrários. ${\displaystyle s^{2}=r_{1}^{2}+r_{2}^{2}.}$

identidade trigonométrica pitagórica

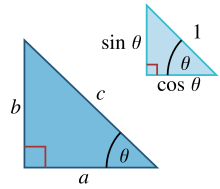
Em um triângulo retângulo com lados a , b e hipotenusa c , a trigonometria determina o seno e o cosseno do ângulo θ entre o lado a e a hipotenusa como:

${\displaystyle \sin \theta ={\frac {b}{c}},\quad \cos \theta ={\frac {a}{c}}.}$

A partir disso segue:

${\displaystyle {\cos }^{2}\theta +{\sin }^{2}\theta ={\frac {a^{2}+b^{2}}{c^{2}}}= 1,}$

onde o último passo aplica o teorema de Pitágoras. Essa relação entre seno e cosseno às vezes é chamada de identidade trigonométrica pitagórica fundamental. Em triângulos semelhantes, as razões dos lados são as mesmas, independentemente do tamanho dos triângulos, e dependem dos ângulos. Consequentemente, na figura, o triângulo com hipotenusa de tamanho unitário tem lado oposto de tamanho sen  θ e lado adjacente de tamanho cos  θ em unidades da hipotenusa.

Relação com o produto vetorial

O teorema de Pitágoras relaciona o produto vetorial e o produto escalar de maneira semelhante:

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}+(\mathbf {a} \cdot \mathbf {b} )^{2}=\|\mathbf {a} \|^{2}\|\mathbf{b} \|^{2}.}$

Isso pode ser visto a partir das definições de produto vetorial e produto escalar, como

${\displaystyle {\begin{alinhado}\mathbf {a} \times \mathbf {b} &=ab\mathbf {n} \sin {\theta }\\\mathbf {a} \cdot \mathbf {b} & =ab\cos {\theta },\end{alinhado}}}$

com n um vetor unitário normal a a e b . A relação decorre dessas definições e da identidade trigonométrica pitagórica.

Isso também pode ser usado para definir o produto cruzado. Reorganizando a seguinte equação é obtida

${\displaystyle \|\mathbf {a} \times \mathbf {b} \|^{2}=\|\mathbf {a} \|^{2}\|\mathbf {b} \|^{2} -(\mathbf {a} \cdot \mathbf {b} )^{2}.}$

Isso pode ser considerado como uma condição do produto vetorial e, portanto, parte de sua definição, por exemplo, em sete dimensões .

Generalizações

Figuras semelhantes nos três lados

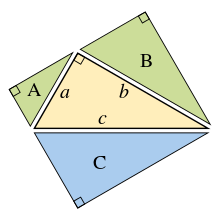
Uma generalização do teorema de Pitágoras que se estende além das áreas dos quadrados nos três lados para figuras semelhantes era conhecida por Hipócrates de Quios no século V aC, e foi incluída por Euclides em seus Elementos :

Se alguém erguer figuras semelhantes (ver geometria euclidiana ) com lados correspondentes nos lados de um triângulo retângulo, então a soma das áreas dos dois lados menores é igual à área do lado maior.

Essa extensão assume que os lados do triângulo original são os lados correspondentes das três figuras congruentes (portanto, as razões comuns dos lados entre as figuras semelhantes são a:b:c ). Enquanto a prova de Euclides se aplica apenas a polígonos convexos, o teorema também se aplica a polígonos côncavos e até mesmo a figuras semelhantes que têm limites curvos (mas ainda com parte do limite de uma figura sendo o lado do triângulo original).

A ideia básica por trás dessa generalização é que a área de uma figura plana é proporcional ao quadrado de qualquer dimensão linear e, em particular, é proporcional ao quadrado do comprimento de qualquer lado. Assim, se figuras semelhantes com áreas A , B e C são erguidas em lados com comprimentos correspondentes a , b e c então:

${\displaystyle {\frac {A}{a^{2}}}={\frac {B}{b^{2}}}={\frac {C}{c^{2}}}\,,, }$

${\displaystyle \Rightarrow A+B={\frac {a^{2}}{c^{2}}}C+{\frac {b^{2}}{c^{2}}}C\,. }$

Mas, pelo teorema de Pitágoras, a ² + b ² = c ² , então A + B = C .

Por outro lado, se pudermos provar que A + B = C para três figuras semelhantes sem usar o teorema de Pitágoras, podemos trabalhar para trás para construir uma prova do teorema. Por exemplo, o triângulo central inicial pode ser replicado e usado como um triângulo C em sua hipotenusa, e dois triângulos retângulos semelhantes ( A e B ) construídos nos outros dois lados, formados pela divisão do triângulo central por sua altura . A soma das áreas dos dois triângulos menores, portanto, é a do terceiro, assim A + B = C e invertendo a lógica acima leva ao teorema de Pitágoras a ² + b ² = c ² . ( Veja também a prova de Einstein por dissecação sem rearranjo )

Generalização para triângulos semelhantes, área verde A + B = área azul C

Teorema de Pitágoras usando triângulos retângulos semelhantes

Generalização para pentágonos regulares

Lei dos cossenos

O teorema de Pitágoras é um caso especial do teorema mais geral que relaciona os comprimentos dos lados em qualquer triângulo, a lei dos cossenos:

${\displaystyle a^{2}+b^{2}-2ab\cos {\theta }=c^{2},}$

onde é o ângulo entre os lados e . ${\ estilo de exibição \ theta }$${\ estilo de exibição a}$${\estilo de exibição b}$

Quando é radianos ou 90°, então , e a fórmula se reduz ao teorema de Pitágoras usual. ${\ estilo de exibição \ theta }$${\displaystyle {\frac {\pi }{2}}}$${\displaystyle \cos {\theta }=0}$

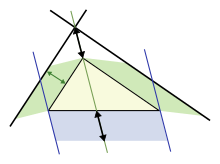
Triângulo arbitrário

Em qualquer ângulo selecionado de um triângulo geral de lados a, b, c , inscreva um triângulo isósceles tal que os ângulos iguais em sua base θ sejam os mesmos que o ângulo selecionado. Suponha que o ângulo selecionado θ seja oposto ao lado rotulado c . Inscrever o triângulo isósceles forma o triângulo CAD com ângulo θ oposto ao lado b e com lado r ao longo de c . Um segundo triângulo é formado com um ângulo θ oposto ao lado a e um lado de comprimento s ao longo de c , como mostra a figura. Thābit ibn Qurra afirmou que os lados dos três triângulos estavam relacionados como:

${\displaystyle a^{2}+b^{2}=c(r+s)\ .}$

À medida que o ângulo θ se aproxima de π /2, a base do triângulo isósceles se estreita e os comprimentos r e s se sobrepõem cada vez menos. Quando θ = π /2, ADB se torna um triângulo retângulo, r + s = c , e o teorema de Pitágoras original é recuperado.

Uma prova observa que o triângulo ABC tem os mesmos ângulos que o triângulo CAD , mas em ordem oposta. (Os dois triângulos compartilham o ângulo no vértice A, ambos contêm o ângulo θ e, portanto, também têm o mesmo terceiro ângulo pelo postulado do triângulo .) Consequentemente, ABC é semelhante à reflexão de CAD , o triângulo DAC no painel inferior. Tomando a razão dos lados opostos e adjacentes a θ,

${\displaystyle {\frac {c}{b}}={\frac {b}{r}}\ .}$

Da mesma forma, para a reflexão do outro triângulo,

${\displaystyle {\frac {c}{a}}={\frac {a}{s}}\ .}$

Limpando frações e somando essas duas relações:

${\displaystyle cs+cr=a^{2}+b^{2}\ ,}$

o resultado exigido.

O teorema permanece válido se o ângulo for obtuso, de modo que os comprimentos r e s não sejam sobrepostos. ${\ estilo de exibição \ theta }$

Triângulos gerais usando paralelogramos

O teorema da área de Pappus é uma generalização adicional, que se aplica a triângulos que não são triângulos retângulos, usando paralelogramos nos três lados no lugar de quadrados (os quadrados são um caso especial, é claro). A figura superior mostra que para um triângulo escaleno, a área do paralelogramo no lado maior é a soma das áreas dos paralelogramos nos outros dois lados, desde que o paralelogramo no lado maior seja construído como indicado (as dimensões marcadas com setas são as mesmas e determinam os lados do paralelogramo inferior). Esta substituição de quadrados por paralelogramos tem uma clara semelhança com o teorema de Pitágoras original, e foi considerada uma generalização por Pappus de Alexandria em 4 dC

A figura inferior mostra os elementos da prova. Concentre-se no lado esquerdo da figura. O paralelogramo verde esquerdo tem a mesma área que a porção azul esquerda do paralelogramo inferior porque ambos têm a mesma base b e altura h . No entanto, o paralelogramo verde esquerdo também tem a mesma área que o paralelogramo verde esquerdo da figura superior, porque eles têm a mesma base (o lado superior esquerdo do triângulo) e a mesma altura normal a esse lado do triângulo. Repetindo o argumento para o lado direito da figura, o paralelogramo inferior tem a mesma área que a soma dos dois paralelogramos verdes.

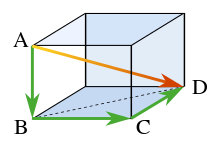
Geometria sólida

Em termos de geometria sólida, o teorema de Pitágoras pode ser aplicado a três dimensões como segue. Considere um sólido retangular como mostrado na figura. O comprimento da diagonal BD é encontrado a partir do teorema de Pitágoras como:

${\displaystyle {\overline {BD}}^{\,2}={\overline {BC}}^{\,2}+{\overline {CD}}^{\,2}\ ,}$

onde esses três lados formam um triângulo retângulo. Usando a diagonal horizontal BD e a aresta vertical AB , o comprimento da diagonal AD é então encontrado por uma segunda aplicação do teorema de Pitágoras como:

${\displaystyle {\overline {AD}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BD}}^{\,2}\ ,}$

ou, fazendo tudo em uma única etapa:

${\displaystyle {\overline {AD}}^{\,2}={\overline {AB}}^{\,2}+{\overline {BC}}^{\,2}+{\overline {CD }}^{\,2}\ .}$

Este resultado é a expressão tridimensional para a magnitude de um vetor v (a diagonal AD) em termos de seus componentes ortogonais { v _k } (os três lados mutuamente perpendiculares):

${\displaystyle \|\mathbf {v} \|^{2}=\sum _{k=1}^{3}\|\mathbf {v} _{k}\|^{2}.}$

Esta formulação de um passo pode ser vista como uma generalização do teorema de Pitágoras para dimensões superiores. No entanto, este resultado é realmente apenas a aplicação repetida do teorema de Pitágoras original a uma sucessão de triângulos retângulos em uma sequência de planos ortogonais.

Uma generalização substancial do teorema de Pitágoras para três dimensões é o teorema de Gua , nomeado em homenagem a Jean Paul de Gua de Malves : Se um tetraedro tem um canto de ângulo reto (como um canto de um cubo ), então o quadrado da área da face oposto ao canto do ângulo reto é a soma dos quadrados das áreas das outras três faces. Este resultado pode ser generalizado como no " teorema de Pitágoras n -dimensional":

Let Ser vetores ortogonais em ℝ ⁿ . Considere o simplex n -dimensional S com vértices . (Pense no simplex dimensional ( n  − 1) com vértices não incluindo a origem como a "hipotenusa" de S e as  faces dimensionais restantes ( n − 1) de S como suas "pernas".) Então o quadrado do o volume da hipotenusa de S é a soma dos quadrados dos volumes dos n catetos.${\displaystyle x_{1},x_{2},\ldots ,x_{n}}$${\displaystyle 0,x_{1},\ldots ,x_{n}}$${\displaystyle x_{1},\ldots ,x_{n}}$

Esta afirmação é ilustrada em três dimensões pelo tetraedro na figura. A "hipotenusa" é a base do tetraedro na parte de trás da figura, e as "pernas" são os três lados que emanam do vértice em primeiro plano. À medida que a profundidade da base do vértice aumenta, a área das "pernas" aumenta, enquanto a da base é fixa. O teorema sugere que quando esta profundidade está no valor criando um vértice direito, aplica-se a generalização do teorema de Pitágoras. Em outra redação:

Dado um simplex n - retangular n -dimensional, o quadrado do ( n  − 1)-conteúdo da faceta oposta ao vértice direito será igual à soma dos quadrados do ( n  − 1)-conteúdo das demais facetas.

Espaços de produtos internos

O teorema de Pitágoras pode ser generalizado para espaços de produto interno , que são generalizações dos familiares espaços euclidianos bidimensionais e tridimensionais . Por exemplo, uma função pode ser considerada como um vetor com infinitas componentes em um espaço de produto interno, como na análise funcional .

Em um espaço de produto interno, o conceito de perpendicularidade é substituído pelo conceito de ortogonalidade : dois vetores v e w são ortogonais se seu produto interno for zero. O produto interno é uma generalização do produto escalar de vetores. O produto escalar é chamado de produto interno padrão ou produto interno euclidiano . No entanto, outros produtos internos são possíveis. ${\displaystyle \langle \mathbf {v} ,\mathbf {w} \rangle }$

O conceito de comprimento é substituído pelo conceito de norma || v || de um vetor v , definido como:

${\ displaystyle \lVert \mathbf {v} \rVert \equiv {\sqrt {\langle \mathbf {v} ,\mathbf {v} \rangle }}\,.}$

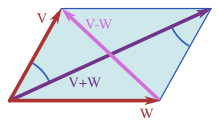
Em um espaço de produto interno, o teorema de Pitágoras afirma que para quaisquer dois vetores ortogonais v e w temos

${\displaystyle \left\|\mathbf {v} +\mathbf {w} \right\|^{2}=\left\|\mathbf {v} \right\|^{2}+\left\|\ mathbf {w} \right\|^{2}.}$

Aqui os vetores v e w são semelhantes aos lados de um triângulo retângulo com hipotenusa dada pela soma vetorial v  +  w . Esta forma do teorema de Pitágoras é uma consequência das propriedades do produto interno :

${\displaystyle \left\|\mathbf {v} +\mathbf {w} \right\|^{2}=\langle \mathbf {v+w} ,\ \mathbf {v+w} \rangle =\langle \mathbf {v} ,\ \mathbf {v} \rangle +\langle \mathbf {w} ,\ \mathbf {w} \rangle +\langle \mathbf {v,\w} \rangle +\langle \mathbf { w,\ v} \rangle \ =\left\|\mathbf {v} \right\|^{2}+\left\|\mathbf {w} \right\|^{2},}$

onde os produtos internos dos termos cruzados são zero, por causa da ortogonalidade.

Uma generalização adicional do teorema de Pitágoras em um espaço de produto interno para vetores não ortogonais é a lei do paralelogramo  :

${\displaystyle 2\|\mathbf {v} \|^{2}+2\|\mathbf {w} \|^{2}=\|\mathbf {v+w} \|^{2}+\ |\mathbf{vw} \|^{2}\,}$

que diz que duas vezes a soma dos quadrados dos comprimentos dos lados de um paralelogramo é a soma dos quadrados dos comprimentos das diagonais. Qualquer norma que satisfaça essa igualdade é ipso facto uma norma correspondente a um produto interno.

A identidade pitagórica pode ser estendida para somas de mais de dois vetores ortogonais. Se v ₁ , v ₂ , ..., v _n são vetores ortogonais aos pares em um espaço de produto interno, então a aplicação do teorema de Pitágoras a pares sucessivos desses vetores (como descrito para 3 dimensões na seção sobre geometria sólida ) resulta na equação

${\displaystyle \left\|\sum _{k=1}^{n}\mathbf {v} _{k}\right\|^{2}=\sum _{k=1}^{n}\ |\mathbf{v} _{k}\|^{2}}$

Conjuntos de objetos m -dimensionais no espaço n -dimensional

Outra generalização do teorema de Pitágoras se aplica a conjuntos de objetos mensuráveis ​​de Lebesgue em qualquer número de dimensões. Especificamente, o quadrado da medida de um conjunto m - dimensional de objetos em um ou mais planos m -dimensionais paralelos no espaço euclidiano n -dimensional é igual à soma dos quadrados das medidas das projeções ortogonais do(s) objeto(s). ) em todos os subespaços de coordenadas m -dimensionais.

Em termos matemáticos:

${\displaystyle \mu _{ms}^{2}=\sum _{i=1}^{x}\mathbf {\mu ^{2}} _{mp_{i}}}$

Onde:

• ${\estilo de exibição \mu _{m}}$é uma medida em m -dimensões (um comprimento em uma dimensão, uma área em duas dimensões, um volume em três dimensões, etc.).
• ${\displaystyle s}$é um conjunto de um ou mais objetos m -dimensionais não sobrepostos em um ou mais planos m -dimensionais paralelos no espaço euclidiano n -dimensional.
• ${\estilo de exibição \mu _{ms}}$é a medida total (soma) do conjunto de objetos m -dimensionais.
• ${\ estilo de exibição p}$representa uma projeção m - dimensional do conjunto original em um subespaço de coordenadas ortogonais.
• ${\displaystyle \mu _{mp_{i}}}$é a medida da projeção do conjunto m-dimensional no subespaço de coordenadas m -dimensional . Como as projeções de objetos podem se sobrepor em um subespaço de coordenadas, a medida de cada projeção de objeto no conjunto deve ser calculada individualmente e, em seguida, as medidas de todas as projeções somadas para fornecer a medida total do conjunto de projeções no subespaço de coordenadas fornecido.${\estilo de exibição i}$
• ${\estilo de exibição x}$é o número de subespaços de coordenadas ortogonais m -dimensionais no espaço n -dimensional ( R ⁿ ) no qual os objetos m -dimensionais são projetados ( m ≤ n ):

${\displaystyle x={\binom {n}{m}}={\frac {n!}{m!(nm)!}}}$

Geometria não euclidiana

O teorema de Pitágoras é derivado dos axiomas da geometria euclidiana e, de fato, se o teorema de Pitágoras falhar para algum triângulo retângulo, então o plano no qual esse triângulo está contido não pode ser euclidiano. Mais precisamente, o teorema de Pitágoras implica e está implícito no Postulado das Paralelas (Quinto) de Euclides . Assim, triângulos retângulos em uma geometria não-euclidiana não satisfazem o teorema de Pitágoras. Por exemplo, na geometria esférica , todos os três lados do triângulo retângulo (digamos a , b e c ) limitando um octante da esfera unitária têm comprimento igual a π /2, e todos os seus ângulos são ângulos retos, o que viola o pitagórico teorema porque . ${\displaystyle a^{2}+b^{2}=2c^{2}>c^{2}}$

Aqui são considerados dois casos de geometria não-euclidiana – geometria esférica e geometria plana hiperbólica ; em cada caso, como no caso euclidiano para triângulos não retângulos, o resultado substituindo o teorema de Pitágoras segue da lei apropriada dos cossenos.

No entanto, o teorema de Pitágoras permanece verdadeiro na geometria hiperbólica e na geometria elíptica se a condição de que o triângulo seja reto for substituída pela condição de que dois dos ângulos somam ao terceiro, digamos A + B = C . Os lados são então relacionados da seguinte forma: a soma das áreas dos círculos com diâmetros aeb é igual à área do círculo com diâmetro c .

Geometria esférica

Para qualquer triângulo retângulo em uma esfera de raio R (por exemplo, se γ na figura é um ângulo reto), com lados a , b , c , a relação entre os lados assume a forma:

${\displaystyle \cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cos \left({\frac {b }{R}}\direito).}$

Esta equação pode ser derivada como um caso especial da lei esférica dos cossenos que se aplica a todos os triângulos esféricos:

${\displaystyle \cos \left({\frac {c}{R}}\right)=\cos \left({\frac {a}{R}}\right)\cos \left({\frac {b }{R}}\right)+\sin \left({\frac {a}{R}}\right)\sin \left({\frac {b}{R}}\right)\cos \gamma \ .}$

Expressando a série de Maclaurin para a função cosseno como uma expansão assintótica com o termo restante em notação O grande ,

${\displaystyle \cos x=1-{\frac {x^{2}}{2}}+O(x^{4}){\text{ as }}x\to 0\ ,}$

pode-se mostrar que à medida que o raio R se aproxima do infinito e os argumentos a/R , b/R e c/R tendem a zero, a relação esférica entre os lados de um triângulo retângulo se aproxima da forma euclidiana do teorema de Pitágoras. Substituindo a expansão assintótica para cada um dos cossenos na relação esférica para um triângulo retângulo, obtém-se

${\displaystyle 1-{\frac {1}{2}}\left({\frac {c}{R}}\right)^{2}+O\left({\frac {1}{R^{ 4}}}\right)=\left[1-{\frac {1}{2}}\left({\frac {a}{R}}\right)^{2}+O\left({\ frac {1}{R^{4}}}\right)\right]\left[1-{\frac {1}{2}}\left({\frac {b}{R}}\right)^ {2}+O\left({\frac {1}{R^{4}}}\right)\right]{\text{ as }}R\to \infty \ .}$

As constantes a ⁴ , b ⁴ e c ⁴ foram absorvidas nos grandes termos de resto O já que são independentes do raio R . Essa relação assintótica pode ser simplificada ainda mais multiplicando as quantidades entre colchetes, cancelando as unidades, multiplicando por -2 e reunindo todos os termos de erro:

${\displaystyle \left({\frac {c}{R}}\right)^{2}=\left({\frac {a}{R}}\right)^{2}+\left({\ frac {b}{R}}\right)^{2}+O\left({\frac {1}{R^{4}}}\right){\text{ as }}R\to \infty \ .}$

Depois de multiplicar por R ² , a relação euclidiana pitagórica c ² = a ² + b ² é recuperada no limite à medida que o raio R se aproxima do infinito (já que o termo restante tende a zero):

${\displaystyle c^{2}=a^{2}+b^{2}+O\left({\frac {1}{R^{2}}}\right){\text{ as }}R \to \infty\ .}$

Para pequenos triângulos retângulos ( a , b << R ), os cossenos podem ser eliminados para evitar perda de significância , dando

${\displaystyle \sin ^{2}{\frac {c}{2R}}=\sin ^{2}{\frac {a}{2R}}+\sin ^{2}{\frac {b}{ 2R}}-2\sin ^{2}{\frac {a}{2R}}\sin ^{2}{\frac {b}{2R}}\,.}$

Geometria hiperbólica

Em um espaço hiperbólico com curvatura uniforme −1/ R ² , para um triângulo retângulo com catetos a , b , e hipotenusa c , a relação entre os lados toma a forma:

${\displaystyle \cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\,\cosh {\frac {b}{R}}}$

onde cosh é o cosseno hiperbólico . Esta fórmula é uma forma especial da lei hiperbólica dos cossenos que se aplica a todos os triângulos hiperbólicos:

${\displaystyle \cosh {\frac {c}{R}}=\cosh {\frac {a}{R}}\ \cosh {\frac {b}{R}}-\sinh {\frac {a} {R}}\ \sinh {\frac {b}{R}}\ \cos \gamma \ ,}$

com γ o ângulo no vértice oposto ao lado c .

Usando a série de Maclaurin para o cosseno hiperbólico, cosh x ≈ 1 + x ² /2 , pode-se mostrar que à medida que um triângulo hiperbólico se torna muito pequeno (isto é, quando a , b e c se aproximam de zero), o triângulo hiperbólico relação para um triângulo retângulo se aproxima da forma do teorema de Pitágoras.

Para pequenos triângulos retângulos ( a , b << R ), os cossenos hiperbólicos podem ser eliminados para evitar perda de significância , dando

${\displaystyle \sinh ^{2}{\frac {c}{2R}}=\sinh ^{2}{\frac {a}{2R}}+\sinh ^{2}{\frac {b}{ 2R}}+2\sinh ^{2}{\frac {a}{2R}}\sinh ^{2}{\frac {b}{2R}}\,.}$

Triângulos muito pequenos

Para qualquer curvatura uniforme K (positiva, zero ou negativa), em triângulos retângulos muito pequenos (| K | a ² , | K | b ² << 1) com hipotenusa c , pode-se mostrar que

${\displaystyle c^{2}=a^{2}+b^{2}-{\frac {K}{3}}a^{2}b^{2}-{\frac {K^{2 }}{45}}a^{2}b^{2}(a^{2}+b^{2})-{\frac {2K^{3}}{945}}a^{2}b ^{2}(a^{2}-b^{2})^{2}+O(K^{4}c^{10})\,.}$

Geometria diferencial

Em um nível infinitesimal, no espaço tridimensional, o teorema de Pitágoras descreve a distância entre dois pontos separados infinitesimalmente como:

${\displaystyle ds^{2}=dx^{2}+dy^{2}+dz^{2},}$

com ds o elemento da distância e ( dx , dy , dz ) as componentes do vetor que separa os dois pontos. Esse espaço é chamado de espaço euclidiano . No entanto, na geometria Riemanniana , uma generalização desta expressão útil para coordenadas gerais (não apenas cartesianas) e espaços gerais (não apenas euclidianas) assume a forma:

${\displaystyle ds^{2}=\sum _{i,j}^{n}g_{ij}\,dx_{i}\,dx_{j}}$

que é chamado de tensor métrico . (Às vezes, por abuso de linguagem, o mesmo termo é aplicado ao conjunto de coeficientes g _ij .) Pode ser uma função da posição e muitas vezes descreve o espaço curvo . Um exemplo simples é o espaço euclidiano (plano) expresso em coordenadas curvilíneas . Por exemplo, em coordenadas polares :

${\displaystyle ds^{2}=dr^{2}+r^{2}d\theta ^{2}\ .}$

História

Há debate se o teorema de Pitágoras foi descoberto uma vez, ou muitas vezes em muitos lugares, e a data da primeira descoberta é incerta, assim como a data da primeira prova. Os historiadores da matemática mesopotâmica concluíram que o domínio pitagórico estava em uso generalizado durante o período babilônico antigo (séculos 20 a 16 aC), mais de mil anos antes do nascimento de Pitágoras. A história do teorema pode ser dividida em quatro partes: conhecimento dos triplos pitagóricos , conhecimento da relação entre os lados de um triângulo retângulo, conhecimento das relações entre ângulos adjacentes e demonstrações do teorema dentro de algum sistema dedutivo .

Escrito entre 2000 e 1786 aC, o Papiro de Berlim do Reino Médio Egípcio 6619 inclui um problema cuja solução é o triplo pitagórico 6:8:10, mas o problema não menciona um triângulo. A tabuleta mesopotâmica Plimpton 322 , escrita entre 1790 e 1750 aC durante o reinado do rei Hamurabi , o Grande, contém muitas entradas intimamente relacionadas aos triplos pitagóricos.

Na Índia , o Baudhayana Shulba Sutra , cujas datas são dadas variadamente entre os séculos VIII e V aC, contém uma lista de triplos pitagóricos e uma declaração do teorema de Pitágoras, tanto no caso especial do triângulo retângulo isósceles quanto no o caso geral, assim como o Apastamba Shulba Sutra (c. 600 aC).

O filósofo e matemático neoplatônico bizantino Proclo , escrevendo no século V dC, afirma duas regras aritméticas, "uma delas atribuída a Platão , a outra a Pitágoras", para gerar triplos pitagóricos especiais. A regra atribuída a Pitágoras ( c.  570  – c.  495 aC ) parte de um número ímpar e produz um triplo com cateto e hipotenusa diferindo por uma unidade; a regra atribuída a Platão (428/427 ou 424/423 – 348/347 aC) parte de um número par e produz um triplo com cateto e hipotenusa diferindo por duas unidades. De acordo com Thomas L. Heath (1861-1940), nenhuma atribuição específica do teorema a Pitágoras existe na literatura grega sobrevivente dos cinco séculos após a vida de Pitágoras. No entanto, quando autores como Plutarco e Cícero atribuíram o teorema a Pitágoras, eles o fizeram de uma forma que sugere que a atribuição era amplamente conhecida e indubitável. O classicista Kurt von Fritz escreveu: "Se esta fórmula é corretamente atribuída a Pitágoras pessoalmente, mas pode-se supor com segurança que ela pertence ao período mais antigo da matemática pitagórica ". Por volta de 300 aC, nos Elementos de Euclides, é apresentada a mais antiga prova axiomática existente do teorema.

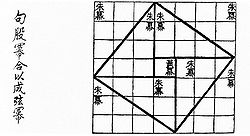
Com conteúdo conhecido muito antes, mas em textos sobreviventes que datam aproximadamente do século I a.C., o texto chinês Zhoubi Suanjing (周髀算经), ( O Clássico Aritmético do Gnômon e os Caminhos Circulares do Céu ) dá um raciocínio para o pitagórico teorema para o triângulo (3, 4, 5) — na China é chamado de " teorema de Gougu " (勾股定理). Durante a Dinastia Han (202 aC a 220 dC), os triplos pitagóricos aparecem nos Nove Capítulos da Arte Matemática , juntamente com uma menção aos triângulos retângulos. Alguns acreditam que o teorema surgiu primeiro na China , onde é alternativamente conhecido como o " teorema de Shang Gao " (商高定理), em homenagem ao astrônomo e matemático do duque de Zhou , cujo raciocínio compôs a maior parte do que estava no Zhoubi Suanjing .

Veja também

Notas e referências

Notas

Referências

Trabalhos citados

links externos

• Teorema de Pitágoras na ProofWiki

• Euclides (1997) [c. 300 aC]. David E. Joyce (ed.). Elementos . Recuperado em 30-08-2006 .Em HTML com figuras interativas baseadas em Java.
• "Teorema de Pitágoras" . Enciclopédia de Matemática . Pressione EMS . 2001 [1994].
• Tópico de história: o teorema de Pitágoras na matemática babilônica
• Links interativos:
  • Prova interativa em Java do teorema de Pitágoras
  • Outra prova interativa em Java do teorema de Pitágoras
  • Teorema de Pitágoras com animação interativa
  • Teorema de Pitágoras animado, não algébrico e controlado pelo usuário
• Demonstração da água do teorema de Pitágoras no YouTube
• Teorema de Pitágoras (mais de 70 provas de cut-the-knot )
• Weisstein, Eric W. "Teorema de Pitágoras" . MathWorld .