Triplo pitagórico - Pythagorean triple
Um triplo pitagórico consiste em três inteiros positivos a , b e c , de modo que a 2 + b 2 = c 2 . Tal triplo é comumente escrito ( a , b , c ) , e um exemplo bem conhecido é (3, 4, 5) . Se ( a , b , c ) é um triplo pitagórico, então o é ( ka , kb , kc ) para qualquer inteiro positivo k . Um Pitágoras primitivo triplo é um em que um , b e c são primos entre si (isto é, eles não têm divisor comum maior do que 1). Um triângulo cujos lados formam um triplo pitagórico é chamado de triângulo pitagórico e é necessariamente um triângulo retângulo .
O nome é derivado do teorema de Pitágoras , afirmando que todo triângulo retângulo tem comprimentos de lado que satisfazem a fórmula a 2 + b 2 = c 2 ; assim, os triplos pitagóricos descrevem os três comprimentos laterais inteiros de um triângulo retângulo. No entanto, triângulos retângulos com lados não inteiros não formam triplos pitagóricos. Por exemplo, o triângulo com lados um = b = 1 e c = √ 2 é um triângulo rectângulo, mas (1, 1, √ 2 ) não é uma Pitágoras triplo porque √ 2 não é um número inteiro. Além disso, 1 e √ 2 não têm um múltiplo comum inteiro porque √ 2 é irracional .
Os triplos pitagóricos são conhecidos desde os tempos antigos. O registro mais antigo conhecido vem de Plimpton 322 , uma tábua de argila babilônica de cerca de 1800 aC, escrita em um sistema numérico sexagesimal . Foi descoberto por Edgar James Banks pouco depois de 1900 e vendido a George Arthur Plimpton em 1922 por $ 10.
Ao pesquisar soluções inteiras, a equação a 2 + b 2 = c 2 é uma equação Diofantina . Assim, os triplos pitagóricos estão entre as soluções mais antigas conhecidas de uma equação diofantina não linear.
Exemplos
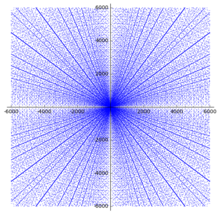
Existem 16 triplos pitagóricos primitivos de números até 100:
| (3, 4, 5) | (5, 12, 13) | (8, 15, 17) | (7, 24, 25) |
| (20, 21, 29) | (12, 35, 37) | (9, 40, 41) | (28, 45, 53) |
| (11, 60, 61) | (16, 63, 65) | (33, 56, 65) | (48, 55, 73) |
| (13, 84, 85) | (36, 77, 85) | (39, 80, 89) | (65, 72, 97) |
Cada um desses pontos forma uma linha radiante no gráfico de dispersão. Outros pequenos triplos pitagóricos, como (6, 8, 10) não são listados porque não são primitivos; por exemplo (6, 8, 10) é um múltiplo de (3, 4, 5).
Além disso, estes são os triplos pitagóricos primitivos restantes de números até 300:
| (20, 99, 101) | (60, 91, 109) | (15, 112, 113) | (44, 117, 125) |
| (88, 105, 137) | (17, 144, 145) | (24, 143, 145) | (51, 140, 149) |
| (85, 132, 157) | (119, 120, 169) | (52, 165, 173) | (19, 180, 181) |
| (57, 176, 185) | (104, 153, 185) | (95, 168, 193) | (28, 195, 197) |
| (84, 187, 205) | (133, 156, 205) | (21, 220, 221) | (140, 171, 221) |
| (60, 221, 229) | (105, 208, 233) | (120, 209, 241) | (32, 255, 257) |
| (23, 264, 265) | (96, 247, 265) | (69, 260, 269) | (115, 252, 277) |
| (160, 231, 281) | (161, 240, 289) | (68, 285, 293) |
Gerando um triplo

Fórmula de Euclides é uma fórmula fundamental para a geração de triplos de Pitágoras dado um par arbitrária de inteiros m e n com m > n > 0 . A fórmula afirma que os inteiros
formam um triplo pitagórico. O triplo gerado pela fórmula de Euclides é primitivo se e somente se m e n são coprimos e não ambos ímpares. Quando m e n são ímpares, a , b e c serão pares e o triplo não será primitivo; entretanto, dividir a , b e c por 2 resultará em um triplo primitivo quando m e n são coprimos e ambos ímpares.
Cada triplo primitivo surge (após a troca de um e b , se uma é mesmo) a partir de um único par de números coprimas m , n , um dos quais é mesmo. Segue-se que há infinitamente muitos triplos pitagóricos primitivos. Esta relação de um , b e c a m e n a partir da fórmula de Euclides é referenciado em toda a restante deste artigo.
Apesar gerando todos os triplos primitivas, fórmula de Euclides não produz todos os triplos, por exemplo, (9, 12, 15) não pode ser gerado usando inteiro m e n . Isso pode ser remediado inserindo um parâmetro adicional k à fórmula. O seguinte irá gerar todos os triplos pitagóricos exclusivamente:
onde m , n e k são inteiros positivos com m > n e com coprime m e n e não ambos ímpares.
Que essas fórmulas geram triplas pitagóricas pode ser verificado expandindo a 2 + b 2 usando álgebra elementar e verificando se o resultado é igual a c 2 . Uma vez que cada triplo pitagórico pode ser dividido por algum inteiro k para obter um triplo primitivo, cada triplo pode ser gerado exclusivamente usando a fórmula com m e n para gerar sua contraparte primitiva e, em seguida, multiplicando por k como na última equação.
Escolhendo m e n a partir de certas sequências inteiros dá resultados interessantes. Por exemplo, se m e n forem números Pell consecutivos , a e b serão diferentes em 1.
Muitas fórmulas para gerar triplas com propriedades particulares foram desenvolvidas desde a época de Euclides.
Prova da fórmula de Euclides
Que a satisfação da fórmula de Euclides por a, b, c é suficiente para o triângulo ser pitagórico é aparente pelo fato de que para inteiros positivos m e n , m > n , a , b e c dados pela fórmula são todos positivos inteiros, e do fato de que
Uma prova da necessidade de que a, b, c sejam expressos pela fórmula de Euclides para qualquer tríplice pitagórica primitiva é a seguinte. Todos esses triplos primitivos podem ser escritos como ( a , b , c ) onde a 2 + b 2 = c 2 e a , b , c são coprimos . Assim , a , b , c são coprimos de pares (se um número primo dividisse dois deles, seria forçado também a dividir o terceiro). Como a e b são coprimos, pelo menos um deles é ímpar, então podemos supor que a é ímpar trocando, se necessário, a e b . Isso implica que b é par e c é ímpar (se b fosse ímpar, c seria par e c 2 seria um múltiplo de 4, enquanto a 2 + b 2 seria congruente a 2 módulo 4, pois um quadrado ímpar é congruente a 1 módulo 4).
De nós obtemos e, portanto . Então . Uma vez que é racional, nós o definimos como nos termos mais baixos. Portanto , sendo o recíproco de . Então resolvendo
para e dá
Como está totalmente reduzido, m e n são coprimos e não podem ser ambos iguais. Se ambos fossem ímpares, o numerador de seria um múltiplo de 4 (porque um quadrado ímpar é congruente com 1 módulo 4), e o denominador 2 mn não seria um múltiplo de 4. Visto que 4 seria o fator par mínimo possível no numerador e 2 seria o fator ainda possível máxima no denominador, isto implicaria um ser ainda apesar definindo-o como estranho. Assim, um dos m e n é ímpar e o outro é o mesmo, e as numeradas das duas fracções com denominador 2 mn são estranho. Assim, estas fracções são totalmente reduzida (um primo ímpar dividindo Isto divide um denominador de m e n , mas não a outra; assim, não se divide m 2 ± n 2 ). Pode-se, portanto, igualar numeradores com numeradores e denominadores com denominadores, dando a fórmula de Euclides
- com m e n primos entre si e das paridades opostas.
Uma prova mais longa, mas mais comum, é fornecida em Maor (2007) e Sierpiński (2003). Outra prova é dada na equação diofantina § Exemplo de triplas pitagóricas , como uma instância de um método geral que se aplica a toda equação diofantina homogênea de grau dois.
Interpretação de parâmetros na fórmula de Euclides
Suponha que os lados de um triângulo pitagórico tenham comprimentos m 2 - n 2 , 2 mn e m 2 + n 2 , e suponha que o ângulo entre a perna de comprimento m 2 - n 2 e a hipotenusa de comprimento m 2 + n 2 é denotado como β . Então eo full-ângulo valores trigonométricas são , e .
Uma variante
O seguinte variante de fórmula de Euclides é por vezes mais conveniente, como sendo mais simétrica em m e n (mesma condição de paridade em m e n ).
Se m e n são dois inteiros ímpares, tais que m > n , então
são três inteiros que formam uma tripla pitagórica, que é primitiva se e somente se m e n são coprimos. Por outro lado, cada primitiva de Pitágoras surge triplo (após a troca de um e b , se uma é mesmo) a partir de um único par m > n > 0 de coprimas inteiros impares.
Propriedades elementares de triplos pitagóricos primitivos
Propriedades gerais
As propriedades de um triplo pitagórico primitivo ( a , b , c ) com a < b < c (sem especificar qual de a ou b é par e qual é ímpar) incluem:
- é sempre um quadrado perfeito. Como é apenas uma condição necessária, mas não suficiente, ela pode ser usada para verificar se um dado triplo de números não é um triplo pitagórico ao falhar no teste. Por exemplo, os triplos {6, 12, 18} e {1, 8, 9} passam cada um no teste de que ( c - a ) ( c - b ) / 2 é um quadrado perfeito, mas nenhum é um triplo pitagórico.
- Quando um triplo de números de um , b e c forma uma primitiva de Pitágoras triplas, em seguida, ( c menos o mesmo pé) e um meio de ( c perna impar menos) são ambos quadrados perfeitos; no entanto, esta não é uma condição suficiente, pois os números {1, 8, 9} passam no teste dos quadrados perfeitos, mas não são um triplo pitagórico desde 1 2 + 8 2 ≠ 9 2 .
- No máximo um de a , b , c é um quadrado.
- A área de um triângulo pitagórico não pode ser o quadrado ou duas vezes o quadrado de um número natural.
- Exatamente um de a , b é divisível por 2 (é par ), mas nunca c .
- Exatamente um de a , b é divisível por 3, mas nunca c .
- Exatamente um de a , b é divisível por 4, mas nunca c (porque c nunca é par).
- Exatamente um de a , b , c é divisível por 5.
- O maior número que sempre divide abc é 60.
- Qualquer número ímpar de forma a 2 m 1 , onde m é um inteiro e m > 1 , pode ser a perna ímpar de uma primitiva de Pitágoras tripla [PPT]. Consulte a seção PPT quase isósceles abaixo. No entanto, apenas números pares divisíveis por 4 podem ser a perna par de um PPT. Isso ocorre porque a fórmula de Euclides para a perna par dada acima é 2 mn e uma de m ou n deve ser par.
- A hipotenusa c é a soma de dois quadrados. Isso requer que todos os seus fatores primos sejam primos na forma 4 n + 1 . Portanto, c tem a forma 4 n + 1 . Uma sequência de possíveis números de hipotenusa para um PPT pode ser encontrada em (sequência A008846 no OEIS ).
- A área ( K = ab / 2) é um número congruente divisível por 6.
- Em todo triângulo pitagórico, o raio do incircle e os raios dos três círculos são números naturais. Especificamente, para um triplo primitivo, o raio do incircle é r = n ( m - n ) , e os raios dos excírculos opostos aos lados m 2 - n 2 , 2mn , e a hipotenusa m 2 + n 2 são respectivamente m ( m - n ) , n ( m + n ) e m ( m + n ) .
- Como para qualquer triângulo retângulo, o inverso do teorema de Tales diz que o diâmetro do circuncírculo é igual à hipotenusa; portanto, para triplos primitivos, o circundiâmetro é m 2 + n 2 , e o circumradius é a metade disso e, portanto, é racional, mas não inteiro (uma vez que m e n têm paridade oposta).
- Quando a área de um triângulo pitagórico é multiplicada pelas curvaturas de seu incircle e 3 excírculos, o resultado são quatro inteiros positivos w > x > y > z , respectivamente. Inteiros - w , x , y , z satisfazem a Equação do Círculo de Descartes . De forma equivalente, o raio do círculo Soddy externo de qualquer triângulo retângulo é igual ao seu semiperímetro. O centro Soddy externo está localizado em D , onde ACBD é um retângulo, ACB é o triângulo retângulo e AB é sua hipotenusa.
- Apenas dois lados de um triplo pitagórico primitivo podem ser primos simultaneamente porque, pela fórmula de Euclides para gerar um triplo pitagórico primitivo, uma das pernas deve ser composta e uniforme. No entanto, apenas um lado pode ser um inteiro de potência perfeita porque se dois lados fossem inteiros de potências perfeitas com expoente igual, isso contradiria o fato de que não há soluções inteiras para a equação diofantina , com , e sendo coprime par.
- Não há triângulos pitagóricos em que a hipotenusa e uma perna sejam as pernas de outro triângulo pitagórico; esta é uma das formas equivalentes do teorema do triângulo retângulo de Fermat .
- Cada triângulo pitagórico primitivo tem uma razão de área, K , para semiperímetro quadrado , s , que é único para si mesmo e é dado por
- Nenhum triângulo pitagórico primitivo tem uma altitude inteira da hipotenusa; isto é, todo triângulo pitagórico primitivo é indecomponível.
- O conjunto de todos os triplos pitagóricos primitivos forma uma árvore ternária enraizada de maneira natural; veja Árvore dos triplos pitagóricos primitivos .
- Nenhum dos ângulos agudos de um triângulo pitagórico pode ser um número racional de graus . (Isso segue do teorema de Niven .)
Casos especiais
Além disso, a existência de triplos pitagóricos especiais com certas propriedades adicionais pode ser garantida:
- Todo inteiro maior que 2 que não seja congruente com 2 mod 4 (em outras palavras, todo inteiro maior que 2 que não seja da forma 4 k + 2 ) é parte de uma tripla pitagórica primitiva. (Se o inteiro tiver a forma 4 k , pode-se tomar n = 1 e m = 2 k na fórmula de Euclides; se o inteiro for 2 k + 1 , pode-se tomar n = k e m = k + 1. )
- Todo número inteiro maior que 2 faz parte de uma tripla pitagórica primitiva ou não primitiva. Por exemplo, os inteiros 6, 10, 14 e 18 não fazem parte dos triplos primitivos, mas fazem parte dos triplos não primitivos (6, 8, 10) , (14, 48, 50) e (18, 80, 82) .
- Existem infinitos triplos pitagóricos nos quais a hipotenusa e a perna mais longa diferem exatamente em um. Esses triplos são necessariamente primitivos e têm a forma (2 n + 1, 2 n 2 + 2 n , 2 n 2 + 2 n +1) . Isso resulta da fórmula de Euclides, observando que a condição implica que o triplo é primitivo e deve verificar ( m 2 + n 2 ) - 2 mn = 1 . Isso implica ( m - n ) 2 = 1 e, portanto, m = n + 1 . A forma anterior das triplas resulta, portanto, da substituição de m por n + 1 na fórmula de Euclides.
- Existem infinitos trios pitagóricos primitivos nos quais a hipotenusa e a perna mais longa diferem exatamente em dois. Eles são todos primitivos e são obtidos colocando n = 1 na fórmula de Euclides. De forma mais geral, para cada número inteiro k > 0, existem infinitos triplos pitagóricos primitivos nos quais a hipotenusa e a perna ímpar diferem em 2 k 2 . Eles são obtidos colocando n = k na fórmula de Euclides.
- Existem infinitos triplos pitagóricos nos quais as duas pernas diferem exatamente por uma. Por exemplo, 20 2 + 21 2 = 29 2 ; estes são gerados pela fórmula de Euclides quando é convergente para √ 2 .
- Para cada número natural k , existem k triplos pitagóricos com hipotenos diferentes e na mesma área.
- Para cada número natural k , existem pelo menos k triplos pitagóricos primitivos diferentes com a mesma perna a , onde a é algum número natural (o comprimento da perna par é 2 mn , e é suficiente escolher a com muitas fatorações, por exemplo a = 4 b , onde b é um produto de k diferentes primos ímpares; isso produz pelo menos 2 k triplos primitivos diferentes).
- Para cada número natural n , existem pelo menos n diferentes triplos pitagóricos com a mesma hipotenusa.
- Existem infinitos triplos pitagóricos com números quadrados para a hipotenusa c e a soma das pernas a + b . De acordo com Fermat, o menor desses triplos tem lados a = 4.565.486.027.761; b = 1.061.652.293.520; e c = 4.687.298.610.289. Aqui a + b = 2.372.159 2 e c = 2.165.017 2 . Isso é gerado pela fórmula de Euclides com valores de parâmetro m = 2.150.905 e n = 246.792.
- Existem triângulos pitagóricos não primitivos com altitude inteira da hipotenusa . Esses triângulos pitagóricos são conhecidos como decomponíveis, pois podem ser divididos ao longo desta altitude em dois triângulos pitagóricos menores.
Geometria da fórmula de Euclides
Pontos racionais em um círculo unitário

Fórmula de Euclides para um triplo pitagórico
pode ser entendido em termos da geometria de pontos racionais no círculo unitário ( Trautman 1998 ).
Na verdade, um ponto no plano cartesiano com coordenadas ( x , y ) pertence ao círculo unitário se x 2 + y 2 = 1 . O ponto é racional se x e y forem números racionais , ou seja, se houver inteiros coprime a , b , c tais que
Multiplicando ambos os membros por c 2 , pode-se ver que os pontos racionais no círculo estão em correspondência um a um com os triplos pitagóricos primitivos.
O círculo unitário também pode ser definido por uma equação paramétrica
A fórmula de Euclides para triplos pitagóricos significa que, exceto para (−1, 0) , um ponto no círculo é racional se e somente se o valor correspondente de t for um número racional.
Abordagem estereográfica

Há uma correspondência entre pontos no círculo unitário com coordenadas racionais e triplas pitagóricas primitivas. Neste ponto, as fórmulas de Euclides podem ser derivadas por métodos de trigonometria ou de forma equivalente, usando a projeção estereográfica .
Para a abordagem estereográfica, suponha que P ′ é um ponto no eixo x com coordenadas racionais
Então, pode ser mostrado pela álgebra básica que o ponto P tem coordenadas
Isso estabelece que cada ponto racional do eixo x vai para um ponto racional do círculo unitário. O inverso, que todo ponto racional do círculo unitário vem de tal ponto do eixo x , segue aplicando a projeção estereográfica inversa. Suponha-se que P ( x , y ) é um ponto do círculo unitário com x e y números racionais. Então o ponto P ′ obtido por projeção estereográfica no eixo x tem coordenadas
o que é racional.
Em termos de geometria algébrica , a variedade algébrica de pontos racionais no círculo unitário é birracional em relação à linha afim sobre os números racionais. O círculo unitário é então chamado de curva racional , e é este fato que permite uma parametrização explícita dos pontos (número racional) sobre ele por meio de funções racionais.
Triângulos pitagóricos em uma rede 2D
Um 2D estrutura é uma matriz regular de pontos isolados, onde se houver um ponto é escolhido como a origem cartesiano (0, 0), em seguida, todos os outros pontos são em ( x , y ) onde x e y gama mais de todos os inteiros positivos e negativos . Qualquer triângulo pitagórico com triplo ( a , b , c ) pode ser desenhado dentro de uma rede 2D com vértices nas coordenadas (0, 0), ( a , 0) e (0, b ). A contagem de pontos da rede estritamente dentro dos limites do triângulo é dada por para triplos pitagóricos primitivos, essa contagem da rede interna é A área (pelo teorema de Pick igual a um menos que a contagem da rede interna mais metade da contagem da rede limite) é igual .
A primeira ocorrência de duas triplas pitagóricas primitivas compartilhando a mesma área ocorre com triângulos com lados (20, 21, 29), (12, 35, 37) e área comum 210 (sequência A093536 no OEIS ). A primeira ocorrência de dois triplos pitagóricos primitivos que compartilham a mesma contagem de rede interna ocorre com (18108, 252685, 253333), (28077, 162964, 165365) e contagem de rede interna 2287674594 (sequência A225760 no OEIS ). Três triplos pitagóricos primitivos foram encontrados compartilhando a mesma área: (4485, 5852, 7373), (3059, 8580, 9109), (1380, 19019, 19069) com a área 13123110. Até agora, nenhum conjunto de três triplos pitagóricos primitivos tem foram encontrados compartilhando a mesma contagem de rede interna.
Enumeração de triplos pitagóricos primitivos
Pela fórmula de Euclides, todos os triplos pitagóricos primitivos podem ser gerados a partir de inteiros e com , ímpar e . Portanto, há um mapeamento de 1 para 1 de racionais (em termos mais baixos) para triplos pitagóricos primitivos onde está no intervalo e ímpar.
O mapeamento reverso de um triplo primitivo em um racional é obtido estudando as duas somas e . Uma dessas somas será um quadrado que pode ser igualado e a outra será duas vezes um quadrado que pode ser igualado . Então, é possível determinar o racional .
Para enumerar os triplos pitagóricos primitivos, o racional pode ser expresso como um par ordenado e mapeado para um inteiro usando uma função de emparelhamento, como a função de emparelhamento de Cantor . Um exemplo pode ser visto em (sequência A277557 no OEIS ). Isso começa
- e dá razões
- estes, por sua vez, geram triplas primitivas
Spinors e o grupo modular
Os triplos pitagóricos também podem ser codificados em uma matriz quadrada da forma
Uma matriz desta forma é simétrica . Além disso, o determinante de X é
que é zero precisamente quando ( a , b , c ) é um triplo pitagórico. Se X corresponder a uma tripla pitagórica, então, como uma matriz, ela deve ter classificação 1.
Uma vez que X é simétrico, segue-se de um resultado em álgebra linear que existe um vetor coluna ξ = [ m n ] T tal que o produto externo
-
( 1 )
mantém, onde o T denota a transposta da matriz . O vetor ξ é chamado de spinor (para o grupo de Lorentz SO (1, 2)). Em termos abstratos, a fórmula de Euclides significa que cada tripla primitiva pitagórica pode ser escrita como o produto externo com ela mesma de um espinor com entradas inteiras, como em ( 1 ).
O grupo modular Γ é o conjunto de matrizes 2 × 2 com entradas inteiras
com determinante igual a um: αδ - βγ = 1 . Este conjunto forma um grupo , já que o inverso de uma matriz em Γ está novamente em Γ, assim como o produto de duas matrizes em Γ. O grupo modular atua na coleção de todos os espinores inteiros. Além disso, o grupo é transitivo na coleção de espinores inteiros com entradas relativamente primos. Pois se [ m n ] T tem entradas relativamente primos, então
onde u e v são seleccionados (pelo algoritmo de Euclides ) de modo que os mu + nv = 1 .
Ao agir sobre o espinor ξ em ( 1 ), a ação de Γ passa a uma ação sobre os triplos pitagóricos, desde que sejam permitidos triplos com componentes possivelmente negativos. Assim, se A é uma matriz em Γ, então
-
( 2 )
dá origem a uma ação na matriz X em ( 1 ). Isso não dá uma ação bem definida em triplos primitivos, uma vez que pode transformar um triplo primitivo em um imprimitivo. É conveniente neste ponto (por Trautman 1998 ) chamar um padrão triplo ( a , b , c ) se c > 0 e ( a , b , c ) forem relativamente primos ou ( a / 2, b / 2, c / 2) são relativamente primos com um / 2 estranho. Se o spinor [ m n ] T tem entradas relativamente primos, então o triplo associado ( a , b , c ) determinado por ( 1 ) é um triplo padrão. Conclui-se que a ação do grupo modular é transitiva no conjunto de triplos padrão.
Alternativamente, restrinja a atenção aos valores de m e n para os quais m é ímpar e n é par. Seja o subgrupo Γ (2) de Γ o núcleo do homomorfismo de grupo
onde SL (2, Z 2 ) é o grupo linear especial sobre o corpo finito Z 2 do módulo 2 de inteiros . Então Γ (2) é o grupo de transformações unimodulares que preservam a paridade de cada entrada. Assim, se a primeira entrada de ξ é ímpar e a segunda entrada é par, então o mesmo é verdadeiro para A ξ para todo A ∈ Γ (2) . De fato, sob a ação ( 2 ), o grupo Γ (2) atua transitivamente na coleção de triplas pitagóricas primitivas ( Alperin 2005 ).
O grupo Γ (2) é o grupo livre cujos geradores são as matrizes
Consequentemente, cada primitiva de Pitágoras tripla pode ser obtido de uma forma única como um produto de cópias das matrizes L e L .
Relações pai / filho
Por um resultado de Berggren (1934) , todos os triplos pitagóricos primitivos podem ser gerados a partir do triângulo (3, 4, 5) usando as três transformações lineares T 1 , T 2 , T 3 abaixo, onde a , b , c são lados de um triplo:
| novo lado a | novo lado b | novo lado c | |
| T 1 : | a - 2 b + 2 c | 2 a - b + 2 c | 2 a - 2 b + 3 c |
| T 2 : | a + 2 b + 2 c | 2 a + b + 2 c | 2 a + 2 b + 3 c |
| T 3 : | - a + 2 b + 2 c | -2 a + b + 2 c | −2 a + 2 b + 3 c |
Em outras palavras, cada triplo primitivo será um "pai" de três triplos primitivos adicionais. Partindo do nó inicial com a = 3, b = 4 e c = 5, a operação T 1 produz o novo triplo
- (3 - (2 × 4) + (2 × 5), (2 × 3) - 4 + (2 × 5), (2 × 3) - (2 × 4) + (3 × 5)) = (5 , 12, 13),
e de modo semelhante T 2 e T 3 produzir os triplos (21, 20, 29) e (15, 8, 17).
As transformações lineares T 1 , T 2 e T 3 têm uma interpretação geométrica na linguagem das formas quadráticas . Eles estão intimamente relacionados (mas não são iguais a) reflexões que geram o grupo ortogonal de x 2 + y 2 - z 2 sobre os inteiros.
Relação com inteiros gaussianos
Alternativamente, as fórmulas de Euclides podem ser analisadas e comprovadas usando os inteiros gaussianos . Inteiros de Gauss são números complexos da forma α = u + VI , onde u e v são comuns inteiros e i é a raiz quadrada de um negativo . As unidades dos inteiros gaussianos são ± 1 e ± i. Os inteiros comuns são chamados de inteiros racionais e indicado como Z . Os inteiros gaussianos são denotados como Z [ i ]. O lado direito do teorema de Pitágoras pode ser fatorado em inteiros gaussianos:
A Pitágoras primitiva triplo é aquele em que a e b são primos entre si , ou seja, eles não compartilham fatores primos dos números inteiros. Para tal triplo, ou a ou b é par, e o outro é ímpar; a partir disso, segue-se que c também é ímpar.
Os dois fatores z : = a + bi e z * : = a - bi de uma tripla pitagórica primitiva, cada um é igual ao quadrado de um inteiro gaussiano. Isso pode ser provado usando a propriedade de que todo inteiro gaussiano pode ser fatorado exclusivamente em primos gaussianos até unidades . (Essa fatoração única decorre do fato de que, grosso modo, uma versão do algoritmo euclidiano pode ser definida neles.) A prova tem três etapas. Primeiro, se um e b compartilham fatores não privilegiada, no números inteiros, então eles também não compartilham fatores primos nas inteiros de Gauss. (Assume um = gu e b = GV com Gaussiana inteiros g , u e v e g não uma unidade. Em seguida, u e v encontram-se na mesma linha que passa pela origem. Inteiros Todos Gaussianas numa tal linha são múltiplos inteiros de um número inteiro de Gauss h . Mas então o inteiro gh ≠ ± 1 divide tanto a e b .) em segundo lugar, segue-se que z e z * da mesma forma não compartilham fatores primos nas inteiros de Gauss. Pois se o fizessem, então seu divisor comum δ também dividiria z + z * = 2 a e z - z * = 2 ib . Uma vez que um e b são primos entre si, o que implica que divide ô 2 = (1 + i) (1 - i) i = (1 - i) 2 . Da fórmula c 2 = zz * , isso por sua vez implicaria que c é par, ao contrário da hipótese de uma tripla pitagórica primitiva. Terceiro, como c 2 é um quadrado, todo primo gaussiano em sua fatoração é duplicado, ou seja, aparece um número par de vezes. Como z e z * não compartilham fatores primos, essa duplicação também é verdadeira para eles. Portanto, z e z * são quadrados.
Assim, o primeiro fator pode ser escrito
As partes real e imaginária desta equação fornecem as duas fórmulas:
Para qualquer tripla pitagórica primitiva, deve haver inteiros m e n de forma que essas duas equações sejam satisfeitas. Conseqüentemente, cada triplo pitagórico pode ser gerado a partir de alguma escolha desses inteiros.
Como inteiros Gaussianos quadrados perfeitos
Se considerarmos o quadrado de um inteiro gaussiano, obteremos a seguinte interpretação direta da fórmula de Euclides como representando o quadrado perfeito de um inteiro gaussiano.
Usando os fatos de que os inteiros gaussianos são um domínio euclidiano e que para um inteiro gaussiano p é sempre um quadrado, é possível mostrar que um triplo pitagórico corresponde ao quadrado de um inteiro gaussiano primo se a hipotenusa for primo.
Se o inteiro gaussiano não for primo, ele é o produto de dois inteiros gaussianos p e q com e inteiros. Como as magnitudes se multiplicam nos inteiros gaussianos, o produto deve ser , que quando elevado ao quadrado para encontrar uma tripla pitagórica deve ser composto. O contrapositivo completa a prova.
Relação com elipses com dimensões integrais
Com referência à figura e à definição dos focos de uma elipse , F 1 e F 2 , para qualquer ponto P na elipse, F 1 P + PF 2 é constante.
Como os pontos A e B estão ambos na elipse, F 1 A + AF 2 = F 1 B + BF 2 . Devido à simetria, F 1 A + AF 2 = F 2 A '+ AF 2 = AA' = 2 AC, e F 1 B + BF 2 = 2 BF 2 . Portanto, AC = BF 2 .
Assim, se BCF 2 é um triângulo retângulo com lados inteiros, a separação dos focos, excentricidade linear, eixo menor e eixo maior também são inteiros.
Distribuição de triplos
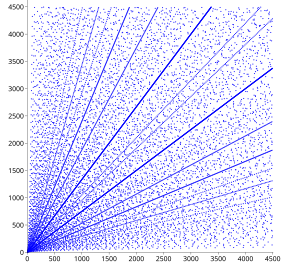
Existem vários resultados sobre a distribuição dos triplos pitagóricos. No gráfico de dispersão, vários padrões óbvios já são aparentes. Sempre que as pernas ( a , b ) de um triplo primitivo aparecem no gráfico, todos os múltiplos inteiros de ( a , b ) também devem aparecer no gráfico, e esta propriedade produz a aparência de linhas que irradiam da origem no diagrama.
Dentro da dispersão, existem conjuntos de padrões parabólicos com uma alta densidade de pontos e todos os seus focos na origem, abrindo-se nas quatro direções. Diferentes parábolas se cruzam nos eixos e parecem refletir fora do eixo com um ângulo de incidência de 45 graus, com uma terceira parábola entrando de forma perpendicular. Dentro desse quadrante, cada arco centrado na origem mostra aquela seção da parábola que se encontra entre sua ponta e sua intersecção com seu reto semilateral .
Esses padrões podem ser explicados da seguinte maneira. Se é um número inteiro, então ( a , , ) é uma tríplice de Pitágoras. (Na verdade, cada Pitágoras tripla ( uma , b , c ) pode ser escrita desta forma com número inteiro n , possivelmente depois de trocar de um e b , uma vez que e um e b não poderem ser ambos estranho.) O Pitágoras triplica assim encontram-se em curvas indicadas por , que é, parábolas reflectido pela um -axis, e as curvas correspondentes, com um e b intercambiadas. Se a for variado para um dado n (isto é, em uma dada parábola), valores inteiros de b ocorrem com relativa freqüência se n for um quadrado ou um pequeno múltiplo de um quadrado. Se vários desses valores estiverem próximos uns dos outros, as parábolas correspondentes coincidirão aproximadamente e as triplas se agruparão em uma estreita faixa parabólica. Por exemplo, 38 2 = 1444, 2 × 27 2 = 1458, 3 × 22 2 = 1452, 5 × 17 2 = 1445 e 10 × 12 2 = 1440; a faixa parabólica correspondente em torno de n ≈ 1450 é claramente visível no gráfico de dispersão.
As propriedades angulares descritas acima decorrem imediatamente da forma funcional das parábolas. As parábolas reflectem-se no uma -axis a um = 2 N , e o derivado de b com respeito a uma neste ponto é 1; portanto, o ângulo de incidência é de 45 °. Como os clusters, como todos os triplos, são repetidos em múltiplos inteiros, o valor 2 n também corresponde a um cluster. Os correspondentes intersecta a parábola b -axis em ângulos rectos em b = 2 N , e daí a sua reflexão sobre a transferência de um e b intersecta a um -axis em ângulos rectos em um = 2 n , precisamente onde a parábola para n se reflecte no a um -axis. (O mesmo é claro para a e b trocados.)
Albert Fässler e outros fornecem insights sobre a importância dessas parábolas no contexto de mapeamentos conformes.
A sequência platônica
O caso n = 1 da construção mais geral das triplas pitagóricas é conhecido há muito tempo. Proclus , em seu comentário à Proposição 47 do primeiro livro de Euclides Elements , descreve-o como segue:
Certos métodos para a descoberta de triângulos desse tipo são transmitidos, um deles se refere a Platão e outro a Pitágoras . (O último) começa com números ímpares. Pois isso torna o número ímpar o menor dos lados do ângulo reto; então toma o quadrado dele, subtrai a unidade e faz a metade da diferença o maior dos lados sobre o ângulo reto; por último, ele adiciona unidade a isso e assim forma o lado remanescente, a hipotenusa.
... Pois o método de Platão argumenta a partir de números pares. Ele pega o número par dado e o torna um dos lados do ângulo reto; então, dividindo esse número ao meio e elevando a metade ao quadrado, ele adiciona unidade ao quadrado para formar a hipotenusa e subtrai unidade do quadrado para formar o outro lado sobre o ângulo reto. ... Assim, formou o mesmo triângulo que foi obtido pelo outro método.
Na forma de equação, isso se torna:
a é ímpar (Pitágoras, c. 540 aC):
a é par (Platão, c. 380 aC):
Pode ser demonstrado que todos os triplos de Pitágoras pode ser obtido, com redimensionamento apropriado, a partir da sequência platônica básico ( um , ( uma 2 - 1) / 2 e ( uma 2 + 1) / 2 ), permitindo que um tomar não inteiro valores racionais. Se a for substituído pela fração m / n na sequência, o resultado será igual ao gerador triplo 'padrão' (2 mn , m 2 - n 2 , m 2 + n 2 ) após o reescalonamento. Daqui resulta que cada tripla tem uma racional correspondendo um valor que pode ser utilizado para gerar um semelhante triângulo (um com os mesmos ângulos e com três lados nas mesmas proporções que as originais). Por exemplo, o equivalente platônico de (56, 33, 65) é gerado por a = m / n = 7/4 como ( a , ( a 2 –1) / 2, ( a 2 +1) / 2) = ( 56/32, 33/32, 65/32). A própria sequência platônica pode ser derivada seguindo as etapas para 'dividir o quadrado' descrito em Diophantus II.VIII .
A equação de Jacobi-Madden
A equação,
é equivalente ao triplo pitagórico especial,
Há um número infinito de soluções para essa equação, já que resolver as variáveis envolve uma curva elíptica . Os pequenos são,
Somas iguais de dois quadrados
Uma maneira de gerar soluções para é parametrizar a, b, c, d em termos de inteiros m, n, p, q da seguinte forma:
Somas iguais de dois quartos poderes
Dados dois conjuntos de triplos pitagóricos,
o problema de encontrar produtos iguais de um lado não hipotenusa e da hipotenusa,
é facilmente visto como equivalente à equação,
e foi resolvido pela primeira vez por Euler como . Como ele mostrou que este é um ponto racional em uma curva elíptica , então há um número infinito de soluções. Na verdade, ele também encontrou uma parametrização polinomial de 7º grau.
Teorema do Círculo de Descartes
Para o caso do teorema do círculo de Descartes, onde todas as variáveis são quadrados,
Euler mostrou que isso é equivalente a três triplos pitagóricos simultâneos,
Há também um número infinito de soluções, e para o caso especial quando , então, a equação simplifica para,
com pequenas soluções e pode ser resolvido como formas quadráticas binárias .
Triplos pitagóricos quase isósceles
Nenhuma tripla pitagórica é isósceles , porque a razão da hipotenusa para qualquer outro lado é √ 2 , mas √ 2 não pode ser expressa como a razão de 2 inteiros .
Existem, no entanto, triângulos retângulos com lados inteiros para os quais os comprimentos dos lados não hipotenusa diferem por um, como,
e um número infinito de outros. Eles podem ser completamente parametrizados como,
onde { x, y } são as soluções para a equação de Pell .
Se a , b , c são os lados deste tipo de triplo pitagórico primitivo (PPT), então a solução para a equação de Pell é dada pela fórmula recursiva
- com e
- com e
- com e .
Esta sequência de PPTs forma a haste central (tronco) da árvore ternária enraizada de PPTs.
Quando é o lado não hipotenusa mais longo e a hipotenusa que diferem em um, como em
então a solução completa para o PPT a , b , c é
e
onde inteiro é o parâmetro gerador.
Mostra que todos os números ímpares (maiores que 1) aparecem neste tipo de PPT quase isósceles. Esta sequência de PPTs forma o caule externo do lado direito da árvore ternária enraizada de PPTs.
Outra propriedade deste tipo de PPT quase isósceles é que os lados estão relacionados de tal forma que
para algum número inteiro . Ou em outras palavras, é divisível por , como em
- .
Números de Fibonacci em triplos pitagóricos
A partir de 5, cada segundo número de Fibonacci é o comprimento da hipotenusa de um triângulo retângulo com lados inteiros, ou seja, o maior número em um triplo pitagórico, obtido a partir da fórmula
- (3,4,5), (5,12,13), (16,30,34), (39,80,89), ...
O lado do meio de cada um desses triângulos é a soma dos três lados do triângulo anterior.
Generalizações
Existem várias maneiras de generalizar o conceito de triplos pitagóricos.
Pitagórico n- duplo
Usando a identidade algébrica simples ,
para x 0 , x 1 arbitrário , é fácil provar que o quadrado da soma de n quadrados é ele mesmo a soma de n quadrados, deixando x 0 = x 2 2 + x 3 2 + ... + x n 2 e em seguida, distribuindo os termos. Pode-se ver como triplos e quádruplos Pitágoras são apenas os casos particulares x 0 = x 2 2 e x 0 = x 2 2 + x 3 2 , respectivamente, e assim por diante para a outra n , com quíntuplos dadas pela
Uma vez que a soma F ( k , m ) de k quadrados consecutivos começando com m 2 é dada pela fórmula,
pode-se encontrar valores ( k , m ) para que F ( k , m ) seja um quadrado, como um de Hirschhorn onde o número de termos é ele mesmo um quadrado,
e v ≥ 5 é qualquer número inteiro não divisível por 2 ou 3. Para o menor caso v = 5, por conseguinte, k = 25, este rendimento do problema de empilhamento potente bem conhecido de Lucas ,
um fato que está conectado à rede Leech .
Além disso, se em um pitagórico n- duplo ( n ≥ 4) todos os adendos são consecutivos, exceto um, pode-se usar a equação,
Uma vez que a segunda potência de p se cancela, isso é apenas linear e facilmente resolvido como se k , m devesse ser escolhido de forma que p seja um inteiro, com um pequeno exemplo sendo k = 5, m = 1 resultando,
Assim, uma maneira de gerar n- duplas pitagóricas é usar, para vários x ,
onde q = n –2 e onde
Quádruplo pitagórico
Um conjunto de quatro inteiros positivos a , b , c e d tais que a 2 + b 2 + c 2 = d 2 é chamado de quádruplo pitagórico . O exemplo mais simples é (1, 2, 2, 3), uma vez que 1 2 + 2 2 + 2 2 = 3 2 . O próximo exemplo mais simples (primitivo) é (2, 3, 6, 7), uma vez que 2 2 + 3 2 + 6 2 = 7 2 .
Todos os quádruplos são dados pela fórmula
Último Teorema de Fermat
Uma generalização do conceito de triplos pitagóricos é a busca por triplos de inteiros positivos a , b e c , de modo que a n + b n = c n , para algum n estritamente maior que 2. Pierre de Fermat em 1637 afirmou que não esse triplo existe, uma afirmação que veio a ser conhecida como o último teorema de Fermat porque demorou mais do que qualquer outra conjectura de Fermat para ser provada ou refutada. A primeira prova foi dada por Andrew Wiles em 1994.
n - 1 ou n n º poderes soma a um n º de energia
Outra generalização está à procura de sequências de n + 1 inteiros positivos para o qual o n º poder do passado é a soma dos n º poderes dos termos anteriores. As menores sequências para valores conhecidos de n são:
- n = 3: {3, 4, 5; 6}.
- n = 4: {30, 120, 272, 315; 353}
- n = 5: {19, 43, 46, 47, 67; 72}
- n = 7: {127, 258, 266, 413, 430, 439, 525; 568}
- n = 8: {90, 223, 478, 524, 748, 1088, 1190, 1324; 1409}
Para o caso n = 3, no qual é denominado cúbico de Fermat , existe uma fórmula geral que fornece todas as soluções.
Uma generalização ligeiramente diferente permite que a soma de ( k + 1) n- ésimas potências seja igual à soma de ( n - k ) n- ésimas potências. Por exemplo:
- ( n = 3): 1 3 + 12 3 = 9 3 + 10 3 , que ficou famoso pela lembrança de Hardy de uma conversa com Ramanujan sobre o número 1729 ser o menor número que pode ser expresso como a soma de dois cubos de duas maneiras distintas .
Há também podem existir n - 1 inteiros positivos cujo n º poderes soma a um n º de energia (embora, por último teorema de Fermat , não para n = 3); esses são contra-exemplos à conjectura da soma dos poderes de Euler . Os menores contra-exemplos conhecidos são
- n = 4: (95800, 217519, 414560; 422481)
- n = 5: (27, 84, 110, 133; 144)
Triângulo heroniano triplica
Um triângulo heroniano é comumente definido como um com lados inteiros cuja área também é um inteiro, e devemos considerar os triângulos heronianos com lados inteiros distintos . Os comprimentos dos lados de tal triângulo formam um triplo Heronian ( a, b, c ) fornecido a < b < c . Cada triplo pitagórico é um triplo heroniano, porque pelo menos uma das pernas a , b deve ser par em um triplo pitagórico, então a área ab / 2 é um número inteiro. No entanto, nem todo triplo heroniano é um triplo pitagórico, como mostra o exemplo (4, 13, 15) com a área 24.
Se ( a , b , c ) é um triplo heroniano, então é ( ma , mb , mc ) onde m é qualquer inteiro positivo; sua área será o inteiro que é m 2 vezes a área inteira do triângulo ( a , b , c ) . O triplo heroniano ( a , b , c ) é primitivo, desde que a , b , c sejam coprimos setwise . (Com os triplos pitagóricos primitivos, a afirmação mais forte de que eles são coprimes em pares também se aplica, mas com os triângulos heronianos primitivos a afirmação mais forte nem sempre é verdadeira, como com (7, 15, 20) .) Aqui estão alguns dos primitivos mais simples Triplos heronianos que não são triplos pitagóricos:
- (4, 13, 15) com área 24
- (3, 25, 26) com área 36
- (7, 15, 20) com área 42
- (6, 25, 29) com área 60
- (11, 13, 20) com área 66
- (13, 14, 15) com área 84
- (13, 20, 21) com área 126
Pela fórmula de Heron , a condição extra para um triplo de inteiros positivos ( a , b , c ) com a < b < c sendo Heroniano é que
- ( a 2 + b 2 + c 2 ) 2 - 2 ( a 4 + b 4 + c 4 )
ou equivalente
- 2 ( a 2 b 2 + a 2 c 2 + b 2 c 2 ) - ( a 4 + b 4 + c 4 )
ser um quadrado perfeito diferente de zero divisível por 16.
Aplicativo para criptografia
Os triplos pitagóricos primitivos têm sido usados na criptografia como sequências aleatórias e para a geração de chaves.
Veja também
- Problema dos triplos booleanos pitagóricos
- Congruum
- Diophantus II.VIII
- Eisenstein triplo
- Tijolo de Euler
- Triângulo heroniano
- Teorema de Hilbert 90
- Triângulo inteiro
- Aritmética modular
- Número não hipotenusa
- Plimpton 322
- Pitagórico
- Quádruplo pitagórico
- Fórmula de meio-ângulo tangente
- Identidade trigonométrica
Notas
Referências
- Alperin, Roger C. (2005), "The modular tree of Pythagoras" (PDF) , American Mathematical Monthly , 112 (9): 807–816, CiteSeerX 10.1.1.112.3085 , doi : 10.2307 / 30037602 , JSTOR 30037602 , MR 2179860
- Berggren, B. (1934), "Pytagoreiska trianglar", Tidskrift för Elementär Matematik, Fysik och Kemi (em sueco), 17 : 129-139
- Barning, FJM (1963), "Over pythagorese en bijna-pythagorese driehoeken en een generatieproces met behulp van unimodulaire matrices" (PDF) , Math. Centrum Amsterdam Afd. Zuivere Wisk. (em holandês), ZW-011: 37
- Eckert, Ernest (1992), "Primitive Pythagorean triples", The College Mathematics Journal , 23 (5): 413-417, doi : 10.2307 / 2686417 , JSTOR 2686417
- Elkies, Noam , triplos pitagóricos e teorema de Hilbert 90 (PDF)
- Heath, Thomas (1956), The Thirteen Books of Euclid's Elements vol. 1 (Livros I e II) (2ª ed.), Dover Publications, ISBN 978-0-486-60088-8
- Long, Calvin T. (1972), Elementary Introduction to Number Theory (2ª ed.), Lexington: DC Heath and Company , LCCN 77171950
- Martin, Artemas (1875), "Rational retângulo triângulos quase isósceles", The Analyst , 3 (2): 47-50, doi : 10.2307 / 2635906 , JSTOR 2635906
- McCullough, Darryl (2005), "Height and excess of Pythagorean triples" (PDF) , Mathematics Magazine , 78 (1): 26–44, doi : 10.1080 / 0025570X.2005.11953298 , S2CID 1701449
- Romik, Dan (2008), "The dynamics of Pythagorean triples" (PDF) , Trans. Amer. Matemática. Soc. , 360 (11): 6045–6064, arXiv : math.DS / 0406512 , doi : 10.1090 / S0002-9947-08-04467-X , MR 2425702
- Teigen, MG; Hadwin, DW (1971), "On Generating Pythagorean Triples", The American Mathematical Monthly , 78 (4): 378-379, doi : 10.2307 / 2316903 , JSTOR 2316903
- Trautman, Andrzej (1998), "Pythagorean spinors and Penrose twistors" , em SA Hugget; LJ Mason; KP Tod; ST Tsou; NMJ Woodhouse (eds.), Universo geométrico (PostScript)
links externos
- Álgebras de Clifford e parametrização de Euclides de triplos pitagóricos
- Curiosas consequências de um quadrático miscopiado
- Discussão das propriedades dos triplos pitagóricos, calculadoras interativas, quebra-cabeças e problemas
- Gerando triplas pitagóricas usando progressões aritméticas
- "Pythagorean numbers" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
- Calculadora interativa para triplos pitagóricos
- A equação de Pell negativa e os triplos pitagóricos
- Parametrização de triplos pitagóricos por um único triplo de polinômios
- Price, H. Lee (2008), "The Pythagorean Tree: A New Species", arXiv : 0809.4324 [ math.HO ]
- Triplo Pitagórico e o Círculo de Unidade , cap. 2-3, em " A Friendly Introduction to Number Theory " por Joseph H. Silverman, 3ª ed., 2006, Pearson Prentice Hall, Upper Saddle River, NJ, ISBN 0-13-186137-9
- Triplos pitagóricos em um miniaplicativo interativo que mostra as relações do círculo unitário com os triplos pitagóricos
- Trigêmeos pitagóricos
- O notável círculo de um triângulo
- Soluções para pares quadráticos compatíveis em relação aos triplos pitagóricos
- Propriedades teóricas dos triplos pitagóricos e conexões com a geometria
- A (s) árvore (s) trinária (s) subjacente (s) aos triplos pitagóricos primitivos no corte do nó
- Weisstein, Eric W. "Pythagorean Triple" . MathWorld .

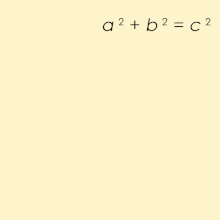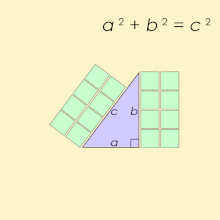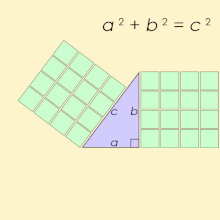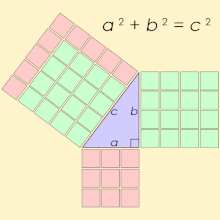



























































![X = 2 {\ begin {bmatrix} m \\ n \ end {bmatrix}} [m \ n] = 2 \ xi \ xi ^ {T} \,](https://wikimedia.org/api/rest_v1/media/math/render/svg/248a4dd30e8590ddf33a9f53d452656dff6711ec)









































































