Porta lógica quântica - Quantum logic gate

Na computação quântica e, especificamente, no modelo de circuito quântico de computação , uma porta lógica quântica (ou simplesmente porta quântica ) é um circuito quântico básico operando em um pequeno número de qubits . Eles são os blocos de construção dos circuitos quânticos, como as portas lógicas clássicas são para os circuitos digitais convencionais.

Ao contrário de muitas portas lógicas clássicas, as portas lógicas quânticas são reversíveis . No entanto, é possível realizar computação clássica usando apenas portas reversíveis. Por exemplo, a porta Toffoli reversível pode implementar todas as funções booleanas, geralmente ao custo de ter que usar bits ancilla . A porta de Toffoli tem um equivalente quântico direto, mostrando que os circuitos quânticos podem realizar todas as operações realizadas por circuitos clássicos.

Portas quânticas são operadores unitários e são descritos como matrizes unitárias em relação a alguma base . Normalmente usamos a base computacional , que a menos que a comparemos com algo, significa apenas que para um sistema quântico de nível d (como um qubit , um registrador quântico ou qutrits e qudits ) rotulamos os vetores de base ortogonal , ou usamos notação binária . ${\ displaystyle | 0 \ rangle, | 1 \ rangle, \ dots, | d-1 \ rangle}$

Portas lógicas quânticas comuns por nome (incluindo abreviação), forma (s) de circuito e as matrizes unitárias correspondentes.

História

Um somador quântico completo , fornecido por Feynman em 1986. Consiste apenas nas portas Toffoli e CNOT . A porta que está rodeada pelo quadrado pontilhado nesta imagem pode ser omitida se a descomputação para restaurar a saída B não for necessária.

A notação atual para portas quânticas foi desenvolvida por muitos dos fundadores da ciência da informação quântica, incluindo Adriano Barenco, Charles Bennett , Richard Cleve , David P. DiVincenzo , Norman Margolus , Peter Shor , Tycho Sleator , John A. Smolin e Harald Weinfurter, com base na notação introduzida por Richard Feynman .

Representação

Os estados de qubit simples que não são emaranhados e não têm fase global podem ser representados como pontos na superfície da esfera de Bloch , escritos como Rotações sobre os eixos

x, y, z

da esfera de Bloch são representados pelas portas do operador de rotação .

{\ displaystyle | \ psi \ rangle = \ cos \ left (\ theta / 2 \ right) | 0 \ rangle + e ^ {i \ varphi} \ sin \ left (\ theta / 2 \ right) | 1 \ rangle. }

As portas lógicas quânticas são representadas por matrizes unitárias . Uma porta que atua sobre qubits é representada por uma matriz unitária, e o conjunto de todas essas portas com a operação de grupo de multiplicação de matrizes é o grupo de simetria U (2 ⁿ ) . O quantum afirma que as portas atuam são vetores unitários em dimensões complexas , onde a norma é o módulo ao quadrado. Os vetores básicos (às vezes chamados de estados próprios ) são os resultados possíveis, se medidos , e um estado quântico é uma combinação linear desses resultados. As portas quânticas mais comuns operam em espaços vetoriais de um ou dois qubits, assim como as portas lógicas clássicas comuns operam em um ou dois bits . ${\ displaystyle n}$ ${\ displaystyle 2 ^ {n} \ vezes 2 ^ {n}}$ ${\ displaystyle 2 ^ {n}}$

Mesmo que as portas lógicas quânticas pertençam a um grupo de simetria contínua, o hardware real é inexato e, portanto, limitado em precisão. A aplicação de portas normalmente introduz erros, e a fidelidade dos estados quânticos diminui com o tempo. Se a correção de erros for usada, as portas utilizáveis serão ainda mais restritas a um conjunto finito. Posteriormente neste artigo, isso às vezes é ignorado, pois o foco está nas propriedades matemáticas das portas quânticas.

Os estados quânticos são normalmente representados por "kets", de uma notação conhecida como bra-ket .

A representação vetorial de um único qubit é:

{\ displaystyle | a \ rangle = v_ {0} | 0 \ rangle + v_ {1} | 1 \ rangle \ rightarrow {\ begin {bmatrix} v_ {0} \\ v_ {1} \ end {bmatrix}}, }

Aqui, e estão as amplitudes de probabilidade complexas do qubit. Esses valores determinam a probabilidade de medir 0 ou 1, ao medir o estado do qubit. Consulte a medição abaixo para obter detalhes. ${\ displaystyle v_ {0}}$ ${\ displaystyle v_ {1}}$

O valor zero é representado pelo cet , e o valor um é representado pelo cet . ${\ displaystyle | 0 \ rangle = {\ begin {bmatrix} 1 \\ 0 \ end {bmatrix}}}$ ${\ displaystyle | 1 \ rangle = {\ begin {bmatrix} 0 \\ 1 \ end {bmatrix}}}$

O produto tensorial (ou produto Kronecker ) é usado para combinar estados quânticos. O estado combinado de dois qubits é o produto tensorial dos dois qubits. O produto tensorial é denotado pelo símbolo . ${\ displaystyle \ otimes}$

A representação vetorial de dois qubits é:

{\ displaystyle | ab \ rangle = | a \ rangle \ otimes | b \ rangle = v_ {00} | 00 \ rangle + v_ {01} | 01 \ rangle + v_ {10} | 10 \ rangle + v_ {11} | 11 \ rangle \ rightarrow {\ begin {bmatrix} v_ {00} \\ v_ {01} \\ v_ {10} \\ v_ {11} \ end {bmatrix}},}

A ação da porta em um estado quântico específico é encontrada multiplicando o vetor que representa o estado, pela matriz que representa a porta. O resultado é um novo estado quântico : ${\ displaystyle | \ psi _ {1} \ rangle}$ ${\ displaystyle U}$ ${\ displaystyle | \ psi _ {2} \ rangle}$

{\ displaystyle U | \ psi _ {1} \ rangle = | \ psi _ {2} \ rangle.}

Exemplos notáveis

Existe um número infinito de portas. Alguns deles foram nomeados por vários autores, e a seguir seguem alguns dos mais usados na literatura.

Portão de identidade

A porta de identidade é a matriz de identidade , geralmente escrita como I , e é definida para um único qubit como

{\ displaystyle I = {\ begin {bmatrix} 1 e 0 \\ 0 & 1 \ end {bmatrix}},}

onde I é independente da base e não modifica o estado quântico. A porta de identidade é mais útil ao descrever matematicamente o resultado de várias operações de porta ou ao discutir circuitos multi-qubit.

Portões Pauli ( X , Y , Z )

As portas Pauli são as três matrizes Pauli e atuam em um único qubit. O Pauli X , Y e Z equivalem, respectivamente, a uma rotação em torno dos eixos x , y e z da esfera de Bloch em radianos. ${\ displaystyle (X, Y, Z)}$ ${\ displaystyle (\ sigma _ {x}, \ sigma _ {y}, \ sigma _ {z})}$ ${\ displaystyle \ pi}$

O Pauli- X portão é o equivalente quântico da porta NÃO para computadores clássicos com relação à base-padrão , , que distingue o z -axis na esfera de Bloch . Às vezes é chamado de bit-flip, pois mapeia para e para . Da mesma forma, o Pauli- Y mapeia para e para . Pauli Z deixa o estado de base inalterado e mapeia para . Devido a essa natureza, às vezes é chamado de inversão de fase. ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle i | 1 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle -i | 0 \ rangle}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle - | 1 \ rangle}$

Essas matrizes são geralmente representadas como

{\ displaystyle X = \ sigma _ {x} = \ operatorname {NOT} = {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix}},}

{\ displaystyle Y = \ sigma _ {y} = {\ begin {bmatrix} 0 & -i \\ i & 0 \ end {bmatrix}},}

{\ displaystyle Z = \ sigma _ {z} = {\ begin {bmatrix} 1 & 0 \\ 0 & -1 \ end {bmatrix}}.}

As matrizes de Pauli são involutórias , o que significa que o quadrado de uma matriz de Pauli é a matriz identidade .

{\ displaystyle I ^ {2} = X ^ {2} = Y ^ {2} = Z ^ {2} = - iXYZ = I}

As matrizes de Pauli também anti-comutação , por exemplo . ${\ displaystyle ZX = iY = -XZ}$

Raiz quadrada de NOT gate ( √ NOT )

Diagrama de circuito quântico de uma porta de raiz quadrada de NOT

A raiz quadrada de porta NOT (ou raiz quadrada de Pauli- X , ) atua em um único qubit. Ele mapeia o estado básico para e para . Na forma de matriz, é dado por ${\ displaystyle {\ sqrt {X}}}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle {\ frac {(1 + i) | 0 \ rangle + (1-i) | 1 \ rangle} {2}}}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle {\ frac {(1-i) | 0 \ rangle + (1 + i) | 1 \ rangle} {2}}}$

{\ displaystyle {\ sqrt {X}} = {\ sqrt {\ text {NOT}}} = {\ frac {1} {2}} {\ begin {bmatrix} 1 + i & 1-i \\ 1-i & 1 + i \ end {bmatrix}} = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} e ^ {i \ pi / 4} & e ^ {- i \ pi / 4} \\ e ^ {- i \ pi / 4} e e ^ {i \ pi / 4} \ end {bmatrix}}}

,

de tal modo que

{\ displaystyle ({\ sqrt {X}}) ^ {2} = \ left ({\ sqrt {\ text {NOT}}} \ right) ^ {2} = {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ fim {bmatrix}} = X.}

Esta operação representa uma rotação de $π / 2 em$ torno do eixo x na esfera de Bloch.

Portões controlados

Diagrama de circuito de portas controladas Pauli (da esquerda para a direita): CNOT (ou controlada X ), controlada Y e controlada Z .

As portas controladas atuam em 2 ou mais qubits, onde um ou mais qubits atuam como um controle para alguma operação. Por exemplo, a porta NOT controlada (ou CNOT ou CX) atua em 2 qubits e realiza a operação NOT no segundo qubit apenas quando o primeiro qubit é , e de outra forma o deixa inalterado. Com relação à base , , , , ela é representada pela matriz: ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 00 \ rangle}$ ${\ displaystyle | 01 \ rangle}$ ${\ displaystyle | 10 \ rangle}$ ${\ displaystyle | 11 \ rangle}$

{\ displaystyle {\ mbox {CNOT}} = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \ end {bmatrix}}.}

A porta CNOT (ou Pauli- X controlada ) pode ser descrita como a porta que mapeia os estados de base , onde é XOR . ${\ displaystyle | a, b \ rangle \ mapsto | a, a \ oplus b \ rangle}$ ${\ displaystyle \ oplus}$

Mais geralmente, se U for uma porta que opera em um único qubit com representação de matriz

{\ displaystyle U = {\ begin {bmatrix} u_ {00} & u_ {01} \\ u_ {10} & u_ {11} \ end {bmatrix}},}

então, a porta U controlada é uma porta que opera em dois qubits de tal forma que o primeiro qubit serve como um controle. Ele mapeia os estados básicos da seguinte maneira.

Representação do circuito da porta U controlada

{\ displaystyle | 00 \ rangle \ mapsto | 00 \ rangle}

{\ displaystyle | 01 \ rangle \ mapsto | 01 \ rangle}

{\ displaystyle | 10 \ rangle \ mapsto | 1 \ rangle \ otimes U | 0 \ rangle = | 1 \ rangle \ otimes (u_ {00} | 0 \ rangle + u_ {10} | 1 \ rangle)}

{\ displaystyle | 11 \ rangle \ mapsto | 1 \ rangle \ otimes U | 1 \ rangle = | 1 \ rangle \ otimes (u_ {01} | 0 \ rangle + u_ {11} | 1 \ rangle)}

A matriz que representa o U controlado é

{\ displaystyle {\ mbox {C}} U = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & u_ {00} & u_ {01} \\ 0 & 0 & u_ {10} & u_ {11} \ end {bmatrix}}.}

Quando U é um dos operadores Pauli, X , Y , Z , os respectivos termos "controlado- X ", "controlado- Y " ou "controlado- Z " são algumas vezes usados. Por vezes, esta é encurtado para apenas C X , C Y e C Z .

O controle pode ser estendido para portas com número arbitrário de qubits e funções em linguagens de programação.

Uma função controlada ou porta se comporta de maneira conceitualmente diferente, dependendo se alguém a aborda antes da medição ou após a medição : da perspectiva de antes da medição , a função controlada é executada simultaneamente em todos os estados básicos , de uma superposição ( combinação linear ) de resultados possíveis , que correspondem aos controles. Se, em vez disso, for abordado da perspectiva de após a medição , a função controlada foi executada ou não, dependendo de qual estado básico foi medido.

Portões de mudança de fase

A mudança de fase é uma família de portas de um qubit que mapeiam os estados básicos e . A probabilidade de medir a ou permanece inalterada após a aplicação desta porta, no entanto, ela modifica a fase do estado quântico. Isso é equivalente a traçar um círculo horizontal (uma linha de latitude) na esfera de Bloch por radianos. A porta de mudança de fase é representada pela matriz: ${\ displaystyle | 0 \ rangle \ mapsto | 0 \ rangle}$ ${\ displaystyle | 1 \ rangle \ mapsto e ^ {i \ varphi} | 1 \ rangle}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle \ varphi}$

{\ displaystyle P (\ varphi) = {\ begin {bmatrix} 1 & 0 \\ 0 & e ^ {i \ varphi} \ end {bmatrix}}}

onde é a mudança de fase com o período $2π$ . Alguns exemplos comuns são a porta T onde , a porta de fase (escrita S , embora S às vezes seja usado para portas SWAP) onde e a porta Pauli- Z onde . ${\ displaystyle \ varphi}$ ${\ textstyle \ varphi = {\ frac {\ pi} {4}}}$ ${\ textstyle \ varphi = {\ frac {\ pi} {2}}}$ ${\ displaystyle \ varphi = \ pi}$

As portas de mudança de fase estão relacionadas entre si da seguinte forma:

{\ displaystyle Z = {\ begin {bmatrix} 1 & 0 \\ 0 & e ^ {i \ pi} \ end {bmatrix}} = {\ begin {bmatrix} 1 & 0 \\ 0 & -1 \ end {bmatrix}} = P \ left (\ pi \ right)}

{\ displaystyle S = {\ begin {bmatrix} 1 & 0 \\ 0 & e ^ {i {\ frac {\ pi} {2}}} \ end {bmatrix}} = {\ begin {bmatrix} 1 & 0 \\ 0 & i \ end { bmatrix}} = P \ left ({\ frac {\ pi} {2}} \ right) = {\ sqrt {Z}}}

{\ displaystyle T = {\ begin {bmatrix} 1 & 0 \\ 0 & e ^ {i {\ frac {\ pi} {4}}} \ end {bmatrix}} = P \ left ({\ frac {\ pi} {4 }} \ right) = {\ sqrt {S}} = {\ sqrt [{4}] {Z}}}

{\ displaystyle P \ left ({\ frac {\ pi} {\ xi}} \ right) = {\ sqrt [{\ xi}] {Z}}}

para todos os reais, exceto 0

{\ displaystyle \ xi}

O argumento para a porta de deslocamento de fase está em U (1) , e a porta executa uma rotação de fase em U (1) ao longo do estado básico especificado (por exemplo, gira a fase em torno ) . U (1) é um subgrupo de U (n) e contém a fase do sistema quântico. Estendendo a uma rotação sobre uma fase genérica de ambos os estados da base de um sistema quântico de nível 2 (a qubit ) pode ser feito com um circuito em série : . Quando esta porta é a porta do operador de rotação . ${\ displaystyle P (\ varphi)}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle P (\ varphi)}$ ${\ displaystyle P (\ beta) \ cdot X \ cdot P (\ alpha) \ cdot X = {\ begin {bmatrix} e ^ {i \ alpha} & 0 \\ 0 & e ^ {i \ beta} \ end {bmatrix} }}$ ${\ displaystyle \ alpha = - \ beta}$ ${\ displaystyle R_ {z} (2 \ beta)}$

Apresentando o portal de fase global , também temos a identidade . ${\ displaystyle \ operatorname {Ph} (\ delta) = {\ begin {bmatrix} e ^ {i \ delta} & 0 \\ 0 & e ^ {i \ delta} \ end {bmatrix}} = \ left (P (\ delta ) \ cdot X \ direita) ^ {2} = e ^ {i \ delta} I}$ ${\ displaystyle R_ {z} (- \ gamma) \ operatorname {Ph} \ left ({\ frac {\ gamma} {2}} \ right) = P (\ gamma)}$

Portas de mudança de fase arbitrárias de qubit único estão disponíveis nativamente para processadores quânticos transmon por meio de temporização de pulsos de controle de microondas. Isso pode ser explicado em termos de mudança de quadro . ${\ displaystyle P (\ varphi)}$

Mudança de fase controlada

A porta de deslocamento de fase controlada de 2 qubit é:

{\ displaystyle \ mathrm {CPHASE} (\ varphi) = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & e ^ {i \ varphi} \ end {bmatrix}}}

Com relação à base computacional, muda de fase somente se atua sobre o estado : ${\ displaystyle \ varphi}$ ${\ displaystyle | 11 \ rangle}$

{\ displaystyle | a, b \ rangle \ mapsto {\ begin {cases} | a, e ^ {i \ varphi} b \ rangle & {\ mbox {for}} a = b = 1 \\ | a, b \ rangle & {\ mbox {caso contrário.}} \ end {cases}}}

A porta CZ é o caso especial onde . ${\ displaystyle \ varphi = \ pi}$

Portões do operador de rotação

O operador de rotação gates e são as matrizes de rotação analógicas em três eixos cartesianos de SO (3) , os eixos na projeção da esfera de Bloch : ${\ displaystyle R_ {x} (\ theta), R_ {y} (\ theta)}$ ${\ displaystyle R_ {z} (\ theta)}$

{\ displaystyle R_ {x} (\ theta) = \ exp (-iX \ theta / 2) = {\ begin {bmatrix} \ cos (\ theta / 2) & - i \ sin (\ theta / 2) \\ -i \ sin (\ theta / 2) & \ cos (\ theta / 2) \ end {bmatrix}},}

{\ displaystyle R_ {y} (\ theta) = \ exp (-iY \ theta / 2) = {\ begin {bmatrix} \ cos (\ theta / 2) & - \ sin (\ theta / 2) \\\ sin (\ theta / 2) & \ cos (\ theta / 2) \ end {bmatrix}},}

{\ displaystyle R_ {z} (\ theta) = \ exp (-iZ \ theta / 2) = {\ begin {bmatrix} \ exp (-i \ theta / 2) & 0 \\ 0 & \ exp (i \ theta / 2) \ end {bmatrix}}.}

Como as matrizes de Pauli estão relacionadas ao gerador de rotações, esses operadores de rotação podem ser escritos como exponenciais de matriz com matrizes de Pauli no argumento. Qualquer matriz unitária em SU (2) pode ser escrita como um produto (isto é , circuito em série ) de três portas de rotação ou menos. Observe que, para sistemas de dois níveis, como qubits e spinors , essas rotações têm um período de $4π$ . Uma rotação de $2π$ (360 graus) retorna o mesmo vetor de estado com uma fase diferente. ${\ displaystyle 2 \ vezes 2}$

Nós também temos e para todos ${\ displaystyle R_ {b} (- \ theta) = R_ {b} (\ theta) ^ {\ dagger}}$ ${\ displaystyle R_ {b} (0) = I}$ ${\ displaystyle b \ in \ {x, y, z \}.}$

As matrizes de rotação estão relacionadas às matrizes de Pauli da seguinte maneira: ${\ displaystyle R_ {x} (\ pi) = - iX, R_ {y} (\ pi) = - iY, R_ {z} (\ pi) = - iZ.}$

Portão Hadamard

O portão Hadamard ( francês: [adamaʁ] ) atua em um único qubit. Ele mapeia os estados básicos e (isto é, cria uma superposição se for dado um estado básico). Ele representa uma rotação em torno do eixo na esfera de Bloch . É representado pela matriz Hadamard : ${\ textstyle | 0 \ rangle \ mapsto {\ frac {| 0 \ rangle + | 1 \ rangle} {\ sqrt {2}}}}$ ${\ textstyle | 1 \ rangle \ mapsto {\ frac {| 0 \ rangle - | 1 \ rangle} {\ sqrt {2}}}}$ ${\ displaystyle \ pi}$ ${\ displaystyle ({\ hat {x}} + {\ hat {z}}) / {\ sqrt {2}}}$

Representação do circuito do portão Hadamard

{\ displaystyle H = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 e 1 \\ 1 & -1 \ end {bmatrix}}.}

H é uma matriz involutória . Usando operadores de rotação , temos as identidades: e a porta H controlada também pode ser definida conforme explicado na seção de portas controladas . ${\ displaystyle R_ {y} (\ pi / 2) Z = H}$ ${\ displaystyle XR_ {y} (\ pi / 2) = H.}$

O portão Hadamard pode ser pensado como uma transformação unitária que mapeia operações qubit no eixo z para o eixo x e vice-versa. Por exemplo, , , e . ${\ displaystyle HZH = X}$ ${\ displaystyle H {\ sqrt {X}} \; H = {\ sqrt {Z}} = S}$ ${\ displaystyle HR_ {z} (\ theta) H = R_ {x} (\ theta)}$

Troca de portão

Representação do circuito da porta SWAP

A porta de troca troca dois qubits. Com relação à base , , , , ela é representada pela matriz: ${\ displaystyle | 00 \ rangle}$ ${\ displaystyle | 01 \ rangle}$ ${\ displaystyle | 10 \ rangle}$ ${\ displaystyle | 11 \ rangle}$

{\ displaystyle {\ mbox {SWAP}} = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \ end {bmatrix}}.}

Raiz quadrada da porta de troca

Representação do circuito de √ porta SWAP

A porta √ SWAP executa a meio caminho de uma troca de dois qubit. É universal que qualquer porta de muitos qubit pode ser construída a partir de apenas √ SWAP e portas de qubit simples. A porta √ SWAP não é, entretanto, maximamente emaranhada; mais de uma aplicação dele é necessária para produzir um estado Bell a partir dos estados do produto. Com relação à base , , , , ela é representada pela matriz: ${\ displaystyle | 00 \ rangle}$ ${\ displaystyle | 01 \ rangle}$ ${\ displaystyle | 10 \ rangle}$ ${\ displaystyle | 11 \ rangle}$

{\ displaystyle {\ sqrt {\ text {SWAP}}} = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & {\ frac {1} {2}} (1 + i) & {\ frac {1} {2} } (1-i) & 0 \\ 0 & {\ frac {1} {2}} (1-i) & {\ frac {1} {2}} (1 + i) & 0 \\ 0 & 0 & 0 & 1 \\\ end { bmatrix}}.}

Esta porta surge naturalmente em sistemas que exploram a interação de troca .

Portão Toffoli (CCNOT)

Representação do circuito do portão Toffoli

O portão Toffoli, em homenagem a Tommaso Toffoli ; também chamado de CCNOT gate ou Deutsch gate ; é uma porta de 3 bits, que é universal para computação clássica, mas não para computação quântica. A porta quântica de Toffoli é a mesma porta, definida para 3 qubits. Se nos limitarmos a aceitar apenas os qubits de entrada que são e , então , se os primeiros dois bits estiverem no estado, ele aplicará um Pauli- X (ou NÃO) no terceiro bit, caso contrário, não fará nada. É um exemplo de portão controlado. Uma vez que é o análogo quântico de uma porta clássica, é completamente especificado por sua tabela verdade. A porta Toffoli é universal quando combinada com a porta Hadamard de qubit único. ${\ displaystyle D (\ pi / 2)}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 1 \ rangle}$

Mesa da verdade

Forma de matriz

ENTRADA			SAÍDA
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	0	1
1	1	0	1	1	1
1	1	1	1	1	0

${\ Displaystyle {\ begin {bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\\ end {bmatrix}}}$

A porta de Toffoli está relacionada às operações clássicas AND ( ) e XOR ( ), pois realiza o mapeamento de estados na base computacional. ${\ displaystyle \ land}$ ${\ displaystyle \ oplus}$ ${\ displaystyle | a, b, c \ rangle \ mapsto | a, b, c \ oplus (a \ land b) \ rangle}$

Portão Fredkin (CSWAP)

Representação do circuito do portão Fredkin

A porta Fredkin (também CSWAP ou CS), em homenagem a Edward Fredkin , é uma porta de 3 bits que realiza uma troca controlada . É universal para computação clássica. Ele tem a propriedade útil de que os números de 0s e 1s são conservados ao longo do tempo, o que no modelo de bola de bilhar significa que o mesmo número de bolas é produzido como entrada.

Mesa da verdade

Forma de matriz

ENTRADA			SAÍDA
C	Eu ₁	I ₂	C	O ₁	O ₂
0	0	0	0	0	0
0	0	1	0	0	1
0	1	0	0	1	0
0	1	1	0	1	1
1	0	0	1	0	0
1	0	1	1	1	0
1	1	0	1	0	1
1	1	1	1	1	1

${\ Displaystyle {\ begin {bmatrix} 1 & 0 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 0 & 1 \\\ end {bmatrix}}}$

Portões de acoplamento Ising

As portas de acoplamento Ising R _xx , R _yy e R _zz são portas de 2 qubit que são implementadas nativamente em alguns computadores quânticos de íons presos . Essas portas são definidas como

{\ displaystyle R_ {xx} (\ phi) = \ exp \ left (-i {\ frac {\ phi} {2}} X \ otimes X \ right) = \ cos \ left ({\ frac {\ phi} {2}} \ right) I \ otimes Ii \ sin \ left ({\ frac {\ phi} {2}} \ right) X \ otimes X = {\ begin {bmatrix} \ cos \ left ({\ frac { \ phi} {2}} \ right) & 0 & 0 & -i \ sin \ left ({\ frac {\ phi} {2}} \ right) \\ 0 & \ cos \ left ({\ frac {\ phi} {2} } \ right) & - i \ sin \ left ({\ frac {\ phi} {2}} \ right) & 0 \\ 0 & -i \ sin \ left ({\ frac {\ phi} {2}} \ right ) & \ cos \ left ({\ frac {\ phi} {2}} \ right) & 0 \\ - i \ sin \ left ({\ frac {\ phi} {2}} \ right) & 0 & 0 & \ cos \ left ({\ frac {\ phi} {2}} \ right) \\\ end {bmatrix}},}

{\ displaystyle R_ {yy} (\ phi) = \ exp \ left (-i {\ frac {\ phi} {2}} Y \ otimes Y \ right) = {\ begin {bmatrix} \ cos \ left ({ \ frac {\ phi} {2}} \ right) & 0 & 0 & i \ sin \ left ({\ frac {\ phi} {2}} \ right) \\ 0 & \ cos \ left ({\ frac {\ phi} {2 }} \ right) & - i \ sin \ left ({\ frac {\ phi} {2}} \ right) & 0 \\ 0 & -i \ sin \ left ({\ frac {\ phi} {2}} \ direita) & \ cos \ left ({\ frac {\ phi} {2}} \ right) & 0 \\ i \ sin \ left ({\ frac {\ phi} {2}} \ right) & 0 & 0 & \ cos \ left ({\ frac {\ phi} {2}} \ right) \\\ end {bmatrix}},}

{\ displaystyle R_ {zz} (\ phi) = \ exp \ left (-i {\ frac {\ phi} {2}} Z \ otimes Z \ right) = {\ begin {bmatrix} e ^ {- i \ phi / 2} & 0 & 0 & 0 \\ 0 & e ^ {i \ phi / 2} & 0 & 0 \\ 0 & 0 & e ^ {i \ phi / 2} & 0 \\ 0 & 0 & 0 & e ^ {- i \ phi / 2} \\\ end {bmatrix}}. }

Troca imaginária (iSWAP)

Para sistemas com interações do tipo Ising, às vezes é mais natural introduzir a troca imaginária ou porta iSWAP definida como

{\ displaystyle i {\ mbox {SWAP}} = \ exp \ left [i {\ frac {\ pi} {4}} (X \ otimes X + Y \ otimes Y) \ right] = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 0 & i & 0 \\ 0 & i & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 \ end {bmatrix}},}

onde sua versão raiz quadrada é dada por

{\ displaystyle {\ sqrt {i {\ mbox {SWAP}}}} = \ exp \ left [i {\ frac {\ pi} {8}} (X \ otimes X + Y \ otimes Y) \ right] = {\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & {\ frac {1} {\ sqrt {2}}} & {\ frac {i} {\ sqrt {2}}} & 0 \\ 0 & {\ frac {i} { \ sqrt {2}}} & {\ frac {1} {\ sqrt {2}}} & 0 \\ 0 & 0 & 0 & 0 & 1 \ end {bmatrix}}.}

Observe isso e comute, então e . ${\ displaystyle X \ otimes X}$ ${\ displaystyle Y \ otimes Y}$ ${\ displaystyle i {\ mbox {SWAP}} = R_ {xx} (- \ pi / 2) R_ {yy} (- \ pi / 2)}$ ${\ displaystyle {\ sqrt {i {\ mbox {SWAP}}}} = R_ {xx} (- \ pi / 4) R_ {yy} (- \ pi / 4)}$

Portão alemão

O portão Deutsch (ou ), em homenagem ao físico David Deutsch é um portão de três qubit. É definido como ${\ displaystyle D _ {\ theta}}$

{\ displaystyle | a, b, c \ rangle \ mapsto {\ begin {cases} i \ cos (\ theta) | a, b, c \ rangle + \ sin (\ theta) | a, b, 1-c \ rangle & {\ mbox {for}} a = b = 1 \\ | a, b, c \ rangle & {\ mbox {caso contrário.}} \ end {cases}}}

Infelizmente, um Deutsch gate em funcionamento permaneceu fora de alcance, devido à falta de um protocolo. Existem algumas propostas para realizar uma porta Deutsch com interação dipolo-dipolo em átomos neutros.

Portas quânticas universais

Ambos CNOT e são portas universais de dois qubit e podem ser transformados um no outro.

{\ displaystyle {\ sqrt {\ mbox {SWAP}}}}

Um conjunto de portas quânticas universais é qualquer conjunto de portas para as quais qualquer operação possível em um computador quântico pode ser reduzida, ou seja, qualquer outra operação unitária pode ser expressa como uma sequência finita de portas do conjunto. Tecnicamente, isso é impossível com qualquer coisa menos do que um conjunto incontável de portas, uma vez que o número de portas quânticas possíveis é incontável, enquanto o número de sequências finitas de um conjunto finito é contável . Para resolver esse problema, exigimos apenas que qualquer operação quântica possa ser aproximada por uma sequência de portas desse conjunto finito. Além disso, para unidades em um número constante de qubits, o teorema de Solovay-Kitaev garante que isso pode ser feito de forma eficiente.

Os operadores de rotação $R x (θ)$ , $R y (θ)$ , $R z (θ)$ , a porta de deslocamento de fase $P (φ)$ e CNOT formam um conjunto universal amplamente utilizado de portas quânticas.

Um conjunto de porta universal comum é a Clifford + T conjunto porta, que é composto das cnot, H , S e T portões. O conjunto de Clifford sozinho não é universal e pode ser simulado com eficiência classicamente pelo teorema de Gottesman-Knill .

A porta Toffoli forma um conjunto de portas universais para circuitos lógicos reversíveis. Um conjunto de portas quânticas universais de duas portas contendo uma porta de Toffoli pode ser construído adicionando-se a porta Hadamard ao conjunto.

Um conjunto de portas quânticas universais de porta única também pode ser formulado usando a porta Deutsch de três qubit . ${\ displaystyle D (\ theta)}$

Uma porta lógica universal para computação clássica reversível, a porta Toffoli, é redutível à porta Deutsch , mostrando assim que todas as operações lógicas clássicas reversíveis podem ser realizadas em um computador quântico universal. ${\ displaystyle D ({\ begin {matrix} {\ frac {\ pi} {2}} \ end {matrix}})}$

Também existe uma única porta de dois qubits suficiente para universalidade, visto que pode ser aplicada a quaisquer pares de qubits em um circuito de largura . ${\ displaystyle (k, k + 1) \ mod n}$ ${\ displaystyle n}$

Composição do circuito

Portões com fiação serial

Duas portas Y e X em série. A ordem em que aparecem no fio é invertida ao multiplicá-los.

Suponha que temos duas portas A e B , que ambas atuam nos qubits. Quando B é colocado depois de um em um circuito em série, então o efeito das duas portas podem ser descrita como uma única porta C . ${\ displaystyle n}$

{\ displaystyle C = B \ cdot A}

Onde está a multiplicação da matriz . O portão resultando C terão as mesmas dimensões que A e B . A ordem em que as portas apareceriam em um diagrama de circuito é invertida ao multiplicá-las. ${\ displaystyle \ cdot}$

Por exemplo, colocar a porta Pauli X após a porta Pauli Y , ambas atuando em um único qubit, pode ser descrito como uma única porta C combinada :

{\ displaystyle C = X \ cdot Y = {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix}} \ cdot {\ begin {bmatrix} 0 & -i \\ i & 0 \ end {bmatrix}} = {\ begin {bmatriz} i & 0 \\ 0 & -i \ end {bmatriz}}}

O símbolo do produto ( ) é freqüentemente omitido. ${\ displaystyle \ cdot}$

Expoentes de portas quânticas

Todos os expoentes reais de matrizes unitárias também são matrizes unitárias e todas as portas quânticas são matrizes unitárias.

Os expoentes inteiros positivos são equivalentes a sequências de portas conectadas em série (por exemplo ), e os expoentes reais são uma generalização do circuito em série. Por exemplo, e são portas quânticas válidas. ${\ displaystyle X ^ {3} = X \ cdot X \ cdot X}$ ${\ displaystyle X ^ {\ pi}}$ ${\ displaystyle {\ sqrt {X}} = X ^ {1/2}}$

${\ displaystyle U ^ {0} = I}$ para qualquer matriz unitária . A matriz de identidade ( ) se comporta como um NOP e pode ser representada como fio desencapado em circuitos quânticos ou nem mesmo ser mostrada. ${\ displaystyle U}$ ${\ displaystyle I}$

Todas as portas são matrizes unitárias, de modo que e , onde está o conjugado transposto . Isto significa que expoente negativo de portões são inversos unitárias dos seus homólogos exponenciadas positivamente: . Por exemplo, alguns expoentes negativos das portas de deslocamento de fase são e . ${\ displaystyle U ^ {\ dagger} U = UU ^ {\ dagger} = I}$ ${\ displaystyle U ^ {\ dagger} = U ^ {- 1}}$ ${\ displaystyle \ dagger}$ ${\ displaystyle U ^ {- n} = (U ^ {n}) ^ {\ dagger}}$ ${\ displaystyle T ^ {- 1} = T ^ {\ dagger}}$ ${\ displaystyle T ^ {- 2} = (T ^ {2}) ^ {\ dagger} = S ^ {\ dagger}}$

Portões paralelos

Duas portas e em paralelo equivale à porta

{\ displaystyle Y}

{\ displaystyle X}

{\ displaystyle Y \ otimes X}

O produto tensorial (ou produto de Kronecker ) de duas portas quânticas é a porta que é igual às duas portas em paralelo.

Se nós, como na imagem, combinarmos a porta Pauli- Y com a porta Pauli- X em paralelo, isso pode ser escrito como:

{\ displaystyle C = Y \ otimes X = {\ begin {bmatrix} 0 & -i \\ i & 0 \ end {bmatrix}} \ otimes {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix}} = {\ begin {bmatrix} 0 {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix}} & - i {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix}} \\ i {\ begin {bmatrix} 0 & 1 \ \ 1 & 0 \ end {bmatrix}} & 0 {\ begin {bmatrix} 0 & 1 \\ 1 & 0 \ end {bmatrix}} \ end {bmatrix}} = {\ begin {bmatrix} 0 & 0 & 0 & -i \\ 0 & 0 & -i & 0 \\ 0 & i & 0 & 0 \ \ i & 0 & 0 & 0 \ end {bmatrix}}}

Tanto a porta Pauli- X quanto a porta Pauli- Y agem em um único qubit. A porta resultante atua em dois qubits. ${\ displaystyle C}$

Transformada de Hadamard

A porta é a porta Hadamard ( ) aplicada em paralelo em 2 qubits. Pode ser escrito como: ${\ displaystyle H_ {2} = H \ otimes H}$ ${\ displaystyle H}$

{\ displaystyle H_ {2} = H \ otimes H = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 & 1 \\ 1 & -1 \ end {bmatrix}} \ otimes {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 & 1 \\ 1 & -1 \ end {bmatrix}} = {\ frac {1} {2}} {\ begin {bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \ end {bmatrix}}}

Esta "porta de Hadamard paralela de dois qubit" irá, quando aplicada, por exemplo, ao vetor zero de dois qubit ( ), ${\ displaystyle | 00 \ rangle}$ criar um estado quântico que tem igual probabilidade de ser observado em qualquer um de seus quatro resultados possíveis; , , , E . Podemos escrever esta operação como: ${\ displaystyle | 00 \ rangle}$ ${\ displaystyle | 01 \ rangle}$ ${\ displaystyle | 10 \ rangle}$ ${\ displaystyle | 11 \ rangle}$

{\ displaystyle H_ {2} | 00 \ rangle = {\ frac {1} {2}} {\ begin {bmatrix} 1 & 1 & 1 & 1 \\ 1 & -1 & 1 & -1 \\ 1 & 1 & -1 & -1 \\ 1 & -1 & -1 & 1 \ end {bmatrix}} {\ begin {bmatrix} 1 \\ 0 \\ 0 \\ 0 \ end {bmatrix}} = {\ frac {1} {2}} {\ begin {bmatrix} 1 \\ 1 \ \ 1 \\ 1 \ end {bmatrix}} = {\ frac {1} {2}} | 00 \ rangle + {\ frac {1} {2}} | 01 \ rangle + {\ frac {1} {2 }} | 10 \ rangle + {\ frac {1} {2}} | 11 \ rangle = {\ frac {| 00 \ rangle + | 01 \ rangle + | 10 \ rangle + | 11 \ rangle} {2}} }

Exemplo: A transformação de Hadamard em um registrador de 3 qubit .

{\ displaystyle | \ psi \ rangle}

Aqui, a amplitude de cada estado mensurável é 1 ⁄ 2 . A probabilidade de observar qualquer estado é o quadrado do valor absoluto da amplitude dos estados mensuráveis, o que no exemplo acima significa que há um em cada quatro que observamos qualquer um dos quatro casos individuais. Veja medição para detalhes.

${\ displaystyle H_ {2}}$ executa a transformação de Hadamard em dois qubits. Da mesma forma, a porta realiza uma transformação Hadamard em um registrador de qubits. ${\ displaystyle \ underbrace {H \ otimes H \ otimes \ dots \ otimes H} _ {n {\ text {times}}} = \ bigotimes _ {1} ^ {n} H = H ^ {\ otimes n} = H_ {n}}$ ${\ displaystyle n}$

Quando aplicada a um registro de qubits todos inicializados , a transformada de Hadamard coloca o registro quântico em uma superposição com igual probabilidade de ser medido em qualquer um de seus possíveis estados: ${\ displaystyle n}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle 2 ^ {n}}$

{\ displaystyle \ bigotimes _ {0} ^ {n-1} H | 0 \ rangle = {\ Big (} \ bigotimes _ {0} ^ {n-1} H {\ Big)} {\ Big (} \ intolerância _ {0} ^ {n-1} | 0 \ rangle {\ Big)} = {\ frac {1} {\ sqrt {2 ^ {n}}}} {\ begin {bmatrix} 1 \\ 1 \ \\ vdots \\ 1 \ end {bmatrix}} = {\ frac {1} {\ sqrt {2 ^ {n}}}} {\ Big (} | 0 \ rangle + | 1 \ rangle + \ dots + | 2 ^ {n} -1 \ rangle {\ Big)} = {\ frac {1} {\ sqrt {2 ^ {n}}}} \ sum _ {i = 0} ^ {2 ^ {n} -1 } | i \ rangle}

Este estado é uma superposição uniforme e é gerado como a primeira etapa em alguns algoritmos de pesquisa, por exemplo, na amplificação de amplitude e estimativa de fase .

Medir esse estado resulta em um número aleatório entre e . O quão aleatório o número é depende da fidelidade das portas lógicas. Se não for medido, é um estado quântico com amplitude de probabilidade igual para cada um de seus estados possíveis. ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 2 ^ {n} -1 \ rangle}$ ${\ displaystyle {\ frac {1} {\ sqrt {2 ^ {n}}}}}$

A transformação de Hadamard atua em um registro com qubits da seguinte maneira: ${\ displaystyle | \ psi \ rangle}$ ${\ displaystyle n}$ ${\ textstyle | \ psi \ rangle = \ bigotimes _ {i = 0} ^ {n-1} | \ psi _ {i} \ rangle}$

{\ displaystyle \ bigotimes _ {0} ^ {n-1} H | \ psi \ rangle = \ bigotimes _ {i = 0} ^ {n-1} {\ frac {| 0 \ rangle + (- 1) ^ {\ psi _ {i}} | 1 \ rangle} {\ sqrt {2}}} = {\ frac {1} {\ sqrt {2 ^ {n}}}} \ bigotimes _ {i = 0} ^ { n-1} {\ Big (} | 0 \ rangle + (- 1) ^ {\ psi _ {i}} | 1 \ rangle {\ Big)} = H | \ psi _ {0} \ rangle \ otimes H | \ psi _ {1} \ rangle \ otimes \ cdots \ otimes H | \ psi _ {n-1} \ rangle}

Aplicação em estados emaranhados

Se dois ou mais qubits são vistos como um único estado quântico, este estado combinado é igual ao produto tensorial dos qubits constituintes. Qualquer estado que pode ser escrito como um produto tensorial dos subsistemas constituintes é chamado de estados separáveis . Por outro lado, um estado emaranhado é qualquer estado que não pode ser fatorado por tensor, ou em outras palavras: Um estado emaranhado não pode ser escrito como um produto tensorial de seus estados qubits constituintes. Cuidado especial deve ser tomado ao aplicar portas a qubits constituintes que formam estados emaranhados.

Se tivermos um conjunto de N qubits que estão emaranhados e desejarmos aplicar uma porta quântica em M < N qubits no conjunto, teremos que estender a porta para receber N qubits. Esta aplicação pode ser feita combinando a porta com uma matriz de identidade de modo que seu produto tensorial se torne uma porta que atua sobre N qubits. A matriz de identidade ( ) ${\ displaystyle I}$ é uma representação da porta que mapeia cada estado para si mesma (ou seja, não faz nada). Em um diagrama de circuito, a porta de identidade ou matriz frequentemente aparecerá como apenas um fio desencapado.

O exemplo dado no texto. A porta Hadamard age apenas em 1 qubit, mas é um estado quântico emaranhado que se estende por 2 qubits. Em nosso exemplo,

{\ displaystyle H}

{\ displaystyle | \ psi \ rangle}

{\ displaystyle | \ psi \ rangle = {\ frac {| 00 \ rangle + | 11 \ rangle} {\ sqrt {2}}}}

Por exemplo, a porta Hadamard ( ) ${\ displaystyle H}$ atua em um único qubit, mas se, por exemplo, alimentá-lo com o primeiro dos dois qubits que constituem o estado de Bell emaranhado , não podemos escrever essa operação facilmente. Precisamos estender a porta Hadamard com a porta de identidade para que possamos agir em estados quânticos que abrangem dois qubits: ${\ displaystyle {\ frac {| 00 \ rangle + | 11 \ rangle} {\ sqrt {2}}}}$ ${\ displaystyle H}$ ${\ displaystyle I}$

{\ displaystyle K = H \ otimes I = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 & 1 \\ 1 & -1 \ end {bmatrix}} \ otimes {\ begin {bmatrix} 1 & 0 \\ 0 & 1 \ end {bmatrix}} = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \ end {bmatrix} }}

A porta agora pode ser aplicada a qualquer estado de dois qubit, entrelaçado ou não. O portão deixará o segundo qubit intocado e aplicará a transformação de Hadamard ao primeiro qubit. Se aplicado ao estado Bell em nosso exemplo, podemos escrever como: ${\ displaystyle K}$ ${\ displaystyle K}$

{\ displaystyle K {\ frac {| 00 \ rangle + | 11 \ rangle} {\ sqrt {2}}} = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 & 0 & 1 & 0 \\ 0 & 1 & 0 & 1 \\ 1 & 0 & -1 & 0 \\ 0 & 1 & 0 & -1 \ end {bmatrix}} {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 \\ 0 \\ 0 \\ 1 \ end { bmatrix}} = {\ frac {1} {2}} {\ begin {bmatrix} 1 \\ 1 \\ 1 \\ - 1 \ end {bmatrix}} = {\ frac {| 00 \ rangle + | 01 \ rangle + | 10 \ rangle - | 11 \ rangle} {2}}}

Complexidade computacional e o produto tensorial

A complexidade de tempo para multiplicar duas matrizes é de pelo menos , se estiver usando uma máquina clássica. Como o tamanho de uma porta que opera em qubits é , significa que o tempo para simular uma etapa em um circuito quântico (por meio da multiplicação das portas) que opera em estados emaranhados genéricos é . Por esta razão, acredita-se que é intratável simular grandes sistemas quânticos emaranhados usando computadores clássicos. Subconjuntos de portas, como as portas de Clifford , ou o caso trivial de circuitos que implementam apenas funções booleanas clássicas (por exemplo, combinações de X , CNOT , Toffoli ), podem, entretanto, ser simulados com eficiência em computadores clássicos. ${\ displaystyle n \ times n}$ ${\ displaystyle \ Omega (n ^ {2} \ log n)}$ ${\ displaystyle q}$ ${\ displaystyle 2 ^ {q} \ times 2 ^ {q}}$ ${\ displaystyle \ Omega ({2 ^ {q}} ^ {2} \ log ({2 ^ {q}}))}$

O vetor de estado de um registrador quântico com qubits são entradas complexas. Armazenar as amplitudes de probabilidade como uma lista de valores de ponto flutuante não é tratável para grandes . ${\ displaystyle n}$ ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle n}$

Inversão unitária de portões

Exemplo: O inverso unitário do produto Hadamard-CNOT. As três portas , e são seus próprios inversos unitários.

{\ displaystyle H}

{\ displaystyle I}

{\ displaystyle \ mathrm {CNOT}}

Como todas as portas lógicas quânticas são reversíveis , qualquer composição de portas múltiplas também é reversível. Todos os produtos e produtos tensores (ou seja, séries e combinações paralelas ) de matrizes unitárias também são matrizes unitárias. Isso significa que é possível construir um inverso de todos os algoritmos e funções, desde que contenham apenas portas.

Inicialização, medição, E / S e decoerência espontânea são efeitos colaterais em computadores quânticos. Os portões, entretanto, são puramente funcionais e bijetivos .

Se for uma matriz unitária , então e . O punhal ( ) denota o conjugado complexo da transposta . É também chamado de adjunto de Hermit . ${\ displaystyle U}$ ${\ displaystyle U ^ {\ dagger} U = UU ^ {\ dagger} = I}$ ${\ displaystyle U ^ {\ dagger} = U ^ {- 1}}$ ${\ displaystyle \ dagger}$

Se uma função é um produto de portas , o inverso unitário da função pode ser construído: ${\ displaystyle F}$ ${\ displaystyle m}$ ${\ displaystyle F = A_ {1} \ cdot A_ {2} \ cdot \ dots \ cdot A_ {m}}$ ${\ displaystyle F ^ {\ dagger}}$

Porque temos, após aplicação repetida em si mesmo ${\ displaystyle (UV) ^ {\ dagger} = V ^ {\ dagger} U ^ {\ dagger}}$

{\ displaystyle F ^ {\ dagger} = \ left (\ prod _ {0 <i \ leq m} A_ {i} \ right) ^ {\ dagger} = \ prod _ {0 \ leq i <m} A_ { mi} ^ {\ dagger} = A_ {m} ^ {\ dagger} \ cdot \ dots \ cdot A_ {2} ^ {\ dagger} \ cdot A_ {1} ^ {\ dagger}}

Da mesma forma, se a função consiste em duas portas e em paralelo, então e . ${\ displaystyle G}$ ${\ displaystyle A}$ ${\ displaystyle B}$ ${\ displaystyle G = A \ otimes B}$ ${\ displaystyle G ^ {\ dagger} = (A \ otimes B) ^ {\ dagger} = A ^ {\ dagger} \ otimes B ^ {\ dagger}}$

Portões que são seus próprios inversos unitários são chamados de operadores hermitianos ou auto-adjuntos . Algumas portas elementares, como as portas Hadamard ( H ) e Pauli ( I , X , Y , Z ) são operadores Hermitianos, enquanto outras como as portas de mudança de fase ( S , T , P , CPHASE) geralmente não são. Portões que não são hermitianos são chamados de skew-hermitian ou operadores adjuntos .

Por exemplo, um algoritmo de adição pode ser usado para subtração, se estiver sendo "executado ao contrário", como seu inverso unitário. A transformada quântica inversa de Fourier é a inversa unitária. Inversos unitários também podem ser usados para descomputação . Linguagens de programação para computadores quânticos, tais como Microsoft 's Q # e de Bernhard Ömer QCL , contêm função de inversão como conceitos de programação.

Medição

Representação do circuito de medição. As duas linhas do lado direito representam um bit clássico e a única linha do lado esquerdo representa um qubit.

A medição (às vezes chamada de observação ) é irreversível e, portanto, não é uma porta quântica, porque atribui o estado quântico observado a um único valor. A medição toma um estado quântico e o projeta para um dos vetores de base , com uma probabilidade igual ao quadrado da profundidade do vetor (a norma é o módulo ao quadrado) ao longo desse vetor de base. Isso é conhecido como regra de Born e aparece como uma operação estocástica irreversível, uma vez que define probabilisticamente o estado quântico igual ao vetor de base que representa o estado medido (o estado " colapsa " para um valor único definido). Por que e como, ou mesmo se o estado quântico entra em colapso na medição, é chamado de problema de medição .

A probabilidade de medir um valor com amplitude de probabilidade é , onde está o módulo . ${\ displaystyle \ phi}$ ${\ displaystyle 1 \ geq | \ phi | ^ {2} \ geq 0}$ ${\ displaystyle | \ cdot |}$

Medindo um único qubit, cujo estado quântico é representado pelo vetor , irá resultar em com probabilidade , e com probabilidade . ${\ displaystyle a | 0 \ rangle + b | 1 \ rangle = {\ begin {bmatrix} a \\ b \ end {bmatrix}}}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | a | ^ {2}}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | b | ^ {2}}$

Por exemplo, medir um qubit com o estado quântico renderá com igual probabilidade ou . ${\ displaystyle {\ frac {| 0 \ rangle -i | 1 \ rangle} {\ sqrt {2}}} = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 \\ -i \ end {bmatrix}}}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 1 \ rangle}$

Para um único qubit, temos uma esfera unitária com o estado quântico tal que . O estado pode ser reescrito como , ou e . Nota: é a probabilidade de medir e é a probabilidade de medir .

{\ displaystyle \ mathbb {C} ^ {2}}

{\ displaystyle a | 0 \ rangle + b | 1 \ rangle}

{\ displaystyle | a | ^ {2} + | b | ^ {2} = 1}

{\ displaystyle | \ cos \ theta | ^ {2} + | \ sin \ theta | ^ {2} = 1}

{\ displaystyle | a | ^ {2} = \ cos ^ {2} \ theta}

{\ displaystyle | b | ^ {2} = \ sin ^ {2} \ theta}

{\ displaystyle | a | ^ {2}}

{\ displaystyle | 0 \ rangle}

{\ displaystyle | b | ^ {2}}

{\ displaystyle | 1 \ rangle}

Um estado quântico que vãos $n$ qubits pode ser escrito como um vector em complexos dimensões: . Isso ocorre porque o produto tensorial de $n$ qubits é um vetor em dimensões. Dessa forma, um registro de $n$ qubits pode ser medido em estados distintos, semelhante a como um registro de $n$ bits clássicos pode conter estados distintos. Ao contrário dos bits dos computadores clássicos, os estados quânticos podem ter amplitudes de probabilidade diferentes de zero em vários valores mensuráveis simultaneamente. Isso é chamado de superposição . ${\ displaystyle | \ Psi \ rangle}$ ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle | \ Psi \ rangle \ in \ mathbb {C} ^ {2 ^ {n}}}$ ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle 2 ^ {n}}$

A soma de todas as probabilidades para todos os resultados deve ser sempre igual a 1 . Outra maneira de dizer isso é que o teorema de Pitágoras generalizado para tem que todos os estados quânticos com $n$ qubits devem satisfazer , onde é a amplitude de probabilidade para o estado mensurável . Uma interpretação geométrica deste é que o possível valor-espaço de um estado quântico com $n$ qubits é a superfície de uma esfera unitária em e que as transformações unitárias (por exemplo, rede de portas lógicas quântica) aplicada a ele são rotações sobre a esfera. As rotações que as portas executam estão no grupo de simetria U (2 ⁿ ) . A medição é, então, uma projeção probabilística dos pontos na superfície dessa esfera complexa sobre os vetores básicos que abrangem o espaço (e rotulam os resultados). ${\ displaystyle \ mathbb {C} ^ {2 ^ {n}}}$ ${\ displaystyle | \ Psi \ rangle}$ ${\ textstyle 1 = \ sum _ {x = 0} ^ {2 ^ {n} -1} | a_ {x} | ^ {2}}$ ${\ displaystyle a_ {x}}$ ${\ displaystyle | x \ rangle}$ ${\ displaystyle | \ Psi \ rangle}$ ${\ displaystyle \ mathbb {C} ^ {2 ^ {n}}}$

Em muitos casos, o espaço é representado como um espaço de Hilbert em vez de algum espaço complexo dimensional específico . O número de dimensões (definido pelos vetores de base e, portanto, também os resultados possíveis da medição) é então frequentemente implícito pelos operandos, por exemplo, como o espaço de estado necessário para resolver um problema . No algoritmo de Grover , Lov chamou esse conjunto de vetores de base genérico de "banco de dados" . ${\ displaystyle {\ mathcal {H}}}$ ${\ displaystyle 2 ^ {n}}$

A seleção de vetores de base para medir um estado quântico influenciará o resultado da medição. Consulte a mudança de base e a entropia de Von Neumann para obter detalhes. Neste artigo, sempre usamos a base computacional , o que significa que rotulamos os vetores de base de um registrador $n-$ qubit , ou usamos a representação binária . ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle | 0 \ rangle, | 1 \ rangle, | 2 \ rangle, \ cdots, | 2 ^ {n} -1 \ rangle}$ ${\ displaystyle | 0_ {10} \ rangle = | 0 \ dots 00_ {2} \ rangle, | 1_ {10} \ rangle = | 0 \ dots 01_ {2} \ rangle, | 2_ {10} \ rangle = | 0 \ dots 10_ {2} \ rangle, \ cdots, | 2 ^ {n} -1 \ rangle = | 111 \ dots 1_ {2} \ rangle}$

No domínio da computação quântica, geralmente é assumido que os vetores de base constituem uma base ortonormal .

Um exemplo de uso de uma base de medição alternativa está na cifra BB84 .

O efeito da medição em estados emaranhados

A porta Hadamard - CNOT , que quando dada a entrada produz um estado Bell .

{\ displaystyle | 00 \ rangle}

Se dois estados quânticos (ou seja , qubits ou registradores ) estão emaranhados (o que significa que seu estado combinado não pode ser expresso como um produto tensorial ), a medição de um registro afeta ou revela o estado do outro registro, colapsando parcial ou totalmente seu estado também. Este efeito pode ser usado para computação e em muitos algoritmos.

A combinação Hadamard-CNOT atua no estado zero da seguinte forma:

{\ displaystyle \ operatorname {CNOT} (H \ otimes I) | 00 \ rangle = \ left ({\ begin {bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \ end {bmatrix}} \ left ({\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 & 1 \\ 1 & -1 \ end {bmatrix}} \ otimes {\ begin {bmatrix} 1 e 0 \\ 0 & 1 \ end {bmatrix}} \ right) \ right) {\ begin {bmatrix} 1 \\ 0 \\ 0 \\ 0 \ end {bmatrix}} = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 \\ 0 \\ 0 \\ 1 \ end {bmatrix}} = {\ frac {| 00 \ rangle + | 11 \ rangle} {\ sqrt {2}}}}

O estado de Bell no texto é onde e . Portanto, pode ser descrito pelo plano complexo medido pelos vetores de base e , como na imagem. A esfera unitária (in ) que representa o espaço de valor possível do sistema de 2 qubit cruza o plano e fica na superfície das esferas unitárias. Porque , há probabilidade igual de medir este estado para ou , e probabilidade zero de medi-lo para ou .

{\ displaystyle | \ Psi \ rangle = a | 00 \ rangle + b | 01 \ rangle + c | 10 \ rangle + d | 11 \ rangle}

{\ displaystyle a = d = {\ frac {1} {\ sqrt {2}}}}

{\ displaystyle b = c = 0}

{\ displaystyle | 00 \ rangle}

{\ displaystyle | 11 \ rangle}

{\ displaystyle \ mathbb {C} ^ {4}}

{\ displaystyle | \ Psi \ rangle}

{\ displaystyle | a | ^ {2} = | d | ^ {2} = 1/2}

{\ displaystyle | 00 \ rangle}

{\ displaystyle | 11 \ rangle}

{\ displaystyle | 01 \ rangle}

{\ displaystyle | 10 \ rangle}

Este estado resultante é o estado Bell . Não pode ser descrito como um produto tensorial de dois qubits. Não há solução para ${\ displaystyle {\ frac {| 00 \ rangle + | 11 \ rangle} {\ sqrt {2}}} = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 \\ 0 \\ 0 \\ 1 \ end {bmatrix}}}$

{\ displaystyle {\ begin {bmatrix} x \\ y \ end {bmatrix}} \ otimes {\ begin {bmatrix} w \\ z \ end {bmatrix}} = {\ begin {bmatrix} xw \\ xz \\ yw \\ yz \ end {bmatrix}} = {\ frac {1} {\ sqrt {2}}} {\ begin {bmatrix} 1 \\ 0 \\ 0 \\ 1 \ end {bmatrix}}}

porque, por exemplo, $w$ precisa ser diferente de zero e zero no caso de $xw$ e $yw$ .

O estado quântico abrange os dois qubits. Isso é chamado de emaranhamento . Medindo um dos dois qubits que compõem este estado de Bell irá resultar em que o outro qubit logicamente deve ter o mesmo valor, tanto deve ser o mesmo: ou ela será encontrada no estado , ou no estado . Se medirmos um dos qubits como sendo, por exemplo , então o outro qubit também deve ser , porque seu estado combinado se tornou . A medição de um dos qubits causa o colapso de todo o estado quântico, que abrange os dois qubits. ${\ displaystyle | 00 \ rangle}$ ${\ displaystyle | 11 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 1 \ rangle}$ ${\ displaystyle | 11 \ rangle}$

O estado GHZ é um estado quântico emaranhado semelhante que abrange três ou mais qubits.

Este tipo de atribuição de valor ocorre instantaneamente em qualquer distância e isso foi verificado experimentalmente em 2018 pelo QUESS para distâncias de até 1200 quilômetros. O fato de o fenômeno parecer acontecer instantaneamente em oposição ao tempo que levaria para percorrer a distância que separa os qubits na velocidade da luz é chamado de paradoxo EPR , e é uma questão em aberto na física como resolver isso. Originalmente, foi resolvido abandonando o pressuposto do realismo local , mas outras interpretações também surgiram. Para obter mais informações, consulte os experimentos de teste de Bell . O teorema da não comunicação prova que esse fenômeno não pode ser usado para uma comunicação mais rápida que a luz de informações clássicas .

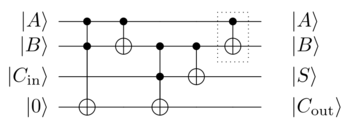
Medição em registros com qubits emaranhados em pares

O efeito de uma transformada unitária F em um registrador A que está em uma superposição de estados e emaranhados em pares com o registrador B. Aqui,

n

é 3 (cada registrador tem 3 qubits).

{\ displaystyle 2 ^ {n}}

Tomar um registo A com $n$ qubits todos inicializado para , e alimentá-lo através de um paralelo Hadamard portão . O registro A entrará então no estado que tem probabilidade igual de quando medido em qualquer um de seus estados possíveis; a . Pegue um segundo registro B, também com $n$ qubits inicializados para e CNOT em pares seus qubits com os qubits no registro A, de modo que para cada $p$ os qubits e formam o estado . ${\ displaystyle | 0 \ rangle}$ ${\ textstyle \ bigotimes _ {1} ^ {n} H}$ ${\ textstyle {\ frac {1} {\ sqrt {2 ^ {n}}}} \ sum _ {k = 0} ^ {2 ^ {n} -1} | k \ rangle}$ ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle | 2 ^ {n} -1 \ rangle}$ ${\ displaystyle | 0 \ rangle}$ ${\ displaystyle A_ {p}}$ ${\ displaystyle B_ {p}}$ ${\ displaystyle | A_ {p} B_ {p} \ rangle = {\ frac {| 00 \ rangle + | 11 \ rangle} {\ sqrt {2}}}}$

Se agora medir os qubits em registo A, então registar-B será encontrada para conter o mesmo valor que A. Se no entanto em vez disso aplicar uma porta lógica quântica $M$ em A e, em seguida, medir, em seguida , em que é o inverso unitária de $F$ . ${\ displaystyle | A \ rangle = F | B \ rangle \ iff F ^ {\ dagger} | A \ rangle = | B \ rangle}$ ${\ displaystyle F ^ {\ dagger}}$

Por causa de como atuam inversos unitários de portas ,. Por exemplo, digamos , então . ${\ displaystyle F ^ {\ dagger} | A \ rangle = F ^ {- 1} (| A \ rangle) = | B \ rangle}$ ${\ displaystyle F (x) = x + 3 {\ pmod {2 ^ {n}}}}$ ${\ displaystyle | B \ rangle = | A-3 {\ pmod {2 ^ {n}}} \ rangle}$

A igualdade manter-se-á independentemente da ordem em que a medição é efectuada (nos registos A ou B), assumindo que $F$ foi executado até ao fim. A medição pode até ser intercalada aleatoriamente e simultaneamente qubit por qubit, uma vez que a atribuição de medições de um qubit limitará o espaço de valor possível dos outros qubits emaranhados.

Mesmo que as igualdades se mantenham, as probabilidades para medir os resultados possíveis podem mudar como resultado da aplicação de $F$ , como pode ser a intenção em um algoritmo de busca quântica.

Este efeito de compartilhamento de valor via emaranhamento é usado no algoritmo de Shor , estimativa de fase e na contagem quântica . Usar a transformada de Fourier para amplificar as amplitudes de probabilidade dos estados de solução para algum problema é um método genérico conhecido como " pesca de Fourier ".

Síntese de função lógica

As funções e rotinas que usam apenas portas podem ser descritas como matrizes, assim como as portas menores. A matriz que representa uma função quântica que atua sobre qubits tem o tamanho . Por exemplo, uma função que atua em um "qubyte" (um registrador de 8 qubits) seria descrita como uma matriz com elementos. ${\ displaystyle q}$ ${\ displaystyle 2 ^ {q} \ times 2 ^ {q}}$ ${\ displaystyle 2 ^ {8} \ times 2 ^ {8} = 256 \ vezes 256}$

As transformações unitárias que não estão no conjunto de portas nativamente disponíveis no computador quântico (as portas primitivas) podem ser sintetizadas, ou aproximadas, combinando as portas primitivas disponíveis em um circuito . Uma maneira de fazer isso é fatorar a matriz que codifica a transformação unitária em um produto de produtos tensores (isto é, circuitos em série e paralelos ) das portas primitivas disponíveis. O grupo U (2 ^q ) é o grupo de simetria para as portas que atuam nos qubits. A fatoração é, então, o problema de encontrar um caminho em U (2 ^q ) a partir do conjunto gerador de portas primitivas. O teorema de Solovay-Kitaev mostra que dado um conjunto suficiente de portas primitivas, existe uma aproximação eficiente para qualquer porta. Para o caso geral com grande número de qubits, essa abordagem direta à síntese de circuitos é intratável . ${\ displaystyle q}$

Como as portas são de natureza unitária , todas as funções devem ser reversíveis e sempre ser mapeamentos bijetivos de entrada para saída. Deve sempre existir uma função como essa . As funções que não são invertíveis podem ser tornadas invertíveis adicionando qubits de ancilla à entrada ou à saída, ou ambos. Depois que a função foi executada até a conclusão, os qubits ancilla podem ser não computados ou deixados intactos. Medir ou colapsar o estado quântico de um qubit ancilla (por exemplo, pela reinicialização do valor dele, ou por sua descoerência espontânea ) que não foi computado pode resultar em erros, pois seu estado pode estar emaranhado com os qubits que ainda estão sendo usado em cálculos. ${\ displaystyle F ^ {- 1}}$ ${\ displaystyle F ^ {- 1} (F (| \ psi \ rangle)) = | \ psi \ rangle}$

Operações logicamente irreversíveis, para o módulo exemplo adição de dois -qubit regista a e b, , pode ser feita logicamente reversível pela adição de informações para a saída, de modo que a entrada pode ser calculado a partir da saída (ou seja, não existe uma função ). No nosso exemplo, isto pode ser feito através da transmissão de um dos registos de entrada para a saída: . A saída pode então ser usada para calcular a entrada (isto é, dada a saída e , podemos facilmente encontrar a entrada; é fornecida e ) e a função torna-se bijetiva. ${\ displaystyle 2 ^ {n}}$ ${\ displaystyle n}$ ${\ displaystyle F (a, b) = a + b {\ pmod {2 ^ {n}}}}$ ${\ displaystyle F ^ {- 1}}$ ${\ displaystyle F (| a \ rangle \ otimes | b \ rangle) = | a + b {\ pmod {2 ^ {n}}} \ rangle \ otimes | a \ rangle}$ ${\ displaystyle a + b}$ ${\ displaystyle a}$ ${\ displaystyle a}$ ${\ displaystyle (a + b) -a = b}$

Todas as expressões algébricas booleanas podem ser codificadas como transformadas unitárias (portas lógicas quânticas), por exemplo, usando combinações das portas Pauli-X , CNOT e Toffoli . Essas portas são funcionalmente completas no domínio da lógica booleana.

Existem muitas transformações unitárias disponíveis nas bibliotecas de Q # , QCL , Qiskit e outras linguagens de programação quântica . Também aparece na literatura.

Por exemplo, onde é o número de qubits que constituem o registro , é implementado da seguinte forma em QCL: ${\ displaystyle \ mathrm {inc} (| x \ rangle) = | x + 1 {\ pmod {2 ^ {x _ {\ text {length}}}}} \ rangle}$ ${\ displaystyle x _ {\ text {length}}}$ ${\ displaystyle x}$

O circuito gerado, quando . Os símbolos , e denotam XOR , AND e NOT respectivamente, e vêm da representação booleana de Pauli- X com zero ou mais qubits de controle quando aplicados a estados que estão na base computacional.

{\ displaystyle x _ {\ text {length}} = 4}

{\ displaystyle \ oplus}

{\ displaystyle \ land}

{\ displaystyle \ neg}

cond qufunct inc(qureg x) { // increment register
  int i;
  for i = #x-1 to 0 step -1 {
    CNot(x[i], x[0::i]);     // apply controlled-not from
  }                          // MSB to LSB
}

Em QCL, o decremento é feito "desfazendo" o incremento. O prefixo !é usado para executar o inverso unitário da função. !inc(x)é o inverso de inc(x)e, em vez disso, realiza a operação . A palavra-chave significa que a função pode ser condicional . ${\ displaystyle \ mathrm {inc} ^ {\ dagger} | x \ rangle = \ mathrm {inc} ^ {- 1} (| x \ rangle) = | x-1 {\ pmod {2 ^ {x _ {\ text {comprimento}}}}} \ rangle}$ cond

No modelo de computação usado neste artigo (o modelo de circuito quântico ), um computador clássico gera a composição de porta para o computador quântico, e o computador quântico se comporta como um coprocessador que recebe instruções do computador clássico sobre quais portas primitivas aplicar. que qubits. A medição dos registros quânticos resulta em valores binários que o computador clássico pode usar em seus cálculos. Os algoritmos quânticos geralmente contêm uma parte clássica e uma parte quântica. E / S não medida (enviando qubits para computadores remotos sem colapsar seus estados quânticos) pode ser usada para criar redes de computadores quânticos . A troca de entrelaçamento pode então ser usada para realizar algoritmos distribuídos com computadores quânticos que não estão diretamente conectados. Exemplos de algoritmos distribuídos que requerem apenas o uso de um punhado de portas lógicas quânticas são a codificação superdensa , o acordo bizantino quântico e o protocolo de troca de chaves de criptografia BB84 .

Veja também

Cálculo quântico adiabático
Autômato celular e autômato celular quântico
Computação clássica e computação quântica
Porta lógica clássica , conectiva lógica e lógica quântica
Computação quântica baseada em nuvem
Teoria da complexidade computacional e BQP
Definição contrafactual e computação contrafactual
Critérios de DiVincenzo e volume quântico
Princípio de Landauer e computação reversível , decoerência
Formulação matemática da mecânica quântica
Teoria da informação , informação quântica e entropia de Von Neumann
Efeito Pauli e Sincronicidade
Matrizes de Pauli
Algoritmos quânticos
Circuito quântico
Correção de erro quântico
Autômatos finitos quânticos
Teletransporte de portal quântico
Memória quântica
Rede quântica e canal quântico
Estado quântico , matriz de densidade e Qubit
U (2 ^q ) e SU (2 ^q ) onde é o número de qubits sobre os quais as portas atuam ${\ displaystyle q}$
Transformações unitárias em mecânica quântica
Efeito zeno

Notas

Referências

^ ^a ^b ^c ^d ^e ^f Colin P. Williams (2011). Explorations in Quantum Computing . Springer . ISBN 978-1-84628-887-6.
^ ^a ^b Feynman, Richard P. (1986). "Computadores mecânicos quânticos". Fundamentos da Física . Springer Science and Business Media LLC. 16 (6): 507–531. doi : 10.1007 / bf01886518 . ISSN 0015-9018 .
^ ^a ^b ^c ^d ^e Barenco, Adriano; Bennett, Charles H .; Cleve, Richard; DiVincenzo, David P .; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A .; Weinfurter, Harald (01/11/1995). "Portas elementares para computação quântica". Physical Review A . American Physical Society (APS). 52 (5): 3457–3467. arXiv : quant-ph / 9503016 . doi : 10.1103 / physreva.52.3457 . ISSN 1050-2947 .
^ ^a ^b ^c ^d ^e ^f Nielsen, Michael A .; Chuang, Isaac (2010). Computação quântica e informação quântica . Cambridge: Cambridge University Press . ISBN 978-1-10700-217-3. OCLC 43641333 .
^ Preskill, John (2021-06-06). "Computação quântica 40 anos depois". pp. 10–15. arXiv : 2106,10522 [ quant-ph ].
^ ^a ^b ^c Yanofsky, Noson S .; Mannucci, Mirco (2013). Computação quântica para cientistas da computação . Cambridge University Press . ISBN 978-0-521-87996-5.
^ "Biblioteca de circuitos" . IBM (Qiskit).
^ "cQASM: operações de porta Qubit" . QuTech.
^ "Namespace Microsoft.Quantum.Intrinsic" . Microsoft (Q #).
^ ^a ^b Operações e funções (documentação Q #)
^ ^a ^b Ömer, Bernhard (2 de setembro de 2009). "Programação Quântica Estruturada" (PDF) . Instituto de Física Teórica, Universidade de Tecnologia de Viena: 72, 92–107. Citar diário requer |journal=( ajuda )
^ ^a ^b Ömer, Bernhard (29 de abril de 2003). "Conceitos clássicos em programação quântica". arXiv : quant-ph / 0211100 . doi : 10.1007 / s10773-005-7071-x . Citar diário requer |journal=( ajuda )
^ Dibyendu Chatterjee, Arijit Roy (2015). "Um esquema de meio somador quântico baseado em transmon" . Progresso da Física Teórica e Experimental . 2015 (9): 7–8. Bibcode : 2015PTEP.2015i3A02C . doi : 10.1093 / ptep / ptv122 .
^ David C. McKay, Christopher J. Wood, Sarah Sheldon, Jerry M. Chow, Jay M. Gambetta (31 de agosto de 2017). "Portas Z eficientes para computação quântica". Physical Review A . 96 (2). arXiv : 1612,00858 . doi : 10.1093 / ptep / ptv122 .CS1 maint: usa o parâmetro de autores ( link )
^ "qiskit.circuit.library.PhaseGate" . IBM (documentação qiskit).
^ Griffiths, DJ (2008). Introdução às Partículas Elementares (2ª ed.) . John Wiley & Sons . pp. 127–128. ISBN 978-3-527-40601-2.
^ Nemirovsky, Jonathan; Sagi, Yoav (2021), "Fast universal two-qubit gate for neutral fermionic atoms in óptico tweezers" , Physical Review Research , 3 (1): 013113, arXiv : 2008.09819 , Bibcode : 2021PhRvR ... 3a3113N , doi : 10.1103 / PhysRevResearch.3.013113
^ ^a ^b Williams, Colin P. (2011), Williams, Colin P. (ed.), "Quantum Gates" , Explorations in Quantum Computing , Texts in Computer Science, Londres: Springer, pp. 51-122, doi : 10.1007 / 978-1-84628-887-6_2 , ISBN 978-1-84628-887-6, recuperado em 2021-05-14
^ Aharonov, Dorit (2003-01-09). "Uma prova simples de que Toffoli e Hadamard são Quantum Universal". arXiv : quant-ph / 0301040 .
^ "Conferência Monroe" (PDF) . online.kitp.ucsb.edu .
^ "Demonstração de um pequeno computador quântico programável com qubits atômicos" (PDF) . Recuperado em 10/02/2019 .
^ Jones, Jonathan A. (2003). "Portas de Ising robustas para computação quântica prática". Physical Review A . 67 (1): 012317. arXiv : quant-ph / 0209049 . Bibcode : 2003PhRvA..67a2317J . doi : 10.1103 / PhysRevA.67.012317 . S2CID 119421647 .
^ Rasmussen, SE; Zinner, NT (2020-07-17). "Implementação simples de portas de troca controladas de alta fidelidade e exponenciação de circuitos quânticos de portas não Hermitianas" . Pesquisa de revisão física . 2 (3): 033097. arXiv : 2002.11728 . Bibcode : 2020PhRvR ... 2c3097R . doi : 10.1103 / PhysRevResearch.2.033097 . ISSN 2643-1564 .
^ Schuch, Norbert; Siewert, Jens (2003-03-10). "Portão natural de dois qubit para computação quântica usando a interação XY" . Physical Review A . 67 (3): 032301. arXiv : quant-ph / 0209035 . Bibcode : 2003PhRvA..67c2301S . doi : 10.1103 / PhysRevA.67.032301 . ISSN 1050-2947 .
^ Dallaire-Demers, Pierre-Luc; Wilhelm, Frank K. (05-12-2016). "Portas quânticas e arquitetura para a simulação quântica do modelo de Fermi-Hubbard" . Physical Review A . 94 (6): 062304. arXiv : 1606,00208 . Bibcode : 2016PhRvA..94f2304D . doi : 10.1103 / PhysRevA.94.062304 . ISSN 2469-9926 .
^ Shi, Xiao-Feng (22/05/2018). "Deutsch, Toffoli e cnot Gates via Rydberg Blockade of Neutral Atoms" . Revisão física aplicada . 9 (5): 051001. arXiv : 1710.01859 . Bibcode : 2018PhRvP ... 9e1001S . doi : 10.1103 / PhysRevApplied.9.051001 . ISSN 2331-7019 .
^ Aharonov, Dorit (2003-01-09). "Uma prova simples de que Toffoli e Hadamard são Quantum Universal". arXiv : quant-ph / 0301040 .
^ Deutsch, David (8 de setembro de 1989), "Quantum computational networks", Proc. R. Soc. Lond. A , 425 (1989): 73–90, Bibcode : 1989RSPSA.425 ... 73D , doi : 10.1098 / rspa.1989.0099 , S2CID 123073680
^ Bausch, Johannes; Piddock, Stephen (2017), "The Complexity of Translationally-Invariant Low-Dimensional Spin Lattices in 3D", Journal of Mathematical Physics , 58 (11): 111901, arXiv : 1702.08830 , Bibcode : 2017JMP .... 58k1901B , doi : 10.1063 / 1.5011338 , S2CID 8502985
^ Raz, Ran (2002). “Sobre a complexidade do produto matricial”. Anais do trigésimo quarto Simpósio Anual da ACM em Teoria da Computação : 144. doi : 10.1145 / 509907.509932 . ISBN 1581134959. S2CID 9582328 .
^ ^a ^b ^c Ömer, Bernhard (2000-01-20). Programação Quântica em QCL (PDF) (Tese). Instituto de Física Teórica, Universidade de Tecnologia de Viena . Página visitada em 2021-05-24 .
^ Griffiths, DJ (2008). Introdução às Partículas Elementares (2ª ed.) . John Wiley & Sons . pp. 115-121, 126. ISBN 978-3-527-40601-2.
^ David Albert (1994). Mecânica quântica e experiência . Harvard University Press . p. 35. ISBN 0-674-74113-7.
^ Sean M. Carroll (2019). Espaço-tempo e geometria: uma introdução à relatividade geral . Cambridge University Press . pp. 376–394. ISBN 978-1-108-48839-6.
^ David Wallace (2012). O multiverso emergente: teoria quântica de acordo com a interpretação de Everett . Oxford University Press . ISBN 9780199546961.
^ Sean M. Carroll (2019). Algo profundamente escondido: mundos quânticos e o surgimento do espaço-tempo . Penguin Random House . ISBN 9781524743017.
^ Q # Manual online: medição
^ Juan Yin, Yuan Cao, Yu-Huai Li, etc. (2017). "Distribuição de emaranhamento baseada em satélite por mais de 1200 quilômetros" . Quantum Optics . 356 : 1140–1144. arXiv : 1707.01339 .CS1 maint: usa o parâmetro de autores ( link )
^ Billings, Lee. "China quebra" recorde assustador de ação à distância, Preps for Quantum Internet " . Scientific American .
^ Popkin, Gabriel (15 de junho de 2017). "O satélite quântico da China atinge uma 'ação assustadora' a uma distância recorde" . Ciência - AAAS .
^ Dawson, Christopher M .; Nielsen, Michael (01-01-2006). "O algoritmo Solovay-Kitaev" . Informação e computação quântica . 6 (1). Seção 5.1, equação 23. arXiv : quant-ph / 0505030 . doi : 10.26421 / QIC6.1-6 .
^ Matteo, Olivia Di (2016). "Paralelizando a síntese do circuito quântico" . Ciência e tecnologia quântica . 1 (1): 015003. arXiv : 1606.07413 . Bibcode : 2016QS & T .... 1a5003D . doi : 10.1088 / 2058-9565 / 1/1/015003 . S2CID 62819073 .
^ Aaronson, Scott (2002). "Limite inferior quântico para amostragem recursiva de Fourier". Informação e computação quântica . 3 (2): 165–174. arXiv : quant-ph / 0209060 . Bibcode : 2002quant.ph..9060A . doi : 10.26421 / QIC3.2-7 .
^ Q # manual online: Quantum Memory Management
^ Ryo, Asaka; Kazumitsu, Sakai; Ryoko, Yahagi (2020). "Circuito quântico para a transformada rápida de Fourier" . Processamento de informações quânticas . 19 (277): 277. arXiv : 1911.03055 . Bibcode : 2020QuIP ... 19..277A . doi : 10.1007 / s11128-020-02776-5 . S2CID 207847474 .
^ Montaser, Rasha (2019). "Novo projeto de Full Adder / Subtractor reversível usando a porta R". International Journal of Theoretical Physics . 58 (1): 167–183. arXiv : 1708,00306 . Bibcode : 2019IJTP ... 58..167M . doi : 10.1007 / s10773-018-3921-1 . S2CID 24590164 .
^ Código-fonte QCL 0.6.4, o arquivo "lib / examples.qcl"
^ SJ Pauka, K. Das, R. Kalra, A. Moini, Y. Yang, M. Instrutor, A. Bousquet, C. Cantaloube, N. Dick, GC Gardner, MJ (2021). "Um chip CMOS criogênico para gerar sinais de controle para vários qubits" . Nature Electronics . 4 (4): 64–70. arXiv : 1912.01299 . doi : 10.1038 / s41928-020-00528-y .CS1 maint: usa o parâmetro de autores ( link )

Fontes

Nielsen, Michael A .; Chuang, Isaac (2000). Computação quântica e informação quântica . Cambridge: Cambridge University Press . ISBN 0521632358. OCLC 43641333 .
Colin P. Williams (2011). Explorations in Quantum Computing . Springer . ISBN 978-1-84628-887-6.
Yanofsky, Noson S .; Mannucci, Mirco (2013). Computação quântica para cientistas da computação . Cambridge University Press . ISBN 978-0-521-87996-5.

[Williams-1] ^ ^a ^b ^c ^d ^e ^f Colin P. Williams (2011). Explorations in Quantum Computing . Springer . ISBN 978-1-84628-887-6.

[Feynman-QMC-2] Feynman, Richard P. (1986). "Computadores mecânicos quânticos". Fundamentos da Física . Springer Science and Business Media LLC. 16 (6): 507–531. doi : 10.1007 / bf01886518 . ISSN 0015-9018 .

[Barenco-3] Barenco, Adriano; Bennett, Charles H .; Cleve, Richard; DiVincenzo, David P .; Margolus, Norman; Shor, Peter; Sleator, Tycho; Smolin, John A .; Weinfurter, Harald (01/11/1995). "Portas elementares para computação quântica". Physical Review A . American Physical Society (APS). 52 (5): 3457–3467. arXiv : quant-ph / 9503016 . doi : 10.1103 / physreva.52.3457 . ISSN 1050-2947 .

[Nielsen-Chuang-5] ^ ^a ^b ^c ^d ^e ^f Nielsen, Michael A .; Chuang, Isaac (2010). Computação quântica e informação quântica . Cambridge: Cambridge University Press . ISBN 978-1-10700-217-3. OCLC 43641333 .

[Preskill-6] Preskill, John (2021-06-06). "Computação quântica 40 anos depois". pp. 10–15. arXiv : 2106,10522 [ quant-ph ].

[Yanofsky-Mannucci-7] Yanofsky, Noson S .; Mannucci, Mirco (2013). Computação quântica para cientistas da computação . Cambridge University Press . ISBN 978-0-521-87996-5.

[8] "Biblioteca de circuitos" . IBM (Qiskit).

[inspire-9] "cQASM: operações de porta Qubit" . QuTech.

[10] "Namespace Microsoft.Quantum.Intrinsic" . Microsoft (Q #).

[adjoint-controlled-qsharp-11] Operações e funções (documentação Q #)

[Oemer-structured-programming-12] Ömer, Bernhard (2 de setembro de 2009). "Programação Quântica Estruturada" (PDF) . Instituto de Física Teórica, Universidade de Tecnologia de Viena: 72, 92–107. Citar diário requer |journal=( ajuda )

[Oemer2-13] Ömer, Bernhard (29 de abril de 2003). "Conceitos clássicos em programação quântica". arXiv : quant-ph / 0211100 . doi : 10.1007 / s10773-005-7071-x . Citar diário requer |journal=( ajuda )

[18] Dibyendu Chatterjee, Arijit Roy (2015). "Um esquema de meio somador quântico baseado em transmon" . Progresso da Física Teórica e Experimental . 2015 (9): 7–8. Bibcode : 2015PTEP.2015i3A02C . doi : 10.1093 / ptep / ptv122 .

[19] David C. McKay, Christopher J. Wood, Sarah Sheldon, Jerry M. Chow, Jay M. Gambetta (31 de agosto de 2017). "Portas Z eficientes para computação quântica". Physical Review A . 96 (2). arXiv : 1612,00858 . doi : 10.1093 / ptep / ptv122 .CS1 maint: usa o parâmetro de autores ( link )

[20] "qiskit.circuit.library.PhaseGate" . IBM (documentação qiskit).

[21] Griffiths, DJ (2008). Introdução às Partículas Elementares (2ª ed.) . John Wiley & Sons . pp. 127–128. ISBN 978-3-527-40601-2.

[22] Nemirovsky, Jonathan; Sagi, Yoav (2021), "Fast universal two-qubit gate for neutral fermionic atoms in óptico tweezers" , Physical Review Research , 3 (1): 013113, arXiv : 2008.09819 , Bibcode : 2021PhRvR ... 3a3113N , doi : 10.1103 / PhysRevResearch.3.013113

[:0-23] Williams, Colin P. (2011), Williams, Colin P. (ed.), "Quantum Gates" , Explorations in Quantum Computing , Texts in Computer Science, Londres: Springer, pp. 51-122, doi : 10.1007 / 978-1-84628-887-6_2 , ISBN 978-1-84628-887-6, recuperado em 2021-05-14

[24] Aharonov, Dorit (2003-01-09). "Uma prova simples de que Toffoli e Hadamard são Quantum Universal". arXiv : quant-ph / 0301040 .

[25] "Conferência Monroe" (PDF) . online.kitp.ucsb.edu .

[monroe2012-26] "Demonstração de um pequeno computador quântico programável com qubits atômicos" (PDF) . Recuperado em 10/02/2019 .

[27] Jones, Jonathan A. (2003). "Portas de Ising robustas para computação quântica prática". Physical Review A . 67 (1): 012317. arXiv : quant-ph / 0209049 . Bibcode : 2003PhRvA..67a2317J . doi : 10.1103 / PhysRevA.67.012317 . S2CID 119421647 .

[28] Rasmussen, SE; Zinner, NT (2020-07-17). "Implementação simples de portas de troca controladas de alta fidelidade e exponenciação de circuitos quânticos de portas não Hermitianas" . Pesquisa de revisão física . 2 (3): 033097. arXiv : 2002.11728 . Bibcode : 2020PhRvR ... 2c3097R . doi : 10.1103 / PhysRevResearch.2.033097 . ISSN 2643-1564 .

[29] Schuch, Norbert; Siewert, Jens (2003-03-10). "Portão natural de dois qubit para computação quântica usando a interação XY" . Physical Review A . 67 (3): 032301. arXiv : quant-ph / 0209035 . Bibcode : 2003PhRvA..67c2301S . doi : 10.1103 / PhysRevA.67.032301 . ISSN 1050-2947 .

[30] Dallaire-Demers, Pierre-Luc; Wilhelm, Frank K. (05-12-2016). "Portas quânticas e arquitetura para a simulação quântica do modelo de Fermi-Hubbard" . Physical Review A . 94 (6): 062304. arXiv : 1606,00208 . Bibcode : 2016PhRvA..94f2304D . doi : 10.1103 / PhysRevA.94.062304 . ISSN 2469-9926 .

[31] Shi, Xiao-Feng (22/05/2018). "Deutsch, Toffoli e cnot Gates via Rydberg Blockade of Neutral Atoms" . Revisão física aplicada . 9 (5): 051001. arXiv : 1710.01859 . Bibcode : 2018PhRvP ... 9e1001S . doi : 10.1103 / PhysRevApplied.9.051001 . ISSN 2331-7019 .

[32] Aharonov, Dorit (2003-01-09). "Uma prova simples de que Toffoli e Hadamard são Quantum Universal". arXiv : quant-ph / 0301040 .

[33] Deutsch, David (8 de setembro de 1989), "Quantum computational networks", Proc. R. Soc. Lond. A , 425 (1989): 73–90, Bibcode : 1989RSPSA.425 ... 73D , doi : 10.1098 / rspa.1989.0099 , S2CID 123073680

[34] Bausch, Johannes; Piddock, Stephen (2017), "The Complexity of Translationally-Invariant Low-Dimensional Spin Lattices in 3D", Journal of Mathematical Physics , 58 (11): 111901, arXiv : 1702.08830 , Bibcode : 2017JMP .... 58k1901B , doi : 10.1063 / 1.5011338 , S2CID 8502985

[36] Raz, Ran (2002). “Sobre a complexidade do produto matricial”. Anais do trigésimo quarto Simpósio Anual da ACM em Teoria da Computação : 144. doi : 10.1145 / 509907.509932 . ISBN 1581134959. S2CID 9582328 .

[Oemer-37] Ömer, Bernhard (2000-01-20). Programação Quântica em QCL (PDF) (Tese). Instituto de Física Teórica, Universidade de Tecnologia de Viena . Página visitada em 2021-05-24 .

[38] Griffiths, DJ (2008). Introdução às Partículas Elementares (2ª ed.) . John Wiley & Sons . pp. 115-121, 126. ISBN 978-3-527-40601-2.

[39] David Albert (1994). Mecânica quântica e experiência . Harvard University Press . p. 35. ISBN 0-674-74113-7.

[40] Sean M. Carroll (2019). Espaço-tempo e geometria: uma introdução à relatividade geral . Cambridge University Press . pp. 376–394. ISBN 978-1-108-48839-6.

[41] David Wallace (2012). O multiverso emergente: teoria quântica de acordo com a interpretação de Everett . Oxford University Press . ISBN 9780199546961.

[42] Sean M. Carroll (2019). Algo profundamente escondido: mundos quânticos e o surgimento do espaço-tempo . Penguin Random House . ISBN 9781524743017.

[44] Q # Manual online: medição

[45] Juan Yin, Yuan Cao, Yu-Huai Li, etc. (2017). "Distribuição de emaranhamento baseada em satélite por mais de 1200 quilômetros" . Quantum Optics . 356 : 1140–1144. arXiv : 1707.01339 .CS1 maint: usa o parâmetro de autores ( link )

[46] Billings, Lee. "China quebra" recorde assustador de ação à distância, Preps for Quantum Internet " . Scientific American .

[47] Popkin, Gabriel (15 de junho de 2017). "O satélite quântico da China atinge uma 'ação assustadora' a uma distância recorde" . Ciência - AAAS .

[48] Dawson, Christopher M .; Nielsen, Michael (01-01-2006). "O algoritmo Solovay-Kitaev" . Informação e computação quântica . 6 (1). Seção 5.1, equação 23. arXiv : quant-ph / 0505030 . doi : 10.26421 / QIC6.1-6 .

[49] Matteo, Olivia Di (2016). "Paralelizando a síntese do circuito quântico" . Ciência e tecnologia quântica . 1 (1): 015003. arXiv : 1606.07413 . Bibcode : 2016QS & T .... 1a5003D . doi : 10.1088 / 2058-9565 / 1/1/015003 . S2CID 62819073 .

[50] Aaronson, Scott (2002). "Limite inferior quântico para amostragem recursiva de Fourier". Informação e computação quântica . 3 (2): 165–174. arXiv : quant-ph / 0209060 . Bibcode : 2002quant.ph..9060A . doi : 10.26421 / QIC3.2-7 .

[51] Q # manual online: Quantum Memory Management

[53] Ryo, Asaka; Kazumitsu, Sakai; Ryoko, Yahagi (2020). "Circuito quântico para a transformada rápida de Fourier" . Processamento de informações quânticas . 19 (277): 277. arXiv : 1911.03055 . Bibcode : 2020QuIP ... 19..277A . doi : 10.1007 / s11128-020-02776-5 . S2CID 207847474 .

[54] Montaser, Rasha (2019). "Novo projeto de Full Adder / Subtractor reversível usando a porta R". International Journal of Theoretical Physics . 58 (1): 167–183. arXiv : 1708,00306 . Bibcode : 2019IJTP ... 58..167M . doi : 10.1007 / s10773-018-3921-1 . S2CID 24590164 .

[55] Código-fonte QCL 0.6.4, o arquivo "lib / examples.qcl"

[56] SJ Pauka, K. Das, R. Kalra, A. Moini, Y. Yang, M. Instrutor, A. Bousquet, C. Cantaloube, N. Dick, GC Gardner, MJ (2021). "Um chip CMOS criogênico para gerar sinais de controle para vários qubits" . Nature Electronics . 4 (4): 64–70. arXiv : 1912.01299 . doi : 10.1038 / s41928-020-00528-y .CS1 maint: usa o parâmetro de autores ( link )

Languages

In other projects