Coordenadas de Rindler - Rindler coordinates

Na física relativística , as coordenadas de um referencial hiperbolicamente acelerado constituem um gráfico de coordenadas importante e útil que representa parte do espaço-tempo plano de Minkowski . Na relatividade especial , uma partícula em aceleração uniforme sofre movimento hiperbólico , para o qual um referencial de aceleração uniforme no qual ela está em repouso pode ser escolhido como seu referencial apropriado . Os fenômenos neste quadro hiperbolicamente acelerado podem ser comparados aos efeitos que surgem em um campo gravitacional homogêneo . Para uma visão geral das acelerações no espaço-tempo plano, consulte Aceleração (relatividade especial) e referencial apropriado (espaço-tempo plano) .

Neste artigo, a velocidade da luz é definida por c = 1 , as coordenadas inerciais são ( X , Y , Z , T ) e as coordenadas hiperbólicas são ( x , y , z , t ) . Essas coordenadas hiperbólicas podem ser separadas em duas variantes principais, dependendo da posição do observador acelerado: Se o observador estiver localizado no tempo T = 0 na posição X = 1 / α (com α como a aceleração adequada constante medida por um acelerômetro em movimento ), então as coordenadas hiperbólicas são freqüentemente chamadas de coordenadas de Rindler com a métrica de Rindler correspondente . Se o observador está localizado no tempo T = 0 na posição X = 0 , então as coordenadas hiperbólicas são algumas vezes chamadas de coordenadas de Møller ou coordenadas de Kottler-Møller com a métrica Kottler-Møller correspondente . Um gráfico alternativo frequentemente relacionado a observadores em movimento hiperbólico é obtido usando coordenadas de radar, às vezes chamadas de coordenadas de Lass . Ambas as coordenadas de Kottler-Møller, bem como as coordenadas de Lass, também são indicadas como coordenadas de Rindler.

Em relação à história, tais coordenadas foram introduzidas logo após o advento da relatividade especial, quando foram estudadas (total ou parcialmente) ao lado do conceito de movimento hiperbólico: Em relação ao espaço-tempo plano de Minkowski por Albert Einstein (1907, 1912), Max Born ( 1909), Arnold Sommerfeld (1910), Max von Laue (1911), Hendrik Lorentz (1913), Friedrich Kottler (1914), Wolfgang Pauli (1921), Karl Bollert (1922), Stjepan Mohorovičić (1922), Georges Lemaître (1924) ), Einstein & Nathan Rosen (1935), Christian Møller (1943, 1952), Fritz Rohrlich (1963), Harry Lass (1963) e em relação ao espaço-tempo plano e curvo da relatividade geral por Wolfgang Rindler (1960, 1966) . Para obter detalhes e fontes, consulte § Histórico .

Características do quadro Rindler

Gráfico de Rindler, para na equação ( 1a ), traçado em um diagrama de Minkowski. As linhas tracejadas são os horizontes Rindler${\ displaystyle \ alpha = 0,5}$

A linha de mundo de um corpo em movimento hiperbólico com aceleração adequada constante na direção em função do tempo e rapidez adequados pode ser dada por ${\ displaystyle \ alpha}$${\ displaystyle X}$ ${\ displaystyle \ tau}$ ${\ displaystyle \ alpha \ tau}$

${\ displaystyle T = x \ sinh (\ alpha \ tau), \ quad X = x \ cosh (\ alpha \ tau)}$

onde é constante e é variável, com a linha do mundo se assemelhando à hipérbole . Sommerfeld mostrou que as equações podem ser reinterpretadas definindo-as como variáveis ​​e constantes, de modo que representem a "forma de repouso" simultânea de um corpo em movimento hiperbólico medido por um observador em movimento. Ao usar o tempo adequado do observador como o tempo de todo o quadro hiperbolicamente acelerado por configuração , as fórmulas de transformação entre as coordenadas inerciais e as coordenadas hiperbólicas são, conseqüentemente: ${\ displaystyle x = 1 / \ alpha}$${\ displaystyle \ alpha \ tau}$${\ displaystyle X ^ {2} -T ^ {2} = x ^ {2}}$${\ displaystyle x}$${\ displaystyle \ alpha \ tau}$${\ displaystyle \ tau = t}$

${\ displaystyle T = x \ sinh (\ alpha t), \ quad X = x \ cosh (\ alpha t), \ quad Y = y, \ quad Z = z}$

( 1a )

com o inverso

${\ displaystyle t = {\ frac {1} {\ alpha}} \ operatorname {artanh} \ left ({\ frac {T} {X}} \ right), \ quad x = {\ sqrt {X ^ {2 } -T ^ {2}}}, \ quad y = Y, \ quad z = Z}$

Diferenciada e inserida na métrica de Minkowski , a métrica no quadro hiperbolicamente acelerado segue ${\ displaystyle ds ^ {2} = - dT ^ {2} + dX ^ {2} + dY ^ {2} + dZ ^ {2}}$

${\ displaystyle ds ^ {2} = - (\ alpha x) ^ {2} dt ^ {2} + dx ^ {2} + dy ^ {2} + dz ^ {2}}$

( 1b )

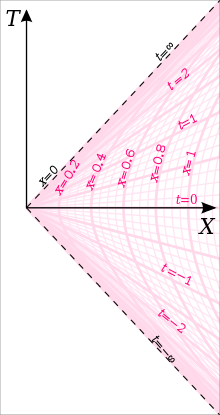
Essas transformações definem o observador Rindler como um observador que está "em repouso" nas coordenadas de Rindler, ou seja, mantendo x , y , z constantes e apenas variando t com o passar do tempo. As coordenadas são válidas na região , que muitas vezes é chamada de cunha de Rindler , se representa a própria aceleração (ao longo da hipérbole ) do observador de Rindler cujo tempo próprio é definido como igual ao tempo das coordenadas de Rindler. Para manter esta linha de mundo, o observador deve acelerar com uma aceleração adequada constante, com os observadores Rindler mais próximos (do horizonte de Rindler ) tendo uma aceleração adequada maior. Todos os observadores Rindler estão instantaneamente em repouso no tempo no referencial inercial, e neste momento um observador Rindler com aceleração adequada estará na posição (realmente , mas assumimos unidades onde ), que também é a distância constante desse observador do horizonte de Rindler em coordenadas de Rindler. Se todos os observadores Rindler definirem seus relógios para zero em , então, ao definir um sistema de coordenadas Rindler, temos uma escolha de qual tempo adequado do observador Rindler será igual ao tempo de coordenada nas coordenadas de Rindler, e a aceleração adequada deste observador define o valor de acima ( para outros observadores Rindler em distâncias diferentes do horizonte de Rindler, o tempo coordenado será igual a algum múltiplo constante de seu próprio tempo). É uma convenção comum definir o sistema de coordenadas de Rindler de forma que o observador Rindler cujo tempo apropriado coincide com o tempo de coordenada seja aquele que tem aceleração adequada , de forma que possa ser eliminado das equações. ${\ displaystyle 0 <X <\ infty, \; - X <T <X}$${\ displaystyle \ alpha}$${\ displaystyle x = 1 / \ alpha}$${\ displaystyle x = 0}$${\ displaystyle T = 0}$${\ displaystyle \ alpha _ {i}}$${\ displaystyle X = 1 / \ alpha _ {i}}$${\ displaystyle X = c ^ {2} / \ alpha _ {i}}$${\ displaystyle c = 1}$${\ displaystyle T = 0}$${\ displaystyle t}$${\ displaystyle \ alpha}$${\ displaystyle \ alpha = 1}$${\ displaystyle \ alpha}$

A equação acima foi simplificada para . A equação não simplificada é mais conveniente para encontrar a distância do horizonte de Rindler, dada uma aceleração . ${\ displaystyle c = 1}$${\ displaystyle \ alpha}$

${\ displaystyle {\ begin {alinhados} t & = {\ frac {c} {\ alpha}} \ operatorname {artanh} \ left ({\ frac {cT} {X}} \ right) \; {\ overset {X \, \ gg \, cT} {\ approx}} \; {\ frac {c ^ {2} T} {\ alpha X}} \\ X & \ approx {\ frac {c ^ {2} T} {\ alpha t}} \; {\ overset {T \, \ approx \, t} {\ approx}} \; {\ frac {c ^ {2}} {\ alpha}} \ end {alinhado}}}$

O restante do artigo seguirá a convenção de definir as unidades e , portanto, as unidades para e serão 1 unidade . Lembre-se de que definir segundo / segundo-luz ² é muito diferente de definir ano-luz / ano ² . Mesmo se escolhermos unidades onde , a magnitude da aceleração adequada dependerá de nossa escolha de unidades: por exemplo, se usarmos unidades de anos-luz para distância, ( ou ) e anos para tempo, ( ou ), isso significaria ano-luz / ano ² , igual a cerca de 9,5 metros / segundo ² , enquanto se usarmos unidades de segundos-luz para distância, ( ou ) e segundos para tempo, ( ou ), isso significaria segundos-luz / segundo ² , ou 299 792 458 metros / segundo ² ). ${\ displaystyle \ alpha = 1}$${\ displaystyle c = 1}$${\ displaystyle X}$${\ displaystyle x}$${\ displaystyle = c ^ {2} / \ alpha = 1}$${\ displaystyle \ alpha = 1}$${\ displaystyle \ alpha = 1}$${\ displaystyle c = 1}$${\ displaystyle \ alpha}$${\ displaystyle X}$${\ displaystyle x}$${\ displaystyle T}$${\ displaystyle t}$${\ displaystyle \ alpha = 1}$${\ displaystyle X}$${\ displaystyle x}$${\ displaystyle T}$${\ displaystyle t}$${\ displaystyle \ alpha = 1}$

Variantes de fórmulas de transformação

Uma derivação mais geral das fórmulas de transformação é dada, quando a tétrade de Fermi-Walker correspondente é formulada a partir da qual as coordenadas de Fermi ou coordenadas Próprias podem ser derivadas. Dependendo da escolha da origem dessas coordenadas, pode-se derivar a métrica, a dilatação do tempo entre o tempo na origem e no ponto , e a velocidade da luz coordenada (esta velocidade variável da luz não contradiz a relatividade especial, porque é apenas um artefato das coordenadas aceleradas empregadas, enquanto nas coordenadas inerciais ele permanece constante). Em vez de coordenadas de Fermi, também podem ser usadas as coordenadas de radar, que são obtidas através da determinação da distância usando sinais de luz (ver seção Noções de distância ), em que métrica, dilatação do tempo e velocidade da luz não dependem mais das coordenadas - em particular , a velocidade coordenada da luz permanece idêntica à velocidade da luz em quadros inerciais: ${\ displaystyle dt_ {0}}$${\ displaystyle dt}$${\ displaystyle x}$${\ displaystyle | dx | / | dt |}$${\ displaystyle (c = 1)}$

${\ displaystyle X}$ no ${\ displaystyle T = 0}$	Transformação, métrica, dilatação do tempo e velocidade coordenada da luz
${\ displaystyle X = 0}$	Coordenadas Kottler-Møller
	${\ displaystyle {\ begin {array} {c | c} {\ begin {alinhado} T & = \ left (x + {\ frac {1} {\ alpha}} \ right) \ sinh (\ alpha t) \\ X & = \ left (x + {\ frac {1} {\ alpha}} \ right) \ cosh (\ alpha t) - {\ frac {1} {\ alpha}} \\ Y & = y \\ Z & = z \ end {alinhados}} & {\ begin {alinhados} t & = {\ frac {1} {\ alpha}} \ operatorname {artanh} \ left ({\ frac {T} {X + {\ frac {1} {\ alpha} }}} \ right) \\ x & = {\ sqrt {\ left (X + {\ frac {1} {\ alpha}} \ right) ^ {2} -T ^ {2}}} - {\ frac {1 } {\ alpha}} \\ y & = Y \\ z & = Z \ end {alinhado}} \ end {array}}}$ ( 2a ) ${\ displaystyle ds ^ {2} = - (1+ \ alpha x) {} ^ {2} dt ^ {2} + dx ^ {2} + dy ^ {2} + dz ^ {2}}$ ( 2b ) ${\ displaystyle dt = (1+ \ alpha x) dt_ {0}, \ qquad {\ frac {| dx |} {| dt |}} = 1+ \ alpha x}$ ( 2c )
	Coordenadas de Rindler
${\ displaystyle X = {\ frac {1} {\ alpha}}}$	${\ displaystyle {\ begin {array} {c | c} {\ begin {alinhado} T & = x \ sinh (\ alpha t) \\ X & = x \ cosh (\ alpha t) \\ Y & = y \\ Z & = z \ end {alinhados}} & {\ begin {alinhados} t & = {\ frac {1} {\ alpha}} \ operatorname {artanh} {\ frac {T} {X}} \\ x & = {\ sqrt {X ^ {2} -T ^ {2}}} \\ y & = Y \\ z & = Z \ end {alinhado}} \ end {array}}}$ ( 2d ) ${\ displaystyle ds ^ {2} = - (\ alpha x) ^ {2} dt ^ {2} + dx ^ {2} + dy ^ {2} + dz ^ {2}}$ ( 2e ) ${\ displaystyle dt = \ alpha x \ dt_ {0}, \ qquad {\ frac {| dx |} {| dt |}} = \ alpha x}$ ( 2f )
	Coordenadas de radar (coordenadas Lass)
${\ displaystyle X = {\ frac {1} {\ alpha}}}$	${\ displaystyle {\ begin {array} {c | c} {\ begin {alinhados} T & = {\ frac {1} {\ alpha}} e ^ {\ alpha x} \ sinh (\ alpha t) \\ X & = {\ frac {1} {\ alpha}} e ^ {\ alpha x} \ cosh (\ alpha t) \\ Y & = y \\ Z & = z \ end {alinhado}} & {\ begin {alinhado} t & = {\ frac {1} {\ alpha}} \ operatorname {artanh} {\ frac {T} {X}} \\ x & = {\ frac {1} {2 \ alpha}} \ ln \ left [\ alpha {} ^ {2} \ left (X ^ {2} -T ^ {2} \ right) \ right] \\ y & = Y \\ z & = Z \ end {alinhado}} \ end {array}}}$ ( 2g )
	${\ displaystyle ds ^ {2} = e ^ {2 \ alpha x} \ left (-dt ^ {2} + dx ^ {2} \ right) + dy ^ {2} + dz ^ {2}}$ ( 2h ) ${\ displaystyle dt = e ^ {\ alpha x} dt_ {0}, \ qquad {\ frac {| dx |} {| dt |}} = 1}$ ( 2i )

Os observadores Rindler

No novo gráfico ( 1a ) com e , é natural pegar o campo de coframe ${\ displaystyle c = 1}$${\ displaystyle \ alpha = 1}$

${\ displaystyle d \ sigma ^ {0} = x \, dt, \; \; d \ sigma ^ {1} = dx, \; \; d \ sigma ^ {2} = dy, \; \; d \ sigma ^ {3} = dz}$

que tem o campo de quadro duplo

${\ displaystyle {\ vec {e}} _ {0} = {\ frac {1} {x}} \ parcial _ {t}, \; \; {\ vec {e}} _ {1} = \ parcial _ {x}, \; \; {\ vec {e}} _ {2} = \ parcial _ {y}, \; \; {\ vec {e}} _ {3} = \ parcial _ {z} }$

Isso define um quadro Lorentz local no espaço tangente em cada evento (na região coberta por nosso gráfico de Rindler, ou seja, a cunha de Rindler). As curvas integrais do campo vetorial unitário semelhante ao tempo fornecem uma congruência semelhante ao tempo , consistindo nas linhas do mundo de uma família de observadores chamados de observadores Rindler . No gráfico de Rindler, essas linhas mundiais aparecem como linhas de coordenadas verticais . Usando a transformação de coordenadas acima, descobrimos que elas correspondem a arcos hiperbólicos na carta cartesiana original. ${\ displaystyle {\ vec {e}} _ {0}}$${\ displaystyle x = x_ {0}, \; y = y_ {0}, \; z = z_ {0}}$

Alguns observadores Rindler representativos (arcos hiperbólicos azul marinho) representados usando a carta cartesiana. As linhas vermelhas a 45 graus da vertical representam o horizonte de Rindler; o sistema de coordenadas Rindler é definido apenas à direita deste limite.

Como acontece com qualquer congruência semelhante ao tempo em qualquer variedade Lorentziana, esta congruência tem uma decomposição cinemática (veja a equação de Raychaudhuri ). Nesse caso, a expansão e a vorticidade da congruência dos observadores Rindler desaparecem . O desaparecimento do tensor de expansão implica que cada um de nossos observadores mantenha uma distância constante de seus vizinhos . O desaparecimento do tensor de vorticidade implica que as linhas de mundo de nossos observadores não estão se torcendo; esta é uma espécie de ausência local de "turbilhão".

O vetor de aceleração de cada observador é dado pela derivada covariante

${\ displaystyle \ nabla _ {{\ vec {e}} _ {0}} {\ vec {e}} _ {0} = {\ frac {1} {x}} {\ vec {e}} _ { 1}}$

Ou seja, cada observador Rindler está acelerando na direção. Individualmente falando, cada observador está de fato acelerando com magnitude constante nesta direção, então suas linhas de mundo são os análogos Lorentzianos dos círculos, que são as curvas de curvatura de caminho constante na geometria euclidiana. ${\ displaystyle \ partial _ {x}}$

Como os observadores Rindler são livres de vorticidade , eles também são ortogonais de hipersuperfície . Os hiperslices espaciais ortogonais são ; estes aparecem como meios planos horizontais na carta de Rindler e como meios planos na carta cartesiana (veja a figura acima). Colocando no elemento linha, vemos que estes possuem a geometria euclidiana ordinária ,. Assim, as coordenadas espaciais na carta de Rindler têm uma interpretação muito simples consistente com a afirmação de que os observadores de Rindler são mutuamente estacionários. Voltaremos a essa propriedade de rigidez dos observadores Rindler um pouco mais adiante neste artigo. ${\ displaystyle t = t_ {0}}$${\ displaystyle T = X = 0}$${\ displaystyle dt = 0}$${\ displaystyle d \ sigma ^ {2} = dx ^ {2} + dy ^ {2} + dz ^ {2}, \; \ forall x> 0, \ forall y, z}$

Uma propriedade "paradoxal"

Observe que os observadores Rindler com coordenada x constante menor estão acelerando com mais dificuldade para acompanhar. Isso pode parecer surpreendente porque, na física newtoniana, os observadores que mantêm uma distância relativa constante devem compartilhar a mesma aceleração. Mas na física relativística, vemos que o ponto final posterior de uma haste que é acelerado por alguma força externa (paralela ao seu eixo de simetria) deve acelerar um pouco mais forte do que o ponto final principal, ou então ele deve quebrar. Esta é uma manifestação da contração de Lorentz . Conforme a barra acelera, sua velocidade aumenta e seu comprimento diminui. Como está ficando mais curto, a extremidade traseira deve acelerar mais forte do que a dianteira. Outra maneira de ver isso é: o back end deve atingir a mesma mudança de velocidade em um período de tempo mais curto. Isso leva a uma equação diferencial mostrando que, a alguma distância, a aceleração da extremidade posterior diverge, resultando no horizonte de Rindler .

Este fenômeno é a base de um "paradoxo" bem conhecido, o paradoxo da nave espacial de Bell . No entanto, é uma consequência simples da cinemática relativística. Uma maneira de ver isso é observar que a magnitude do vetor de aceleração é apenas a curvatura do caminho da reta mundial correspondente. Mas as linhas de mundo de nossos observadores Rindler são análogos de uma família de círculos concêntricos no plano euclidiano, então estamos simplesmente lidando com o análogo Lorentziano de um fato familiar aos patinadores de velocidade: em uma família de círculos concêntricos, os círculos internos devem se dobrar mais rápido (por unidade de comprimento de arco) do que os externos .

Observadores Minkowski

Um observador representativo de Minkowski (curva secante hiperbólica azul marinho) descrito usando o gráfico de Rindler. O horizonte Rindler é mostrado em vermelho.

Vale a pena apresentar também uma moldura alternativa, dada na carta de Minkowski pela escolha natural

${\ displaystyle {\ vec {f}} _ {0} = \ parcial _ {T}, \; {\ vec {f}} _ {1} = \ parcial _ {X}, \; {\ vec {f }} _ {2} = \ parcial _ {Y}, \; {\ vec {f}} _ {3} = \ parcial _ {Z}}$

Transformando esses campos vetoriais usando a transformação de coordenadas fornecida acima, descobrimos que no gráfico de Rindler (na cunha de Rinder) este quadro torna-se

${\ displaystyle {\ begin {align} {\ vec {f}} _ {0} & = {\ frac {1} {x}} \ cosh (t) \, \ partial _ {t} - \ sinh (t ) \, \ parcial _ {x} \\ {\ vec {f}} _ {1} & = - {\ frac {1} {x}} \ sinh (t) \, \ parcial _ {t} + \ cosh (t) \, \ parcial _ {x} \\ {\ vec {f}} _ {2} & = \ parcial _ {y}, \; {\ vec {f}} _ {3} = \ parcial _ {z} \ end {alinhado}}}$

Calculando a decomposição cinemática da congruência semelhante ao tempo definida pelo campo vetorial unitário semelhante ao tempo , descobrimos que a expansão e a vorticidade novamente desaparecem e, além disso, o vetor de aceleração desaparece ,. Em outras palavras, esta é uma congruência geodésica ; os observadores correspondentes estão em um estado de movimento inercial . No gráfico cartesiano original, esses observadores, a quem chamaremos de observadores de Minkowski , estão em repouso. ${\ displaystyle {\ vec {f}} _ {0}}$${\ displaystyle \ nabla _ {{\ vec {f}} _ {0}} {\ vec {f}} _ {0} = 0}$

No gráfico de Rindler, as linhas de mundo dos observadores de Minkowski aparecem como curvas secantes hiperbólicas assintóticas ao plano de coordenadas . Especificamente, em coordenadas de Rindler, a linha de mundo do observador Minkowski passando pelo evento é ${\ displaystyle x = 0}$${\ displaystyle t = t_ {0}, \; x = x_ {0}, \; y = y_ {0}, \; z = z_ {0}}$

${\ displaystyle {\ begin {alinhados} t & = \ operatorname {artanh} \ left ({\ frac {s} {x_ {0}}} \ right), \; - x_ {0} <s <x_ {0} \\ x & = {\ sqrt {x_ {0} ^ {2} -s ^ {2}}}, \; - x_ {0} <s <x_ {0} \\ y & = y_ {0} \\ z & = z_ {0} \ end {alinhado}}}$

onde está a hora certa deste observador Minkowski. Observe que apenas uma pequena parte de sua história é coberta pelo gráfico de Rindler. Isso mostra explicitamente por que o gráfico de Rindler não está geodésicamente completo ; geodésicas semelhantes ao tempo são executadas fora da região coberta pelo gráfico em um tempo adequado finito. Claro, já sabíamos que a carta de Rindler não pode ser geodésicamente completa, porque cobre apenas uma parte da carta cartesiana original, que é uma carta geodésicamente completa. ${\ displaystyle s}$

No caso representado na figura, e desenhamos (corretamente dimensionados e aumentados) os cones de luz em . ${\ displaystyle x_ {0} = 1}$${\ displaystyle s \ in \ left \ {- {\ frac {1} {2}}, \; 0, \; {\ frac {1} {2}} \ right \}}$

O horizonte Rindler

O gráfico de coordenadas de Rindler tem uma singularidade de coordenadas em x  = 0, onde o tensor métrico (expresso nas coordenadas de Rindler) tem determinante de desaparecimento . Isso acontece porque quando x  → 0 a aceleração dos observadores Rindler diverge. Como podemos ver na figura que ilustra a cunha de Rindler, o locus x  = 0 no gráfico de Rindler corresponde ao locus T ²  =  X ² ,  X  > 0 no gráfico cartesiano, que consiste em dois semiplanos nulos, cada um regido por uma congruência geodésica nula.

Por enquanto, simplesmente consideramos o horizonte de Rindler como o limite das coordenadas de Rindler. Se considerarmos o conjunto de observadores em aceleração que têm uma posição constante nas coordenadas de Rindler, nenhum deles pode receber sinais de luz de eventos com T  ≥  X (no diagrama, estes seriam eventos na ou à esquerda da linha T = X ao longo do qual o horizonte vermelho superior se encontra; esses observadores poderiam, no entanto, receber sinais de eventos com T  ≥  X se eles parassem sua aceleração e cruzassem esta linha eles próprios) nem poderiam jamais ter enviado sinais para eventos com T  ≤ - X (eventos em ou à esquerda da linha T = - X ao longo do qual está o horizonte vermelho inferior; esses eventos estão fora de todos os cones de luz futuros de sua linha de mundo passada). Além disso, se considerarmos os membros deste conjunto de observadores em aceleração cada vez mais perto do horizonte, no limite conforme a distância ao horizonte se aproxima de zero, a aceleração adequada constante experimentada por um observador a esta distância (que também seria o G- força experimentada por tal observador) se aproximará do infinito. Ambos os fatos também seriam verdadeiros se estivéssemos considerando um conjunto de observadores pairando fora do horizonte de eventos de um buraco negro , cada observador pairando em um raio constante nas coordenadas de Schwarzschild . Na verdade, na vizinhança próxima de um buraco negro, a geometria próxima ao horizonte de eventos pode ser descrita em coordenadas de Rindler. A radiação Hawking, no caso de um quadro de aceleração, é conhecida como radiação de Unruh . A conexão é a equivalência da aceleração com a gravitação.

Geodésica

As equações geodésicas na carta de Rindler são facilmente obtidas a partir da Lagrangiana geodésica ; eles são

${\ displaystyle {\ ddot {t}} + {\ frac {2} {x}} \, {\ dot {x}} \, {\ dot {t}} = 0, \; {\ ddot {x} } + x \, {\ dot {t}} ^ {2} = 0, \; {\ ddot {y}} = 0, \; {\ ddot {z}} = 0}$

Claro, no gráfico cartesiano original, as geodésicas aparecem como linhas retas, então poderíamos obtê-las facilmente no gráfico de Rindler usando nossa transformação de coordenadas. No entanto, é instrutivo obtê-los e estudá-los independentemente do gráfico original, e faremos isso nesta seção.

Algumas geodésicas nulas representativas (arcos semicirculares hiperbólicos pretos) projetadas no hiperslice espacial t  = 0 dos observadores Rindler. O horizonte de Rindler é mostrado como um plano magenta.

Do primeiro, terceiro e quarto, obtemos imediatamente as primeiras integrais

${\ displaystyle {\ dot {t}} = {\ frac {E} {x ^ {2}}}, \; \; {\ dot {y}} = P, \; \; {\ dot {z} } = Q}$

Mas, a partir do elemento de linha, temos onde para geodésicas semelhantes a tempo, nula e espacial, respectivamente. Isso nos dá a quarta primeira integral, a saber ${\ displaystyle \ varepsilon = -x ^ {2} \, {\ dot {t}} ^ {2} + {\ dot {x}} ^ {2} + {\ dot {y}} ^ {2} + {\ ponto {z}} ^ {2}}$${\ displaystyle \ varepsilon \ in \ left \ {- 1, \, 0, \, 1 \ right \}}$

${\ displaystyle {\ dot {x}} ^ {2} = \ left (\ varepsilon + {\ frac {E ^ {2}} {x ^ {2}}} \ right) -P ^ {2} -Q ^ {2}}$.

Isso é suficiente para dar a solução completa das equações geodésicas.

No caso de geodésicas nulas , de com diferente de zero , vemos que a coordenada x varia ao longo do intervalo . ${\ displaystyle {\ frac {E ^ {2}} {x ^ {2}}} \, - \, P ^ {2} \, - \, Q ^ {2}}$${\ displaystyle E}$${\ displaystyle 0 \, <\, x \, <\, {\ frac {E} {\ sqrt {P ^ {2} \, + \, Q ^ {2}}}}}$

A família completa de sete parâmetros, fornecendo qualquer geodésica nula por meio de qualquer evento na cunha Rindler, é

${\ displaystyle {\ begin {alinhados} t-t_ {0} & = \ operatorname {artanh} \ left ({\ frac {1} {E}} \ left [s \ left (P ^ {2} + Q ^ {2} \ right) - {\ sqrt {E ^ {2} - \ left (P ^ {2} + Q ^ {2} \ right) x_ {0} ^ {2}}} \ right] \ right) + \\ & \ qquad \ operatorname {artanh} \ left ({\ frac {1} {E}} {\ sqrt {E ^ {2} - (P ^ {2} + Q ^ {2}) x_ {0 } ^ {2}}} \ right) \\ x & = {\ sqrt {x_ {0} ^ {2} + 2s {\ sqrt {E ^ {2} - (P ^ {2} + Q ^ {2} ) x_ {0} ^ {2}}} - s ^ {2} (P ^ {2} + Q ^ {2})}} \\ y-y_ {0} & = Ps; \; \; z- z_ {0} = Qs \ end {alinhado}}}$

Traçando os rastros de algumas geodésicas nulas representativas através de um determinado evento (isto é, projetando-se para o hiperslice ), obtemos uma imagem que se parece suspeitamente com a família de todos os semicírculos através de um ponto e ortogonal ao horizonte de Rindler (veja a figura). ${\ displaystyle t = 0}$

A métrica Fermat

O fato de que no gráfico de Rindler, as projeções de geodésicas nulas em qualquer hiperslice espacial para os observadores Rindler são simplesmente arcos semicirculares pode ser verificado diretamente a partir da solução geral que acabamos de dar, mas há uma maneira muito simples de ver isso. Um espaço - tempo estático é aquele em que um campo vetorial Killing livre de vorticidade pode ser encontrado. Neste caso, temos uma família definida de forma única de hiperslices espaciais (idênticas) ortogonais aos observadores estáticos correspondentes (que não precisam ser observadores inerciais). Isso nos permite definir uma nova métrica em qualquer um desses hiperslices que está conformalmente relacionada à métrica original herdada do espaço-tempo, mas com a propriedade de geodésica na nova métrica (observe que esta é uma métrica Riemanniana em uma variedade tripla Riemanniana) são precisamente as projeções das geodésicas nulas do espaço-tempo. Esta nova métrica é chamada de métrica Fermat , e em um espaço-tempo estático dotado de um gráfico de coordenadas em que o elemento de linha tem a forma

${\ displaystyle ds ^ {2} = g_ {00} \, dt ^ {2} + g_ {jk} \, dx ^ {j} \, dx ^ {k}, \; \; j, \; k \ em \ {1,2,3 \}}$

a métrica de Fermat é simplesmente ${\ displaystyle t = 0}$

${\ displaystyle d \ rho ^ {2} = {\ frac {1} {- g_ {00}}} \ left (g_ {jk} \, dx ^ {j} \, dx ^ {k} \ right)}$

(onde os coeficientes métricos são considerados para serem avaliados ). ${\ displaystyle t = 0}$

No gráfico de Rindler, a tradução semelhante ao tempo é um campo vetorial Killing, então este é um espaço-tempo estático (não surpreendentemente, uma vez que o espaço-tempo de Minkowski é trivialmente uma solução de vácuo estática da equação do campo de Einstein ). Portanto, podemos escrever imediatamente a métrica Fermat para os observadores Rindler: ${\ displaystyle \ partial _ {t}}$

${\ displaystyle d \ rho ^ {2} = {\ frac {1} {x ^ {2}}} \ left (dx ^ {2} + dy ^ {2} + dz ^ {2} \ right), \ ; \; \ forall x> 0, \; \; \ forall y, z}$

Mas este é o elemento de linha bem conhecido do H ³ hiperbólico de três espaços na metade superior do gráfico de espaço . Isso é intimamente análogo ao conhecido gráfico do meio plano superior para o plano hiperbólico H ² , que é familiar a gerações de estudantes de análise complexa em conexão com problemas de mapeamento conformado (e muito mais), e muitos leitores de mentalidade matemática já sabem que a geodésica de H ² no modelo do meio plano superior são simplesmente semicírculos (ortogonais ao círculo no infinito representado pelo eixo real).

Simetrias

Como o gráfico de Rindler é um gráfico de coordenadas para o espaço-tempo de Minkowski, esperamos encontrar dez campos de vetores Killing linearmente independentes. De fato, no gráfico cartesiano podemos encontrar prontamente dez campos de vetores Killing linearmente independentes, gerando respectivamente um subgrupo de parâmetro de tradução no tempo , três espaciais, três rotações e três impulsos. Juntos, eles geram o grupo Poincaré (isócrono adequado), o grupo de simetria do espaço-tempo de Minkowski.

No entanto, é instrutivo anotar e resolver as equações do vetor Killing diretamente. Obtemos quatro campos de vetores Killing de aparência familiar

${\ displaystyle \ partial _ {t}, \; \; \ partial _ {y}, \; \; \ partial _ {z}, \; \; - z \, \ partial _ {y} + y \, \ parcial _ {z}}$

(tradução de tempo, translações espaciais ortogonais à direção de aceleração e rotação espacial ortogonal à direção de aceleração) mais seis:

${\ displaystyle {\ begin {alinhado} & \ exp (\ pm t) \, \ left ({\ frac {y} {x}} \, \ partial _ {t} \ pm \ left [y \, \ partial _ {x} -x \, \ partial _ {y} \ right] \ right) \\ & \ exp (\ pm t) \, \ left ({\ frac {z} {x}} \, \ partial _ {t} \ pm \ left [z \, \ partial _ {x} -x \, \ partial _ {z} \ right] \ right) \\ & \ exp (\ pm t) \, \ left ({\ frac {1} {x}} \, \ parcial _ {t} \ pm \ parcial _ {x} \ direita) \ end {alinhado}}}$

(onde os sinais são escolhidos de forma consistente + ou -). Deixamos como exercício descobrir como eles se relacionam com os geradores padrão; aqui, desejamos apontar que devemos ser capazes de obter geradores equivalentes aos do gráfico cartesiano, embora a cunha de Rindler obviamente não seja invariante sob esta tradução. Como isso pode ser? A resposta é que, como qualquer coisa definida por um sistema de equações diferenciais parciais em uma variedade suave, a equação de Killing terá, em geral, soluções definidas localmente, mas podem não existir globalmente. Ou seja, com restrições adequadas no parâmetro de grupo, um fluxo de Killing sempre pode ser definido em uma vizinhança local adequada , mas o fluxo pode não ser bem definido globalmente . Isso não tem nada a ver com as variedades Lorentzianas per se, uma vez que a mesma questão surge no estudo das variedades suaves gerais . ${\ displaystyle \ partial _ {T}}$

Noções de distância

Uma das muitas lições valiosas a serem aprendidas com o estudo do mapa de Rindler é que existem de fato várias noções distintas (mas razoáveis) de distância que podem ser usadas pelos observadores de Rindler.

Significado operacional da distância de radar entre dois observadores Rindler (linhas verticais azuis marinho). O horizonte de Rindler é mostrado à esquerda (linha vertical vermelha). A linha mundial do pulso do radar também é representada, junto com os cones de luz (dimensionados corretamente) nos eventos A, B, C.

A primeira é aquela que empregamos tacitamente acima: a métrica Riemanniana induzida nos hiperslícios espaciais . Chamaremos isso de distância da régua, pois corresponde a essa métrica Riemanniana induzida, mas seu significado operacional pode não ser imediatamente aparente. ${\ displaystyle t = t_ {0}}$

Do ponto de vista da medição física, uma noção mais natural de distância entre duas linhas de mundo é a distância de radar . Isso é calculado enviando uma geodésica nula da linha de mundo de nosso observador (evento A) para a linha de mundo de algum objeto pequeno, após o que é refletido (evento B) e retorna ao observador (evento C). A distância do radar é então obtida dividindo o tempo de viagem de ida e volta, medido por um relógio ideal carregado por nosso observador.

(No espaço-tempo de Minkowski, felizmente, podemos ignorar a possibilidade de vários caminhos geodésicos nulos entre duas linhas de mundo, mas em modelos cosmológicos e outras aplicações as coisas não são tão simples. Devemos também advertir contra assumir que esta noção de distância entre dois observadores dá uma noção que é simétrica sob a troca de observadores.)

Em particular, considere um par de observadores Rindler com coordenadas e respectivamente. (Observe que o primeiro deles, o observador posterior, está acelerando um pouco mais forte, a fim de acompanhar o observador líder). Definindo no elemento de linha de Rindler, obtemos prontamente a equação de geodésicas nulas movendo-se na direção de aceleração: ${\ displaystyle x = x_ {0}, \; y = 0, \; z = 0}$${\ displaystyle x = x_ {0} + h, \; y = 0, \; z = 0}$${\ displaystyle dy = dz = 0}$

${\ displaystyle t-t_ {0} = \ log \ left ({\ frac {x} {x_ {0}}} \ right)}$

Portanto, a distância de radar entre esses dois observadores é dada por

${\ displaystyle x_ {0} \, \ log \ left (1 + {\ frac {h} {x_ {0}}} \ right) = h - {\ frac {h ^ {2}} {2 \, x_ {0}}} + O \ esquerda (h ^ {3} \ direita)}$

Isso é um pouco menor do que a distância da régua, mas para observadores próximos a discrepância é insignificante.

Uma terceira noção possível de distância é esta: nosso observador mede o ângulo subtendido por um disco unitário colocado em algum objeto (não um objeto pontual), conforme aparece de sua localização. Chamamos isso de distância do diâmetro óptico . Por causa do caráter simples de geodésicas nulas no espaço-tempo de Minkowski, podemos determinar prontamente a distância óptica entre nosso par de observadores Rindler (alinhados com a direção de aceleração). A partir de um esboço, deve ser plausível que a distância do diâmetro óptico seja dimensionada como . Portanto, no caso de um observador atrás estimando a distância para um observador líder (o caso ), a distância óptica é um pouco maior do que a distância da régua, que é um pouco maior do que a distância do radar. O leitor deve agora levar um momento para considerar o caso de um observador líder estimando a distância para um observador posterior. ${\ textstyle h + {\ frac {1} {x_ {0}}} + O \ left (h ^ {3} \ right)}$${\ displaystyle h> 0}$

Existem outras noções de distância, mas o ponto principal é claro: embora os valores dessas várias noções em geral discordem para um dado par de observadores Rindler, todos eles concordam que cada par de observadores Rindler mantém uma distância constante . O fato de que observadores Rindler muito próximos são mutuamente estacionários decorre do fato, observado acima, de que o tensor de expansão da congruência de Rindler desaparece de forma idêntica. No entanto, mostramos aqui que, em vários sentidos, essa propriedade de rigidez se mantém em escalas maiores. Esta é realmente uma propriedade de rigidez notável, dado o fato bem conhecido de que na física relativística nenhuma barra pode ser acelerada rigidamente (e nenhum disco pode ser girado rigidamente ) - pelo menos, não sem sustentar tensões não homogêneas. A maneira mais fácil de ver isso é observar que, na física newtoniana, se "chutarmos" um corpo rígido, todos os elementos da matéria no corpo mudarão imediatamente seu estado de movimento. É claro que isso é incompatível com o princípio relativístico de que nenhuma informação com efeito físico pode ser transmitida mais rápido do que a velocidade da luz.

Segue-se que se uma barra é acelerada por alguma força externa aplicada em qualquer lugar ao longo de seu comprimento, os elementos da matéria em vários lugares diferentes na barra não podem sentir a mesma magnitude de aceleração se a barra não se estender sem limites e finalmente quebrar. Em outras palavras, uma barra acelerada que não quebra deve suportar tensões que variam ao longo de seu comprimento. Além disso, em qualquer experimento mental com forças variáveis ​​no tempo, quer "chutemos" um objeto ou tentemos acelerá-lo gradualmente, não podemos evitar o problema de evitar modelos mecânicos que são inconsistentes com a cinemática relativística (porque partes distantes do corpo respondem muito rapidamente a uma força aplicada).

Voltando à questão do significado operacional da distância da régua, vemos que esta deve ser a distância que nossos observadores obterão se eles passarem muito lentamente de mão em mão uma pequena régua que é repetidamente ajustada de ponta a ponta. Mas justificar essa interpretação em detalhes exigiria algum tipo de modelo material.

Generalização para espaços-tempos curvos

As coordenadas de Rindler, conforme descrito acima, podem ser generalizadas para o espaço-tempo curvo, como coordenadas normais de Fermi . A generalização essencial envolve a construção de uma tétrade ortonormal apropriada e, em seguida, transportá-la ao longo da trajetória dada usando a regra de transporte de Fermi-Walker . Para obter detalhes, consulte o artigo de Ni e Zimmermann nas referências abaixo. Tal generalização realmente permite estudar os efeitos inerciais e gravitacionais em um laboratório baseado na Terra, bem como os efeitos acoplados inercial-gravitacionais mais interessantes.

História

Visão geral

Coordenadas de Kottler-Møller e Rindler

Albert Einstein (1907) estudou os efeitos dentro de um quadro uniformemente acelerado, obtendo equações para dilatação do tempo dependente de coordenadas e velocidade da luz equivalente a ( 2c ), e para fazer as fórmulas independentes da origem do observador, ele obteve dilatação do tempo ( 2i ) em acordo formal com as coordenadas do radar. Ao introduzir o conceito de rigidez de Born , Max Born (1909) observou que as fórmulas para movimento hiperbólico podem ser usadas como transformações em um "sistema de referência hiperbolicamente acelerado" ( alemão : hyperbolisch beschleunigtes Bezugsystem ) equivalente a ( 2d ). O trabalho de Born foi posteriormente elaborado por Arnold Sommerfeld (1910) e Max von Laue (1911) que ambos obtiveram ( 2d ) usando números imaginários , que foi resumido por Wolfgang Pauli (1921) que além das coordenadas ( 2d ) também obteve métrica ( 2e ) usando números imaginários. Einstein (1912) estudou um campo gravitacional estático e obteve a métrica Kottler-Møller ( 2b ), bem como aproximações para as fórmulas ( 2a ) usando uma velocidade da luz dependente das coordenadas. Hendrik Lorentz (1913) obteve coordenadas semelhantes a ( 2d , 2e , 2f ) ao estudar o princípio de equivalência de Einstein e o campo gravitacional uniforme.

Uma descrição detalhada foi dada por Friedrich Kottler (1914), que formulou a tétrade ortonormal , fórmulas de transformação e métricas correspondentes ( 2a , 2b ). Também Karl Bollert (1922) obteve a métrica ( 2b ) em seu estudo de aceleração uniforme e campos gravitacionais uniformes. Em um artigo sobre rigidez de Born, Georges Lemaître (1924) obteve coordenadas e métricas ( 2a , 2b ). Albert Einstein e Nathan Rosen (1935) descreveram ( 2d , 2e ) como as expressões "bem conhecidas" para um campo gravitacional homogêneo. Após Christian Møller (1943) obter ( 2a , 2b ) em um estudo relacionado a campos gravitacionais homogêneos, ele (1952) assim como Misner & Thorne & Wheeler (1973) usaram o transporte de Fermi-Walker para obter as mesmas equações.

Enquanto essas investigações estavam preocupadas com o espaço-tempo plano, Wolfgang Rindler (1960) analisou o movimento hiperbólico no espaço-tempo curvo e mostrou (1966) a analogia entre as coordenadas hiperbólicas ( 2d , 2e ) no espaço-tempo plano com as coordenadas de Kruskal no espaço de Schwarzschild . Isso influenciou escritores subsequentes em sua formulação da radiação Unruh medida por um observador em movimento hiperbólico, que é semelhante à descrição da radiação Hawking dos buracos negros .

Horizonte

Born (1909) mostrou que os pontos internos de um corpo rígido de Born em movimento hiperbólico só podem estar na região . Sommerfeld (1910) definiu que as coordenadas permitidas para a transformação entre coordenadas inerciais e hiperbólicas devem ser satisfeitas . Kottler (1914) definiu esta região como , e apontou a existência de um "plano de fronteira" ( alemão : Grenzebene ) , além do qual nenhum sinal pode chegar ao observador em movimento hiperbólico. Isso foi chamado de "horizonte do observador" ( alemão : Horizont des Beobachters ) por Bollert (1922). Rindler (1966) demonstrou a relação entre tal horizonte e o horizonte em coordenadas de Kruskal. ${\ displaystyle X / \ left (X ^ {2} -T ^ {2} \ right)> 0}$${\ displaystyle T <X}$${\ displaystyle X ^ {2} -T ^ {2}> 0}$${\ displaystyle c ^ {2} / \ alpha + x}$

Coordenadas de radar

Usando o formalismo de Bollert, Stjepan Mohorovičić (1922) fez uma escolha diferente para algum parâmetro e obteve a métrica ( 2h ) com um erro de impressão, que foi corrigido por Bollert (1922b) com outro erro de impressão, até que uma versão sem erro de impressão foi fornecida por Mohorovičić (1923). Além disso, Mohorovičić argumentou erroneamente que a métrica ( 2b , agora chamada de métrica Kottler-Møller) está incorreta, o que foi refutado por Bollert (1922). Metric ( 2h ) foi redescoberto por Harry Lass (1963), que também deu as coordenadas correspondentes ( 2g ) que às vezes são chamadas de "coordenadas Lass". Metric ( 2h ), assim como ( 2a , 2b ), também foi derivado por Fritz Rohrlich (1963). Eventualmente, as coordenadas de Lass ( 2g , 2h ) foram identificadas com as coordenadas do radar por Desloge & Philpott (1987).

Tabela com fórmulas históricas

Einstein (1907) ${\ displaystyle {\ scriptstyle {\ begin {matrix} \ sigma = \ tau \ left (1 + {\ frac {\ gamma \ xi} {c ^ {2}}} \ right) \\\ sigma = \ tau e ^ {\ gamma \ xi / c ^ {2}} \\ c \ left (1 + {\ frac {\ gamma \ xi} {c ^ {2}}} \ right) \ end {matriz}}}}$ Nasceu (1909) ${\ displaystyle {\ scriptstyle {\ begin {matrix} x = -q \ xi, \ y = \ eta, \ z = \ zeta, \ t = {\ frac {p} {c ^ {2}}} \ xi \\\ left (p = x _ {\ tau}, \ q = -t _ {\ tau} = {\ sqrt {1 + p ^ {2} / c ^ {2}}} \ right) \\ {\ boldsymbol {\ downarrow}} \\ x ^ {2} -c ^ {2} t ^ {2} = \ xi ^ {2} \ end {matriz}}}}$ Herglotz (1909) ${\ displaystyle {\ scriptstyle {\ begin {matrix} {\ begin {alinhados} x & = x '\\ y & = y' \\ tz & = (t'-z ') e ^ {\ vartheta} \\ t + z & = (t '+ z') e ^ {- \ vartheta} \ end {alinhado}} \\ {\ boldsymbol {\ downarrow}} \\ x = x_ {0}, \ quad y = y_ {0}, \ quad z = {\ sqrt {z_ {0} ^ {2} + t ^ {2}}} \ end {matriz}}}}$ Sommerfeld (1910) ${\ displaystyle \ scriptstyle {\ begin {alinhados} x & = r \ cos \ varphi \\ y & = y '\\ z & = z' \\ l & = r \ sin \ varphi \\\ varphi & = i \ psi, \ l = ict \ end {alinhado}}}$ von Laue (1911) ${\ displaystyle \ scriptstyle {\ begin {alinhados} X & = R \ cos \ varphi \\ L & = R \ sin \ varphi \\ R ^ {2} & = X ^ {2} + L ^ {2} \\\ tan \ varphi & = {\ frac {L} {X}} \ end {alinhado}}}$ Einstein (1912) ${\ displaystyle {\ scriptstyle {\ begin {matrix} d \ xi ^ {2} -d \ tau ^ {2} = dx ^ {2} -c ^ {2} dt ^ {2} \\ {\ boldsymbol { \ downarrow}} \\ c = c_ {0} + ax \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {alinhados} \ xi & = x + {\ frac {ac} {2}} t ^ { 2} \\\ eta & = y \\\ zeta & = z \\\ tau & = ct \ end {alinhado}} \ end {matriz}}}}$ Kottler (1912) ${\ displaystyle {\ scriptstyle {\ begin {alinhados} x ^ {(1)} & = x_ {0} ^ {(1)} \\ x ^ {(2)} & = x_ {0} ^ {(2) )} \\ x ^ {(3)} & = b \ cos i \ varphi \\ x ^ {(4)} & = b \ sin i \ varphi \ end {alinhado}}}}$ Lorentz (1913) ${\ displaystyle {\ scriptstyle {\ begin {matrix} dc = {\ frac {g} {c}} dz \\\ hline {\ begin {alinhados} z & = a \ left (z'-z_ {0} ^ { \ prime} \ right) \\ ct & = b \ left (z'-z_ {0} ^ {\ prime} \ right) \\ a & = {\ frac {1} {2}} \ left (e ^ {kt '} + e ^ {- kt} \ right) \\ b & = {\ frac {1} {2}} \ left (e ^ {kt'} - e ^ {- kt} \ right) \ end {alinhado} } \\ {\ boldsymbol {\ downarrow}} \\ c '= k \ left (z'-z_ {0} ^ {\ prime} \ right), \ z'-z_ {0} ^ {\ prime} = {\ frac {c ^ {2}} {g}} \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {align} & dx ^ {2} + dy ^ {2} + dz ^ {2} - c ^ {2} dt \\ & = dx ^ {\ prime 2} + dy ^ {\ prime 2} + dz ^ {\ prime 2} -c ^ {\ prime 2} dt ^ {\ prime 2} \ end {alinhado}} \ end {matriz}}}}$

Kottler (1914a) ${\ displaystyle {\ scriptstyle {\ begin {matrix} {\ begin {alinhados} x ^ {(1)} & = x_ {0} ^ {(1)} \\ x ^ {(2)} & = x_ { 0} ^ {(2)} \\ x ^ {(3)} & = b \ cos iu \\ x ^ {(4)} & = b \ sin iu \ end {alinhado}} \\ {\ boldsymbol { \ downarrow}} \\ ds ^ {2} = - c ^ {2} d \ tau ^ {2} = b ^ {2} (du) ^ {2} \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {matrix} c_ {1} ^ {(1)} = 0, && c_ {1} ^ {(2)} = 0, && c_ {1} ^ {(3)} = - \ sin iu, && c_ { 1} ^ {(4)} = \ cos iu, \\ c_ {2} ^ {(1)} = 0, && c_ {2} ^ {(2)} = 0, && c_ {2} ^ {(3) } = - \ cos iu, && c_ {2} ^ {(4)} = - \ sin iu, \ end {matriz}} \\ {\ boldsymbol {\ downarrow}} \\ dS ^ {2} = (dX ' ) ^ {2} + (dY ') ^ {2} + (dZ') ^ {2} - \ left (c + {\ frac {Z'c} {b}} \ right) ^ {2} dT '\ \ {\ boldsymbol {\ downarrow}} \\ c '= c + {\ frac {Z'c ^ {2}} {b}} \ cdot {\ frac {1} {c}} \ end {matriz}}} }$ Kottler (1914b) ${\ displaystyle \ scriptstyle {\ begin {matrix} {\ begin {matrix} c_ {1} ^ {(1)} = 0, && c_ {1} ^ {(2)} = 0, && c_ {1} ^ {( 3)} = {\ frac {1} {i}} \ sinh u, && c_ {1} ^ {(4)} = \ cosh u, \\ c_ {2} ^ {(1)} = 0, && c_ { 2} ^ {(2)} = 0, && c_ {2} ^ {(3)} = {\ frac {1} {i}} \ cosh u, && c_ {2} ^ {(4)} = - \ sinh u, \\ c_ {3} ^ {(1)} = 1, && c_ {3} ^ {(2)} = 0, && c_ {3} ^ {(3)} = 0, && c_ {3} ^ {( 4)} = 0, \\ c_ {4} ^ {(1)} = 0, && c_ {4} ^ {(2)} = 1, && c_ {4} ^ {(3)} = 0, && c_ {4 } ^ {(4)} = 0, \ end {matriz}} \\ {\ boldsymbol {\ downarrow}} \\ X = x + \ Delta ^ {(2)} c_ {2} + \ Delta ^ {(3 )} c_ {3} + \ Delta ^ {(4)} c_ {4} \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {alinhados} X & = x_ {0} + {\ mathfrak {X} } '\\ Y & = y_ {0} + {\ mathfrak {Y}}' \\ Z & = \ left (b + {\ mathfrak {Z}} '\ right) \ cosh {\ mathfrak {u}} \\ cT & = \ left (b + {\ mathfrak {Z}} '\ right) \ sinh {\ mathfrak {u}} \ end {alinhado}} \\\ left (\ Delta ^ {(2)} = {\ mathfrak {X }} ', \ \ Delta ^ {(3)} = {\ mathfrak {Y}}', \ \ Delta ^ {(4)} = {\ mathfrak {Z}} '\ right) \\ {\ boldsymbol { \ downarrow}} \\ {\ begin {align} {\ mathfrak {X}} '& = X_ {0} -x_ {0} + q_ {x} T \\ {\ mathfrak {Y}}' & = Y_ {0} -y_ {0} + q_ {y} T \\ b + {\ mathfrak {Z}} '& = {\ sqrt {\ left (Z_ {0} + q_ {x} T \ right) ^ {2 } -c ^ {2} T ^ {2}} } \\ c {\ mathfrak {T}} '& = b \ operatorname {artanh} {\ frac {cT} {Z_ {0} + q_ {x} T}} \ end {alinhado}} \\\ left ( X = X_ {0} + q_ {x} T, \ Y = Y_ {0} + q_ {y} T, \ Z = Z_ {0} + q_ {x} T \ right) \\ {\ boldsymbol {\ downarrow}} \\ dS ^ {2} = (d {\ mathfrak {X}} ') ^ {2} + (d {\ mathfrak {Y}}') ^ {2} + (d {\ mathfrak {Z }} ') ^ {2} -c ^ {2} \ left ({\ frac {b + {\ mathfrak {Z}}'} {b ^ {2}}} \ right) ^ {2} (d {\ mathfrak {T}} ') ^ {2} \ end {matriz}}}$ Kottler (1916,1918) ${\ displaystyle \ scriptstyle {\ begin {matrix} {\ begin {alinhados} x & = x '\\ y & = y' \\ {\ frac {c ^ {2}} {\ gamma}} + z & = \ left ( {\ frac {c ^ {2}} {\ gamma}} + z '\ right) \ cosh {\ frac {\ gamma t'} {c}} \\ ct & = \ left ({\ frac {c ^ { 2}} {\ gamma}} + z '\ right) \ sinh {\ frac {\ gamma t'} {c}} \ end {alinhados}} \\ {\ boldsymbol {\ downarrow}} \\ ds ^ { 2} = dx ^ {\ prime 2} + dy ^ {\ prime 2} + dz ^ {\ prime 2} - \ left (c + {\ frac {\ gamma} {c}} z '\ right) {} ^ {2} dt ^ {\ prime 2} \ end {matriz}}}$

Pauli (1921) ${\ displaystyle \ scriptstyle {\ begin {matrix} {\ begin {alinhados} x ^ {1} & = \ varrho \ cos \ varphi \\ x ^ {4} & = \ varrho \ sin \ varphi \ end {alinhados} } \\ {\ boldsymbol {\ downarrow}} \\ ds ^ {2} = \ left (d \ xi ^ {1} \ right) ^ {2} + \ left (d \ xi ^ {2} \ right) ^ {2} + \ left (d \ xi ^ {3} \ right) ^ {2} + \ left (\ xi ^ {1} \ right) ^ {2} \ left (d \ xi ^ {4} \ direita) ^ {2} \\\ esquerda (\ xi ^ {(1)} = \ varrho, \ \ xi ^ {(2)} = x ^ {(2)}, \ \ xi ^ {(3)} = x ^ {(3)}, \ \ xi ^ {(4)} = \ varphi \ right) \ end {matriz}}}$ Bollert (1922) ${\ displaystyle {\ scriptstyle {\ begin {matrix} ds ^ {2} = c ^ {2} \ left (1 + {\ frac {\ gamma _ {0} x} {c ^ {2}}} \ right ) d \ tau ^ {2} -dx ^ {2} -dy ^ {2} -dz ^ {2} \\\ hline ds ^ {2} = g_ {44} dx_ {4} ^ {2} + g_ {11} dx_ {1} ^ {2} + g_ {22} \ left (dx_ {2} ^ {2} + dx_ {3} ^ {2} \ right) \\ {\ boldsymbol {\ downarrow}} \ \ V '' - {\ frac {g_ {11}} {2g_ {11}}} V '= 0 \\\ esquerda (g_ {22} = - 1, \ g_ {11} = - 1, \ V' '= 0, \ V = ax + b \ right) \\ {\ boldsymbol {\ downarrow}} \\ ds ^ {2} = dx_ {4} ^ {2} (ax + b) ^ {2} -dx ^ {2} -dy ^ {2} -dz ^ {2} \ end {matrix}}}}$ Mohorovičić (1922,1923); Bollert (1922b) ${\ displaystyle {\ scriptstyle {\ begin {matrix} {\ text {Mohorovičić (1922):}} \\ g_ {11} = g_ {44} = V ^ {2}, \ VV '' - V '^ { 2} = 0, \ V \ left (x_ {1} \ right) = e ^ {ax_ {1}} \\ {\ boldsymbol {\ downarrow}} \\ ds ^ {2} = e ^ {2a} \ esquerda (-dx_ {4} ^ {2} + dx_ {1} ^ {2} \ direita) + dx_ {2} ^ {2} + dx_ {3} ^ {2} \\\\ {\ text {corrigido por Bollert (1922b):}} \\ ds ^ {2} = e ^ {2ax} \ left (-dx_ {4} ^ {2} + dx_ {1} ^ {2} \ right) + dx_ {2} ^ {2} + dx_ {3} ^ {2} \\\\ {\ text {correção final por Mohorovičić (1923):}} \\ ds ^ {2} = e ^ {2ax_ {1}} \ left ( -dx_ {4} ^ {2} + dx_ {1} ^ {2} \ right) + dx_ {2} ^ {2} + dx_ {3} ^ {2} \ end {matrix}}}}$ Lemaître (1924) ${\ displaystyle {\ scriptstyle {\ begin {matrix} {\ begin {alinhado} 1 + g \ xi = & (1 + gx) \ cosh gt \\ g \ tau = & (1 + gx) \ sinh gt \ end {alinhado}} \\ {\ boldsymbol {\ downarrow}} \\ ds ^ {2} = - dx ^ {2} -dy ^ {2} -dz ^ {2} + (1 + gx) ^ {2} dt ^ {2} \ end {matriz}}}}$ Einstein & Rosen (1935) ${\ displaystyle \ scriptstyle {\ begin {matrix} {\ begin {alinhado} \ xi _ {1} & = x_ {1} \ cosh \ alpha x_ {4} \\\ xi _ {2} & = x_ {2 } \\\ xi _ {3} & = x_ {3} \\\ xi _ {4} & = x_ {1} \ sinh \ alpha x_ {4} \ end {alinhado}} \\ {\ boldsymbol {\ downarrow}} \\ ds ^ {2} = - dx_ {1} ^ {2} -dx_ {2} ^ {2} -dx_ {3} ^ {2} + \ alpha {} ^ {2} x_ {1 } ^ {2} dx_ {4} ^ {2} \ end {matriz}}}$ Møller (1952) ${\ displaystyle \ scriptstyle {\ begin {matrix} \ alpha _ {ik} = \ left ({\ begin {matrix} U_ {4} / ic & 0 & 0 & iU_ {1} / c \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ U_ {1} / ic & 0 & 0 & U_ {4} / ic \ end {matrix}} \ right) \\ U_ {i} = \ left (c \ sinh {\ frac {g \ tau} {c}}, \ 0,0, \ ig \ cosh {\ frac {g \ tau} {c}} \ right) \\ {\ boldsymbol {\ downarrow}} \\ X_ {i} = \ mathbf {f} _ {i} (t) + x ^ {\ prime \ kappa} \ alpha _ {\ kappa i} (\ tau) \\ {\ boldsymbol {\ downarrow}} \\ {\ begin {alinhados} X & = {\ frac {c ^ {2}} {g}} \ left (\ cosh {\ frac {gt} {c}} - 1 \ right) + x \ cosh {\ frac {gt} {c}} \\ Y & = y \\ Z & = z \\ T & = {\ frac {c} {g}} \ sinh {\ frac {gt} {c}} + x {\ frac {\ sinh {\ frac {gt} {c}}} {c}} \ end {alinhado}} \ \ {\ boldsymbol {\ downarrow}} \\ ds ^ {2} = dx ^ {2} + dy ^ {2} + dz ^ {2} -c ^ {2} dt ^ {2} \ left (1+ gx / c ^ {2} \ right) ^ {2} \\\\\ end {matrix}}}$

Veja também

• Paradoxo da nave espacial de Bell , para um assunto às vezes controverso, muitas vezes estudado usando coordenadas de Rindler.
• Coordenadas nascidas , para outro importante sistema de coordenadas adaptado ao movimento de certos observadores acelerados no espaço-tempo de Minkowski .
• Congruência (relatividade geral)
• Paradoxo de Ehrenfest , para um assunto às vezes controverso, muitas vezes estudado usando as coordenadas de Born.
• Campos de quadro na relatividade geral
• Recursos da relatividade geral
• Modelo milne
• Equação de Raychaudhuri
• Efeito Unruh

Referências