Regressão segmentada - Segmented regression
| Parte de uma série sobre |
| Análise de regressão |
|---|
| Modelos |
| Estimativa |
| Fundo |
A regressão segmentada , também conhecida como regressão por partes ou regressão quebrada , é um método de análise de regressão em que a variável independente é particionada em intervalos e um segmento de linha separado é ajustado para cada intervalo. A análise de regressão segmentada também pode ser realizada em dados multivariados, particionando as várias variáveis independentes. A regressão segmentada é útil quando as variáveis independentes, agrupadas em grupos diferentes, exibem relacionamentos diferentes entre as variáveis nessas regiões. Os limites entre os segmentos são pontos de interrupção .
A regressão linear segmentada é uma regressão segmentada em que as relações nos intervalos são obtidas por regressão linear .
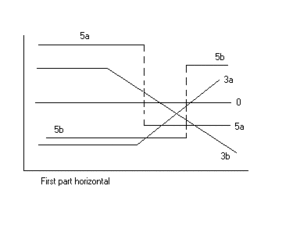
Regressão linear segmentada, dois segmentos
A regressão linear segmentada com dois segmentos separados por um ponto de interrupção pode ser útil para quantificar uma mudança abrupta da função de resposta (Yr) de um fator influente variável ( x ). O ponto de interrupção pode ser interpretado como um valor crítico , seguro ou limite além ou abaixo do qual ocorrem efeitos (des) desejados. O ponto de interrupção pode ser importante na tomada de decisão
As figuras ilustram alguns dos resultados e tipos de regressão que podem ser obtidos.
Uma análise de regressão segmentada baseia-se na presença de um conjunto de ( y, x dados), em que y é a variável dependente e x a variável independente .
O método dos mínimos quadrados aplicado separadamente a cada segmento, pelo qual as duas linhas de regressão são feitas para ajustar o conjunto de dados o mais próximo possível, minimizando a soma dos quadrados das diferenças (SSD) entre os valores observados ( y ) e calculados (Yr) da variável dependente, resulta nas duas equações a seguir:
- Ano = A 1 . x + K 1 para x <BP (ponto de interrupção)
- Yr = A 2 . x + K 2 para x > BP (ponto de interrupção)
Onde:
- Yr é o valor esperado (previsto) de y para um certo valor de x ;
- A 1 e A 2 são coeficientes de regressão (indicando a inclinação dos segmentos de linha);
- K 1 e K 2 são constantes de regressão (indicando a interceptação no eixo y ).
Os dados podem mostrar muitos tipos ou tendências, veja as figuras.
O método também produz dois coeficientes de correlação (R):
- para x <BP (ponto de interrupção)
e
- para x > BP (ponto de interrupção)
Onde:
- é o SSD minimizado por segmento
e
- Y a1 e Y a2 são os valores médios de y nos respectivos segmentos.
Na determinação da tendência mais adequada, testes estatísticos devem ser realizados para garantir que essa tendência seja confiável (significativa).
Quando nenhum ponto de interrupção significativo pode ser detectado, deve-se recorrer a uma regressão sem ponto de interrupção.
Exemplo
Para a figura azul à direita que dá a relação entre o rendimento de mostarda (Yr = Ym, t / ha) e a salinidade do solo ( x = Ss, expressa como condutividade elétrica da solução do solo EC em dS / m), verifica-se que :
BP = 4,93, A 1 = 0, K 1 = 1,74, A 2 = −0,129, K 2 = 2,38, R 1 2 = 0,0035 (insignificante), R 2 2 = 0,395 (significativo) e:
- Ym = 1,74 t / ha para Ss <4,93 (ponto de interrupção)
- Ym = −0,129 Ss + 2,38 t / ha para Ss> 4,93 (ponto de interrupção)
indicando que as salinidades do solo <4,93 dS / m são seguras e as salinidades do solo> 4,93 dS / m reduzem o rendimento @ 0,129 t / ha por unidade de aumento da salinidade do solo.
A figura também mostra intervalos de confiança e incerteza conforme elaborado a seguir.
Procedimentos de teste
Os seguintes testes estatísticos são usados para determinar o tipo de tendência:
- significância do ponto de interrupção (BP), expressando BP como uma função dos coeficientes de regressão A 1 e A 2 e as médias Y 1 e Y 2 dos dados y e as médias X 1 e X 2 dos dados x (esquerdo e direito de BP), usando as leis de propagação de erros em adições e multiplicações para calcular o erro padrão (SE) de BP, e aplicando o teste t de Student
- significância de A 1 e A 2 aplicando a distribuição t de Student e o erro padrão SE de A 1 e A 2
- significância da diferença de A 1 e A 2 aplicando a distribuição t de Student usando o SE de sua diferença.
- significância da diferença de Y 1 e Y 2 aplicando a distribuição t de Student usando o SE de sua diferença.
- Uma abordagem estatística mais formal para testar a existência de um ponto de interrupção é por meio do teste de pseudo pontuação, que não requer estimativa da linha segmentada.
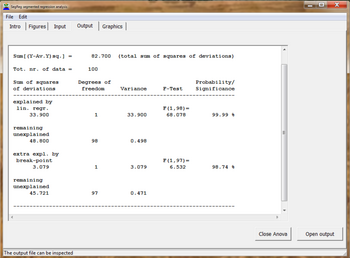
Além disso, é feito uso do coeficiente de correlação de todos os dados (Ra), o coeficiente de determinação ou coeficiente de explicação, os intervalos de confiança das funções de regressão e a análise ANOVA .
O coeficiente de determinação para todos os dados (Cd), que deve ser maximizado nas condições estabelecidas pelos testes de significância, é encontrado a partir de:
onde Yr é o valor esperado (previsto) de y de acordo com as equações de regressão anteriores e Ya é a média de todos os valores de y .
O coeficiente Cd varia entre 0 (nenhuma explicação) a 1 (explicação completa, correspondência perfeita).
Em uma regressão linear pura, não segmentada, os valores de Cd e Ra 2 são iguais. Em uma regressão segmentada, o Cd precisa ser significativamente maior do que Ra 2 para justificar a segmentação.
O valor ideal do ponto de interrupção pode ser encontrado de forma que o coeficiente Cd seja máximo .
Faixa sem efeito
A regressão segmentada é freqüentemente usada para detectar em qual intervalo uma variável explicativa (X) não tem efeito sobre a variável dependente (Y), enquanto além do alcance há uma resposta clara, seja ela positiva ou negativa. O alcance de nenhum efeito pode ser encontrado na parte inicial do domínio X ou, inversamente, em sua última parte. Para a análise "sem efeito", a aplicação do método dos mínimos quadrados para a análise de regressão segmentada pode não ser a técnica mais apropriada porque o objetivo é encontrar o trecho mais longo sobre o qual a relação YX pode ser considerada como tendo inclinação zero enquanto além o alcance da inclinação é significativamente diferente de zero, mas o conhecimento sobre o melhor valor dessa inclinação não é material. O método para encontrar o intervalo sem efeito é a regressão parcial progressiva ao longo do intervalo, estendendo o intervalo com pequenos passos até que o coeficiente de regressão seja significativamente diferente de zero.
Na próxima figura, o ponto de quebra é encontrado em X = 7,9, enquanto para os mesmos dados (veja a figura azul acima para produção de mostarda), o método dos mínimos quadrados produz um ponto de quebra apenas em X = 4,9. O último valor é menor, mas o ajuste dos dados além do ponto de interrupção é melhor. Portanto, dependerá do propósito da análise qual método precisa ser empregado.
Veja também
- Teste de comida
- Regressão simples
- Regressão linear
- Mínimos quadrados comuns
- Splines de regressão adaptativa multivariada
- Regressão local
- Projeto de descontinuidade de regressão
- Regressão Stepwise
- SegReg (software) para regressão segmentada
Referências
- ^ Análise de frequência e regressão . Capítulo 6 em: HPRitzema (ed., 1994), Drainage Principles and Applications , Publ. 16, pp. 175-224, Instituto Internacional para Recuperação e Melhoramento de Terras (ILRI), Wageningen, Holanda. ISBN 90-70754-33-9 . Download grátis da página web [1] , sob o nr. 20, ou diretamente como PDF: [2]
- ^ Pesquisa de drenagem em campos dos fazendeiros: análise de dados . Parte do projeto "Ouro líquido" do Instituto Internacional para Recuperação e Melhoramento de Terras (ILRI), Wageningen, Holanda. Baixe como PDF: [3]
- ^ RJOosterbaan, DPSharma, KNSingh e KVGKRao, 1990, Produção de safra e salinidade do solo: avaliação de dados de campo da Índia por regressão linear segmentada . In: Anais do Simpósio sobre Drenagem de Terras para Controle de Salinidade em Regiões Áridas e Semi-áridas, 25 de fevereiro a 2 de março de 1990, Cairo, Egito, Vol. 3, Sessão V, p. 373-383.
- ^ Muggeo, VMR (2016). "Teste com um parâmetro incômodo presente apenas na alternativa: uma abordagem baseada em pontuação com aplicação à modelagem segmentada" (PDF) . Journal of Statistical Computation and Simulation . 86 (15): 3059–3067. doi : 10.1080 / 00949655.2016.1149855 .
- ^ A significância estatística de regressão linear segmentada com point break-usando análise de variância e F-testes . Baixe de [4] sob o nr. 13, ou diretamente como PDF: [5]
- ^ Análise de regressão segmentada, instituto internacional para a recuperação e a melhoria de terras (ILRI), Wageningen, os Países Baixos. Download grátis da página da web [6]
- ^ Análise parcial da regressão, instituto internacional para a recuperação e a melhoria da terra (ILRI), Wageningen, os Países Baixos. Download grátis da página da web [7]