Fórmula do cadarço - Shoelace formula

A fórmula do cadarço ou algoritmo do cadarço (também conhecido como fórmula da área de Gauss e fórmula do agrimensor ) é um algoritmo matemático para determinar a área de um polígono simples cujos vértices são descritos por suas coordenadas cartesianas no plano. O usuário multiplica as coordenadas correspondentes para encontrar a área que abrange o polígono e a subtrai do polígono circundante para encontrar a área do polígono dentro. É chamada de fórmula do cadarço por causa da multiplicação cruzada constante das coordenadas que compõem o polígono, como enfiar os cadarços. Às vezes também é chamado de método do cadarço . Tem aplicações em agrimensura e silvicultura, entre outras áreas.

A fórmula foi descrita por Albrecht Ludwig Friedrich Meister (1724–1788) em 1769 e por Carl Friedrich Gauss em 1795. Ela pode ser verificada dividindo o polígono em triângulos e pode ser considerada um caso especial do teorema de Green .

A fórmula da área é derivada tomando cada aresta AB e calculando a área do triângulo ABO com um vértice na origem O , pegando o produto vetorial (que dá a área de um paralelogramo ) e dividindo por 2. Quando um se enrola o polígono, esses triângulos com área positiva e negativa se sobreporão, e as áreas entre a origem e o polígono serão canceladas e somadas a 0, enquanto apenas a área dentro do triângulo de referência permanece. É por isso que a fórmula é chamada de fórmula do agrimensor, uma vez que o "agrimensor" está na origem; se for no sentido anti-horário, a área positiva é adicionada ao ir da esquerda para a direita e a área negativa é adicionada ao ir da direita para a esquerda, da perspectiva da origem.

A fórmula da área também pode ser aplicada a polígonos de sobreposição automática, uma vez que o significado da área ainda é claro, embora os polígonos de sobreposição não sejam geralmente simples . Além disso, um polígono auto-sobreposto pode ter múltiplas "interpretações", mas a fórmula do cadarço pode ser usada para mostrar que a área do polígono é a mesma, independentemente da interpretação.

Demonstração

A fórmula pode ser representada pela expressão

${\ displaystyle {\ begin {alinhados} \ mathbf {A} & = {1 \ over 2} \ left | \ left (\ sum _ {i = 1} ^ {n-1} x_ {i} y_ {i + 1} \ right) + x_ {n} y_ {1} - \ left (\ sum _ {i = 1} ^ {n-1} x_ {i + 1} y_ {i} \ right) -x_ {1} y_ {n} \ right | \\ [4pt] & = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + \ cdots + x_ {n-1} y_ { n} + x_ {n} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} - \ cdots -x_ {n} y_ {n-1} -x_ {1} y_ { n} | \ end {alinhado}}}$

Onde

• A é a área do polígono,
• n é o número de lados do polígono, e
• ( x _i ,  y _i ), i  = 1, 2, ...,  n são os vértices ordenados (ou "vértices") do polígono.

alternativamente

${\ displaystyle {\ begin {alinhados} \ mathbf {A} & = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} x_ {i} (y_ {i + 1} -y_ {i-1}) \ right | = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} y_ {i} (x_ {i + 1} -x_ {i-1}) \ right | = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} (x_ {i} y_ {i + 1} -x_ {i + 1} y_ {i}) \ right | \\ [5pt] & = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} (x_ {i + 1} + x_ {i}) (y_ {i + 1} - y_ {i}) \ right | = {1 \ over 2} \ left | \ sum _ {i = 1} ^ {n} \ det {\ begin {pmatrix} x_ {i} & x_ {i + 1} \\ y_ {i} & y_ {i + 1} \ end {pmatriz}} \ direita | \ end {alinhado}}}$

onde x _{n 1} = x ₁ e x ₀ = x _n , bem como y _{n + 1} = Y ₁ e Y ₀ = y _n .

Se os pontos forem rotulados sequencialmente no sentido anti-horário, então a soma dos determinantes acima é positiva e os sinais de valor absoluto podem ser omitidos; se eles forem rotulados no sentido horário, a soma dos determinantes será negativa. Isso ocorre porque a fórmula pode ser vista como um caso especial do teorema de Green .

Uma declaração particularmente concisa da fórmula pode ser dada em termos de álgebra exterior . Se forem os vértices consecutivos do polígono (considerados como vetores no plano cartesiano), então ${\ displaystyle v_ {1}, \ dots, v_ {n}}$

${\ displaystyle A = {\ frac {1} {2}} \ cdot \ left | \ sum _ {i = 1} ^ {n} v_ {i} \ wedge v_ {i + 1} \ right |.}$

Provas

Prova de triângulo

Referindo-se à figura, seja a área do triângulo cujos vértices são dados pelas coordenadas e desenhe o retângulo de área mínima ao redor do triângulo de forma que seus lados sejam paralelos aos eixos ou . Pelo menos um vértice do triângulo estará em um canto do retângulo. Na figura, as áreas dos três triângulos circundantes são e Obviamente é igual à área do retângulo (chame-o ) menos as áreas dos outros três triângulos: ${\ displaystyle \ mathbf {A}}$${\ displaystyle (x_ {1}, y_ {1}), (x_ {2}, y_ {2}),}$${\ displaystyle (x_ {3}, y_ {3}).}$${\ displaystyle x}$${\ displaystyle y}$${\ displaystyle \ mathbf {C}, \ mathbf {D},}$${\ displaystyle \ mathbf {E}.}$${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {R}}$

${\ displaystyle \ mathbf {A} = \ mathbf {R} - \ mathbf {C} - \ mathbf {D} - \ mathbf {E}}$

Pela inspeção da figura, pode-se perceber que as áreas são dadas por

${\ displaystyle \ mathbf {R} = (x_ {3} -x_ {2}) (y_ {1} -y_ {3}) = (x_ {3} y_ {1} + x_ {2} y_ {3} ) - (x_ {3} y_ {3} + x_ {2} y_ {1})}$

${\ displaystyle - \ mathbf {C} = - {\ frac {1} {2}} (x_ {3} -x_ {2}) (y_ {2} -y_ {3}) = {\ frac {1} {2}} (- x_ {3} y_ {2} -x_ {2} y_ {3}) + {\ frac {1} {2}} (x_ {3} y_ {3} + x_ {2} y_ {2})}$

${\ displaystyle - \ mathbf {D} = - {\ frac {1} {2}} (x_ {3} -x_ {1}) (y_ {1} -y_ {3}) = {\ frac {1} {2}} (- x_ {3} y_ {1} -x_ {1} y_ {3}) + {\ frac {1} {2}} (x_ {3} y_ {3} + x_ {1} y_ {1})}$

${\ displaystyle - \ mathbf {E} = - {\ frac {1} {2}} (x_ {1} -x_ {2}) (y_ {1} -y_ {2}) = {\ frac {1} {2}} (- x_ {1} y_ {1} -x_ {2} y_ {2}) + {\ frac {1} {2}} (x_ {1} y_ {2} + x_ {2} y_ {1})}$

Coletar termos e reorganizar rendimentos

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} ((x_ {2} y_ {3} -x_ {3} y_ {2}) - (x_ {1} y_ {3} - x_ {3} y_ {1}) + (x_ {1} y_ {2} -x_ {2} y_ {1}))}$

que pode ser escrito como um determinante

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} {\ begin {vmatrix} 1 & 1 & 1 \\ x_ {1} & x_ {2} & x_ {3} \\ y_ {1} & y_ {2} & y_ {3} \ end {vmatrix}}}$

Se as coordenadas forem escritas no sentido horário, o valor do determinante será ${\ displaystyle - \ mathbf {A}.}$

Reorganizando de outra forma

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1} -x_ {2 } y_ {1} -x_ {3} y_ {2} -x_ {1} y_ {3} |}$

que é a forma da fórmula do cadarço. Esta fórmula pode ser estendida para encontrar a área de qualquer polígono, pois um polígono simples pode ser dividido em triângulos.

Prova de quadrilátero e polígono geral

Encontrar a área de um quadrilátero demonstra como a fórmula do cadarço é generalizada para qualquer polígono dividindo o polígono em triângulos. Considere a figura de um quadrilátero cujas coordenadas são rotuladas no sentido anti-horário. O quadrilátero é dividido em dois triângulos com áreas e usando a fórmula do triângulo em cada triângulo obtemos ${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {B}.}$

${\ displaystyle \ mathbf {A} = {\ frac {1} {2}} (x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1} -x_ {2 } y_ {1} -x_ {3} y_ {2} -x_ {1} y_ {3})}$

${\ displaystyle \ mathbf {B} = {\ frac {1} {2}} (x_ {1} y_ {3} + x_ {3} y_ {4} + x_ {4} y_ {1} -x_ {3 } y_ {1} -x_ {4} y_ {3} -x_ {1} y_ {4})}$

Como os dois triângulos foram traçados no sentido anti-horário, ambas as áreas são positivas e obtemos a área do quadrilátero adicionando as duas áreas. O último termo positivo e o último termo negativo de cancelar com o primeiro termo positivo e o primeiro termo negativo de doação ${\ displaystyle \ mathbf {A}}$${\ displaystyle \ mathbf {B}}$

${\ displaystyle \ mathbf {A} _ {\ text {quad.}} = {\ frac {1} {2}} (x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3 } y_ {4} + x_ {4} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {4} y_ {3} -x_ {1} y_ {4} ).}$

Exemplos

O usuário deve conhecer os pontos do polígono em um plano cartesiano. Por exemplo, pegue um triângulo com coordenadas {(2, 1), (4, 5), (7, 8)}. Pegue a primeira coordenada x e multiplique-a pelo segundo valor y , então pegue a segunda coordenada x e multiplique-a pelo terceiro valor y , e repita quantas vezes até que seja feito para todos os pontos desejados. Isso pode ser representado pela seguinte fórmula:

${\ displaystyle \ mathbf {A} _ {\ text {tri.}} = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {1 } -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {1} y_ {3} |}$

para x _i e y _i representando cada respectiva coordenada. Esta fórmula é apenas a expansão daquelas dadas acima para o caso n = 3. Usando-a, pode-se descobrir que a área do triângulo é igual a metade do valor absoluto de 10 + 32 + 7 - 4 - 35 - 16, que é igual a 3. O número de variáveis ​​depende do número de lados do polígono . Por exemplo, um pentágono será definido acima para X ₅ e Y ₅ :

${\ displaystyle \ mathbf {A} _ {\ text {pent.}} = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {4 } + x_ {4} y_ {5} + x_ {5} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {4} y_ {3} -x_ {5 } y_ {4} -x_ {1} y_ {5} |}$

e um quadrilátero será definido acima para X ₄ e Y ₄ :

${\ displaystyle \ mathbf {A} _ {\ text {quad.}} = {1 \ over 2} | x_ {1} y_ {2} + x_ {2} y_ {3} + x_ {3} y_ {4 } + x_ {4} y_ {1} -x_ {2} y_ {1} -x_ {3} y_ {2} -x_ {4} y_ {3} -x_ {1} y_ {4} |.}$

Exemplo mais complexo

Considere o polígono definido pelos pontos (3, 4), (5, 11), (12, 8), (9, 5) e (5, 6), conforme ilustrado no diagrama.

A área deste polígono é:

${\ displaystyle {\ begin {alinhados} \ mathbf {A} & = {1 \ over 2} \, {\ big |} 3 \ vezes 11 + 5 \ vezes 8 + 12 \ vezes 5 + 9 \ vezes 6 + 5 \ times 4 \\ & {} \ qquad {} -4 \ times 5-11 \ times 12-8 \ times 9-5 \ times 5-6 \ times 3 {\ big |} \\ [10pt] & = { 60 \ over 2} = 30. \ End {alinhado}}}$

Etimologia

A razão pela qual essa fórmula é chamada de fórmula do cadarço é devido a um método comum usado para avaliá-la. Este método usa matrizes . Como exemplo, escolha o triângulo com vértices (2, 4), (3, −8) e (1, 2). Em seguida, construa a matriz a seguir “andando ao redor” do triângulo e terminando com o ponto inicial.

${\ displaystyle {\ begin {bmatrix} 2 & 4 \\ 3 & -8 \\ 1 & 2 \\ 2 & 4 \ end {bmatrix}}}$

Primeiro, desenhe diagonal para baixo e para as barras direitas (como mostrado abaixo),

  

e multiplique os dois números conectados por cada barra, então some todos os produtos: (2 × −8) + (3 × 2) + (1 × 4) = −6. Faça a mesma coisa com barras diagonais para baixo e para a esquerda (mostrado abaixo com barras para baixo):

  

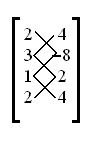
(4 × 3) + (−8 × 1) + (2 × 2) = 8. Então tome a diferença absoluta desses dois números: | (−6) - (8) | = 14. Reduzir pela metade resulta a área do triângulo: 7. Organizar os números desta forma torna a fórmula mais fácil de lembrar e avaliar. Com todas as barras desenhadas, a matriz lembra vagamente um sapato com os cadarços arrumados, dando origem ao nome do algoritmo.

Generalização

Em dimensões superiores, a área de um polígono pode ser calculada a partir de seus vértices usando a forma de álgebra externa da fórmula do cadarço (por exemplo, em 3d, a soma de produtos cruzados sucessivos ):

(quando os vértices não são coplanares, isso calcula a área do vetor delimitada pelo loop, ou seja, a área projetada ou "sombra" no plano em que é maior).

Esta formulação também pode ser generalizada para calcular o volume de um politopo n-dimensional a partir das coordenadas de seus vértices, ou mais precisamente, de sua malha hipersuperficial . Por exemplo, o volume de um poliedro tridimensional pode ser encontrado triangulando sua malha de superfície e somando os volumes assinados dos tetraedros formados por cada triângulo de superfície e a origem:

$${\ displaystyle V = {\ frac {1} {6}} \ left \ | \ sum _ {F} v_ {a} \ wedge v_ {b} \ wedge v_ {c} \ right \ |}$$

onde a soma está sobre as faces e deve-se tomar cuidado para ordenar os vértices de forma consistente (todos no sentido horário ou anti-horário vistos de fora do poliedro). Alternativamente, uma expressão em termos das áreas da face e normais da superfície pode ser derivada usando o teorema da divergência (ver Poliedro § Volume ).

Veja também

• Planímetro
• Teorema de Pick
• Fórmula de garça

links externos

• Vídeo do Mathologer sobre a fórmula do cadarço de Gauss

Referências