Distribuição estável - Stable distribution

Estábulo

Função densidade de probabilidade Distribuições simétricas α- estáveis ​​com fator de escala unitário Distribuições estáveis ​​centradas enviesadas com fator de escala unitário
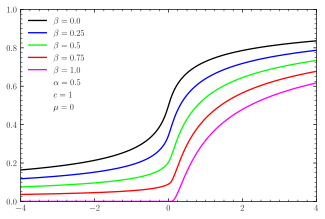
Função de distribuição cumulativa CDFs para distribuições simétricas α- estáveis CDFs para distribuições estáveis ​​centradas enviesadas
Parâmetros	α ∈ (0, 2] - parâmetro de estabilidade β ∈ [−1, 1] - parâmetro de assimetria (observe que a assimetria é indefinida) c ∈ (0, ∞) - parâmetro de escala μ ∈ (−∞, ∞) - parâmetro de localização
Apoio, suporte	x ∈ [ μ , + ∞) se α <1 e β = 1 x ∈ (-∞, μ ] se α <1 e β = −1 x ∈ R caso contrário
PDF	não expressável analiticamente, exceto para alguns valores de parâmetro
CDF	não expressável analiticamente, exceto para certos valores de parâmetros
Quer dizer	μ quando α > 1 , caso contrário, indefinido
Mediana	μ quando β = 0 , caso contrário, não expressável analiticamente
Modo	μ quando β = 0 , caso contrário, não expressável analiticamente
Variância	2 c 2 quando α = 2 , caso contrário, infinito
Skewness	0 quando α = 2 , caso contrário, indefinido
Ex. curtose	0 quando α = 2 , caso contrário, indefinido
Entropia	não expressável analiticamente, exceto para certos valores de parâmetros
MGF	${\ displaystyle \ exp \! \ left (t \ mu + c ^ {2} t ^ {2} \ right)}$quando , caso contrário, indefinido${\ displaystyle \ alpha = 2}$
CF	${\ displaystyle \ exp \! {\ Big [} \; it \ mu - | c \, t | ^ {\ alpha} \, (1-i \ beta \ operatorname {sgn} (t) \ Phi) \; {\Grande ]},}$ Onde ${\ displaystyle \ Phi = {\ begin {cases} \ tan {\ tfrac {\ pi \ alpha} {2}} & {\ text {if}} \ alpha \ neq 1 \\ - {\ tfrac {2} { \ pi}} \ log | c \, t | & {\ text {if}} \ alpha = 1 \ end {cases}}}$

Na teoria da probabilidade , uma distribuição é considerada estável se uma combinação linear de duas variáveis ​​aleatórias independentes com esta distribuição tem a mesma distribuição, até os parâmetros de localização e escala . Uma variável aleatória é considerada estável se sua distribuição for estável. A família de distribuição estável também é algumas vezes chamada de distribuição Lévy alfa-estável , em homenagem a Paul Lévy , o primeiro matemático a estudá-la.

Dos quatro parâmetros que definem a família, a maior atenção foi focada no parâmetro de estabilidade, α (consulte o painel). Distribuições estáveis ​​têm 0 < α ≤ 2 , com o limite superior correspondendo à distribuição normal e α = 1 à distribuição de Cauchy . As distribuições têm variância indefinida para α <2 e média indefinida para α ≤ 1 . A importância das distribuições de probabilidade estáveis ​​é que elas são " atratores " para somas devidamente normalizadas de variáveis ​​aleatórias independentes e distribuídas de forma idêntica ( iid ). A distribuição normal define uma família de distribuições estáveis. Pelo teorema do limite central clássico, a soma devidamente normalizada de um conjunto de variáveis ​​aleatórias, cada uma com variância finita, tenderá a uma distribuição normal à medida que o número de variáveis ​​aumenta. Sem a suposição de variância finita, o limite pode ser uma distribuição estável que não é normal. Mandelbrot se referiu a essas distribuições como "distribuições paretianas estáveis", em homenagem a Vilfredo Pareto . Em particular, ele se referiu àquelas distorcidas ao máximo na direção positiva com 1 < α <2 como "distribuições de Pareto-Lévy", que ele considerou como melhores descrições dos preços de ações e commodities do que as distribuições normais.

Definição

Uma distribuição não degenerada é uma distribuição estável se satisfizer a seguinte propriedade:

Deixe que X ₁ e X ₂ cópias ser independente de uma variável aleatória X . Então X é dito para ser estável se por quaisquer constantes de um > 0 e b > 0 a variável aleatória aX ₁ + bX ₂ tem a mesma distribuição que cX + d para algumas constantes c > 0 e d . A distribuição é considerada estritamente estável se for mantida com d = 0 .

Como a distribuição normal , a distribuição de Cauchy e a distribuição de Lévy possuem a propriedade acima, segue-se que são casos especiais de distribuições estáveis.

Essas distribuições formam uma família de quatro parâmetros de distribuições de probabilidade contínuas parametrizadas por parâmetros de localização e escala μ e c , respectivamente, e dois parâmetros de forma β e α , correspondendo aproximadamente a medidas de assimetria e concentração, respectivamente (ver as figuras).

A função característica φ ( t ) de qualquer distribuição de probabilidade é apenas a transformada de Fourier de sua função de densidade de probabilidade f ( x ). A função densidade é, portanto, a transformada de Fourier inversa da função característica.

${\ displaystyle f (x) = {\ frac {1} {2 \ pi}} \ int _ {- \ infty} ^ {\ infty} \ varphi (t) e ^ {- ixt} \, dt}$

Embora a função de densidade de probabilidade para uma distribuição geral estável não possa ser escrita analiticamente, a função característica geral pode ser expressa analiticamente. Uma variável aleatória X é chamada de estável se sua função característica pode ser escrita como

${\ displaystyle \ varphi (t; \ alpha, \ beta, c, \ mu) = \ exp \ left (it \ mu - | ct | ^ {\ alpha} \ left (1-i \ beta \ operatorname {sgn} (t) \ Phi \ right) \ right)}$

onde sgn ( t ) é apenas o sinal de t e

${\ displaystyle \ Phi = {\ begin {cases} \ tan \ left ({\ frac {\ pi \ alpha} {2}} \ right) & \ alpha \ neq 1 \\ - {\ frac {2} {\ pi}} \ log | ct | & \ alpha = 1 \ end {casos}}}$

μ ∈ R é um parâmetro de deslocamento, β ∈ [−1, 1], chamado de parâmetro de assimetria , é uma medida de assimetria. Note que neste contexto a assimetria usual não está bem definida, já que para α <2 a distribuição não admite segundos momentos ou maiores , e a definição usual de assimetria é o terceiro momento central .

A razão pela qual isso dá uma distribuição estável é que a função característica para a soma de duas variáveis ​​aleatórias independentes é igual ao produto das duas funções características correspondentes. Adicionar duas variáveis ​​aleatórias de uma distribuição estável dá algo com os mesmos valores de α e β , mas possivelmente valores diferentes de μ e c .

Nem toda função é a função característica de uma distribuição de probabilidade legítima (isto é, aquela cuja função de distribuição cumulativa é real e vai de 0 a 1 sem diminuir), mas as funções características dadas acima serão legítimas, desde que os parâmetros estejam em seus gamas. O valor da função característica em algum valor t é o conjugado complexo de seu valor em - t, como deveria ser para que a função de distribuição de probabilidade seja real.

No caso mais simples β = 0 , a função característica é apenas uma função exponencial esticada ; a distribuição é simétrica em relação a μ e é referida como uma distribuição alfa-estável simétrica (Lévy) , frequentemente abreviada como SαS .

Quando α <1 e β = 1, a distribuição é suportada por [ μ , ∞).

O parâmetro c > 0 é um fator de escala que é uma medida da largura da distribuição, enquanto α é o expoente ou índice da distribuição e especifica o comportamento assintótico da distribuição.

Parametrizações

A definição acima é apenas uma das parametrizações em uso para distribuições estáveis; é o mais comum, mas não é contínuo nos parâmetros em α = 1 .

Uma parametrização contínua é

${\ displaystyle \ varphi (t; \ alpha, \ beta, \ gamma, \ delta) = \ exp \ left (it \ delta - | \ gamma t | ^ {\ alpha} \ left (1-i \ beta \ operatorname {sgn} (t) \ Phi \ right) \ right)}$

Onde:

${\ displaystyle \ Phi = {\ begin {cases} \ left (| \ gamma t | ^ {1- \ alpha} -1 \ right) \ tan \ left ({\ tfrac {\ pi \ alpha} {2}} \ direita) & \ alpha \ neq 1 \\ - {\ frac {2} {\ pi}} \ log | \ gamma t | & \ alpha = 1 \ end {casos}}}$

Os intervalos de α e β são os mesmos de antes, γ (como c ) deve ser positivo e δ (como μ ) deve ser real.

Em qualquer parametrização, pode-se fazer uma transformação linear da variável aleatória para obter uma variável aleatória cuja densidade é . Na primeira parametrização, isso é feito definindo a nova variável: ${\ displaystyle f (y; \ alpha, \ beta, 1,0)}$

${\ displaystyle y = {\ begin {cases} {\ frac {x- \ mu} {\ gamma}} & \ alpha \ neq 1 \\ {\ frac {x- \ mu} {\ gamma}} - \ beta {\ frac {2} {\ pi}} \ ln \ gamma & \ alpha = 1 \ end {casos}}}$

Para a segunda parametrização, simplesmente usamos

${\ displaystyle y = {\ frac {x- \ delta} {\ gamma}}}$

não importa o que é α . Na primeira parametrização, se a média existe (ou seja, α > 1 ) então ela é igual a μ , enquanto na segunda parametrização, quando a média existe, ela é igual a${\ displaystyle \ delta - \ beta \ gamma \ tan \ left ({\ tfrac {\ pi \ alpha} {2}} \ right).}$

A distribuição

Uma distribuição estável é, portanto, especificada pelos quatro parâmetros acima. Pode ser mostrado que qualquer distribuição estável não degenerada tem uma função de densidade suave (infinitamente diferenciável). Se denota a densidade de X e Y é a soma das cópias independentes de X : ${\ displaystyle f (x; \ alpha, \ beta, c, \ mu)}$

${\ displaystyle Y = \ sum _ {i = 1} ^ {N} k_ {i} (X_ {i} - \ mu) \,}$

então Y tem a densidade com ${\ displaystyle {\ tfrac {1} {s}} f (y / s; \ alpha, \ beta, c, 0)}$

${\ displaystyle s = \ left (\ sum _ {i = 1} ^ {N} | k_ {i} | ^ {\ alpha} \ right) ^ {\ frac {1} {\ alpha}}}$

O comportamento assintótico é descrito, para α <2, por:

${\ displaystyle f (x) \ sim {\ frac {1} {| x | ^ {1+ \ alpha}}} \ left (c ^ {\ alpha} (1+ \ operatorname {sgn} (x) \ beta ) \ sin \ left ({\ frac {\ pi \ alpha} {2}} \ right) {\ frac {\ Gamma (\ alpha +1)} {\ pi}} \ right)}$

onde Γ é a função Gamma (exceto quando α ≥ 1 e β = ± 1, a cauda não desaparece para a esquerda ou direita, respectivamente, de μ , embora a expressão acima seja 0). Este comportamento de " cauda pesada " faz com que a variância das distribuições estáveis ​​seja infinita para todos α <2. Esta propriedade é ilustrada nos gráficos log – log abaixo.

Quando α = 2, a distribuição é Gaussiano (ver abaixo), com as caudas para assimptóticas exp (- x ² /4 c ² ) / (2 c √π).

Distribuição estável unilateral e distribuição estável de contagem

Quando α <1 e β = 1, a distribuição é suportada por [ μ , ∞). Esta família é chamada de distribuição estável unilateral . Sua distribuição padrão (μ = 0) é definida como

${\ displaystyle L _ {\ alpha} (x) = f \ left (x; \ alpha, 1, \ cos \ left ({\ frac {\ alpha \ pi} {2}} \ right) ^ {1 / \ alpha }, 0 \ right)}$, onde .${\ displaystyle \ alpha <1}$

Deixe , sua função característica é . Assim, a forma integral de seu PDF é (nota :) ${\ displaystyle q = \ exp (-i \ alpha \ pi / 2)}$${\ displaystyle \ varphi (t; \ alpha) = \ exp \ left (-q | t | ^ {\ alpha} \ right)}$${\ displaystyle {\ text {Im}} (q) <0}$

${\ displaystyle {\ begin {alinhados} L _ {\ alpha} (x) & = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {- \ infty} ^ {\ infty} e ^ {itx} e ^ {- q | t | ^ {\ alpha}} \, dt \ right] \\ & = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ infty} e ^ {- {\ text {Re}} (q) \, t ^ {\ alpha}} \ sin (tx) \ sin (- {\ text {Im}} (q) \, t ^ {\ alpha}) \, dt, {\ text {or}} \\ & = {\ frac {2} {\ pi}} \ int _ {0} ^ {\ infty} e ^ {- {\ text {Re}} (q ) \, t ^ {\ alpha}} \ cos (tx) \ cos ({\ text {Im}} (q) \, t ^ {\ alpha}) \, dt. \\\ end {alinhado}}}$

A integral de seno duplo é mais eficaz para muito pequenos . ${\ displaystyle x}$

Considere a soma de Lévy onde , então Y tem a densidade onde . Definido , chegamos à distribuição de contagem estável . Sua distribuição padrão é definida como ${\ displaystyle Y = \ sum _ {i = 1} ^ {N} X_ {i}}$${\ displaystyle X_ {i} \ sim L _ {\ alpha} (x)}$${\ displaystyle {\ frac {1} {\ nu}} L _ {\ alpha} \ left ({\ frac {x} {\ nu}} \ right)}$${\ displaystyle \ nu = N ^ {1 / \ alpha}}$${\ displaystyle x = 1}$

${\ displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu) = {\ frac {\ alpha} {\ Gamma \ left ({\ frac {1} {\ alpha}} \ right)}} { \ frac {1} {\ nu}} L _ {\ alpha} \ left ({\ frac {1} {\ nu}} \ right)}$, onde e .${\ displaystyle \ nu> 0}$${\ displaystyle \ alpha <1}$

A distribuição de contagem estável é o conjugado anterior à distribuição estável unilateral. Sua família de escala de localização é definida como

${\ displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu; \ nu _ {0}, \ theta) = {\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha }})}} {\ frac {1} {\ nu - \ nu _ {0}}} L _ {\ alpha} \ left ({\ frac {\ theta} {\ nu - \ nu _ {0}}} \direito)}$, Em que , e .${\ displaystyle \ nu> \ nu _ {0}}$${\ displaystyle \ theta> 0}$${\ displaystyle \ alpha <1}$

É também uma distribuição unilateral suportada por . O parâmetro de localização é o local de corte, enquanto define sua escala. ${\ displaystyle [\ nu _ {0}, \ infty)}$${\ displaystyle \ nu _ {0}}$${\ displaystyle \ theta}$

Quando , é a distribuição de Lévy, que é uma distribuição gama inversa. Assim, é uma distribuição gama deslocada de forma 3/2 e escala , ${\ displaystyle \ alpha = {\ frac {1} {2}}}$${\ displaystyle L _ {\ frac {1} {2}} (x)}$${\ displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta)}$${\ displaystyle 4 \ theta}$

${\ displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta) = {\ frac {1} {4 {\ sqrt {\ pi }} \ theta ^ {3/2}}} (\ nu - \ nu _ {0}) ^ {1/2} e ^ {- {\ frac {\ nu - \ nu _ {0}} {4 \ theta}}}}$, Onde , .${\ displaystyle \ nu> \ nu _ {0}}$${\ displaystyle \ theta> 0}$

Sua média é e seu desvio padrão é . É hipotetizado que o VIX é distribuído como com e (consulte a seção 7 de). Assim, a distribuição de contagem estável é a distribuição marginal de primeira ordem de um processo de volatilidade. Nesse contexto, é denominado “piso de volatilidade”. ${\ displaystyle \ nu _ {0} +6 \ theta}$${\ displaystyle {\ sqrt {24}} \ theta}$${\ displaystyle {\ mathfrak {N}} _ {\ frac {1} {2}} (\ nu; \ nu _ {0}, \ theta)}$${\ displaystyle \ nu _ {0} = 10,4}$${\ displaystyle \ theta = 1.6}$${\ displaystyle \ nu _ {0}}$

Outra abordagem para derivar a distribuição de contagem estável é usar a transformada de Laplace da distribuição estável unilateral, (Seção 2.4 de)

${\ displaystyle \ int _ {0} ^ {\ infty} e ^ {- zx} L _ {\ alpha} (x) dx = e ^ {- z ^ {\ alpha}}}$, onde .${\ displaystyle \ alpha <1}$

Vamos , e pode-se decompor a integral no lado esquerdo como uma distribuição de produto de uma distribuição de Laplace padrão e uma distribuição de contagem estável padrão, ${\ displaystyle x = 1 / \ nu}$

${\ displaystyle \ int _ {0} ^ {\ infty} {\ frac {1} {\ nu}} \ left ({\ frac {1} {2}} e ^ {- {\ frac {| z |} {\ nu}}} \ right) \ left ({\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha}})}} {\ frac {1} {\ nu}} L_ { \ alpha} ({\ frac {1} {\ nu}}) \ right) d \ nu = {\ frac {1} {2}} {\ frac {\ alpha} {\ Gamma ({\ frac {1} {\ alpha}})}} e ^ {- | z | ^ {\ alpha}}}$, onde .${\ displaystyle \ alpha <1}$

Isso é chamado de "decomposição lambda" (consulte a Seção 4 de), uma vez que o lado direito foi nomeado como "distribuição lambda simétrica" ​​nos trabalhos anteriores de Lihn. No entanto, ele tem vários nomes mais populares, como " distribuição de potência exponencial " ou "erro generalizado / distribuição normal", frequentemente referido quando α > 1.

O enésimo momento de é o -ésimo momento de , Todos os momentos positivos são finitos. Isso de certa forma resolve o problema espinhoso dos momentos divergentes na distribuição estável. ${\ displaystyle {\ mathfrak {N}} _ {\ alpha} (\ nu)}$${\ displaystyle - (n + 1)}$${\ displaystyle L _ {\ alpha} (x)}$

Propriedades

• Todas as distribuições estáveis ​​são infinitamente divisíveis .
• Com exceção da distribuição normal ( α = 2), as distribuições estáveis ​​são leptocurtóticas e distribuições de cauda pesada .
• Fechamento sob convolução

Distribuições estáveis ​​são fechadas sob convolução para um valor fixo de α . Visto que a convolução é equivalente à multiplicação da função transformada de Fourier, segue-se que o produto de duas funções características estáveis ​​com o mesmo α produzirá outra função característica. O produto de duas funções características estáveis ​​é dado por:

${\ displaystyle \ exp \ left (it \ mu _ {1} + it \ mu _ {2} - | c_ {1} t | ^ {\ alpha} - | c_ {2} t | ^ {\ alpha} + i \ beta _ {1} | c_ {1} t | ^ {\ alpha} \ operatorname {sgn} (t) \ Phi + i \ beta _ {2} | c_ {2} t | ^ {\ alpha} \ operatorname {sgn} (t) \ Phi \ right)}$

Uma vez que Φ não é uma função das variáveis μ , c ou β, segue-se que esses parâmetros para a função convolvida são dados por:

${\ displaystyle {\ begin {alinhados} \ mu & = \ mu _ {1} + \ mu _ {2} \\ | c | & = \ left (| c_ {1} | ^ {\ alpha} + | c_ {2} | ^ {\ alpha} \ right) ^ {\ frac {1} {\ alpha}} \\ [6pt] \ beta & = {\ frac {\ beta _ {1} | c_ {1} | ^ {\ alpha} + \ beta _ {2} | c_ {2} | ^ {\ alpha}} {| c_ {1} | ^ {\ alpha} + | c_ {2} | ^ {\ alpha}}} \ fim {alinhado}}}$

Em cada caso, pode ser mostrado que os parâmetros resultantes estão dentro dos intervalos necessários para uma distribuição estável.

Um teorema do limite central generalizado

Outra propriedade importante das distribuições estáveis ​​é o papel que desempenham em um teorema do limite central generalizado . O teorema do limite central afirma que a soma de um número de variáveis ​​aleatórias independentes e identicamente distribuídas (iid) com variâncias finitas diferentes de zero tenderá a uma distribuição normal à medida que o número de variáveis ​​aumenta.

Uma generalização devida a Gnedenko e Kolmogorov afirma que a soma de um número de variáveis ​​aleatórias com distribuições simétricas tendo caudas de lei de potência ( caudas paretianas ), diminuindo conforme onde (e, portanto, tendo variância infinita), tenderá a uma distribuição estável como o número de summands cresce. Se, então, a soma converge para uma distribuição estável com parâmetro de estabilidade igual a 2, ou seja, uma distribuição Gaussiana. ${\ displaystyle | x | ^ {- \ alpha -1}}$${\ displaystyle 0 <\ alpha \ leqslant 2}$${\ displaystyle f (x; \ alpha, 0, c, 0)}$${\ displaystyle \ alpha> 2}$

Existem outras possibilidades também. Por exemplo, se a função característica da variável aleatória é assintótica para t pequeno (positivo ou negativo), então podemos perguntar como t varia com n quando o valor da função característica para a soma de n tais variáveis ​​aleatórias é igual a um dado valoriza você : ${\ displaystyle 1 + a | t | ^ {\ alpha} \ ln | t |}$

${\ displaystyle \ varphi _ {\ text {sum}} = \ varphi ^ {n} = u}$

Assumindo por enquanto que t → 0, tomamos o limite do acima como n → ∞ :

${\ displaystyle \ ln u = \ lim _ {n \ to \ infty} n \ ln \ varphi = \ lim _ {n \ to \ infty} na | t | ^ {\ alpha} \ ln | t |.}$

Portanto:

${\ displaystyle {\ begin {alinhados} \ ln (\ ln u) & = \ ln \ left (\ lim _ {n \ to \ infty} na | t | ^ {\ alpha} \ ln | t | \ right) \\ [5pt] & = \ lim _ {n \ a \ infty} \ ln \ left (na | t | ^ {\ alpha} \ ln | t | \ right) = \ lim _ {n \ a \ infty} \ left \ {\ ln (na) + \ alpha \ ln | t | + \ ln (\ ln | t |) \ right \} \ end {alinhado}}}$

Isso mostra que é assintótico ao usar a equação anterior que temos ${\ displaystyle \ ln | t |}$${\ displaystyle {\ tfrac {-1} {\ alpha}} \ ln n,}$

${\ displaystyle | t | \ sim \ left ({\ frac {- \ alpha \ ln u} {na \ ln n}} \ right) ^ {1 / \ alpha}.}$

Isso implica que a soma dividida por

${\ displaystyle \ left ({\ frac {na \ ln n} {\ alpha}} \ right) ^ {\ frac {1} {\ alpha}}}$

tem uma função característica cujo valor em algum t ′ vai para u (conforme n aumenta) quando Em outras palavras, a função característica converge pontualmente para e, portanto, pelo teorema da continuidade de Lévy a soma dividida por ${\ displaystyle t '= (- \ ln u) ^ {\ frac {1} {\ alpha}}.}$${\ displaystyle \ exp (- (t ') ^ {\ alpha})}$

${\ displaystyle \ left ({\ frac {na \ ln n} {\ alpha}} \ right) ^ {\ frac {1} {\ alpha}}}$

converge em distribuição para a distribuição alfa-estável simétrica com parâmetro de estabilidade e parâmetro de escala 1. ${\ displaystyle \ alpha}$

Isso pode ser aplicado a uma variável aleatória cujas caudas diminuem como . Essa variável aleatória tem uma média, mas a variância é infinita. Vamos fazer a seguinte distribuição: ${\ displaystyle | x | ^ {- 3}}$

${\ displaystyle f (x) = {\ begin {cases} {\ frac {1} {3}} & | x | \ leqslant 1 \\ {\ frac {1} {3}} x ^ {- 3} & | x |> 1 \ end {casos}}}$

Podemos escrever isso como

${\ displaystyle f (x) = \ int _ {1} ^ {\ infty} {\ frac {2} {w ^ {4}}} h \ left ({\ frac {x} {w}} \ right) dw}$

Onde

${\ displaystyle h \ left ({\ frac {x} {w}} \ right) = {\ begin {cases} {\ frac {1} {2}} & \ left | {\ frac {x} {w} } \ right | <1, \\ 0 & \ left | {\ frac {x} {w}} \ right |> 1. \ end {cases}}}$

Queremos encontrar os termos principais da expansão assintótica da função característica. A função característica da distribuição de probabilidade é então a função característica para f ( x ) é ${\ displaystyle {\ tfrac {1} {w}} h \ left ({\ tfrac {x} {w}} \ right)}$${\ displaystyle {\ tfrac {\ sin (tw)} {tw}},}$

${\ displaystyle \ varphi (t) = \ int _ {1} ^ {\ infty} {\ frac {2 \ sin (tw)} {tw ^ {4}}} dw}$

e podemos calcular:

${\ displaystyle {\ begin {align} \ varphi (t) -1 & = \ int _ {1} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] \, dw \\ & = \ int _ {1} ^ {\ frac {1} {| t |}} {\ frac {2} {w ^ { 3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] \, dw + \ int _ {\ frac {1} {| t |}} ^ {\ infty} { \ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] \, dw \\ & = \ int _ {1} ^ { \ frac {1} {| t |}} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1+ \ left \ {- {\ frac {t ^ {2} w ^ {2}} {3!}} + {\ frac {t ^ {2} w ^ {2}} {3!}} \ right \} \ right] \, dw + \ int _ {\ frac {1} {| t |}} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw }} - 1 \ right] \, dw \\ & = \ int _ {1} ^ {\ frac {1} {| t |}} - {\ frac {t ^ {2} dw} {3w}} + \ int _ {1} ^ {\ frac {1} {| t |}} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} -1 + {\ frac {t ^ {2} w ^ {2}} {3!}} \ Right] dw + \ int _ {\ frac {1} {| t |}} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 \ right] dw \\ & = \ int _ {1} ^ {\ frac {1 } {| t |}} - {\ frac {t ^ {2} dw} {3w}} + \ left \ {\ int _ {0} ^ {\ frac {1} {| t |}} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {3!} } \ right] dw- \ int _ {0} ^ {1} {\ frac {2} {w ^ {3 }}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {3!}} \ right] dw \ right \ } + \ int _ {\ frac {1} {| t |}} ^ {\ infty} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} { tw}} - 1 \ right] dw \\ & = \ int _ {1} ^ {\ frac {1} {| t |}} - {\ frac {t ^ {2} dw} {3w}} + t ^ {2} \ int _ {0} ^ {1} {\ frac {2} {y ^ {3}}} \ left [{\ frac {\ sin (y)} {y}} - 1 + {\ frac {y ^ {2}} {6}} \ right] dy- \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {6}} \ right] dw + t ^ {2} \ int _ {1} ^ {\ infty } {\ frac {2} {y ^ {3}}} \ left [{\ frac {\ sin (y)} {y}} - 1 \ right] dy \\ & = - {\ frac {t ^ { 2}} {3}} \ int _ {1} ^ {\ frac {1} {| t |}} {\ frac {dw} {w}} + t ^ {2} C_ {1} - \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {6}} \ right] dw + t ^ {2} C_ {2} \\ & = {\ frac {t ^ {2}} {3}} \ ln | t | + t ^ {2} C_ {3} - \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {\ sin (tw)} {tw}} - 1 + {\ frac {t ^ {2} w ^ {2}} {6}} \ right] dw \\ & = {\ frac {t ^ {2}} {3}} \ ln | t | + t ^ {2} C_ {3} - \ int _ {0} ^ {1} {\ frac {2} {w ^ {3}}} \ left [{\ frac {t ^ {4} w ^ {4} } {5!}} + \ Cdots \ right] dw \\ & = {\ frac {t ^ {2}} {3}} \ ln | t | + t ^ {2} C_ {3} - {\ mathcal {O}} \ left (t ^ {4} \ right) \ end {al igned}}}$

onde e são constantes. Portanto, ${\ displaystyle C_ {1}, C_ {2}}$${\ displaystyle C_ {3}}$

${\ displaystyle \ varphi (t) \ sim 1 + {\ frac {t ^ {2}} {3}} \ ln | t |}$

e de acordo com o que foi dito acima (e o fato de que a variância de f ( x ; 2,0,1,0) é 2), a soma de n instâncias desta variável aleatória, dividida por convergirá na distribuição para um Gaussiano distribuição com variância 1. Mas a variância em qualquer n particular ainda será infinita. Observe que a largura da distribuição limite cresce mais rápido do que no caso em que a variável aleatória tem uma variância finita (nesse caso, a largura cresce como a raiz quadrada de n ). A média , obtida pela divisão da soma por n , tende a um gaussiano cuja largura se aproxima de zero à medida que n aumenta, de acordo com a Lei dos grandes números . ${\ displaystyle {\ sqrt {n (\ ln n) / 12}},}$

Casos especiais

Gráfico log-log de PDFs de distribuição estável centrada simétrica mostrando o comportamento da lei de potência para x grande . O comportamento da lei de potência é evidenciado pela aparência em linha reta da PDF para x grande , com a inclinação igual a - ( α + 1). (A única exceção é para α = 2, em preto, que é uma distribuição normal.)

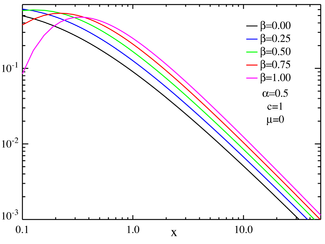
Gráfico log-log de PDFs de distribuição estáveis ​​centralizados enviesados ​​mostrando o comportamento da lei de potência para x grande . Mais uma vez, a inclinação das porções lineares é igual a - ( α + 1)

Não há solução analítica geral para a forma de f ( x ). Existem, no entanto, três casos especiais que podem ser expressos em termos de funções elementares, como pode ser visto pela inspeção da função característica :

• Para α = 2, a distribuição se reduz a uma distribuição gaussiana com variância σ ² = 2 c ² e média μ ; o parâmetro de assimetria β não tem efeito.
• Para α = 1 e β = 0, a distribuição se reduz a uma distribuição de Cauchy com parâmetro de escala ce parâmetro de deslocamento µ .
• Para α = 1/2 e β = 1, a distribuição se reduz a uma distribuição de Lévy com parâmetro de escala ce parâmetro de deslocamento µ .

Observe que as três distribuições acima também estão conectadas, da seguinte maneira: Uma variável aleatória padrão de Cauchy pode ser vista como uma mistura de variáveis ​​aleatórias Gaussianas (todas com média zero), com a variância sendo extraída de uma distribuição padrão de Lévy. E, de fato, este é um caso especial de um teorema mais geral (ver pág. 59 de) que permite que qualquer distribuição alfa-estável simétrica seja vista desta forma (com o parâmetro alfa da distribuição da mistura igual a duas vezes o parâmetro alfa de a distribuição de mistura - e o parâmetro beta da distribuição de mistura sempre igual a um).

Uma expressão de forma fechada geral para PDFs estáveis ​​com valores racionais de α está disponível em termos de funções G de Meijer . As funções Fox H também podem ser usadas para expressar as funções de densidade de probabilidade estáveis. Para números racionais simples, a expressão de forma fechada é freqüentemente em termos de funções especiais menos complicadas . Várias expressões de forma fechada com expressões bastante simples em termos de funções especiais estão disponíveis. Na tabela abaixo, os PDFs expressos por funções elementares são indicados por um E e aqueles que são expressos por funções especiais são indicados por um s .

Alguns dos casos especiais são conhecidos por nomes específicos:

• Para α = 1 e β = 1, a distribuição é uma distribuição de Landau que tem um uso específico em física com este nome.
• Para α = 3/2 e β = 0, a distribuição se reduz a uma distribuição de Holtsmark com parâmetro de escala ce parâmetro de deslocamento µ .

Além disso, no limite, à medida que c se aproxima de zero ou α se aproxima de zero, a distribuição se aproxima de uma função delta de Dirac δ ( x  -  μ ) .

Representação da série

A distribuição estável pode ser reafirmada como a parte real de uma integral mais simples:

${\ displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {0} ^ {\ infty} e ^ {it (x- \ mu)} e ^ {- (ct) ^ {\ alpha} (1-i \ beta \ Phi)} \, dt \ right].}$

Expressando a segunda exponencial como uma série de Taylor , temos:

${\ displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ int _ {0} ^ {\ infty} e ^ {it (x- \ mu)} \ sum _ {n = 0} ^ {\ infty} {\ frac {(-qt ^ {\ alpha}) ^ {n}} {n!}} \, dt \ right]}$

onde . Inverter a ordem de integração e somatório e realizar a integração resulta em: ${\ displaystyle q = c ^ {\ alpha} (1-i \ beta \ Phi)}$

${\ displaystyle f (x; \ alpha, \ beta, c, \ mu) = {\ frac {1} {\ pi}} \ Re \ left [\ sum _ {n = 1} ^ {\ infty} {\ frac {(-q) ^ {n}} {n!}} \ left ({\ frac {i} {x- \ mu}} \ right) ^ {\ alpha n + 1} \ Gamma (\ alpha n + 1) \ direita]}$

que será válido para x ≠ μ e convergirá para os valores apropriados dos parâmetros. (Observe que o termo n = 0 que produz uma função delta em x - µ foi, portanto, descartado.) Expressar a primeira exponencial como uma série produzirá outra série em potências positivas de x - µ que geralmente é menos útil.

Para distribuição estável unilateral, a expansão da série acima precisa ser modificada, uma vez que e . Não há nenhuma parte real a somar. Em vez disso, a integral da função característica deve ser realizada no eixo negativo, o que produz: ${\ displaystyle q = \ exp (-i \ alpha \ pi / 2)}$${\ displaystyle qi ^ {\ alpha} = 1}$

${\ displaystyle {\ begin {alinhados} L _ {\ alpha} (x) & = {\ frac {1} {\ pi}} \ Re \ left [\ sum _ {n = 1} ^ {\ infty} {\ frac {(-q) ^ {n}} {n!}} \ left ({\ frac {-i} {x}} \ right) ^ {\ alpha n + 1} \ Gamma (\ alpha n + 1) \ right] \\ & = {\ frac {1} {\ pi}} \ sum _ {n = 1} ^ {\ infty} {\ frac {- \ sin (n (\ alpha +1) \ pi)} {n!}} \ left ({\ frac {1} {x}} \ right) ^ {\ alpha n + 1} \ Gamma (\ alpha n + 1) \\\ end {alinhado}}}$

Simulação de variáveis ​​estáveis

Simular sequências de variáveis ​​aleatórias estáveis ​​não é simples, uma vez que não há expressões analíticas para o inverso nem para o próprio CDF . Todas as abordagens padrão, como a rejeição ou os métodos de inversão, exigiriam cálculos tediosos. Uma solução muito mais elegante e eficiente foi proposta por Chambers, Mallows and Stuck (CMS), que notou que uma determinada fórmula integral gerou o seguinte algoritmo: ${\ displaystyle F ^ {- 1} (x)}$${\ displaystyle F (x)}$

• gerar uma variável aleatória uniformemente distribuída e uma variável aleatória exponencial independente com média 1;${\ displaystyle U}$${\ displaystyle \ left (- {\ tfrac {\ pi} {2}}, {\ tfrac {\ pi} {2}} \ right)}$${\ displaystyle W}$
• para computação:${\ displaystyle \ alpha \ neq 1}$

${\ displaystyle X = \ left (1+ \ zeta ^ {2} \ right) ^ {\ frac {1} {2 \ alpha}} {\ frac {\ sin (\ alpha (U + \ xi))} {( \ cos (U)) ^ {\ frac {1} {\ alpha}}}} \ left ({\ frac {\ cos (U- \ alpha (U + \ xi))} {W}} \ right) ^ { \ frac {1- \ alpha} {\ alpha}},}$

• para computação:${\ displaystyle \ alpha = 1}$

${\ displaystyle X = {\ frac {1} {\ xi}} \ left \ {\ left ({\ frac {\ pi} {2}} + \ beta U \ right) \ tan U- \ beta \ log \ esquerda ({\ frac {{\ frac {\ pi} {2}} W \ cos U} {{\ frac {\ pi} {2}} + \ beta U}} \ direita) \ direita \},}$

Onde

${\ displaystyle \ zeta = - \ beta \ tan {\ frac {\ pi \ alpha} {2}}, \ qquad \ xi = {\ begin {cases} {\ frac {1} {\ alpha}} \ arctan ( - \ zeta) & \ alpha \ neq 1 \\ {\ frac {\ pi} {2}} & \ alpha = 1 \ end {casos}}}$

Este algoritmo produz uma variável aleatória . Para uma prova detalhada, consulte. ${\ displaystyle X \ sim S _ {\ alpha} (\ beta, 1,0)}$

Dadas as fórmulas para a simulação de uma variável aleatória estável padrão, podemos facilmente simular uma variável aleatória estável para todos os valores admissíveis dos parâmetros , , e usando a seguinte propriedade. Se então ${\ displaystyle \ alpha}$${\ displaystyle c}$${\ displaystyle \ beta}$${\ displaystyle \ mu}$${\ displaystyle X \ sim S _ {\ alpha} (\ beta, 1,0)}$

${\ displaystyle Y = {\ begin {cases} cX + \ mu & \ alpha \ neq 1 \\ cX + {\ frac {2} {\ pi}} \ beta c \ log c + \ mu & \ alpha = 1 \ end { casos}}}$

é . Para (e ) o método CMS se reduz à conhecida transformação de Box-Muller para a geração de variáveis ​​aleatórias Gaussianas . Muitas outras abordagens foram propostas na literatura, incluindo a aplicação das expansões das séries de Bergström e LePage, ver e, respectivamente. No entanto, o método CMS é considerado o mais rápido e preciso. ${\ displaystyle S _ {\ alpha} (\ beta, c, \ mu)}$${\ displaystyle \ alpha = 2}$${\ displaystyle \ beta = 0}$

Formulários

As distribuições estáveis ​​devem sua importância, tanto na teoria quanto na prática, à generalização do teorema do limite central para variáveis ​​aleatórias sem momentos de segunda (e possivelmente primeira) ordem e a auto-similaridade que a acompanha da família estável. Foi o aparente afastamento da normalidade, juntamente com a demanda por um modelo auto-semelhante para dados financeiros (ou seja, a forma da distribuição para as variações anuais dos preços dos ativos deve se assemelhar às variações dos preços diários ou mensais constituintes) que levou Benoît Mandelbrot a propor que os preços do algodão seguem uma distribuição alfa-estável com α igual a 1,7. As distribuições de Lévy são freqüentemente encontradas na análise de comportamento crítico e dados financeiros.

Eles também são encontrados na espectroscopia como uma expressão geral para uma linha espectral ampliada de pressão quase-estaticamente .

A distribuição de Lévy de eventos de tempo de espera de erupções solares (tempo entre eventos de erupções ) foi demonstrada para erupções solares de raios-X rígidos CGRO BATSE em dezembro de 2001. A análise da assinatura estatística de Lévy revelou que duas assinaturas de memória diferentes eram evidentes; um relacionado ao ciclo solar e o segundo cuja origem parece estar associada a uma localização ou combinação de efeitos localizados da região ativa solar.

Outros casos analíticos

Vários casos de distribuições estáveis ​​expressáveis ​​analiticamente são conhecidos. Deixe a distribuição estável ser expressa até então sabermos: ${\ displaystyle f (x; \ alpha, \ beta, c, \ mu)}$

• A distribuição de Cauchy é dada por${\ displaystyle f (x; 1,0,1,0).}$
• A distribuição Lévy é dada por${\ displaystyle f (x; {\ tfrac {1} {2}}, 1,1,0).}$
• A distribuição normal é dada por${\ displaystyle f (x; 2,0,1,0).}$
• Seja uma função Lommel , então:${\ displaystyle S _ {\ mu, \ nu} (z)}$

${\ displaystyle f \ left (x; {\ tfrac {1} {3}}, 0,1,0 \ right) = \ Re \ left ({\ frac {2e ^ {- {\ frac {i \ pi} {4}}}} {3 {\ sqrt {3}} \ pi}} {\ frac {1} {\ sqrt {x ^ {3}}}} S_ {0, {\ frac {1} {3} }} \ left ({\ frac {2e ^ {\ frac {i \ pi} {4}}} {3 {\ sqrt {3}}}} {\ frac {1} {\ sqrt {x}}} \ certo, certo)}$

• Deixe e denote os Integrais de Fresnel então:${\ displaystyle S (x)}$${\ displaystyle C (x)}$

${\ displaystyle f \ left (x; {\ tfrac {1} {2}}, 0,1,0 \ right) = {\ frac {1} {\ sqrt {2 \ pi | x | ^ {3}} }} \ left (\ sin \ left ({\ tfrac {1} {4 | x |}} \ right) \ left [{\ frac {1} {2}} - S \ left ({\ tfrac {1} {\ sqrt {2 \ pi | x |}}} \ right) \ right] + \ cos \ left ({\ tfrac {1} {4 | x |}} \ right) \ left [{\ frac {1} {2}} - C \ left ({\ tfrac {1} {\ sqrt {2 \ pi | x |}}} \ right) \ right] \ right)}$

• Seja a função de Bessel modificada de segundo tipo então:${\ displaystyle K_ {v} (x)}$

${\ displaystyle f \ left (x; {\ tfrac {1} {3}}, 1,1,0 \ right) = {\ frac {1} {\ pi}} {\ frac {2 {\ sqrt {2 }}} {3 ^ {\ frac {7} {4}}}} {\ frac {1} {\ sqrt {x ^ {3}}}} K _ {\ frac {1} {3}} \ left ( {\ frac {4 {\ sqrt {2}}} {3 ^ {\ frac {9} {4}}}} {\ frac {1} {\ sqrt {x}}} \ right)}$

• Se o denotar as funções hipergeométricas, então:${\ displaystyle {} _ {m} F_ {n}}$

${\ displaystyle {\ begin {alinhados} f \ left (x; {\ tfrac {4} {3}}, 0,1,0 \ right) & = {\ frac {3 ^ {\ frac {5} {4 }}} {4 {\ sqrt {2 \ pi}}}} {\ frac {\ Gamma \ left ({\ tfrac {7} {12}} \ right) \ Gamma \ left ({\ tfrac {11} { 12}} \ right)} {\ Gamma \ left ({\ tfrac {6} {12}} \ right) \ Gamma \ left ({\ tfrac {8} {12}} \ right)}} {} _ { 2} F_ {2} \ left ({\ tfrac {7} {12}}, {\ tfrac {11} {12}}; {\ tfrac {6} {12}}, {\ tfrac {8} {12 }}; {\ tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} \ right) - {\ frac {3 ^ {\ frac {11} {4}} x ^ {3 }} {4 ^ {3} {\ sqrt {2 \ pi}}}} {\ frac {\ Gamma \ left ({\ tfrac {13} {12}} \ right) \ Gamma \ left ({\ tfrac { 17} {12}} \ right)} {\ Gamma \ left ({\ tfrac {18} {12}} \ right) \ Gamma \ left ({\ tfrac {15} {12}} \ right)}} { } _ {2} F_ {2} \ left ({\ tfrac {13} {12}}, {\ tfrac {17} {12}}; {\ tfrac {18} {12}}, {\ tfrac {15 } {12}}; {\ tfrac {3 ^ {3} x ^ {4}} {4 ^ {4}}} \ right) \\ [6pt] f \ left (x; {\ tfrac {3} { 2}}, 0,1,0 \ right) & = {\ frac {\ Gamma \ left ({\ tfrac {5} {3}} \ right)} {\ pi}} {} _ {2} F_ { 3} \ left ({\ tfrac {5} {12}}, {\ tfrac {11} {12}}; {\ tfrac {1} {3}}, {\ tfrac {1} {2}}, { \ tfrac {5} {6}}; - {\ tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} \ right) - {\ frac {x ^ {2}} {3 \ pi}} {} _ {3} F_ {4} \ l eft ({\ tfrac {3} {4}}, 1, {\ tfrac {5} {4}}; {\ tfrac {2} {3}}, {\ tfrac {5} {6}}, {\ tfrac {7} {6}}, {\ tfrac {4} {3}}; - {\ tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} \ right) + {\ frac {7x ^ {4} \ Gamma \ left ({\ tfrac {4} {3}} \ right)} {3 ^ {4} \ pi ^ {2}}} {} _ {2} F_ {3} \ left ({\ tfrac {13} {12}}, {\ tfrac {19} {12}}; {\ tfrac {7} {6}}, {\ tfrac {3} {2}}, {\ tfrac {5} {3}}; - {\ tfrac {2 ^ {2} x ^ {6}} {3 ^ {6}}} \ direita) \ end {alinhado}}}$

sendo a última a distribuição Holtsmark .

• Seja uma função Whittaker , então:${\ displaystyle W_ {k, \ mu} (z)}$

${\ displaystyle {\ begin {alinhados} f \ left (x; {\ tfrac {2} {3}}, 0,1,0 \ right) & = {\ frac {\ sqrt {3}} {6 {\ sqrt {\ pi}} | x |}} \ exp \ left ({\ tfrac {2} {27}} x ^ {- 2} \ right) W _ {- {\ frac {1} {2}}, { \ frac {1} {6}}} \ left ({\ tfrac {4} {27}} x ^ {- 2} \ right) \\ [8pt] f \ left (x; {\ tfrac {2} { 3}}, 1,1,0 \ right) & = {\ frac {\ sqrt {3}} {{\ sqrt {\ pi}} | x |}} \ exp \ left (- {\ tfrac {16} {27}} x ^ {- 2} \ right) W _ {{\ frac {1} {2}}, {\ frac {1} {6}}} \ left ({\ tfrac {32} {27}} x ^ {- 2} \ right) \\ [8pt] f \ left (x; {\ tfrac {3} {2}}, 1,1,0 \ right) & = {\ begin {cases} {\ frac {\ sqrt {3}} {{\ sqrt {\ pi}} | x |}} \ exp \ left ({\ frac {1} {27}} x ^ {3} \ right) W _ {{\ frac { 1} {2}}, {\ frac {1} {6}}} \ left (- {\ frac {2} {27}} x ^ {3} \ right) & x <0 \\ {} \\ { \ frac {\ sqrt {3}} {6 {\ sqrt {\ pi}} | x |}} \ exp \ left ({\ frac {1} {27}} x ^ {3} \ right) W _ {- {\ frac {1} {2}}, {\ frac {1} {6}}} \ left ({\ frac {2} {27}} x ^ {3} \ right) & x \ geq 0 \ end { casos}} \ end {alinhados}}}$

Veja também

• Voo Lévy
• Processo Lévy
• Outras distribuições de "lei de potência"
  • Distribuição de pareto
  • Distribuição Zeta
  • Distribuição Zipf
  • Distribuição Zipf-Mandelbrot
• Distribuições estáveis ​​e moderadas com agrupamento de volatilidade - aplicações financeiras
• Distribuição estável multivariada
• Distribuição discreta estável

Notas

• O programa STABLE para Windows está disponível na página da Web estável de John Nolan: http://www.robustanalysis.com/public/stable.html . Ele calcula a densidade (pdf), função de distribuição cumulativa (cdf) e quantis para uma distribuição geral estável e realiza estimativa de máxima verossimilhança de parâmetros estáveis ​​e algumas técnicas de análise exploratória de dados para avaliar o ajuste de um conjunto de dados.
• libstable é uma implementação C para a distribuição Stable pdf, cdf, número aleatório, quantil e funções de ajuste (junto com um pacote de replicação de benchmark e um pacote R).
• Pacote R 'stabledist' por Diethelm Wuertz, Martin Maechler e membros da equipe principal da Rmetrics. Calcula densidade, probabilidade, quantis e números aleatórios estáveis. Atualizado em 12 de setembro de 2016.

Referências