Lei dos grandes números - Law of large numbers

Uma ilustração da lei dos grandes números usando uma determinada série de jogadas de um único dado . À medida que o número de jogadas nesta execução aumenta, a média dos valores de todos os resultados se aproxima de 3,5. Embora cada corrida mostrasse uma forma distinta em um pequeno número de lances (à esquerda), em um grande número de jogadas (à direita) as formas seriam extremamente semelhantes.

Parte de uma série de estatísticas
Teoria da probabilidade
Probabilidade Axiomas Determinismo Sistema Indeterminismo Aleatoriedade
Espaço de probabilidade Espaço amostral Evento Eventos coletivamente exaustivos Evento elementar Exclusividade mútua Resultado Singleton Experimentar Julgamento de Bernoulli Distribuição de probabilidade Distribuição Bernoulli Distribuição binomial Distribuição normal Medida de probabilidade Variável aleatória Processo Bernoulli Contínuo ou discreto Valor esperado Cadeia de Markov Valor observado Caminhada aleatória Processo estocástico
Evento complementar Probabilidade conjunta Probabilidade marginal Probabilidade Condicional
Independência Independência condicional Lei da probabilidade total Lei dos grandes números Teorema de Bayes Desigualdade de Boole
Diagrama de Venn Diagrama de árvore
v t e

Na teoria da probabilidade , a lei dos grandes números ( LLN ) é um teorema que descreve o resultado de realizar o mesmo experimento um grande número de vezes. De acordo com a lei, a média dos resultados obtidos em um grande número de tentativas deve ser próxima ao valor esperado e tenderá a se aproximar do valor esperado à medida que mais tentativas são realizadas.

O LLN é importante porque garante resultados estáveis ​​de longo prazo para as médias de alguns eventos aleatórios. Por exemplo, embora um cassino possa perder dinheiro em um único giro da roleta , seus ganhos tenderão a uma porcentagem previsível em um grande número de giros. Qualquer seqüência de vitórias de um jogador acabará sendo superada pelos parâmetros do jogo. É importante ressaltar que a lei só se aplica (como o nome indica) quando um grande número de observações é considerado. Não existe um princípio de que um pequeno número de observações irá coincidir com o valor esperado ou que uma seqüência de um valor será imediatamente "equilibrada" pelos outros (veja a falácia do jogador ).

Exemplos

Por exemplo, um único lançamento de um dado justo de seis lados produz um dos números 1, 2, 3, 4, 5 ou 6, cada um com igual probabilidade . Portanto, o valor esperado da média dos rolos é:

${\ displaystyle {\ frac {1 + 2 + 3 + 4 + 5 + 6} {6}} = 3,5}$

De acordo com a lei dos grandes números, se um grande número de dados de seis lados for lançado, a média de seus valores (às vezes chamada de média amostral ) provavelmente será próxima a 3,5, com a precisão aumentando à medida que mais dados são lançados.

Segue-se da lei dos grandes números que a probabilidade empírica de sucesso em uma série de tentativas de Bernoulli convergirá para a probabilidade teórica. Para uma variável aleatória de Bernoulli , o valor esperado é a probabilidade teórica de sucesso, e a média de n tais variáveis ​​(assumindo que sejam independentes e distribuídas de forma idêntica (iid) ) é precisamente a frequência relativa.

Por exemplo, um cara ou coroa justo é um julgamento de Bernoulli. Quando uma moeda justa é jogada uma vez, a probabilidade teórica de que o resultado será cara é igual a 1 ⁄ 2 . Portanto, de acordo com a lei dos grandes números, a proporção de caras em um "grande" número de lançamentos de moeda "deve ser" aproximadamente 1 ⁄ 2 . Em particular, a proporção de caras após n flips irá quase certamente convergir para 1 ⁄ 2 conforme n se aproxima do infinito.

Embora a proporção de caras (e coroas) se aproxime de 1/2, quase certamente a diferença absoluta no número de caras e coroas se tornará grande à medida que o número de viradas se torna grande. Ou seja, a probabilidade de que a diferença absoluta seja um número pequeno se aproxima de zero à medida que o número de lançamentos torna-se grande. Além disso, quase certamente a proporção da diferença absoluta para o número de lançamentos se aproximará de zero. Intuitivamente, a diferença esperada cresce, mas a uma taxa mais lenta do que o número de lançamentos.

Outro bom exemplo do LLN é o método Monte Carlo . Esses métodos são uma ampla classe de algoritmos computacionais que dependem de amostragem aleatória repetida para obter resultados numéricos. Quanto maior o número de repetições, melhor tende a ser a aproximação. A razão pela qual esse método é importante é principalmente que, às vezes, é difícil ou impossível usar outras abordagens.

Limitação

A média dos resultados obtidos em um grande número de tentativas pode não convergir em alguns casos. Por exemplo, a média de n resultados obtidos da distribuição de Cauchy ou de algumas distribuições de Pareto (α <1) não convergirão conforme n se torna maior; o motivo são caudas pesadas . A distribuição de Cauchy e a distribuição de Pareto representam dois casos: a distribuição de Cauchy não tem uma expectativa, enquanto a expectativa da distribuição de Pareto (α <1) é infinita. Outro exemplo é onde os números aleatórios são iguais à tangente de um ângulo uniformemente distribuído entre −90 ° e + 90 °. A mediana é zero, mas o valor esperado não existe e, de fato, a média de n tais variáveis ​​têm a mesma distribuição de uma dessas variáveis. Ele não converge em probabilidade para zero (ou qualquer outro valor) conforme n vai para o infinito.

E se os julgamentos incorporam um viés de seleção, típico do comportamento econômico / racional humano, a Lei dos grandes números não ajuda a resolver o viés. Mesmo que o número de tentativas seja aumentado, o viés de seleção permanece.

História

A difusão é um exemplo da lei dos grandes números. Inicialmente, existem moléculas de soluto no lado esquerdo de uma barreira (linha magenta) e nenhuma à direita. A barreira é removida e o soluto se espalha para encher todo o recipiente.
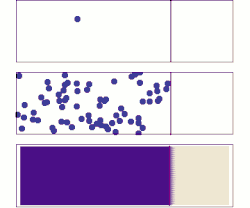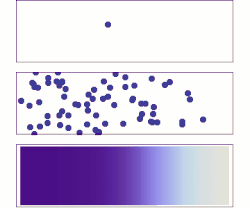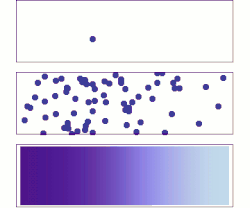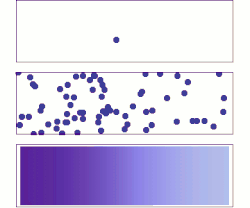
Acima: com uma única molécula, o movimento parece ser bastante aleatório.
Meio: Com mais moléculas, há claramente uma tendência em que o soluto preenche o recipiente mais e mais uniformemente, mas também há flutuações aleatórias.
Embaixo: Com um número enorme de moléculas de soluto (muitos para ver), a aleatoriedade praticamente se foi: o soluto parece mover-se suave e sistematicamente de áreas de alta concentração para áreas de baixa concentração. Em situações realistas, os químicos podem descrever a difusão como um fenômeno macroscópico determinístico (ver as leis de Fick ), apesar de sua natureza aleatória subjacente.

O matemático italiano Gerolamo Cardano (1501–1576) afirmou sem provas que a exatidão das estatísticas empíricas tendem a melhorar com o número de tentativas. Isso foi formalizado como uma lei dos grandes números. Uma forma especial do LLN (para uma variável aleatória binária) foi provada pela primeira vez por Jacob Bernoulli . Demorou mais de 20 anos para desenvolver uma prova matemática suficientemente rigorosa que foi publicada em seu Ars Conjectandi (A Arte de Conjecturar) em 1713. Ele chamou isso de seu "Teorema de Ouro", mas tornou-se geralmente conhecido como " Teorema de Bernoulli ". Isso não deve ser confundido com o princípio de Bernoulli , em homenagem ao sobrinho de Jacob Bernoulli, Daniel Bernoulli . Em 1837, SD Poisson a descreveu sob o nome de " la loi des grands nombres " ("a lei dos grandes números"). Posteriormente, era conhecido por ambos os nomes, mas a "lei dos grandes números" é usada com mais frequência.

Depois que Bernoulli e Poisson publicaram seus esforços, outros matemáticos também contribuíram para o refinamento da lei, incluindo Chebyshev , Markov , Borel , Cantelli e Kolmogorov e Khinchin . Markov mostrou que a lei pode ser aplicada a uma variável aleatória que não tem uma variância finita sob alguma outra suposição mais fraca, e Khinchin mostrou em 1929 que se a série consiste em variáveis ​​aleatórias independentes distribuídas de forma idêntica, é suficiente que o valor esperado exista para o lei fraca de grandes números para ser verdade. Esses estudos adicionais deram origem a duas formas proeminentes de LLN. Uma é chamada de lei "fraca" e a outra de lei "forte", em referência a dois modos diferentes de convergência das médias amostrais cumulativas para o valor esperado; em particular, conforme explicado abaixo, a forma forte implica na forma fraca.

Formulários

Existem duas versões diferentes da lei dos grandes números que são descritas abaixo. Elas são chamadas de lei forte dos grandes números e lei fraca dos grandes números . Declarado para o caso em que X ₁ , X ₂ , ... é uma sequência infinita de variáveis ​​aleatórias integráveis ​​de Lebesgue independentes e identicamente distribuídas (iid) com valor esperado E ( X ₁ ) = E ( X ₂ ) = ... = µ , ambas as versões da lei afirmam que - com certeza virtual - a média da amostra

${\ displaystyle {\ overline {X}} _ {n} = {\ frac {1} {n}} (X_ {1} + \ cdots + X_ {n})}$

converge para o valor esperado:

${\ displaystyle {\ overline {X}} _ {n} \ to \ mu \ quad {\ textrm {as}} \ n \ to \ infty.}$

( lei. 1 )

(A integrabilidade de Lebesgue de X _j significa que o valor esperado E ( X _j ) existe de acordo com a integração de Lebesgue e é finito. Isso não significa que a medida de probabilidade associada é absolutamente contínua em relação à medida de Lebesgue .)

Com base na (desnecessária, veja abaixo) suposição de variância finita (para todos ) e nenhuma correlação entre variáveis ​​aleatórias, a variância da média de n variáveis ​​aleatórias ${\ displaystyle \ operatorname {Var} (X_ {i}) = \ sigma ^ {2}}$${\ displaystyle i}$

${\ displaystyle \ operatorname {Var} ({\ overline {X}} _ {n}) = \ operatorname {Var} ({\ tfrac {1} {n}} (X_ {1} + \ cdots + X_ {n })) = {\ frac {1} {n ^ {2}}} \ operatorname {Var} (X_ {1} + \ cdots + X_ {n}) = {\ frac {n \ sigma ^ {2}} {n ^ {2}}} = {\ frac {\ sigma ^ {2}} {n}}.}$

Observe que esta suposição de variância finita não é necessária . A variância grande ou infinita tornará a convergência mais lenta, mas o LLN se mantém de qualquer maneira. Essa suposição é freqüentemente usada porque torna as provas mais fáceis e mais curtas. ${\ displaystyle \ operatorname {Var} (X_ {1}) = \ operatorname {Var} (X_ {2}) = \ ldots = \ sigma ^ {2} <\ infty}$

A independência mútua das variáveis ​​aleatórias pode ser substituída pela independência dos pares em ambas as versões da lei.

A diferença entre a versão forte e a fraca está relacionada ao modo de convergência que está sendo afirmado. Para a interpretação desses modos, consulte Convergência de variáveis ​​aleatórias .

Lei fraca

Simulação ilustrando a lei dos grandes números. Cada moldura, uma moeda que é vermelha de um lado e azul do outro, é lançada e um ponto é adicionado na coluna correspondente. Um gráfico de pizza mostra a proporção de vermelho e azul até agora. Observe que, embora a proporção varie significativamente no início, ela se aproxima de 50% à medida que o número de tentativas aumenta.

A lei fraca dos grandes números (também chamada de lei de Khinchin ) afirma que a média da amostra converge em probabilidade para o valor esperado

${\ displaystyle {\ begin {matrix} {} \\ {\ overline {X}} _ {n} \ {\ xrightarrow {P}} \ \ mu \ qquad {\ textrm {quando}} \ n \ to \ infty . \\ {} \ end {matriz}}}$

( lei. 2 )

Ou seja, para qualquer número positivo ε ,

${\ displaystyle \ lim _ {n \ to \ infty} \ Pr \! \ left (\, | {\ overline {X}} _ {n} - \ mu |> \ varepsilon \, \ right) = 0.}$

Interpretando esse resultado, a lei fraca afirma que para qualquer margem diferente de zero especificada ( ε ), não importa quão pequena, com uma amostra grande o suficiente, haverá uma probabilidade muito alta de que a média das observações estará próxima do valor esperado; ou seja, dentro da margem.

Conforme mencionado anteriormente, a lei fraca se aplica no caso de variáveis ​​aleatórias iid, mas também se aplica em alguns outros casos. Por exemplo, a variância pode ser diferente para cada variável aleatória da série, mantendo o valor esperado constante. Se as variâncias são limitadas, então a lei se aplica, como mostrado por Chebyshev já em 1867. (Se os valores esperados mudam durante a série, então podemos simplesmente aplicar a lei ao desvio médio dos respectivos valores esperados. A lei então afirma que isso converge em probabilidade para zero.) De fato, a prova de Chebyshev funciona desde que a variância da média dos primeiros n valores vá para zero enquanto n vai para o infinito. Como exemplo, suponha que cada variável aleatória na série segue uma distribuição gaussiana com média zero, mas com variância igual a , que não é limitada. Em cada estágio, a média será normalmente distribuída (como a média de um conjunto de variáveis ​​normalmente distribuídas). A variância da soma é igual à soma das variâncias, que é assintótica a . A variância da média é, portanto, assintótica e vai para zero. ${\ displaystyle 2n / \ log (n + 1)}$${\ displaystyle n ^ {2} / \ log n}$${\ displaystyle 1 / \ log n}$

Existem também exemplos de aplicação da lei fraca, embora o valor esperado não exista.

Lei forte

A lei forte dos grandes números (também chamada de lei de Kolmogorov ) afirma que a média da amostra converge quase que certamente para o valor esperado

${\ displaystyle {\ begin {matrix} {} \\ {\ overline {X}} _ {n} \ \ xrightarrow {\ text {as}} \ \ mu \ qquad {\ textrm {quando}} \ n \ para \ infty. \\ {} \ end {matriz}}}$

( lei. 3 )

Isso é,

${\ displaystyle \ Pr \! \ left (\ lim _ {n \ to \ infty} {\ overline {X}} _ {n} = \ mu \ right) = 1.}$

O que isso significa é que a probabilidade de que, à medida que o número de tentativas n vai ao infinito, a média das observações converge para o valor esperado, é igual a um.

A prova é mais complexa do que a da lei fraca. Esta lei justifica a interpretação intuitiva do valor esperado (apenas para integração de Lebesgue) de uma variável aleatória quando amostrada repetidamente como a "média de longo prazo".

A convergência quase certa também é chamada de convergência forte de variáveis ​​aleatórias. Essa versão é chamada de lei forte porque as variáveis ​​aleatórias que convergem fortemente (quase com certeza) têm garantia de convergência fraca (em probabilidade). No entanto, sabe-se que a lei fraca é válida em certas condições onde a lei forte não é válida e então a convergência é apenas fraca (em probabilidade). Veja # Diferenças entre a lei fraca e a lei forte .

A própria lei forte dos grandes números pode ser vista como um caso especial do teorema ergódico pontual .

A lei forte se aplica a variáveis ​​aleatórias independentes distribuídas de forma idêntica com um valor esperado (como a lei fraca). Isso foi provado por Kolmogorov em 1930. Também pode ser aplicado em outros casos. Kolmogorov também mostrou, em 1933, que se as variáveis ​​são independentes e distribuídas de forma idêntica, então para a média convergir quase certamente para algo (isso pode ser considerado outra afirmação da lei forte), é necessário que tenham um valor esperado ( e então, é claro, a média convergirá quase com certeza sobre isso).

Se as somas forem independentes, mas não distribuídas de forma idêntica, então

${\ displaystyle {\ overline {X}} _ {n} - \ operatorname {E} {\ big [} {\ overline {X}} _ {n} {\ big]} \ {\ xrightarrow {\ text {as }}} \ 0,}$

desde que cada X _k tenha um segundo momento finito e

${\ displaystyle \ sum _ {k = 1} ^ {\ infty} {\ frac {1} {k ^ {2}}} \ operatorname {Var} [X_ {k}] <\ infty.}$

Esta afirmação é conhecida como lei forte de Kolmogorov , ver, por exemplo, Sen & Singer (1993 , Teorema 2.3.10).

Um exemplo de série onde a lei fraca se aplica, mas não a lei forte, é quando X _k é mais ou menos (começando em k suficientemente grande para que o denominador seja positivo) com probabilidade 1/2 para cada. A variância de X _k é então a lei forte de Kolmogorov não se aplica porque a soma parcial em seu critério até k = n é assintótica a e isso é ilimitado. ${\ displaystyle {\ sqrt {k / \ log \ log \ log k}}}$${\ displaystyle k / \ log \ log \ log k.}$${\ displaystyle \ log n / \ log \ log \ log n}$

Se substituirmos as variáveis ​​aleatórias por variáveis ​​gaussianas com as mesmas variâncias, a saber , a média em qualquer ponto também será normalmente distribuída. A largura da distribuição da média tenderá para zero (desvio padrão assintótico para ), mas para um dado ε, há probabilidade que não vai a zero com n, enquanto a média algum tempo após a n- ésima tentativa voltará a subir para ε. Como a largura da distribuição da média não é zero, ela deve ter um limite inferior positivo p (ε), o que significa que há uma probabilidade de pelo menos p (ε) de que a média irá atingir ε após n tentativas. Isso acontecerá com probabilidade p (ε) / 2 antes de algum m que depende de n . Mas mesmo depois de m , ainda há uma probabilidade de pelo menos p (ε) de que isso aconteça. (Isso parece indicar que p (ε) = 1 e a média atingirá ε um número infinito de vezes.) ${\ displaystyle {\ sqrt {k / \ log \ log \ log k}},}$${\ displaystyle 1 / {\ sqrt {2 \ log \ log \ log n}}}$

Diferenças entre a lei fraca e a lei forte

A lei fraca afirma que, para um n grande especificado , a média provavelmente será próxima de μ . Assim, deixa em aberto a possibilidade de que aconteça um número infinito de vezes, embora em intervalos infrequentes. (Não necessariamente para todos os n). ${\ displaystyle {\ overline {X}} _ {n}}$${\ displaystyle | {\ overline {X}} _ {n} - \ mu |> \ varepsilon}$${\ displaystyle | {\ overline {X}} _ {n} - \ mu | \ neq 0}$

A lei forte mostra que isso quase certamente não ocorrerá. Em particular, isso implica que, com probabilidade 1, temos que para qualquer ε > 0 a desigualdade é válida para todos os n grandes o suficiente . ${\ displaystyle | {\ overline {X}} _ {n} - \ mu | <\ varepsilon}$

A lei forte não vale nos seguintes casos, mas a lei fraca sim.

1. Seja X uma variável aleatória distribuída exponencialmente com o parâmetro 1. A variável aleatória não tem valor esperado de acordo com a integração de Lebesgue, mas usando a convergência condicional e interpretando a integral como uma integral de Dirichlet , que é uma integral de Riemann imprópria , podemos dizer: ${\ displaystyle \ sin (X) e ^ {X} X ^ {- 1}}$

${\ displaystyle E \ left ({\ frac {\ sin (X) e ^ {X}} {X}} \ right) = \ \ int _ {0} ^ {\ infty} {\ frac {\ sin (x ) e ^ {x}} {x}} e ^ {- x} dx = {\ frac {\ pi} {2}}}$

2. Seja x uma distribuição geométrica com probabilidade 0,5. A variável aleatória não tem um valor esperado no sentido convencional porque a série infinita não é absolutamente convergente, mas usando a convergência condicional, podemos dizer: ${\ displaystyle 2 ^ {X} (- 1) ^ {X} X ^ {- 1}}$

${\ displaystyle E \ left ({\ frac {2 ^ {X} (- 1) ^ {X}} {X}} \ right) = \ \ sum _ {1} ^ {\ infty} {\ frac {2 ^ {x} (- 1) ^ {x}} {x}} 2 ^ {- x} = - \ ln (2)}$

3. Se a função de distribuição cumulativa de uma variável aleatória é

${\ displaystyle 1-F (x) = {\ frac {e} {2x \ ln (x)}}, x \ geq e}$

${\ displaystyle F (x) = {\ frac {e} {- 2x \ ln (-x)}}, x \ leq -e}$

então não tem valor esperado, mas a lei fraca é verdadeira.

Lei uniforme de grandes números

Suponha que f ( x , θ ) seja alguma função definida para θ ∈ Θ e contínua em θ . Então, para qualquer θ fixo , a sequência { f ( X ₁ , θ ), f ( X ₂ , θ ), ...} será uma sequência de variáveis ​​aleatórias independentes e distribuídas de forma idêntica, de modo que a média da amostra desta sequência converge em probabilidade para E [ f ( X , θ )]. Esta é a convergência pontual (em θ ).

A lei uniforme dos grandes números estabelece as condições sob as quais a convergência ocorre uniformemente em θ . Se

1. Θ é compacto,
2. f ( x , θ ) é contínuo em cada θ ∈ Θ para quase todos os x s, e função mensurável de x em cada θ .
3. existe uma função dominante d ( x ) tal que E [ d ( X )] <∞, e

   ${\ displaystyle \ left \ | f (x, \ theta) \ right \ | \ leq d (x) \ quad {\ text {para todos}} \ \ theta \ in \ Theta.}$

Então E [ f ( X , θ )] é contínuo em θ , e

${\ displaystyle \ sup _ {\ theta \ in \ Theta} \ left \ | {\ frac {1} {n}} \ sum _ {i = 1} ^ {n} f (X_ {i}, \ theta) - \ operatorname {E} [f (X, \ theta)] \ right \ | {\ xrightarrow {\ mathrm {as}}} \ 0.}$

Esse resultado é útil para derivar a consistência de uma grande classe de estimadores (consulte Estimador Extremum ).

Lei de Borel dos grandes números

A lei dos grandes números de Borel , nomeada em homenagem a Émile Borel , afirma que se um experimento é repetido um grande número de vezes, independentemente sob condições idênticas, então a proporção de vezes que qualquer evento especificado ocorre aproximadamente igual à probabilidade de ocorrência do evento em qualquer tentativas; quanto maior o número de repetições, melhor tende a ser a aproximação. Mais precisamente, se E denota o evento em questão, p sua probabilidade de ocorrência, e N _n ( E ) o número de vezes que E ocorre nas primeiras n tentativas, então com probabilidade um,

${\ displaystyle {\ frac {N_ {n} (E)} {n}} \ to p {\ text {as}} n \ to \ infty.}$

Este teorema torna rigorosa a noção intuitiva de probabilidade como a frequência relativa de longo prazo da ocorrência de um evento. É um caso especial de qualquer uma das várias leis mais gerais de grandes números na teoria da probabilidade.

Desigualdade de Chebyshev . Seja X uma variável aleatória com valor esperado finito μ e variância não nula finita σ ² . Então, para qualquer número real k > 0 ,

${\ displaystyle \ Pr (| X- \ mu | \ geq k \ sigma) \ leq {\ frac {1} {k ^ {2}}}.}$

Prova da lei fraca

Dado X ₁ , X ₂ , ... uma sequência infinita de variáveis aleatórias iid com valor finito esperado E ( X ₁ ) = E ( X ₂ ) = ... = µ <∞, estamos interessados ​​na convergência da amostra média

${\ displaystyle {\ overline {X}} _ {n} = {\ tfrac {1} {n}} (X_ {1} + \ cdots + X_ {n}).}$

A fraca lei dos grandes números afirma:

Teorema: ${\ displaystyle {\ begin {matrix} {} \\ {\ overline {X}} _ {n} \ {\ xrightarrow {P}} \ \ mu \ qquad {\ textrm {quando}} \ n \ to \ infty . \\ {} \ end {matriz}}}$

( lei. 2 )

Prova usando a desigualdade de Chebyshev assumindo variância finita

Esta prova usa a suposição de variância finita (para todos ). A independência das variáveis ​​aleatórias implica nenhuma correlação entre elas, e temos que ${\ displaystyle \ operatorname {Var} (X_ {i}) = \ sigma ^ {2}}$${\ displaystyle i}$

${\ displaystyle \ operatorname {Var} ({\ overline {X}} _ {n}) = \ operatorname {Var} ({\ tfrac {1} {n}} (X_ {1} + \ cdots + X_ {n })) = {\ frac {1} {n ^ {2}}} \ operatorname {Var} (X_ {1} + \ cdots + X_ {n}) = {\ frac {n \ sigma ^ {2}} {n ^ {2}}} = {\ frac {\ sigma ^ {2}} {n}}.}$

A média comum μ da sequência é a média da média da amostra:

${\ displaystyle E ({\ overline {X}} _ {n}) = \ mu.}$

Usando a desigualdade de Chebyshev nos resultados em ${\ displaystyle {\ overline {X}} _ {n}}$

${\ displaystyle \ operatorname {P} (\ left | {\ overline {X}} _ {n} - \ mu \ right | \ geq \ varepsilon) \ leq {\ frac {\ sigma ^ {2}} {n \ varejpsilon ^ {2}}}.}$

Isso pode ser usado para obter o seguinte:

${\ displaystyle \ operatorname {P} (\ left | {\ overline {X}} _ {n} - \ mu \ right | <\ varepsilon) = 1- \ operatorname {P} (\ left | {\ overline {X }} _ {n} - \ mu \ right | \ geq \ varepsilon) \ geq 1 - {\ frac {\ sigma ^ {2}} {n \ varepsilon ^ {2}}}.}$

Conforme n se aproxima do infinito, a expressão se aproxima de 1. E por definição de convergência em probabilidade , obtivemos

${\ displaystyle {\ begin {matrix} {} \\ {\ overline {X}} _ {n} \ {\ xrightarrow {P}} \ \ mu \ qquad {\ textrm {quando}} \ n \ to \ infty . \\ {} \ end {matriz}}}$

( lei. 2 )

Prova usando convergência de funções características

Pelo teorema de Taylor para funções complexas , a função característica de qualquer variável aleatória, X , com média finita μ, pode ser escrita como

${\ displaystyle \ varphi _ {X} (t) = 1 + it \ mu + o (t), \ quad t \ rightarrow 0.}$

Todos os X ₁ , X ₂ , ... têm a mesma função característica, por isso vamos simplesmente denotar este φ _X .

Entre as propriedades básicas das funções características, existem

${\ displaystyle \ varphi _ {{\ frac {1} {n}} X} (t) = \ varphi _ {X} ({\ tfrac {t} {n}}) \ quad {\ text {e}} \ quad \ varphi _ {X + Y} (t) = \ varphi _ {X} (t) \ varphi _ {Y} (t) \ quad}$se X e Y são independentes.

Essas regras podem ser usadas para calcular a função característica de em termos de φ _X : ${\ displaystyle \ scriptstyle {\ overline {X}} _ {n}}$

${\ displaystyle \ varphi _ {{\ overline {X}} _ {n}} (t) = \ left [\ varphi _ {X} \ left ({t \ over n} \ right) \ right] ^ {n } = \ left [1 + i \ mu {t \ over n} + o \ left ({t \ over n} \ right) \ right] ^ {n} \, \ rightarrow \, e ^ {it \ mu} , \ quad {\ text {as}} \ quad n \ rightarrow \ infty.}$

O limite   e ^{it μ}   é a função característica da variável aleatória constante μ e, portanto, pelo teorema da continuidade de Lévy , converge na distribuição para μ: ${\ displaystyle \ scriptstyle {\ overline {X}} _ {n}}$

${\ displaystyle {\ overline {X}} _ {n} \, {\ xrightarrow {\ mathcal {D}}} \, \ mu \ qquad {\ text {for}} \ qquad n \ to \ infty.}$

μ é uma constante, o que implica que a convergência na distribuição para μ e a convergência na probabilidade para μ são equivalentes (consulte Convergência de variáveis ​​aleatórias .) Portanto,

${\ displaystyle {\ begin {matrix} {} \\ {\ overline {X}} _ {n} \ {\ xrightarrow {P}} \ \ mu \ qquad {\ textrm {quando}} \ n \ to \ infty . \\ {} \ end {matriz}}}$

( lei. 2 )

Isso mostra que a média da amostra converge em probabilidade para a derivada da função característica na origem, desde que esta exista.

Consequências

A lei dos grandes números fornece uma expectativa de uma distribuição desconhecida de uma realização da sequência, mas também qualquer característica da distribuição de probabilidade. Aplicando a lei de Borel dos grandes números , pode-se facilmente obter a função de massa de probabilidade. Para cada evento na função de massa de probabilidade objetiva, pode-se aproximar a probabilidade de ocorrência do evento com a proporção de vezes que qualquer evento especificado ocorre. Quanto maior o número de repetições, melhor será a aproximação. Quanto ao caso contínuo:, para h positivo pequeno. Assim, para n grande: ${\ displaystyle C = (ah, a + h]}$

$${\ displaystyle {\ frac {N_ {n} (C)} {n}} \ thickapprox p = P (X \ in C) = \ int _ {ah} ^ {a + h} f (x) dx \ thickapprox 2hf (a)}$$

Com este método, pode-se cobrir todo o eixo x com uma grade (com tamanho de grade 2h) e obter um gráfico de barras que é chamado de histograma .

Veja também

• Propriedade de equipartição assintótica
• Teorema do limite central
• Teorema do macaco infinito
• Lei das médias
• Lei do logaritmo iterado
• Lei dos números verdadeiramente grandes
• Efeito Lindy
• Regressão em direção à média
• Sorteio

Notas

Referências

links externos

• "Law of large numbers" , Encyclopedia of Mathematics , EMS Press , 2001 [1994]
• Weisstein, Eric W. "Weak Law of Large Numbers" . MathWorld .
• Weisstein, Eric W. "Strong Law of Large Numbers" . MathWorld .
• Animações para a Lei dos Grandes Números de Yihui Xie usando a animação do pacote R
• O CEO da Apple, Tim Cook, disse algo que faria os estatísticos estremecerem . "Não acreditamos em leis como leis de grande número. Isso é uma espécie de, uh, velho dogma, eu acho, que foi inventado por alguém [..]" disse Tim Cook e ao mesmo tempo: "No entanto, a lei de grandes números não tem nada a ver com grandes empresas, grandes receitas ou grandes taxas de crescimento. A lei dos grandes números é um conceito fundamental na teoria da probabilidade e estatística, associando as probabilidades teóricas que podemos calcular aos resultados reais dos experimentos que nós desempenho empírico. explicou o Business Insider