Decomposição da árvore - Tree decomposition

Um gráfico com oito vértices e uma decomposição em árvore dele em uma árvore com seis nós. Cada aresta do gráfico conecta dois vértices que são listados juntos em algum nó da árvore, e cada vértice do gráfico é listado nos nós de uma subárvore contígua da árvore. Cada nó da árvore lista no máximo três vértices, então a largura dessa decomposição é dois.

Na teoria dos grafos , uma decomposição em árvore é um mapeamento de um gráfico em uma árvore que pode ser usada para definir a largura da árvore do gráfico e acelerar a resolução de certos problemas computacionais no gráfico.

As decomposições de árvores também são chamadas de árvores de junção , árvores de clique ou árvores de junção ; eles desempenham um papel importante em problemas como inferência probabilística , satisfação de restrição , otimização de consulta e decomposição de matriz .

O conceito de decomposição de árvores foi originalmente introduzido por Rudolf Halin  ( 1976 ). Mais tarde, foi redescoberto por Neil Robertson e Paul Seymour  ( 1984 ) e desde então foi estudado por muitos outros autores.

Definição

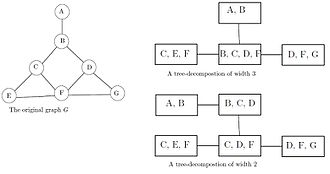
Intuitivamente, uma decomposição em árvore representa os vértices de um dado grafo G como subárvores de uma árvore, de modo que os vértices no grafo dado são adjacentes apenas quando as subárvores correspondentes se cruzam. Assim, G forma um subgráfico do gráfico de interseção das subárvores. O gráfico de interseção completo é um gráfico de cordas .

Cada subárvore associa um vértice do gráfico a um conjunto de nós da árvore. Para definir isso formalmente, representamos cada nó da árvore como o conjunto de vértices associados a ele. Assim, dado um gráfico G = ( V , E ), uma decomposição em árvore é um par ( X , T ), onde X = { X ₁ , ..., X _n } é uma família de subconjuntos (às vezes chamados de sacos ) de V e T é uma árvore cujos nós são os subconjuntos X _i , satisfazendo as seguintes propriedades:

1. A união de todos os conjuntos X _i é igual a V . Ou seja, cada vértice do gráfico está associado a pelo menos um nó da árvore.
2. Para cada aresta ( v , w ) no gráfico, há um subconjunto X _i que contém v e w . Ou seja, os vértices são adjacentes no gráfico apenas quando as subárvores correspondentes têm um nó em comum.
3. Se X _i e X _j contêm um vértice v , então todos os nós X _k da árvore no caminho (único) entre X _i e X _j contêm v também. Isto é, os nós associados com vértice v formar um subconjunto ligado de T . Isso também é conhecido como coerência ou propriedade de interseção em execução . Pode-se afirmar de forma equivalente que se , e são nós, e está no caminho de para , então .${\ displaystyle X_ {i}}$${\ displaystyle X_ {j}}$${\ displaystyle X_ {k}}$${\ displaystyle X_ {k}}$${\ displaystyle X_ {i}}$${\ displaystyle X_ {j}}$${\ displaystyle X_ {i} \ cap X_ {j} \ subseteq X_ {k}}$

A decomposição em árvore de um gráfico está longe de ser única; por exemplo, uma decomposição de árvore trivial contém todos os vértices do gráfico em seu único nó raiz.

Uma decomposição de árvore na qual a árvore subjacente é um gráfico de caminho é chamada de decomposição de caminho, e o parâmetro de largura derivado desses tipos especiais de decomposição de árvore é conhecido como largura de caminho .

Uma decomposição em árvore ( X , T = ( I , F )) de largura de árvore k é suave , se para todos e para todos . ${\ displaystyle i \ in I: | X_ {i} | = k + 1}$${\ displaystyle (i, j) \ in F: | X_ {i} \ cap X_ {j} | = k}$

O número mínimo de árvores em uma decomposição de árvore é o número da árvore de G.

Largura da árvore

Duas decomposições em árvore diferentes do mesmo gráfico

A largura da decomposição de uma árvore é o tamanho de seu maior conjunto X _i menos um. O treewidth tw ( L ) de um gráfico que L é a largura mínima entre todas as decomposições árvore possíveis de L . Nesta definição, o tamanho do maior conjunto é diminuído em um para tornar a largura da árvore de uma árvore igual a um. A largura da árvore também pode ser definida a partir de outras estruturas além das decomposições de árvore, incluindo gráficos de cordas , silvas e refúgios .

É NP-completo determinar se um dado gráfico G tem largura de árvore no máximo uma dada variável k . No entanto, quando k é qualquer constante fixa, os gráficos com largura de árvore k podem ser reconhecidos, e uma decomposição de árvore de largura k construída para eles, em tempo linear. A dependência do tempo desse algoritmo em k é exponencial.

Programaçao dinamica

No início da década de 1970, observou-se que uma grande classe de problemas de otimização combinatória definidos em grafos podiam ser eficientemente resolvidos por programação dinâmica não serial , desde que o gráfico tivesse uma dimensão limitada , um parâmetro relacionado à largura da árvore. Posteriormente, vários autores observaram independentemente, no final da década de 1980, que muitos problemas algorítmicos que são NP-completos para grafos arbitrários podem ser resolvidos de forma eficiente por programação dinâmica para grafos de largura de árvore limitada, usando as decomposições em árvore desses grafos.

Como exemplo, considere o problema de encontrar o conjunto independente máximo em um gráfico de largura de árvore k . Para resolver este problema, primeiro escolha um dos nós da decomposição da árvore para ser a raiz, arbitrariamente. Para um nó X _i da decomposição da árvore, seja D _i a união dos conjuntos X _j descendentes de X _i . Para um conjunto independente S  ⊂  X _i , deixe uma ( S , i ) denotam o tamanho do maior subconjunto independente I de D _i tal que I  ∩  X _i  =  S . Da mesma forma, para um par adjacente de nós X _i e X _j , com X _i mais longe da raiz da árvore do que X _j , e um conjunto independente S  ⊂  X _i  ∩  X _j , seja B ( S , i , j ) denotando o tamanho do maior subconjunto independente I de D _i tal que I  ∩  X _i  ∩  X _j  =  S . Podemos calcular esses valores A e B por meio de uma travessia ascendente da árvore:

${\ displaystyle A (S, i) = | S | + \ sum _ {j} \ left (B (S \ cap X_ {j}, j, i) - | S \ cap X_ {j} | \ right) }$

${\ displaystyle B (S, i, j) = \ max _ {S '\ subconjunto X_ {i} \ atop S = S' \ cap X_ {j}} A (S ', i)}$

onde a soma no cálculo de está sobre os filhos de nó . ${\ displaystyle A (S, i)}$${\ displaystyle X_ {i}}$

Em cada nó ou aresta, existem no máximo 2 ^k conjuntos S para os quais precisamos calcular esses valores, portanto, se k for uma constante, todo o cálculo leva um tempo constante por aresta ou nó. O tamanho do conjunto independente máximo é o maior valor armazenado no nó raiz, e o próprio conjunto independente máximo pode ser encontrado (como é padrão em algoritmos de programação dinâmica) retrocedendo por meio desses valores armazenados a partir desse maior valor. Assim, em gráficos de largura de árvore limitada, o problema do conjunto independente máximo pode ser resolvido em tempo linear. Algoritmos semelhantes se aplicam a muitos outros problemas de grafos.

Esta abordagem de programação dinâmica é usada no aprendizado de máquina por meio do algoritmo de árvore de junção para propagação de crenças em gráficos de largura de árvore limitada. Ele também desempenha um papel fundamental em algoritmos para calcular a largura da árvore e construir decomposições de árvore: normalmente, esses algoritmos têm uma primeira etapa que se aproxima da largura da árvore, construindo uma decomposição em árvore com essa largura aproximada e, em seguida, uma segunda etapa que executa a programação dinâmica no decomposição aproximada da árvore para calcular o valor exato da largura da árvore.

Veja também

• Amoreiras e refúgios  - Dois tipos de estruturas que podem ser usadas como alternativa à decomposição em árvore na definição da largura da árvore de um gráfico.
• Decomposição de ramos  - Uma estrutura intimamente relacionada cuja largura está dentro de um fator constante de largura da árvore.
• Método de Decomposição  - Árvore de Decomposição é usado no Método de Decomposição para resolver o problema de satisfação de restrições.

Notas

Referências