Equação de Van der Waals - Van der Waals equation

Em química e termodinâmica , a equação de Van der Waals (ou equação de estado de Van der Waals ; em homenagem ao físico holandês Johannes Diderik van der Waals ) é uma equação de estado que generaliza a lei dos gases ideais com base em razões plausíveis de que gases reais não agem idealmente . A lei dos gases ideais trata as moléculas de gás como partículas pontuais que interagem com seus recipientes, mas não entre si, o que significa que elas não ocupam espaço nem alteram a energia cinética durante as colisões (ou seja, todas as colisões são perfeitamente elásticas ). A lei dos gases ideais afirma que o volume ( V ) ocupado por n moles de qualquer gás tem uma pressão ( P ) na temperatura ( T ) em kelvins dada pela seguinte relação, onde R é a constante do gás :

${\ displaystyle PV = nRT}$

Para contabilizar o volume que uma molécula de gás real ocupa, a equação de Van der Waals substitui V na lei dos gases ideais por , onde V _m é o volume molar do gás eb é o volume que é ocupado por um mol do moléculas. Isto leva a: ${\ displaystyle (V_ {m} -b)}$

${\ displaystyle P (V_ {m} -b) = RT}$

Equação de Van der Waals em uma parede em Leiden

A segunda modificação feita na lei dos gases ideais explica o fato de que as moléculas de gás de fato interagem umas com as outras (geralmente experimentam atração em baixas pressões e repulsão em altas pressões) e que gases reais, portanto, apresentam compressibilidade diferente dos gases ideais. Van der Waals providenciou a interação intermolecular adicionando à pressão observada P na equação de estado um termo , onde a é uma constante cujo valor depende do gás. A equação de Van der Waals é, portanto, escrita como: ${\ displaystyle a / V_ {m} ^ {2}}$

${\ displaystyle \ left (P + a {\ frac {1} {V_ {m} ^ {2}}} \ right) (V_ {m} -b) = RT}$

e, para n moles de gás, também pode ser escrito como a equação abaixo:

${\ displaystyle \ left (P + a {\ frac {n ^ {2}} {V ^ {2}}} \ right) (V-nb) = nRT}$

onde V _m é o volume molar do gás, R é a constante universal do gás, T é a temperatura, P é a pressão e V é o volume. Quando o volume molar V _m é grande, b torna-se desprezível em comparação com V _m , a / V _m ² torna-se desprezível em relação a P e a equação de Van der Waals se reduz à lei dos gases ideais, PV _m = RT .

Ele está disponível por meio de sua derivação tradicional (uma equação de estado mecânica) ou por meio de uma derivação baseada em termodinâmica estatística , a última das quais fornece a função de partição do sistema e permite que funções termodinâmicas sejam especificadas. Ele se aproxima com sucesso do comportamento de fluidos reais acima de suas temperaturas críticas e é qualitativamente razoável para seus estados líquido e gasoso de baixa pressão em baixas temperaturas. No entanto, perto das transições de fase entre gás e líquido, na faixa de p , V e T, onde a fase líquida e a fase gasosa estão em equilíbrio , a equação de Van der Waals falha em modelar com precisão o comportamento experimental observado, em particular que p é uma função constante de V em determinadas temperaturas. Como tal, o modelo de Van der Waals não é útil apenas para cálculos destinados a prever o comportamento real em regiões próximas do ponto crítico . Correções para lidar com essas deficiências preditivas já foram feitas, como a regra de área igual ou o princípio dos estados correspondentes .

Visão geral e história

A equação de Van der Waals é uma equação de estado termodinâmica baseada na teoria de que os fluidos são compostos de partículas com volumes diferentes de zero e sujeitos a uma força de atração interpartícula (não necessariamente em pares) . Foi baseado em um trabalho de físico-química teórica realizado no final do século 19 por Johannes Diderik van der Waals , que relatou um trabalho sobre a força atrativa que também leva seu nome. A equação é conhecida por ser baseada em um conjunto tradicional de derivações derivadas dos esforços de Van der Waals e relacionados, bem como um conjunto de derivações baseado em termodinâmica estatística , veja abaixo.

Os primeiros interesses de Van der Waals foram principalmente no campo da termodinâmica , onde uma primeira influência foi o trabalho publicado de Rudolf Clausius sobre o calor em 1857; outras influências significativas foram os escritos de James Clerk Maxwell , Ludwig Boltzmann e Willard Gibbs . Após a busca inicial de credenciais de ensino, o curso de graduação de Van der Waals em matemática e física na Universidade de Leiden, na Holanda, levou (com obstáculos significativos) à sua aceitação para estudos de doutorado em Leiden sob Pieter Rijke . Enquanto sua dissertação ajuda a explicar a observação experimental em 1869 pelo professor irlandês de química Thomas Andrews ( Queen's University Belfast ) sobre a existência de um ponto crítico nos fluidos, o historiador da ciência Martin J. Klein afirma que não está claro se Van der Waals foi ciente dos resultados de Andrews quando ele começou seu trabalho de doutorado. A pesquisa de doutorado de Van der Waals culminou em uma dissertação de 1873 que forneceu uma teoria semiquantitativa que descreve a mudança de estado gás-líquido e a origem de uma temperatura crítica, Over de Continuïteit van den Gas-en Vloeistof [-] toestand (holandês; em inglês, On the Continuity of the Gas- and Liquid-State ); foi nesta dissertação que surgiram as primeiras derivações do que hoje chamamos de equação de Van der Waals . James Clerk Maxwell revisou e elogiou seu conteúdo publicado na revista científica britânica Nature , e Van der Waals começou um trabalho independente que resultaria no recebimento do Prêmio Nobel em 1910, que enfatizou a contribuição de sua formulação desta "equação de estado para gases e líquidos. "

Equação

Isotermas de Van der Waals. O modelo prevê corretamente uma fase líquida principalmente incompressível, mas as oscilações na zona de transição de fase não se ajustam aos dados experimentais.

Van der Waals das isotérmicas e oscilações, temperaturas, T , abaixo e acima de T _C . Mostrado neste diagrama PV é uma série de 5 isotérmicas para temperaturas que variam de abaixo (azul) a acima (vermelho) T _C (a temperatura crítica), onde o aumento surge e o mergulho para baixo na isoterma prevista pela equação de Van der Waals ( a "oscilação", especialmente evidente para as duas isotermas para valores de T < T _C ), é evidente na região da transição de fase gás-líquido.

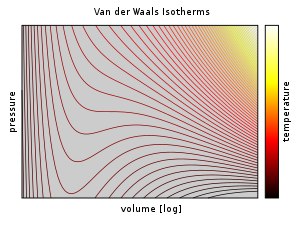
A equação refere-se quatro variáveis de estado: a pressão do fluido de p , o volume total do recipiente do fluido de V , o número de partículas N , e a temperatura absoluta do sistema T .

A forma intensiva e microscópica da equação é:

${\ displaystyle \ left (p + {\ frac {a '} {v ^ {2}}} \ right) \ left (v-b' \ right) = k _ {\ text {B}} T}$

Onde

${\ displaystyle v = V / N}$

é o volume do recipiente ocupado por cada partícula (não a velocidade de uma partícula), e k _B é a constante de Boltzmann . Ele introduz dois novos parâmetros: a ′, uma medida da atração média entre as partículas, eb ′, o volume excluído de v por uma partícula.

A equação também pode ser escrita em forma extensa e molar:

${\ displaystyle \ left (p + {\ frac {n ^ {2} a} {V ^ {2}}} \ right) \ left (V-nb \ right) = nRT}$

Onde

${\ displaystyle a = N_ {A} ^ {2} a '}$

é uma medida da atração média entre as partículas,

${\ displaystyle b = N _ {\ text {A}} b '}$

é o volume excluído por um mol de partículas,

${\ displaystyle n = N / N _ {\ text {A}}}$

é o número de moles,

${\ displaystyle R = N _ {\ text {A}} k _ {\ text {B}}}$

é a constante universal de gás , k _B é a constante de Boltzmann e N _A é a constante de Avogadro .

Uma distinção cuidadosa deve ser traçada entre o volume disponível para uma partícula e o volume de uma partícula. Na equação intensiva, v é igual ao espaço total disponível para cada partícula, enquanto o parâmetro b ′ é proporcional ao volume adequado de uma única partícula - o volume limitado pelo raio atômico . Isso é subtraído de v por causa do espaço ocupado por uma partícula. Na derivação original de Van der Waals, dada abaixo, b ' é quatro vezes o volume adequado da partícula. Observe ainda que a pressão p vai ao infinito quando o recipiente está completamente cheio de partículas, de modo que não há espaço vazio para as partículas se moverem; isso ocorre quando V = nb .

Mistura de gás

Se uma mistura de gases está sendo considerada, e cada gás tem seus próprios valores (atração entre as moléculas) e (volume ocupado pelas moléculas), então e para a mistura pode ser calculado como ${\ displaystyle n}$${\ displaystyle a}$${\ displaystyle b}$${\ displaystyle a}$${\ displaystyle b}$

${\ displaystyle m}$ = número total de mols de gás presente,

para cada um , = número de moles de gás presente, e ${\ displaystyle i}$${\ displaystyle m_ {i}}$${\ displaystyle i}$${\ displaystyle x_ {i} = {\ frac {m_ {i}} {m}}}$

${\ displaystyle a = \ sum _ {i = 1} ^ {i = n} \ sum _ {j = 1} ^ {i = n} (x_ {i} x_ {j} {\ sqrt {a_ {i} a_ {j}}})}$

${\ displaystyle b = \ sum _ {i = 1} ^ {i = n} \ sum _ {j = 1} ^ {i = n} (x_ {i} x_ {j} {\ sqrt {b_ {i} b_ {j}}})}$

e a regra de adicionar pressões parciais torna-se inválida se o resultado numérico da equação for significativamente diferente da equação do gás ideal . ${\ displaystyle \ left (p + ({n ^ {2} a} / {V ^ {2}}) \ right) \ left (V-nb \ right) = nRT}$ ${\ displaystyle pV = nRT}$

Forma reduzida

A equação de Van der Waals também pode ser expressa em termos de propriedades reduzidas :

${\ displaystyle \ left (P_ {r} + {\ frac {3} {V_ {r} ^ {2}}} \ right) \ left (V_ {r} - {\ frac {1} {3}} \ direita) = {\ frac {8} {3}} T_ {r}}$

Isso resulta em um fator crítico de compressibilidade de 3/8. Razões para a modificação da equação do gás ideal: O estado da equação para o gás ideal é PV = RT. Na derivação das leis dos gases ideais com base na teoria cinética dos gases, algumas suposições foram feitas.

Validade

A equação de Van der Waals é matematicamente simples, mas, no entanto, prevê a transição experimentalmente observada entre o vapor e o líquido e prevê o comportamento crítico . Também prevê e explica adequadamente o efeito Joule-Thomson (mudança de temperatura durante a expansão adiabática), o que não é possível no gás ideal.

Acima da temperatura crítica , T _C , a equação de Van der Waals é uma melhoria em relação à lei dos gases ideais, e para temperaturas mais baixas, ou seja, T < T _C , a equação também é qualitativamente razoável para os estados líquido e gasoso de baixa pressão; no entanto, no que diz respeito à transição de fase de primeira ordem, ou seja, a faixa de ( p, V, T ) onde uma fase líquida e uma fase gasosa estariam em equilíbrio, a equação parece falhar em prever o comportamento experimental observado, no sentido que p é tipicamente observado como constante em função de V para uma dada temperatura na região de duas fases. Esta aparente discrepância é resolvida no contexto do equilíbrio líquido-vapor: em uma determinada temperatura, existem dois pontos na isoterma de Van der Waals que têm o mesmo potencial químico e, portanto, um sistema em equilíbrio termodinâmico parecerá atravessar uma linha reta no diagrama p - V conforme a proporção de vapor para líquido muda. No entanto, em tal sistema, existem realmente apenas dois pontos presentes (o líquido e o vapor) em vez de uma série de estados conectados por uma linha, portanto, conectar o local dos pontos é incorreto: não é uma equação de múltiplos estados, mas uma equação de (um único) estado. De fato, é possível comprimir um gás além do ponto em que ele normalmente se condensaria, dadas as condições certas, e também é possível expandir um líquido além do ponto em que normalmente ferveria. Esses estados são chamados de estados "metaestáveis". Tal comportamento é qualitativamente (embora talvez não quantitativamente) previsto pela equação de estado de Van der Waals.

No entanto, os valores das grandezas físicas conforme preditos com a equação de estado de Van der Waals "estão em péssimo acordo com o experimento", de modo que a utilidade do modelo é limitada a propósitos qualitativos em vez de quantitativos. Correções com base empírica podem ser facilmente inseridas no modelo de Van der Waals (veja a correção de Maxwell , abaixo), mas, ao fazer isso, a expressão modificada não é mais um modelo analítico simples; a este respeito, outros modelos, como aqueles baseados no princípio dos estados correspondentes , conseguem um melhor ajuste com aproximadamente o mesmo trabalho. Mesmo com suas deficiências reconhecidas, o uso difundido da equação de Van der Waals em livros-texto universitários de físico-química deixa clara sua importância como uma ferramenta pedagógica para auxiliar a compreensão de ideias de físico-química fundamentais envolvidas no desenvolvimento de teorias de comportamento vapor-líquido e equações de estado. Além disso, outras equações de estado (mais precisas), como a equação de estado de Redlich – Kwong e Peng – Robinson, são essencialmente modificações da equação de estado de Van der Waals.

Derivação

Os livros de físico-química geralmente fornecem duas derivações da equação do título. Uma é a derivação convencional que remonta a Van der Waals, uma equação de estado mecânica que não pode ser usada para especificar todas as funções termodinâmicas; a outra é uma derivação da mecânica estatística que torna explícito o potencial intermolecular negligenciado na primeira derivação. Uma vantagem particular da derivação mecânica estatística é que ela produz a função de partição para o sistema e permite que todas as funções termodinâmicas sejam especificadas (incluindo a equação de estado mecânica).

Derivação convencional

Considere um mol de gás composto de partículas pontuais não interagentes que satisfazem a lei dos gases ideais: (consulte qualquer texto padrão de Química Física, op. Cit.)

${\ displaystyle p = {\ frac {RT} {V _ {\ mathrm {m}}}}.}$

Em seguida, assuma que todas as partículas são esferas duras do mesmo raio finito r (o raio de Van der Waals ). O efeito do volume finito das partículas é diminuir o espaço vazio disponível no qual as partículas estão livres para se mover. Devemos substituir V por V  -  b , onde b é chamado de volume excluído (por mol) ou "co-volume". A equação corrigida torna-se

${\ displaystyle p = {\ frac {RT} {V _ {\ mathrm {m}} -b}}.}$

O volume excluído não é apenas igual ao volume ocupado pelas partículas sólidas de tamanho finito, mas na verdade quatro vezes o volume molecular total para um mol de um gás de Van der waals. Para ver isso, devemos perceber que uma partícula é circundada por uma esfera de raio 2 r (duas vezes o raio original) que é proibida para os centros das outras partículas. Se a distância entre os centros de duas partículas fosse menor que 2 r , isso significaria que as duas partículas se penetram, o que, por definição, as esferas duras são incapazes de fazer. ${\ displaystyle b}$

O volume excluído para as duas partículas (de diâmetro médio d ou raio r ) é

${\ displaystyle b '_ {2} = 4 \ pi d ^ {3} / 3 = 8 \ vezes (4 \ pi r ^ {3} / 3)}$ ,

que, dividido por dois (o número de partículas em colisão), dá o volume excluído por partícula:

${\ displaystyle b '= b' _ {2} / 2 \ quad \ rightarrow \ quad b '= 4 \ vezes (4 \ pi r ^ {3} / 3)}$ ,

Portanto, b ′ é quatro vezes o volume adequado da partícula. Era um ponto de preocupação para Van der Waals que o fator quatro produzisse um limite superior; os valores empíricos para b ′ são geralmente mais baixos. É claro que as moléculas não são infinitamente duras, como pensava Van der Waals, e muitas vezes são bastante moles. Para obter o volume excluído por mol, precisamos apenas multiplicar pelo número de moléculas em uma mol, ou seja, pelo número avogadro:

${\ displaystyle b = N_ {A} b '}$ .

Em seguida, introduzimos uma força atrativa (não necessariamente emparelhada) entre as partículas. Van der Waals assumiu que, apesar da existência dessa força, a densidade do fluido é homogênea; além disso, ele presumiu que o alcance da força de atração é tão pequeno que a grande maioria das partículas não sente que o recipiente é de tamanho finito. Dada a homogeneidade do fluido, o volume das partículas não sofre uma força resultante que as puxa para a direita ou para a esquerda. Isso é diferente para as partículas nas camadas superficiais diretamente adjacentes às paredes. Eles sentem uma força resultante das partículas a granel puxando-os para o recipiente, porque essa força não é compensada por partículas no lado onde a parede está (outra suposição aqui é que não há interação entre paredes e partículas, o que não é verdade, como pode ser visto a partir do fenômeno de formação de gotículas; a maioria dos tipos de líquido apresenta adesão). Esta rede de força diminui a força exercida na parede pelas partículas na camada superficial. A força resultante em uma partícula superficial, puxando-a para dentro do recipiente, é proporcional à densidade numérica. Ao considerar um mol de gás, o número de partículas será N _A

${\ displaystyle C = N _ {\ mathrm {A}} / V _ {\ mathrm {m}}}$ .

O número de partículas nas camadas superficiais é, novamente assumindo homogeneidade, também proporcional à densidade. No total, a força nas paredes é diminuída por um fator proporcional ao quadrado da densidade, e a pressão (força por unidade de superfície) é diminuída em

${\ displaystyle a'C ^ {2} = a '\ left ({\ frac {N _ {\ mathrm {A}}} {V _ {\ mathrm {m}}}} \ right) ^ {2} = {\ frac {a} {V _ {\ mathrm {m}} ^ {2}}}}$ ,

de modo a

${\ displaystyle p = {\ frac {RT} {V _ {\ mathrm {m}} -b}} - {\ frac {a} {V _ {\ mathrm {m}} ^ {2}}} \ Rightarrow \ left (p + {\ frac {a} {V _ {\ mathrm {m}} ^ {2}}} \ direita) (V _ {\ mathrm {m}} -b) = RT.}$

Ao escrever n para o número de moles e nV _m = V , a equação obtém a segunda forma dada acima,

${\ displaystyle \ left (p + {\ frac {n ^ {2} a} {V ^ {2}}} \ right) (V-nb) = nRT.}$

É de algum interesse histórico apontar que Van der Waals, em sua palestra com o Prêmio Nobel, deu crédito a Laplace pelo argumento de que a pressão é reduzida proporcionalmente ao quadrado da densidade.

Derivação da termodinâmica estatística

A função de partição canônica Z de um gás ideal que consiste em N = nN _A partículas idênticas ( não interagentes ) é:

${\ displaystyle Z = {\ frac {z ^ {N}} {N!}} \ quad {\ hbox {com}} \ quad z = {\ frac {V} {\ Lambda ^ {3}}}}$

onde é o comprimento de onda térmico de Broglie , ${\ displaystyle \ Lambda}$

${\ displaystyle \ Lambda = {\ sqrt {\ frac {h ^ {2}} {2 \ pi mkT}}}}$

com as definições usuais: h é a constante de Planck , m a massa de uma partícula, k constante de Boltzmann e T a temperatura absoluta. Em um gás ideal z é a função de partição de uma única partícula num recipiente de volume V . Para derivar a equação de Van der Waals, assumimos agora que cada partícula se move independentemente em um campo potencial médio oferecido pelas outras partículas. A média das partículas é fácil porque assumiremos que a densidade das partículas do fluido de Van der Waals é homogênea. A interação entre um par de partículas, que são esferas duras, é considerada

${\ displaystyle u (r) = {\ begin {cases} \ infty & {\ hbox {when}} \ quad r <d, \\ - \ epsilon \ left ({\ frac {d} {r}} \ right ) ^ {6} & {\ hbox {quando}} \ quad r \ geq d, \ end {casos}}}$

r é a distância entre os centros das esferas ed é a distância onde as esferas duras se tocam (duas vezes o raio de Van der Waals). A profundidade do poço Van der Waals é . ${\ displaystyle \ epsilon}$

Como as partículas não estão acopladas sob o campo hamiltoniano médio, a aproximação do campo médio da função de partição total ainda fatoriza,

${\ displaystyle Z = z ^ {N} / N!}$ ,

mas o potencial intermolecular necessita de duas modificações para z . Primeiro, por causa do tamanho finito das partículas, nem todo V está disponível, mas apenas V - Nb ' , onde (assim como na derivação convencional acima)

${\ displaystyle b '= 2 \ pi d ^ {3} / 3}$ .

Em segundo lugar, inserimos um fator de Boltzmann exp [ - ϕ / 2kT ] para cuidar do potencial intermolecular médio. Dividimos aqui o potencial por dois porque essa energia de interação é compartilhada entre duas partículas. Desse modo

${\ displaystyle z = {\ frac {(V-Nb ') \, e ^ {- \ phi / (2kT)}} {\ Lambda ^ {3}}}.}$

A atração total sentida por uma única partícula é

${\ displaystyle \ phi = \ int _ {d} ^ {\ infty} u (r) {\ frac {N} {V}} 4 \ pi r ^ {2} dr,}$

onde assumimos que em uma casca de espessura d r existem N / V  4 π r ² dr partículas. Esta é uma aproximação de campo médio; a posição das partículas é calculada. Na realidade, a densidade próxima à partícula é diferente da densidade distante, como pode ser descrito por uma função de correlação de par. Além disso, é negligenciado que o fluido esteja encerrado entre paredes. Realizando a integral, obtemos

${\ displaystyle \ phi = -2a '{\ frac {N} {V}} \ quad {\ hbox {com}} \ quad a' = \ epsilon {\ frac {2 \ pi d ^ {3}} {3 }} = \ epsilon b '.}$

Portanto, obtemos,

${\ displaystyle \ ln Z = N \ ln {(V-Nb ')} + {\ frac {N ^ {2} a'} {VkT}} - N \ ln {(\ Lambda ^ {3})} - \ ln {N!}}$

Da termodinâmica estatística, sabemos que

${\ displaystyle p = kT {\ frac {\ partial \ ln Z} {\ partial V}}}$ ,

de modo que só temos que diferenciar os termos que contêm V. Obtemos

${\ displaystyle p = {\ frac {NkT} {V-Nb '}} - {\ frac {N ^ {2} a'} {V ^ {2}}} \ Rightarrow \ left (p + {\ frac {N ^ {2} a '} {V ^ {2}}} \ right) (V-Nb') = NkT \ Rightarrow \ left (p + {\ frac {n ^ {2} a} {V ^ {2}} } \ direita) (V-nb) = nRT.}$

Regra de área igual de Maxwell

Oscilação da isoterma de Van der Waals e áreas iguais de Maxwell. A regra de Maxwell elimina o comportamento oscilante da isoterma na zona de transição de fase, definindo-a como uma certa isobar naquela zona. A isotérmica acima é para uma temperatura reduzida de T _R = 0,9. A correção de Maxwell está em uma pressão de vapor de p _V ≈0,64700 entre o volume reduzido do líquido puro V _L ≈0,60340 e o gás puro V _G ≈2,3488 na pressão de vapor.

Abaixo da temperatura crítica, a equação de Van der Waals parece prever relações qualitativamente incorretas. Ao contrário dos gases ideais, as isotermas pV oscilam com um mínimo relativo ( d ) e um máximo relativo ( e ). Qualquer pressão entre p _d e p _e parece ter 3 volumes estáveis, contradizendo a observação experimental de que duas variáveis ​​de estado determinam completamente o estado de um sistema de um componente. Além disso, a compressibilidade isotérmica é negativa entre d e e (equivalentemente ), o que não pode descrever um sistema em equilíbrio. ${\ displaystyle \ scriptstyle \ left ({{\ partial P} / {\ partial V}} \ right) _ {T, N}> 0}$

Para resolver estes problemas, James Clerk Maxwell substituído a isotérmica entre os pontos de um e c com uma linha horizontal posicionada de modo que as áreas das duas regiões sombreadas seria igual (substituindo a um - d - ser - c curva com uma linha recta de a a c ); esta porção da isotérmica corresponde ao equilíbrio líquido-vapor. As regiões da isoterma de a - d e de c - e são interpretadas como estados metaestáveis ​​de líquido superaquecido e vapor super-resfriado, respectivamente. A regra de área igual pode ser expressa como:

${\ displaystyle p_ {V} (V_ {G} -V_ {L}) = \ int _ {V_ {L}} ^ {V_ {G}} p \, dV}$

onde p _V é a pressão de vapor (parte plana da curva), V _L é o volume da fase líquida pura no ponto a do diagrama e V _G é o volume da fase gasosa pura no ponto c do diagrama. Uma mistura de duas fases em p _V ocupará um volume total entre V _L e V _G , conforme determinado pela regra de alavanca de Maxwell .

Maxwell justificou a regra com base no fato de que a área em um diagrama pV corresponde ao trabalho mecânico, dizendo que o trabalho realizado no sistema na passagem de c para b deve ser igual ao trabalho liberado na passagem de a para b . Isso ocorre porque a mudança na energia livre A ( T , V ) é igual ao trabalho realizado durante um processo reversível e, como uma variável de estado , a energia livre deve ser independente do caminho. Em particular, o valor de A no ponto b deve ser o mesmo, independentemente de o caminho percorrido ser da esquerda ou da direita através da isobar horizontal, ou seguir a isoterma original de Van der Waals.

Essa derivação não é totalmente rigorosa, pois requer um caminho reversível por uma região de instabilidade termodinâmica, enquanto b é instável. Não obstante, as derivações modernas do potencial químico chegam à mesma conclusão, e continua sendo uma modificação necessária para os Van der Waals e para qualquer outra equação de estado analítica.

Do potencial químico

A regra de área igual de Maxwell também pode ser derivada de uma suposição de potencial químico igual μ das fases coexistentes de líquido e vapor. Na isoterma mostrada no gráfico acima, os pontos a e c são os únicos pares de pontos que cumprem a condição de equilíbrio de ter pressão, temperatura e potencial químico iguais. Conclui-se que os sistemas com volumes intermediários entre esses dois pontos consistirão em uma mistura do líquido puro e do gás com volumes específicos iguais às fases do líquido puro e do gás nos pontos a e c .

A equação de Van der Waals pode ser resolvida para V _L e V _L como funções da temperatura e da pressão de vapor p _V . Desde a:

${\ displaystyle p = - \ left ({\ frac {\ partial A} {\ partial V}} \ right) _ {T, N}}$

onde A é a energia livre de Helmholtz, segue-se que a regra de área igual pode ser expressa como:

${\ displaystyle p_ {V} = {\ frac {A (V_ {L}, T, N) -A (V_ {G}, T, N)} {V_ {G} -V_ {L}}}}$ é

Uma vez que os volumes de gás e líquido são funções de p _V e T apenas, esta equação é então resolvida numericamente para obter p _V em função da temperatura (e número de partículas N ), que pode então ser usado para determinar os volumes de gás e líquido .

Locus de coexistência para duas fases do fluido de Van der Waals

Um gráfico pseudo-3D do local dos volumes de líquido e vapor versus temperatura e pressão é mostrado na figura a seguir. Vê-se que os dois locii se encontram no ponto crítico (1,1,1) suavemente. Uma isotérmica do fluido de Van der Waals tomada em T _r = 0,90 também é mostrada, onde as interseções da isoterma com os locais ilustram a exigência do construto de que as duas áreas (vermelho e azul, mostradas) sejam iguais.

Outros parâmetros, formulários e aplicações

Outros parâmetros termodinâmicos

Reiteramos que o extenso volume V   está relacionado ao volume por partícula v = V / N   onde N = nN _A   é o número de partículas no sistema. A equação de estado não nos dá todos os parâmetros termodinâmicos do sistema. Podemos usar a equação para a energia de Helmholtz A

${\ displaystyle A = -kT \ ln Q. \,}$

A partir da equação derivada acima para ln Q , encontramos

${\ displaystyle A (T, V, N) = - NkT \ left [1+ \ ln \ left ({\ frac {(V-Nb ') T ^ {3/2}} {N \ Phi}} \ right ) \ right] - {\ frac {a'N ^ {2}} {V}}.}$

Onde Φ é uma constante indeterminada, que pode ser obtida da equação de Sackur-Tetrode para um gás ideal ser:

${\ displaystyle \ Phi = T ^ {3/2} \ Lambda ^ {3} = \ left ({\ frac {h} {\ sqrt {2 \ pi mk}}} \ right) ^ {3}}$

Essa equação expressa A   em termos de suas variáveis ​​naturais V   e T  e, portanto, nos dá todas as informações termodinâmicas sobre o sistema. A equação mecânica de estado já foi derivada acima

${\ displaystyle p = - \ left ({\ frac {\ partial A} {\ partial V}} \ right) _ {N, T} = {\ frac {NkT} {V-Nb '}} - {\ frac {a'N ^ {2}} {V ^ {2}}}.}$

A equação de estado de entropia produz a entropia ( S  )

${\ displaystyle S = - \ left ({\ frac {\ partial A} {\ partial T}} \ right) _ {N, V} = Nk \ left [\ ln \ left ({\ frac {(V-Nb ') T ^ {3/2}} {N \ Phi}} \ right) + {\ frac {5} {2}} \ right]}$

a partir da qual podemos calcular a energia interna

${\ displaystyle U = A + TS = {\ frac {3} {2}} \, NkT - {\ frac {a'N ^ {2}} {V}}.}$

Equações semelhantes podem ser escritas para o outro potencial termodinâmico e o potencial químico, mas expressar qualquer potencial em função da pressão p   exigirá a solução de um polinômio de terceira ordem, que produz uma expressão complicada. Portanto, expressar a entalpia e a energia de Gibbs como funções de suas variáveis ​​naturais será complicado.

Forma reduzida

Embora a constante de material de um e b sob a forma usual dos Van der Waals difere equação para cada fluido único considerado, a equação pode ser reformulado para uma forma invariante aplicável a todos os fluidos.

Definindo as seguintes variáveis ​​reduzidas ( f _R , f _C são as versões de variável reduzida e crítica de f , respectivamente),

${\ displaystyle p_ {R} = {\ frac {p} {p_ {C}}}, \ qquad v_ {R} = {\ frac {v} {v_ {C}}}, \ quad {\ hbox {e }} \ quad T_ {R} = {\ frac {T} {T_ {C}}}}$ ,

Onde

${\ displaystyle p_ {C} = {\ frac {a '} {27b' ^ {2}}}, \ qquad \ displaystyle {v_ {C} = 3b '}, \ quad {\ hbox {and}} \ quad kT_ {C} = {\ frac {8a '} {27b'}}}$

conforme mostrado por Salzman.

A primeira forma da equação de estado de Van der Waals dada acima pode ser reformulada na seguinte forma reduzida:

${\ displaystyle \ left (p_ {R} + {\ frac {3} {v_ {R} ^ {2}}} \ right) (3v_ {R} -1) = (8T_ {R}}$ )

Essa equação é invariável para todos os fluidos; isto é, a mesma equação de estado de forma reduzida se aplica, não importa o que a e b possam ser para o fluido em particular.

Essa invariância também pode ser entendida em termos do princípio dos estados correspondentes. Se dois fluidos têm a mesma pressão reduzida, volume reduzido e temperatura reduzida, dizemos que seus estados são correspondentes. Os estados de dois fluidos podem ser correspondentes mesmo se sua pressão, volume e temperatura medidos forem muito diferentes. Se os dois estados dos fluidos são correspondentes, eles existem no mesmo regime da equação de estado de forma reduzida. Portanto, eles responderão às mudanças mais ou menos da mesma maneira, embora suas características físicas mensuráveis ​​possam diferir significativamente.

Equação cúbica

A equação de Van der Waals é uma equação de estado cúbica ; na formulação reduzida, a equação cúbica é:

${\ displaystyle {v_ {R} ^ {3}} - {\ frac {1} {3}} \ left ({1 + {\ frac {8T_ {R}} {p_ {R}}}} \ right) {v_ {R} ^ {2}} + {\ frac {3} {p_ {R}}} v_ {R} - {\ frac {1} {p_ {R}}} = 0}$

Na temperatura crítica, onde chegamos conforme o esperado ${\ displaystyle T_ {R} = p_ {R} = 1}$

${\ displaystyle {v_ {R} ^ {3}} - 3v_ {R} ^ {2} + 3v_ {R} -1 = \ left (v_ {R} -1 \ right) ^ {3} = 0 \ quad \ Longleftrightarrow \ quad v_ {R} = 1}$

Para T _R <1, existem 3 valores para v _R . Para T _R > 1, há um valor real para v _R .

A solução desta equação para o caso em que existem três raízes separadas pode ser encontrada na construção de Maxwell

Aplicação a fluidos compressíveis

A equação também pode ser usada como uma equação PVT para fluidos compressíveis (por exemplo, polímeros ). Neste caso, as alterações de volume específicas são pequenas e podem ser escritas de forma simplificada:

${\ displaystyle (p + A) (VB) = CT, \,}$

onde p é a pressão , V é o volume específico , T é a temperatura e A, B, C são os parâmetros.

Veja também

• Leis de gás
• Gás ideal
• Temperatura de inversão
• Iteração
• Construção Maxwell
• Gás real
• Teorema de estados correspondentes
• Constantes de Van der Waals (página de dados)
• Equação de estado de Redlich-Kwong

Referências

Leitura adicional

• Chandler, David (1987). Introdução à Mecânica Estatística Moderna . Oxford: Oxford University Press. pp. 287–295. ISBN   0195042778 .
• Cross, Michael (2004), "Lecture 3: First Order Phase Transitions" (PDF) , Physics 127: Statistical Physics, Second Term , Pasadena, Califórnia: Divisão de Física, Matemática e Astronomia, California Institute of Technology .
• Dalgarno, A .; Davison, WD (1966). "O Cálculo das Interações de Van Der Waals". Avanços em Física Atômica e Molecular . 2 : 1-32. doi : 10.1016 / S0065-2199 (08) 60216-X . ISBN   9780120038022 .
• Kittel, Charles; Kroemer, Herbert (1980). Física Térmica (edição revisada). Nova York: Macmillan. pp. 287–295. ISBN   0716710889 .