Função de onda - Wave function

Comparação das concepções de oscilador harmônico quântico e clássico para uma única partícula sem spin. Os dois processos são muito diferentes. O processo clássico (A – B) é representado como o movimento de uma partícula ao longo de uma trajetória. O processo quântico (C – H) não tem essa trajetória. Em vez disso, é representado como uma onda; aqui, o eixo vertical mostra a parte real (azul) e a parte imaginária (vermelha) da função de onda. Os painéis (C – F) mostram quatro soluções diferentes de ondas estacionárias da equação de Schrödinger . Os painéis (G – H) mostram ainda duas funções de onda diferentes que são soluções da equação de Schrödinger, mas não ondas estacionárias.

Uma função de onda na física quântica é uma descrição matemática do estado quântico de um sistema quântico isolado . A função de onda é uma amplitude de probabilidade de valor complexo , e as probabilidades para os possíveis resultados de medições feitas no sistema podem ser derivadas dela. Os símbolos mais comuns para uma função de onda são as letras gregas $ψ$ e $Ψ$ (minúsculas e maiúsculas psi , respectivamente).

A função de onda é uma função dos graus de liberdade correspondentes a algum conjunto máximo de observáveis de comutação . Uma vez que tal representação é escolhida, a função de onda pode ser derivada do estado quântico.

Para um determinado sistema, a escolha de quais graus de liberdade de comutação usar não é única e, correspondentemente, o domínio da função de onda também não é único. Por exemplo, pode ser considerado uma função de todas as coordenadas de posição das partículas sobre o espaço de posição, ou os momentos de todas as partículas sobre o espaço de momento ; os dois estão relacionados por uma transformada de Fourier . Algumas partículas, como elétrons e fótons , têm spin diferente de zero , e a função de onda para tais partículas inclui spin como um grau de liberdade discreto intrínseco; outras variáveis discretas também podem ser incluídas, como isospin . Quando um sistema tem graus de liberdade internos, a função de onda em cada ponto nos graus de liberdade contínuos (por exemplo, um ponto no espaço) atribui um número complexo para cada valor possível dos graus de liberdade discretos (por exemplo, componente z de spin) - esses valores são freqüentemente exibidos em uma matriz de coluna (por exemplo, um vetor de coluna $2 \times 1$ para um elétron não relativístico com spin $.mw-parser-output .frac{white-space:nowrap}.mw-parser-output .frac .num,.mw-parser-output .frac .den{font-size:80%;line-height:0;vertical-align:super}.mw-parser-output .frac .den{vertical-align:sub}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px} 1 ⁄ 2$ ).

De acordo com o princípio de superposição da mecânica quântica, as funções de onda podem ser somadas e multiplicadas por números complexos para formar novas funções de onda e formar um espaço de Hilbert . O produto interno entre duas funções de onda é uma medida da sobreposição entre os estados físicos correspondentes e é usado na interpretação probabilística fundamental da mecânica quântica, a regra de Born , relacionando as probabilidades de transição aos produtos internos. A equação de Schrödinger determina como as funções de onda evoluem ao longo do tempo, e uma função de onda se comporta qualitativamente como outras ondas , como ondas de água ou ondas em uma corda, porque a equação de Schrödinger é matematicamente um tipo de equação de onda . Isso explica o nome "função de onda" e dá origem à dualidade onda-partícula . No entanto, a função de onda na mecânica quântica descreve uma espécie de fenômeno físico, ainda aberto a diferentes interpretações , que difere fundamentalmente das ondas mecânicas clássicas .

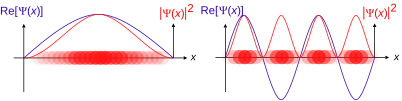
Na interpretação estatística de Born na mecânica quântica não relativística, o módulo quadrado da função de onda, $| ψ | 2$ , é um número real interpretado como a densidade de probabilidade de medir uma partícula como estando em um determinado lugar - ou tendo um determinado momento - em um determinado momento, e possivelmente tendo valores definidos para graus de liberdade discretos. A integral dessa quantidade, sobre todos os graus de liberdade do sistema, deve ser 1 de acordo com a interpretação da probabilidade. Este requisito geral que uma função de onda deve satisfazer é chamado de condição de normalização . Uma vez que a função de onda tem um valor complexo, apenas sua fase relativa e magnitude relativa podem ser medidas - seu valor, isoladamente, não diz nada sobre as magnitudes ou direções de observáveis mensuráveis; deve-se aplicar operadores quânticos , cujos autovalores correspondem a conjuntos de possíveis resultados de medições, à função de onda $ψ$ e calcular as distribuições estatísticas para grandezas mensuráveis.

Contexto histórico

Em 1905, Albert Einstein postulou a proporcionalidade entre a frequência de um fóton e sua energia , , e em 1916 a relação correspondente entre um fóton impulso e comprimento de onda , , onde é a constante de Planck . Em 1923, De Broglie foi o primeiro a sugerir que a relação , agora chamada de relação De Broglie , vale para partículas massivas , a pista principal sendo a invariância de Lorentz , e isso pode ser visto como o ponto de partida para o desenvolvimento moderno da mecânica quântica. As equações representam a dualidade onda-partícula para partículas massivas e sem massa. ${\ displaystyle f}$ ${\ displaystyle E}$ ${\ displaystyle E = hf}$ ${\ displaystyle p}$ ${\ displaystyle \ lambda}$ ${\ displaystyle \ lambda = {\ frac {h} {p}}}$ ${\ displaystyle h}$ ${\ displaystyle \ lambda = {\ frac {h} {p}}}$

Nas décadas de 1920 e 1930, a mecânica quântica foi desenvolvida usando cálculo e álgebra linear . Aqueles que usaram as técnicas de cálculo incluíram Louis de Broglie , Erwin Schrödinger e outros, desenvolvendo a " mecânica ondulatória ". Aqueles que aplicaram os métodos de álgebra linear incluíram Werner Heisenberg , Max Born e outros, desenvolvendo a "mecânica matricial". Schrödinger posteriormente mostrou que as duas abordagens eram equivalentes.

Em 1926, Schrödinger publicou a famosa equação de onda agora nomeada em sua homenagem, a equação de Schrödinger . Esta equação foi baseada na conservação clássica de energia usando operadores quânticos e as relações de de Broglie, e as soluções da equação são as funções de onda para o sistema quântico. No entanto, ninguém sabia como interpretá-lo . No início, Schrödinger e outros pensaram que as funções de onda representam partículas que se espalham, estando a maior parte da partícula onde a função de onda é grande. Isso se mostrou incompatível com o espalhamento elástico de um pacote de ondas (representando uma partícula) para fora de um alvo; ele se espalha em todas as direções. Embora uma partícula espalhada possa se espalhar em qualquer direção, ela não se divide e decola em todas as direções. Em 1926, Born forneceu a perspectiva da amplitude de probabilidade . Isso relaciona os cálculos da mecânica quântica diretamente às observações experimentais probabilísticas. É aceito como parte da interpretação de Copenhague da mecânica quântica. Existem muitas outras interpretações da mecânica quântica . Em 1927, Hartree e Fock deram o primeiro passo na tentativa de resolver a função de onda de N- corpo e desenvolveram o ciclo de autoconsistência : um algoritmo iterativo para aproximar a solução. Agora também é conhecido como método Hartree-Fock . O determinante e permanente de Slater (de uma matriz ) fazia parte do método, fornecido por John C. Slater .

Schrödinger encontrou uma equação para a função de onda que satisfazia a conservação de energia relativística antes de publicar a não relativística, mas a descartou porque previa probabilidades negativas e energias negativas . Em 1927, Klein , Gordon e Fock também o encontraram, mas incorporaram a interação eletromagnética e provaram que era invariante de Lorentz . De Broglie também chegou à mesma equação em 1928. Essa equação de onda relativística é agora mais comumente conhecida como equação de Klein-Gordon .

Em 1927, Pauli fenomenologicamente encontrou uma equação não relativística para descrever partículas de spin 1/2 em campos eletromagnéticos, agora chamada de equação de Pauli . Pauli descobriu que a função de onda não era descrita por uma única função complexa de espaço e tempo, mas precisava de dois números complexos, que correspondem respectivamente aos estados de spin +1/2 e -1/2 do férmion. Logo depois, em 1928, Dirac encontrou uma equação da primeira unificação bem-sucedida da relatividade especial e da mecânica quântica aplicada ao elétron , agora chamada de equação de Dirac . Nesse caso, a função de onda é um espinor representado por quatro componentes de valor complexo: dois para o elétron e dois para a antipartícula do elétron , o pósitron . No limite não relativístico, a função de onda de Dirac se assemelha à função de onda de Pauli para o elétron. Mais tarde, outras equações de onda relativísticas foram encontradas.

Funções de onda e equações de onda em teorias modernas

Todas essas equações de onda são de importância duradoura. A equação de Schrödinger e a equação de Pauli são, em muitas circunstâncias, excelentes aproximações das variantes relativísticas. Eles são consideravelmente mais fáceis de resolver em problemas práticos do que as contrapartes relativísticas.

A equação de Klein-Gordon e a equação de Dirac , embora sejam relativísticas, não representam a reconciliação completa da mecânica quântica e da relatividade especial. O ramo da mecânica quântica onde essas equações são estudadas da mesma maneira que a equação de Schrödinger, frequentemente chamada de mecânica quântica relativística , embora muito bem-sucedida, tem suas limitações (ver, por exemplo, o deslocamento de Lamb ) e problemas conceituais (ver, por exemplo, o mar de Dirac ).

A relatividade torna inevitável que o número de partículas em um sistema não seja constante. Para uma reconciliação completa, a teoria quântica de campos é necessária. Nesta teoria, as equações de onda e as funções de onda têm seu lugar, mas em uma aparência um pouco diferente. Os principais objetos de interesse não são as funções de onda, mas sim os operadores, os chamados operadores de campo (ou apenas campos onde "operador" é entendido) no espaço de estados de Hilbert (a ser descrito na próxima seção). Acontece que as equações de onda relativísticas originais e suas soluções ainda são necessárias para construir o espaço de Hilbert. Além disso, os operadores de campos livres , isto é, quando se assume que as interações não existem, acabam por satisfazer (formalmente) a mesma equação que os campos (funções de onda) em muitos casos.

Assim, a equação de Klein-Gordon (spin $0$ ) e a equação de Dirac (spin $1 ⁄ 2$ ) sob esse aspecto permanecem na teoria. Os análogos de spin mais altos incluem a equação de Proca (spin $1$ ), a equação de Rarita-Schwinger (spin $3 ⁄ 2$ ) e, de forma mais geral, as equações de Bargmann-Wigner . Para campos livres sem massa , dois exemplos são a equação de Maxwell de campo livre (spin $1$ ) e a equação de Einstein de campo livre (spin $2$ ) para os operadores de campo. Todos eles são essencialmente uma consequência direta do requisito de invariância de Lorentz . Suas soluções devem se transformar sob a transformação de Lorentz de uma forma prescrita, ou seja, sob uma representação particular do grupo de Lorentz e que junto com algumas outras demandas razoáveis, por exemplo, o princípio de decomposição de cluster , com implicações para a causalidade, é suficiente para corrigir as equações.

Isso se aplica a equações de campo livre; as interações não são incluídas. Se uma densidade Lagrangiana (incluindo interações) estiver disponível, o formalismo Lagrangeano produzirá uma equação de movimento no nível clássico. Essa equação pode ser muito complexa e não passível de solução. Qualquer solução se referiria a um número fixo de partículas e não levaria em conta o termo "interação" como referido nessas teorias, que envolve a criação e aniquilação de partículas e não de potenciais externos como na teoria quântica "primeiro quantizada" comum.

Na teoria das cordas , a situação permanece análoga. Por exemplo, uma função de onda no espaço de momento tem o papel do coeficiente de expansão de Fourier em um estado geral de uma partícula (corda) com momento que não é definido nitidamente.

Definição (uma partícula sem spin em uma dimensão)

Ondas estacionárias para uma partícula em uma caixa , exemplos de estados estacionários .

Ondas itinerantes de uma partícula livre.

As partes reais da função de onda de posição

Ψ (x)

e da função de onda de momento

Φ (p)

, e as densidades de probabilidade correspondentes

| Ψ (x) | 2

e

| Φ (p) | 2

, para uma partícula de spin-0 em uma dimensão

x

ou

p

. A opacidade de cor das partículas corresponde à densidade de probabilidade ( não a função de onda) de encontrar a partícula na posição

x

ou momento

p

.

Por enquanto, considere o caso simples de uma única partícula não relativística, sem spin , em uma dimensão espacial. Casos mais gerais são discutidos abaixo.

Funções de onda espacial de posição

O estado de tal partícula é completamente descrito por sua função de onda,

{\ displaystyle \ Psi (x, t) \ ,,}

onde $x$ é a posição e $t$ é o tempo. Esta é uma função de valor complexo de duas variáveis reais $x$ e $t$ .

Para uma partícula sem spin em uma dimensão, se a função de onda for interpretada como uma amplitude de probabilidade , o módulo quadrado da função de onda, o número real positivo

{\ displaystyle \ left | \ Psi (x, t) \ right | ^ {2} = \ Psi ^ {*} (x, t) \ Psi (x, t) = \ rho (x, t),}

é interpretado como a densidade de probabilidade de que a partícula esteja em $x$ . O asterisco indica o conjugado complexo . Se a posição da partícula é medida , sua localização não pode ser determinada a partir da função de onda, mas é descrita por uma distribuição de probabilidade .

Condição de normalização

A probabilidade de que sua posição $x$ esteja no intervalo $a \leq x \leq b$ é a integral da densidade ao longo deste intervalo:

{\ displaystyle P_ {a \ leq x \ leq b} (t) = \ int _ {a} ^ {b} \, | \ Psi (x, t) | ^ {2} dx}

onde $t$ é o momento em que a partícula foi medida. Isso leva à condição de normalização :

{\ displaystyle \, \ int _ {- \ infty} ^ {\ infty} \, | \ Psi (x, t) | ^ {2} dx = 1 \ ,,}

porque se a partícula for medida, há 100% de probabilidade de que ela esteja em algum lugar .

Para um determinado sistema, o conjunto de todas as funções de onda normalizáveis possíveis (em qualquer momento) forma um espaço vetorial matemático abstrato , o que significa que é possível somar diferentes funções de onda e multiplicar funções de onda por números complexos (ver espaço vetorial para detalhes). Tecnicamente, por causa da condição de normalização, as funções de onda formam um espaço projetivo em vez de um espaço vetorial comum. Este espaço vetorial é infinito- dimensional , porque não existe um conjunto finito de funções que podem ser somadas em várias combinações para criar todas as funções possíveis. Além disso, é um espaço de Hilbert , porque o produto interno de duas funções de onda $Ψ 1$ e $Ψ 2$ pode ser definido como o número complexo (no tempo $t$ )

{\ displaystyle (\ Psi _ {1}, \ Psi _ {2}) = \ int _ {- \ infty} ^ {\ infty} \, \ Psi _ {1} ^ {*} (x, t) \ Psi _ {2} (x, t) dx.}

Mais detalhes são fornecidos abaixo . Embora o produto interno de duas funções de onda seja um número complexo, o produto interno de uma função de onda $Ψ$ consigo mesmo,

{\ displaystyle (\ Psi, \ Psi) = \ | \ Psi \ | ^ {2} \ ,,}

é sempre um número real positivo. O número $|| Ψ ||$ (não $|| Ψ || 2$ ) é chamada de norma da função de onda $Ψ$ .

Se $(Ψ, Ψ) = 1$ , então $Ψ$ é normalizado. Se $Ψ$ não é normalizado, então dividindo por sua norma dá a função normalizada $Ψ / || Ψ ||$ . Duas funções de onda $Ψ 1$ e $Ψ 2$ são ortogonais se $(Ψ 1, Ψ 2) = 0$ . Se forem normalizados e ortogonais, são ortonormais . A ortogonalidade (daí também a ortonormalidade) das funções de onda não é uma condição necessária que as funções de onda devem satisfazer, mas é instrutivo a se considerar, uma vez que garante a independência linear das funções. Em uma combinação linear de funções de onda ortogonais $Ψ n$ temos,

{\ displaystyle \ Psi = \ sum _ {n} a_ {n} \ Psi _ {n} \ ,, \ quad a_ {n} = {\ frac {(\ Psi _ {n}, \ Psi)} {( \ Psi _ {n}, \ Psi _ {n})}}}

Se as funções de onda $Ψ n$ fossem não ortogonais, os coeficientes seriam menos simples de obter.

Estados quânticos como vetores

Na interpretação de Copenhagen , o módulo ao quadrado do produto interno (um número complexo) fornece um número real

{\ displaystyle \ left | (\ Psi _ {1}, \ Psi _ {2}) \ right | ^ {2} = P \ left (\ Psi _ {2} \ rightarrow \ Psi _ {1} \ right) \ ,,}

que, assumindo que ambas as funções de onda estão normalizadas, é interpretado como a probabilidade da função de onda $Ψ 2$ "colapsar" para a nova função de onda $Ψ 1$ após a medição de um observável, cujos autovalores são os resultados possíveis da medição, com $Ψ 1$ sendo um autovetor do autovalor resultante. Essa é a regra de Born e um dos postulados fundamentais da mecânica quântica.

Em um determinado instante de tempo, todos os valores da função de onda $Ψ (x, t)$ são componentes de um vetor. Existem incontáveis e infinitamente muitos deles e a integração é usada no lugar da soma. Na notação Bra-ket , este vetor é escrito

{\ displaystyle | \ Psi (t) \ rangle = \ int \ Psi (x, t) | x \ rangle dx}

e é referido como um "vetor de estado quântico" ou simplesmente "estado quântico". Existem várias vantagens para compreender as funções de onda como elementos representativos de um espaço vetorial abstrato:

Todas as ferramentas poderosas da álgebra linear podem ser usadas para manipular e compreender funções de onda. Por exemplo:
- A álgebra linear explica como um espaço vetorial pode receber uma base , e então qualquer vetor no espaço vetorial pode ser expresso nesta base. Isso explica a relação entre uma função de onda no espaço de posição e uma função de onda no espaço de momento e sugere que também existem outras possibilidades.
- A notação de bra-ket pode ser usada para manipular funções de onda.
A ideia de que os estados quânticos são vetores em um espaço vetorial abstrato é completamente geral em todos os aspectos da mecânica quântica e da teoria quântica de campos , enquanto a ideia de que os estados quânticos são funções de "onda" de valor complexo do espaço só é verdadeira em certas situações.

O parâmetro de tempo é freqüentemente suprimido e será o seguinte. A coordenada $x$ é um índice contínuo. O $| x ⟩$ são os vectores de base, que são ortonormais pelo que a sua produto interior é uma função delta ;

{\ displaystyle \ langle x '| x \ rangle = \ delta (x'-x)}

portanto

{\ displaystyle \ langle x '| \ Psi \ rangle = \ int \ Psi (x) \ langle x' | x \ rangle dx = \ Psi (x ')}

e

{\ displaystyle | \ Psi \ rangle = \ int | x \ rangle \ langle x | \ Psi \ rangle dx = \ left (\ int | x \ rangle \ langle x | dx \ right) | \ Psi \ rangle}

que ilumina o operador de identidade

{\ displaystyle I = \ int | x \ rangle \ langle x | dx \ ,.}

Encontrar o operador de identidade em uma base permite que o estado abstrato seja expresso explicitamente em uma base, e mais (o produto interno entre dois vetores de estado e outros operadores para observáveis podem ser expressos na base).

Funções de onda espaço-momentum

A partícula também tem uma função de onda no espaço de momento :

{\ displaystyle \ Phi (p, t)}

onde $p$ é o momento em uma dimensão, que pode ser qualquer valor de $-\infty$ a $+ \infty$ , e $t$ é o tempo.

Analogamente ao caso de posição, o produto interno de duas funções de onda $Φ 1 (p, t)$ e $Φ 2 (p, t)$ pode ser definido como:

{\ displaystyle (\ Phi _ {1}, \ Phi _ {2}) = \ int _ {- \ infty} ^ {\ infty} \, \ Phi _ {1} ^ {*} (p, t) \ Phi _ {2} (p, t) dp \ ,.}

Uma solução particular para a equação de Schrödinger independente do tempo é

{\ displaystyle \ Psi _ {p} (x) = e ^ {ipx / \ hbar},}

uma onda plana , que pode ser usada na descrição de uma partícula com momento exatamente $p$ , uma vez que é uma autofunção do operador momento. Essas funções não são normalizáveis para a unidade (não são integráveis ao quadrado), portanto, não são realmente elementos do espaço físico de Hilbert. O conjunto

{\ displaystyle \ {\ Psi _ {p} (x, t), - \ infty \ leq p \ leq \ infty \}}

forma o que é chamado de base de momentum . Essa "base" não é uma base no sentido matemático usual. Por um lado, uma vez que as funções não são normalizáveis, elas são normalizadas para uma função delta ,

{\ displaystyle (\ Psi _ {p}, \ Psi _ {p '}) = \ delta (p-p').}

Por outro lado, embora sejam linearmente independentes, há muitos deles (eles formam um conjunto incontável) para uma base para o espaço de Hilbert físico. Eles ainda podem ser usados para expressar todas as funções nele usando as transformadas de Fourier, conforme descrito a seguir.

Relações entre as representações de posição e momento

As representações $x$ e $p$ são

{\ displaystyle {\ begin {alinhados} | \ Psi \ rangle = I | \ Psi \ rangle & = \ int | x \ rangle \ langle x | \ Psi \ rangle dx = \ int \ Psi (x) | x \ rangle dx, \\ | \ Psi \ rangle = I | \ Psi \ rangle & = \ int | p \ rangle \ langle p | \ Psi \ rangle dp = \ int \ Phi (p) | p \ rangle dp. \ end { alinhado}}}

Agora tome a projeção do estado $Ψ$ em autofunções de momento usando a última expressão nas duas equações,

{\ displaystyle \ int \ Psi (x) \ langle p | x \ rangle dx = \ int \ Phi (p ') \ langle p | p' \ rangle dp '= \ int \ Phi (p') \ delta (p -p ') dp' = \ Phi (p).}

Em seguida, utilizando a expressão conhecida para estados próprios adequadamente normalizados de momento nas soluções de representação de posição da equação de Schrödinger livre

{\ displaystyle \ langle x | p \ rangle = p (x) = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} e ^ {{\ frac {i} {\ hbar}} px} \ Rightarrow \ langle p | x \ rangle = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} e ^ {- {\ frac {i} {\ hbar}} px},}

um obtém

{\ displaystyle \ Phi (p) = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} \ int \ Psi (x) e ^ {- {\ frac {i} {\ hbar}} px } dx \ ,.}

Da mesma forma, usando funções próprias de posição,

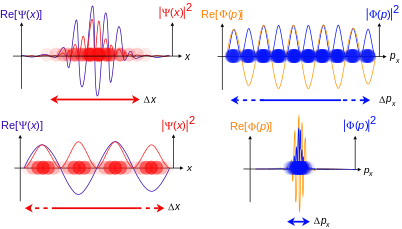
{\ displaystyle \ Psi (x) = {\ frac {1} {\ sqrt {2 \ pi \ hbar}}} \ int \ Phi (p) e ^ {{\ frac {i} {\ hbar}} px} dp \ ,.}

As funções de onda espaço-posição e espaço-momento são, portanto, transformadas de Fourier uma da outra. As duas funções de onda contêm as mesmas informações e qualquer uma delas sozinha é suficiente para calcular qualquer propriedade da partícula. Como representantes de elementos do espaço físico abstrato de Hilbert, cujos elementos são os estados possíveis do sistema em consideração, eles representam o mesmo vetor de estados, portanto estados físicos idênticos , mas geralmente não são iguais quando vistos como funções quadradas integráveis.

Na prática, a função de onda de espaço de posição é usada com muito mais freqüência do que a função de onda de espaço de momento. O potencial de entrada na equação relevante (Schrödinger, Dirac, etc.) determina em qual base a descrição é mais fácil. Para o oscilador harmônico , $x$ e $p$ entram simetricamente, portanto, não importa qual descrição se usa. Os resultados da mesma equação (constantes do módulo). Disto segue, com um pouco de reflexão posterior, um factóide: As soluções para a equação de onda do oscilador harmônico são autofunções da transformada de Fourier em $L 2$ .

Definições (outros casos)

A seguir estão as formas gerais da função de onda para sistemas em dimensões mais altas e mais partículas, bem como incluindo outros graus de liberdade além das coordenadas de posição ou componentes de momento.

Estados de uma partícula no espaço de posição 3d

A função de onda espaço-posição de uma única partícula sem spin em três dimensões espaciais é semelhante ao caso de uma dimensão espacial acima:

{\ displaystyle \ Psi (\ mathbf {r}, t)}

onde $r$ é o vetor posição no espaço tridimensional e $t$ é o tempo. Como sempre, $Ψ (r, t)$ é uma função de valor complexo de variáveis reais. Como um único vetor na notação de Dirac

{\ displaystyle | \ Psi (t) \ rangle = \ int d ^ {3} \! \ mathbf {r} \, \ Psi (\ mathbf {r}, t) \, | \ mathbf {r} \ rangle}

Todas as observações anteriores sobre produtos internos, funções de onda espacial de momento, transformadas de Fourier e assim por diante se estendem a dimensões superiores.

Para uma partícula com spin , ignorando os graus de liberdade da posição, a função de onda é uma função apenas do spin (o tempo é um parâmetro);

{\ displaystyle \ xi (s_ {z}, t)}

onde $s z$ é o número quântico da projeção de spin ao longo do eixo $z$ . (O eixo $z$ é uma escolha arbitrária; outros eixos podem ser usados se a função de onda for transformada apropriadamente, veja abaixo.) O parâmetro $s z$ , ao contrário de $r$ e $t$ , é uma variável discreta . Por exemplo, para uma partícula de spin-1/2 , $s z$ só pode ser $+1/2$ ou $-1/2$ , e não qualquer outro valor. (Em geral, para spin $s$ , $s z$ pode ser $s, s - 1,\dots, - s + 1, - s$ ). A inserção de cada número quântico dá uma função de valor complexa de espaço e tempo, há $2 s + 1$ deles. Eles podem ser organizados em um vetor de coluna

{\ displaystyle {\ xi = {\ begin {bmatrix} \ xi (s, t) \\\ xi (s-1, t) \\\ vdots \\\ xi (- (s-1), t) \ \\ xi (-s, t) \\\ end {bmatriz}} = \ xi (s, t) {\ begin {bmatrix} 1 \\ 0 \\\ vdots \\ 0 \\ 0 \\\ end { bmatrix}} + \ xi (s-1, t) {\ begin {bmatrix} 0 \\ 1 \\\ vdots \\ 0 \\ 0 \\\ end {bmatrix}} + \ cdots + \ xi (- ( s-1), t) {\ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 1 \\ 0 \\\ end {bmatrix}} + \ xi (-s, t) {\ begin {bmatrix} 0 \\ 0 \\\ vdots \\ 0 \\ 1 \\\ end {bmatrix}}}}

Na notação bra-ket , eles se organizam facilmente nos componentes de um vetor

{\ displaystyle | \ xi (t) \ rangle = \ sum _ {s_ {z} = - s} ^ {s} \ xi (s_ {z}, t) \, | s_ {z} \ rangle}

Todo o vetor $ξ$ é uma solução da equação de Schrödinger (com um hamiltoniano adequado), que se desdobra em um sistema acoplado de $2 s + 1$ equações diferenciais ordinárias com soluções $ξ (s, t), ξ (s - 1, t), \dots, Ξ (- s, t)$ . O termo "função de spin" em vez de "função de onda" é usado por alguns autores. Isso contrasta as soluções para posicionar as funções de onda espacial, as coordenadas de posição sendo graus de liberdade contínuos, porque então a equação de Schrödinger assume a forma de uma equação de onda.

De forma mais geral, para uma partícula em 3d com qualquer spin, a função de onda pode ser escrita em "espaço de rotação de posição" como:

{\ displaystyle \ Psi (\ mathbf {r}, s_ {z}, t)}

e estes também podem ser organizados em um vetor de coluna

{\ displaystyle \ Psi (\ mathbf {r}, t) = {\ begin {bmatrix} \ Psi (\ mathbf {r}, s, t) \\\ Psi (\ mathbf {r}, s-1, t ) \\\ vdots \\\ Psi (\ mathbf {r}, - (s-1), t) \\\ Psi (\ mathbf {r}, -s, t) \\\ end {bmatrix}}}

em que a dependência do spin é colocada na indexação das entradas, e a função de onda é uma função de valor vetorial complexa de espaço e tempo apenas.

Todos os valores da função de onda, não apenas para variáveis discretas, mas também contínuas, são coletados em um único vetor

{\ displaystyle | \ Psi (t) \ rangle = \ sum _ {s_ {z}} \ int d ^ {3} \! \ mathbf {r} \, \ Psi (\ mathbf {r}, s_ {z} , t) \, | \ mathbf {r}, s_ {z} \ rangle}

Para uma única partícula, o produto tensorial $\otimes$ de seu vetor de estado de posição $| ip ⟩$ e do estado de spin vector $| Ç ⟩$ dá o vector de estado de spin-posição compósito

{\ displaystyle | \ psi (t) \ rangle \! \ otimes \! | \ xi (t) \ rangle = \ sum _ {s_ {z}} \ int d ^ {3} \! \ mathbf {r} \ , \ psi (\ mathbf {r}, t) \, \ xi (s_ {z}, t) \, | \ mathbf {r} \ rangle \! \ otimes \! | s_ {z} \ rangle}

com as identificações

{\ displaystyle | \ Psi (t) \ rangle = | \ psi (t) \ rangle \! \ otimes \! | \ xi (t) \ rangle}

{\ displaystyle \ Psi (\ mathbf {r}, s_ {z}, t) = \ psi (\ mathbf {r}, t) \, \ xi (s_ {z}, t)}

{\ displaystyle | \ mathbf {r}, s_ {z} \ rangle = | \ mathbf {r} \ rangle \! \ otimes \! | s_ {z} \ rangle}

A fatoração do produto tensorial só é possível se os momentos orbitais e angulares de spin da partícula forem separáveis no operador hamiltoniano subjacente à dinâmica do sistema (em outras palavras, o hamiltoniano pode ser dividido na soma dos termos orbitais e de spin). A dependência do tempo pode ser colocada em qualquer fator, e a evolução do tempo de cada um pode ser estudada separadamente. A fatoração não é possível para aquelas interações onde um campo externo ou qualquer quantidade dependente do espaço acopla ao spin; exemplos incluem uma partícula em um campo magnético e acoplamento spin-órbita .

A discussão anterior não se limita ao spin como uma variável discreta, o momento angular total J também pode ser usado. Outros graus discretos de liberdade, como isospin , podem ser expressos de forma semelhante ao caso do spin acima.

Estados de muitas partículas no espaço de posição 3d

Ondas viajantes de duas partículas livres, com duas de três dimensões suprimidas. O topo é a função de onda do espaço de posição, o fundo é a função de onda do espaço de momento, com densidades de probabilidade correspondentes.

Se houver muitas partículas, em geral haverá apenas uma função de onda, não uma função de onda separada para cada partícula. O fato de uma função de onda descrever muitas partículas é o que torna possível o emaranhamento quântico e o paradoxo EPR . A função de onda de espaço de posição para $N$ partículas é escrita:

{\ displaystyle \ Psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2} \ cdots \ mathbf {r} _ {N}, t)}

onde $r i$ é a posição da $i$ ésima partícula no espaço tridimensional e $t$ é o tempo. Ao todo, esta é uma função de valor complexo de $3 N + 1$ variáveis reais.

Na mecânica quântica, há uma distinção fundamental entre partículas idênticas e partículas distinguíveis . Por exemplo, quaisquer dois elétrons são idênticos e fundamentalmente indistinguíveis um do outro; as leis da física tornam impossível "carimbar um número de identificação" em um determinado elétron para rastreá-lo. Isso se traduz em um requisito da função de onda para um sistema de partículas idênticas:

{\ displaystyle \ Psi \ left (\ ldots \ mathbf {r} _ {a}, \ ldots, \ mathbf {r} _ {b}, \ ldots \ right) = \ pm \ Psi \ left (\ ldots \ mathbf {r} _ {b}, \ ldots, \ mathbf {r} _ {a}, \ ldots \ right)}

onde o sinal $+$ ocorre se as partículas são todas bósons e o sinal $-$ se são todas férmions . Em outras palavras, a função de onda ou é totalmente simétrica nas posições dos bósons, ou totalmente antissimétrica nas posições dos férmions. O intercâmbio físico de partículas corresponde a alternar matematicamente os argumentos na função de onda. O recurso de antissimetria das funções de onda fermiônica leva ao princípio de Pauli . Geralmente, os requisitos de simetria bosônica e fermiônica são a manifestação da estatística de partículas e estão presentes em outros formalismos de estado quântico.

Para $N$ partículas distinguíveis (nenhum dois sendo idêntico , ou seja, nenhum dois tendo o mesmo conjunto de números quânticos), não há nenhum requisito para a função de onda ser simétrica ou anti-simétrica.

Para uma coleção de partículas, algumas idênticas às coordenadas $r 1, r 2, ...$ e outras distinguíveis $x 1, x 2, ...$ (não idênticas entre si, e não idênticas às partículas idênticas mencionadas acima), a onda a função é simétrica ou antissimétrica nas coordenadas de partícula idênticas $r i$ apenas:

{\ displaystyle \ Psi \ left (\ ldots \ mathbf {r} _ {a}, \ ldots, \ mathbf {r} _ {b}, \ ldots, \ mathbf {x} _ {1}, \ mathbf {x } _ {2}, \ ldots \ right) = \ pm \ Psi \ left (\ ldots \ mathbf {r} _ {b}, \ ldots, \ mathbf {r} _ {a}, \ ldots, \ mathbf { x} _ {1}, \ mathbf {x} _ {2}, \ ldots \ right)}

Novamente, não há requisito de simetria para as coordenadas de partícula distinguíveis $x i$ .

A função de onda para N partículas, cada uma com spin é a função de valor complexo

{\ displaystyle \ Psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1}, s_ {z \, 2} \ cdots s_ {z \, N}, t)}

Acumular todos esses componentes em um único vetor,

{\ displaystyle \ underbrace {| \ Psi \ rangle} _ {\ text {vetor de estado (ket)}} = \ underbrace {\ overbrace {\ sum _ {s_ {z \, 1}, \ ldots, s_ {z \ , N}}} ^ {\ text {etiquetas discretas}} \ overbrace {\ int \ limits \ limits _ {R_ {N}} d ^ {3} \ mathbf {r} _ {N} \ cdots \ int \ limits \ limits _ {R_ {1}} d ^ {3} \ mathbf {r} _ {1}} ^ {\ text {rótulos contínuos}}} _ {\ text {somando}} \, \ underbrace {{\ Psi} (\ mathbf {r} _ {1}, \ ldots, \ mathbf {r} _ {N}, s_ {z \, 1}, \ ldots, s_ {z \, N})} _ {\ text {função de onda (componente do vetor de estado ao longo do estado de base)}} \ underbrace {| \ mathbf {r} _ {1}, \ ldots, \ mathbf {r} _ {N}, s_ {z \, 1}, \ ldots, s_ {z \, N} \ rangle} _ {\ text {estado de base (ket de base)}} \ ,.}

Para partículas idênticas, os requisitos de simetria se aplicam aos argumentos de posição e spin da função de onda para que tenha a simetria correta geral.

As fórmulas para os produtos internos são integrais sobre todas as coordenadas ou momentos e somas sobre todos os números quânticos de spin. Para o caso geral de $N$ partículas com spin em 3d,

{\ displaystyle (\ Psi _ {1}, \ Psi _ {2}) = \ sum _ {s_ {z \, N}} \ cdots \ sum _ {s_ {z \, 2}} \ sum _ {s_ {z \, 1}} \ int \ limits _ {\ mathrm {todos \, espaço}} d ^ {3} \ mathbf {r} _ {1} \ int \ limits _ {\ mathrm {todos \, espaço} } d ^ {3} \ mathbf {r} _ {2} \ cdots \ int \ limits _ {\ mathrm {todos \, espaço}} d ^ {3} \ mathbf {r} _ {N} \ Psi _ { 1} ^ {*} \ left (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ right ) \ Psi _ {2} \ left (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ direito)}

isto é, ao todo, $N$ integrais tridimensionais de volume e $N$ somas sobre os spins. Os elementos de volume diferencial $d 3 r i$ também são escritos " $dV i$ " ou " $dx i dy i dz i$ ".

As transformadas de Fourier multidimensionais das funções de onda espacial de rotação de posição ou posição geram funções de onda espacial de rotação momentum ou momentum.

Interpretação de probabilidade

Para o caso geral de $N$ partículas com spin em 3d, se $Ψ$ for interpretado como uma amplitude de probabilidade, a densidade de probabilidade é

{\ displaystyle \ rho \ left (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ right) = \ left | \ Psi \ left (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, s_ {z \, 1} \ cdots s_ {z \, N}, t \ right ) \ right | ^ {2}}

e a probabilidade de que a partícula 1 está na região $R 1$ com spin $s z 1 = m 1$ e a partícula 2 está na região $R 2$ com spin $s z 2 = m 2$ etc. no tempo $t$ é a integral da densidade de probabilidade sobre essas regiões e avaliados nestes números de spin:

{\ displaystyle P _ {\ mathbf {r} _ {1} \ in R_ {1}, s_ {z \, 1} = m_ {1}, \ ldots, \ mathbf {r} _ {N} \ in R_ { N}, s_ {z \, N} = m_ {N}} (t) = \ int \ limits _ {R_ {1}} d ^ {3} \ mathbf {r} _ {1} \ int \ limits _ {R_ {2}} d ^ {3} \ mathbf {r} _ {2} \ cdots \ int \ limits _ {R_ {N}} d ^ {3} \ mathbf {r} _ {N} \ left | \ Psi \ left (\ mathbf {r} _ {1} \ cdots \ mathbf {r} _ {N}, m_ {1} \ cdots m_ {N}, t \ right) \ right | ^ {2}}

Dependência do tempo

Para sistemas em potenciais independentes do tempo, a função de onda pode sempre ser escrita como uma função dos graus de liberdade multiplicados por um fator de fase dependente do tempo, cuja forma é dada pela equação de Schrödinger. Para $N$ partículas, considerando apenas suas posições e suprimindo outros graus de liberdade,

{\ displaystyle \ Psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2}, \ ldots, \ mathbf {r} _ {N}, t) = e ^ {- iEt / \ hbar } \, \ psi (\ mathbf {r} _ {1}, \ mathbf {r} _ {2}, \ ldots, \ mathbf {r} _ {N}) \ ,,}

onde $E$ é o autovalor de energia do sistema correspondente ao autopromoção $Ψ$ . As funções de onda desta forma são chamadas de estados estacionários .

A dependência do tempo do estado quântico e dos operadores pode ser colocada de acordo com transformações unitárias nos operadores e estados. Para qualquer estado quântico $| Ψ⟩$ e operador $O$ , na imagem de Schrödinger $| Ψ (t)⟩$ muda com o tempo de acordo com a equação de Schrödinger enquanto $O$ é constante. Na imagem de Heisenberg ocorre o contrário, $| Ψ⟩$ é constante enquanto $O (t)$ evolui com o tempo de acordo com a equação de movimento de Heisenberg. A imagem de Dirac (ou interação) é intermediária, a dependência do tempo ocorre tanto nos operadores quanto nos estados que evoluem de acordo com as equações de movimento. É útil principalmente em computação elementos S-matriz .

Exemplos não relativísticos

A seguir estão as soluções para a equação de Schrödinger para uma partícula sem spin não relativística.

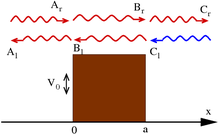
Barreira de potencial finito

Espalhamento em uma barreira de potencial finito de altura

V 0

. As amplitudes e a direção das ondas em movimento à esquerda e à direita são indicadas. Em vermelho, aquelas ondas utilizadas para a derivação da amplitude de reflexão e transmissão.

E > V 0

para esta ilustração.

Uma das características mais proeminentes da mecânica ondulatória é a possibilidade de uma partícula atingir um local com um potencial de força proibitivo (na mecânica clássica) . Um modelo comum é a " barreira potencial ", o caso unidimensional tem o potencial

{\ displaystyle V (x) = {\ begin {cases} V_ {0} & | x | <a \\ 0 & | x | \ geq a \ end {cases}}}

e as soluções de estado estacionário para a equação de onda têm a forma (para algumas constantes $k, κ$ )

{\ displaystyle \ Psi (x) = {\ begin {cases} A _ {\ mathrm {r}} e ^ {ikx} + A _ {\ mathrm {l}} e ^ {- ikx} & x <-a, \\ B _ {\ mathrm {r}} e ^ {\ kappa x} + B _ {\ mathrm {l}} e ^ {- \ kappa x} & | x | \ leq a, \\ C _ {\ mathrm {r}} e ^ {ikx} + C _ {\ mathrm {l}} e ^ {- ikx} & x> a. \ end {casos}}}

Observe que essas funções de onda não são normalizadas; veja a teoria de espalhamento para discussão.

A interpretação padrão disso é como um fluxo de partículas sendo disparado na etapa da esquerda (a direção de $x$ negativo ): definir $A r = 1$ corresponde a partículas disparadas individualmente; os termos contendo $A r$ e $C r$ significam movimento para a direita, enquanto $A l$ e $C l$ - para a esquerda. Sob esta interpretação do feixe, coloque $C l = 0,$ uma vez que nenhuma partícula está vindo da direita. Aplicando a continuidade das funções de onda e suas derivadas nos limites, é possível determinar as constantes acima.

Funções de onda de elétrons confinados 3D em um ponto quântico. Aqui, pontos quânticos retangulares e triangulares são mostrados. Estados de energia em pontos retangulares são mais s do tipo e do tipo p . No entanto, em um ponto triangular, as funções de onda são misturadas devido à simetria de confinamento. (Clique para ver a animação)

Em um cristalito semicondutor cujo raio é menor que o tamanho do raio de Bohr do exciton , os excitons são comprimidos, levando ao confinamento quântico . Os níveis de energia podem então ser modelados usando a partícula em um modelo de caixa em que a energia de diferentes estados depende do comprimento da caixa.

Oscilador harmônico quântico

As funções de onda para o oscilador harmônico quântico podem ser expressas em termos de polinômios de Hermite $H n$ , eles são

{\ displaystyle \ Psi _ {n} (x) = {\ sqrt {\ frac {1} {2 ^ {n} \, n!}}} \ cdot \ left ({\ frac {m \ omega} {\ pi \ hbar}} \ right) ^ {1/4} \ cdot e ^ {- {\ frac {m \ omega x ^ {2}} {2 \ hbar}}} \ cdot H_ {n} \ left ({ \ sqrt {\ frac {m \ omega} {\ hbar}}} x \ right)}

onde $n = 0, 1, 2,\dots$ .

A densidade de probabilidade do elétron para os primeiros orbitais de elétrons do átomo de hidrogênio mostrado como seções transversais. Esses orbitais formam uma base ortonormal para a função de onda do elétron. Orbitais diferentes são representados em escalas diferentes.

Átomo de hidrogênio

As funções de onda de um elétron em um átomo de hidrogênio são expressas em termos de harmônicos esféricos e polinômios de Laguerre generalizados (estes são definidos de forma diferente por diferentes autores - veja o artigo principal sobre eles e o átomo de hidrogênio).

É conveniente usar coordenadas esféricas, e a função de onda pode ser separada em funções de cada coordenada,

{\ displaystyle \ Psi _ {n \ ell m} (r, \ theta, \ phi) = R (r) \, \, Y _ {\ ell} ^ {m} \! (\ theta, \ phi)}

onde $R$ são funções radiais e $Y m ℓ (θ, φ)$ são harmônicos esféricos de grau $ℓ$ e ordem $m$ . Este é o único átomo para o qual a equação de Schrödinger foi resolvida com exatidão. Os átomos multielétrons requerem métodos aproximados. A família de soluções é:

{\ displaystyle \ Psi _ {n \ ell m} (r, \ theta, \ phi) = {\ sqrt {{\ left ({\ frac {2} {na_ {0}}} \ right)} ^ {3 } {\ frac {(n- \ ell -1)!} {2n [(n + \ ell)!]}}}} e ^ {- r / na_ {0}} \ left ({\ frac {2r} { na_ {0}}} \ right) ^ {\ ell} L_ {n- \ ell -1} ^ {2 \ ell +1} \ left ({\ frac {2r} {na_ {0}}} \ right) \ cdot Y _ {\ ell} ^ {m} (\ theta, \ phi)}

onde $um 0 = 4 πε 0 ħ 2 / m de e e 2$ é o de Bohr raio , $L 2 ℓ + 1 n - ℓ - 1$ são os polinômios de Laguerre generalizados de grau $n - ℓ - 1$ , $n = 1, 2, ...$ é o número quântico principal , $ℓ = 0, 1, ... n - 1$ o número quântico azimutal , $m = - ℓ, - ℓ + 1, ..., ℓ - 1, ℓ$ o número quântico magnético . Átomos semelhantes ao hidrogênio têm soluções muito semelhantes.

Esta solução não leva em consideração o spin do elétron.

Na figura dos orbitais de hidrogênio, as 19 subimagens são imagens de funções de onda no espaço de posição (sua norma ao quadrado). As funções de onda representam o estado abstrato caracterizado pelo triplo dos números quânticos $(n, l, m)$ , no canto inferior direito de cada imagem. Estes são o número quântico principal, o número quântico do momento angular orbital e o número quântico magnético. Junto com um número quântico de projeção de spin do elétron, este é um conjunto completo de observáveis.

A figura pode servir para ilustrar algumas propriedades adicionais dos espaços de funções das funções de onda.

Neste caso, as funções de onda são quadradas integráveis. Pode-se inicialmente tomar o espaço de funções como o espaço de funções quadradas integráveis, geralmente denotadas por $L 2$ .
As funções exibidas são soluções para a equação de Schrödinger. Obviamente, nem todas as funções em $L 2$ satisfazem a equação de Schrödinger para o átomo de hidrogênio. O espaço de função é, portanto, um subespaço de $L 2$ .
As funções exibidas fazem parte de uma base para o espaço funcional. A cada triplo $(n, l, m)$ , corresponde uma função de onda básica. Se o spin for levado em consideração, existem duas funções básicas para cada triplo. O espaço funcional, portanto, tem uma base contável .
As funções básicas são mutuamente ortonormais .

Funções de onda e espaços funcionais

O conceito de espaços de funções entra naturalmente na discussão sobre funções de onda. Um espaço de funções é um conjunto de funções, geralmente com alguns requisitos de definição nas funções (no caso presente, eles são integráveis em forma de quadrado ), às vezes com uma estrutura algébrica no conjunto (no caso presente uma estrutura de espaço vetorial com um produto interno ), junto com uma topologia no conjunto. O último será usado esparsamente aqui, ele só é necessário para obter uma definição precisa do que significa um subconjunto de um espaço de função ser fechado . Concluiremos a seguir que o espaço funcional das funções de onda é um espaço de Hilbert . Essa observação é a base da formulação matemática predominante da mecânica quântica.

Estrutura do espaço vetorial

Uma função de onda é um elemento de um espaço funcional parcialmente caracterizado pelas seguintes descrições concretas e abstratas.

A equação de Schrödinger é linear. Isso significa que as soluções para ele, funções de onda, podem ser adicionadas e multiplicadas por escalares para formar uma nova solução. O conjunto de soluções para a equação de Schrödinger é um espaço vetorial.
O princípio da superposição da mecânica quântica. Se $Ψ$ e $Φ$ são dois estados no espaço abstrato de estados de um sistema mecânico quântico, e $um$ e $b$ são dois números complexos, então $um Ψ + b Φ$ é um estado válido também. (Se os nula vetor conta como um estado válido ( "nenhum sistema de presente") é uma questão de definição. O vector nulo se não a qualquer taxa de descrever o estado de vácuo na teoria quântica de campos.) O conjunto de estados permitidos é um espaço vetorial .

Obviamente, essa semelhança não é acidental. Também há uma distinção entre os espaços a ter em mente.

Representações

Os estados básicos são caracterizados por um conjunto de números quânticos. Este é um conjunto de autovalores de um conjunto máximo de observáveis de comutação . Os observáveis físicos são representados por operadores lineares, também chamados de observáveis, no espaço de vetores. Maximalidade significa que não pode ser adicionado ao conjunto nenhum outro observável algebricamente independente que comute com os já presentes. A escolha de tal conjunto pode ser chamada de escolha de representação .

É um postulado da mecânica quântica que uma quantidade fisicamente observável de um sistema, como posição, momento ou spin, é representada por um operador Hermitiano linear no espaço de estados. Os resultados possíveis da medição da quantidade são os autovalores do operador. Em um nível mais profundo, a maioria dos observáveis, talvez todos, surgem como geradores de simetrias .
A interpretação física é que tal conjunto representa o que pode - em teoria - ser medido simultaneamente com precisão arbitrária. A relação de incerteza de Heisenberg proíbe medições exatas simultâneas de dois observáveis não comutantes.
O conjunto não é único. Pode ser, para um sistema de uma partícula, por exemplo, projeção de posição e spin $z$ , $(x, S z)$ , ou pode ser momentum e projeção de spin $y$ , $(p, S y)$ . Nesse caso, o operador correspondente à posição (um operador de multiplicação na representação da posição) e o operador correspondente à quantidade de movimento (um operador diferencial na representação da posição) não comutam.
Uma vez que uma representação é escolhida, ainda há arbitrariedade. Resta escolher um sistema de coordenadas. Isso pode, por exemplo, corresponder a uma escolha de eixos $x, y$ e $z$ , ou uma escolha de coordenadas curvilíneas, conforme exemplificado pelas coordenadas esféricas usadas para as funções de onda atômica de hidrogênio. Essa escolha final também fixa uma base no espaço abstrato de Hilbert. Os estados básicos são rotulados pelos números quânticos correspondentes ao conjunto máximo de observáveis de comutação e um sistema de coordenadas apropriado.

Os estados abstratos são "abstratos" apenas no sentido de que uma escolha arbitrária necessária para uma descrição explícita particular dele não é fornecida. Isso é o mesmo que dizer que nenhuma escolha de conjunto máximo de observáveis de comutação foi dada. Isso é análogo a um espaço vetorial sem uma base especificada. As funções de onda correspondentes a um estado, portanto, não são exclusivas. Essa não-unicidade reflete a não-unicidade na escolha de um conjunto máximo de observáveis de comutação. Para uma partícula de spin em uma dimensão, a um estado particular corresponde duas funções de onda, $Ψ (x, S z)$ e $Ψ (p, S y)$ , ambas descrevendo o mesmo estado.

Para cada escolha de conjuntos de observáveis comutáveis máximos para o espaço de estado abstrato, existe uma representação correspondente que está associada a um espaço de funções de funções de onda.
Entre todos esses diferentes espaços de função e o espaço de estado abstrato, há correspondências um-para-um (aqui desconsiderando a normalização e os fatores de fase não observáveis), sendo o denominador comum um estado abstrato particular. A relação entre as funções de onda espacial de momento e posição, por exemplo, descrevendo o mesmo estado é a transformada de Fourier .

Cada escolha de representação deve ser pensada como especificando um espaço de função único no qual vivem as funções de onda correspondentes a essa escolha de representação. Essa distinção é melhor mantida, mesmo se alguém pudesse argumentar que dois desses espaços de função são matematicamente iguais, por exemplo, sendo o conjunto de funções quadradas integráveis. Pode-se então pensar nos espaços de função como duas cópias distintas desse conjunto.

Produto Interno

Há uma estrutura algébrica adicional nos espaços vetoriais das funções de onda e no espaço de estado abstrato.

Fisicamente, diferentes funções de onda são interpretadas como sobrepostas em algum grau. Um sistema em um estado $Ψ$ que não se sobrepõe a um estado $Φ$ não pode ser encontrado no estado $Φ$ após a medição. Mas se $Φ 1, Φ 2,\dots se$ sobrepõem a $Ψ$ em algum grau, há uma chance de que a medição de um sistema descrito por $Ψ$ seja encontrada nos estados $Φ 1, Φ 2,\dots$ . Também se aplicam as regras de seleção . Geralmente são formulados na preservação de alguns números quânticos. Isso significa que certos processos permitidos de algumas perspectivas (por exemplo, conservação de energia e momento) não ocorrem porque as funções de onda total inicial e final não se sobrepõem.
Matematicamente, verifica-se que as soluções para a equação de Schrödinger para potenciais particulares são ortogonais de alguma maneira, isso geralmente é descrito por uma integral

{\ displaystyle \ int \ Psi _ {m} ^ {*} \ Psi _ {n} w \, dV = \ delta _ {nm},}

onde

m, n

são (conjuntos de) índices (números quânticos) que rotulam soluções diferentes, a função estritamente positiva

w

é chamada de função de peso e

δ mn

é o delta de Kronecker . A integração é realizada em todo o espaço relevante.

Isso motiva a introdução de um produto interno no espaço vetorial de estados quânticos abstratos, compatível com as observações matemáticas acima ao passar para uma representação. É denotado $(Ψ, Φ)$ , ou na notação Bra – ket $⟨Ψ | Φ⟩$ . Isso produz um número complexo. Com o produto interno, o espaço funcional é um espaço interno do produto . A aparência explícita do produto interno (geralmente um integral ou uma soma de integrais) depende da escolha da representação, mas o número complexo $(Ψ, Φ)$ não. Muito da interpretação física da mecânica quântica deriva da regra de Born . Afirma que a probabilidade $p$ de encontrar na medição o estado $Φ$ dado que o sistema está no estado $Ψ$ é

{\ displaystyle p = | (\ Phi, \ Psi) | ^ {2},}

onde $Φ$ e $Ψ$ são considerados normalizados. Considere um experimento de espalhamento . Na teoria quântica de campos, se $Φ out$ descreve um estado no "futuro distante" (um "estado externo") depois que as interações entre as partículas de dispersão cessaram, e $Ψ em$ um "estado" no "passado distante", então as quantidades $(Φ out, Ψ in)$ , com $Φ out$ e $Ψ in$ variando sobre um conjunto completo de estados in e out respectivamente, é chamada de matriz S ou matriz de dispersão . O conhecimento dele é, efetivamente, ter resolvido a teoria em questão, pelo menos no que diz respeito às previsões. Quantidades mensuráveis, como taxas de decaimento e seções transversais de espalhamento, podem ser calculadas a partir da matriz-S.

Espaço Hilbert

As observações acima encapsulam a essência dos espaços de funções dos quais as funções de onda são elementos. No entanto, a descrição ainda não está completa. Há um outro requisito técnico sobre o espaço de funções, o de completude , que permite tomar limites de sequências no espaço de funções e garantir que, se o limite existir, é um elemento do espaço de funções. Um espaço de produto interno completo é chamado de espaço de Hilbert . A propriedade de completude é crucial em tratamentos e aplicações avançadas da mecânica quântica. Por exemplo, a existência de operadores de projeção ou projeções ortogonais depende da integridade do espaço. Esses operadores de projeção, por sua vez, são essenciais para a declaração e prova de muitos teoremas úteis, por exemplo, o teorema espectral . Não é muito importante na introdução à mecânica quântica, e detalhes técnicos e links podem ser encontrados em notas de rodapé como a que segue. O espaço $L 2$ é um espaço de Hilbert, com produto interno apresentado posteriormente. O espaço funcional do exemplo da figura é um subespaço de $L 2$ . Um subespaço de um espaço de Hilbert é um espaço de Hilbert se estiver fechado.

Em resumo, o conjunto de todas as funções de onda normalizáveis possíveis para um sistema com uma escolha particular de base, juntamente com o vetor nulo, constituem um espaço de Hilbert.

Nem todas as funções de interesse são elementos de algum espaço de Hilbert, digamos $L 2$ . O exemplo mais evidente é o conjunto de funções $e 2 πi p \cdot x ⁄ h$ . Estas são soluções de ondas planas da equação de Schrödinger para uma partícula livre, mas não são normalizáveis, portanto, não em $L 2$ . Mas não deixam de ser fundamentais para a descrição. Pode-se, usando-os, expressar funções que são normalizáveis usando pacotes de ondas . Eles são, em certo sentido, uma base (mas não uma base espacial de Hilbert, nem uma base de Hamel ) na qual as funções de onda de interesse podem ser expressas. Há também o artefato "normalização para uma função delta" que é freqüentemente empregado por conveniência de notação, veja mais adiante. As funções delta em si também não são quadradas integráveis.

A descrição acima do espaço de função que contém as funções de onda é principalmente motivada matematicamente. Os espaços funcionais são, devido à completude, muito grandes em certo sentido. Nem todas as funções são descrições realistas de qualquer sistema físico. Por exemplo, no espaço funcional $L 2$ pode-se encontrar a função que assume o valor $0$ para todos os números racionais e $- i$ para os irracionais no intervalo $[0, 1]$ . Este é quadrado integrável, mas dificilmente pode representar um estado físico.

Espaços de Hilbert comuns

Embora o espaço de soluções como um todo seja um espaço de Hilbert, existem muitos outros espaços de Hilbert que normalmente ocorrem como ingredientes.

Funções avaliadas complexas integráveis quadradas no intervalo $[0, 2 π]$ . O conjunto ${e int / 2 π, n \in ℤ}$ é uma base do espaço de Hilbert, ou seja, um conjunto ortonormal máximo.
A transformada de Fourier assume funções no espaço acima para elementos de $l 2 (ℤ)$ , o espaço de funções $somadoras$ quadradas $ℤ \to ℂ$ . O último espaço é um espaço de Hilbert e a transformada de Fourier é um isomorfismo dos espaços de Hilbert. Sua base é ${e i, i \in ℤ}$ com $e i (j) = δ ij, i, j \in ℤ$ .
O exemplo mais básico de polinômios abrangentes está no espaço de funções quadradas integráveis no intervalo $[-1, 1]$ para o qual os polinômios de Legendre são uma base espacial de Hilbert (conjunto ortonormal completo).
As funções quadradas integráveis na esfera unitária $S 2$ é um espaço de Hilbert. As funções básicas neste caso são os harmônicos esféricos . Os polinômios de Legendre são ingredientes dos harmônicos esféricos. A maioria dos problemas com simetria rotacional terá "a mesma" solução (conhecida) com respeito a essa simetria, de modo que o problema original é reduzido a um problema de dimensionalidade inferior.
Os polinômios de Laguerre associados aparecem no problema da função de onda hidrogenica após fatorar os harmônicos esféricos. Estes abrangem o espaço de Hilbert de funções quadradas integráveis no intervalo semi-infinito $[0, \infty)$ .

De forma mais geral, pode-se considerar um tratamento unificado de todas as soluções polinomiais de segunda ordem para as equações de Sturm-Liouville na configuração do espaço de Hilbert. Isso inclui os polinômios de Legendre e Laguerre, bem como polinômios de Chebyshev , polinômios de Jacobi e polinômios de Hermite . Todos esses realmente aparecem em problemas físicos, os últimos no oscilador harmônico , e o que de outra forma seria um labirinto desconcertante de propriedades de funções especiais torna-se um corpo organizado de fatos. Para isso, consulte Byron & Fuller (1992 , Capítulo 5).

Também ocorrem espaços de Hilbert de dimensão finita. O espaço $ℂ n$ é um espaço de Hilbert de dimensão $n$ . O produto interno é o produto interno padrão nesses espaços. Nele reside a "parte do spin" de uma única função de onda de partícula.

Na descrição não relativística de um elétron, tem-se $n = 2$ e a função de onda total é uma solução da equação de Pauli .
No tratamento relativístico correspondente, $n = 4$ e a função de onda resolve a equação de Dirac .

Com mais partículas, as situações são mais complicadas. É preciso empregar produtos tensores e usar a teoria de representação dos grupos de simetria envolvidos (o grupo de rotação e o grupo de Lorentz respectivamente) para extrair do produto tensorial os espaços nos quais residem as funções de onda de spin (total). (Problemas adicionais surgem no caso relativístico, a menos que as partículas estejam livres. Veja a equação de Bethe-Salpeter .) Observações correspondentes se aplicam ao conceito de isospin , para o qual o grupo de simetria é SU (2) . Os modelos das forças nucleares dos anos 60 (ainda úteis hoje, ver força nuclear ) usavam o grupo de simetria SU (3) . Nesse caso, também, a parte das funções de onda correspondentes às simetrias internas residem em alguns $ℂ n$ ou subespaços de produtos tensores de tais espaços.

Na teoria quântica de campos, o espaço de Hilbert subjacente é o espaço de Fock . É construído a partir de estados de partícula única livres, ou seja, funções de onda quando uma representação é escolhida, e pode acomodar qualquer número de partículas finito, não necessariamente constante no tempo. A dinâmica interessante (ou melhor, tratável ) reside não nas funções de onda, mas nos operadores de campo que são operadores atuando no espaço Fock. Assim, a imagem de Heisenberg é a escolha mais comum (estados constantes, operadores que variam no tempo).

Devido à natureza infinita dimensional do sistema, as ferramentas matemáticas apropriadas são objetos de estudo na análise funcional .

Descrição simplificada

Continuidade da função de onda e sua primeira derivada espacial (na direção x , coordenadas y e z não mostradas), em algum momento t .

Nem todos os livros didáticos introdutórios seguem o longo caminho e apresentam a maquinaria espacial de Hilbert completa, mas o foco está na equação de Schrödinger não relativística na representação de posição para certos potenciais padrão. As seguintes restrições na função de onda às vezes são formuladas explicitamente para que os cálculos e a interpretação física façam sentido:

A função de onda deve ser quadrada integrável . Isso é motivado pela interpretação de Copenhagen da função de onda como uma amplitude de probabilidade.
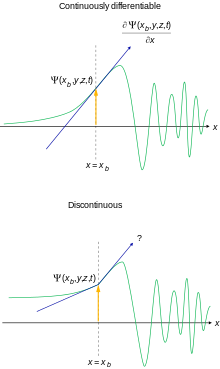
Deve ser contínuo em todos os lugares e continuamente diferenciável em todos os lugares . Isso é motivado pelo aparecimento da equação de Schrödinger para a maioria dos potenciais fisicamente razoáveis.

É possível relaxar um pouco essas condições para fins especiais. Se esses requisitos não forem atendidos, não será possível interpretar a função de onda como uma amplitude de probabilidade.

Isso não altera a estrutura do espaço de Hilbert que essas funções de onda particulares habitam, mas o subespaço das funções quadradas integráveis $L 2$ , que é um espaço de Hilbert, satisfazendo o segundo requisito não é fechado em $L 2$ , portanto, não é um espaço de Hilbert espaço em si. As funções que não atendem aos requisitos ainda são necessárias por razões técnicas e práticas.

Mais sobre funções de onda e espaço de estado abstrato

Como foi demonstrado, o conjunto de todas as funções de onda possíveis em alguma representação de um sistema constitui um espaço de Hilbert de dimensão infinita em geral . Devido às múltiplas escolhas possíveis de base de representação, esses espaços de Hilbert não são únicos. Fala-se, portanto, de um espaço de Hilbert abstrato, espaço de estado , onde a escolha da representação e da base é deixada indeterminada. Especificamente, cada estado é representado como um vetor abstrato no espaço de estados. Um estado quântico $| Ψ⟩$ em qualquer representação é geralmente expresso como um vetor

{\ displaystyle | \ Psi \ rangle = \ sum _ {\ boldsymbol {\ alpha}} \ int d ^ {m} \! {\ boldsymbol {\ omega}} \, \, \ Psi ({\ boldsymbol {\ alpha }}, {\ boldsymbol {\ omega}}, t) \, | {\ boldsymbol {\ alpha}}, {\ boldsymbol {\ omega}} \ rangle}

Onde

$| α, co ⟩$ os vectores de base da representação escolhida
$d m ω = dω 1 dω 2 ... dω m$ um " elemento de volume diferencial " em graus de liberdade contínuos
$Ψ (α, ω, t)$ uma componente do vetor $| Ψ⟩$ , chamada de função de onda do sistema
$α = (α 1, α 2, ..., α n)$ números quânticos discretos adimensionais
$ω = (ω 1, ω 2, ..., ω m)$ variáveis contínuas (não necessariamente adimensionais)

Esses números quânticos indexam os componentes do vetor de estado. $Além disso$ , todos os $α$ estão em um conjunto $n-$ dimensional $A$ $=$ $A$ $1$ $\times$ $A$ $2$ $\times ...$ $A$ $n$ onde cada $A$ $i$ é o conjunto de valores permitidos para $α$ $i$ ; todos os $ω$ estão em um "volume" $m-$ dimensional $Ω \subseteq ℝ$ $m$ onde $Ω = Ω$ $1$ $\times Ω$ $2$ $\times ... Ω$ $m$ e cada $Ω$ $i$ $\subseteq ℝ$ é o conjunto de valores permitidos para $ω$ $i$ , um subconjunto do real números $ℝ$ . Para generalidade, $n$ e $m$ não são necessariamente iguais.

Exemplo:

(a) Para uma única partícula em 3d com spin s , negligenciando outros graus de liberdade, usando coordenadas cartesianas, poderíamos tomar $α = (s z)$ para o número quântico de spin da partícula ao longo da direção z, e $ω = (x, y, z)$ para as coordenadas de posição da partícula. Aqui, $A = {- s, - s + 1, ..., s - 1, s}$ é o conjunto de números quânticos de spin permitidos e $Ω = ℝ 3$ é o conjunto de todas as posições de partícula possíveis em todo o espaço de posição 3d.

(b) Uma escolha alternativa é $α = (s y)$ para o número quântico de spin ao longo da direção y e $ω = (p x, p y, p z)$ para os componentes do momento da partícula. Neste caso, $A$ e $Ω$ são os mesmos de antes.

A densidade de probabilidade de encontrar o sistema no momento no estado $|$ $α$ $,$ $co$ $⟩$ seja ${\ displaystyle t}$

{\ displaystyle \ rho _ {\ alpha, \ omega} (t) = | \ Psi ({\ boldsymbol {\ alpha}}, {\ boldsymbol {\ omega}}, t) | ^ {2}}

A probabilidade de encontrar o sistema com $α$ em algumas ou todas as configurações de variáveis discretas possíveis, $D \subseteq A$ , e $ω$ em algumas ou todas as configurações de variáveis contínuas possíveis, $C \subseteq Ω$ , é a soma e integral sobre a densidade,

{\ displaystyle P (t) = \ sum _ {{\ boldsymbol {\ alpha}} \ in D} \ int _ {C} \ rho _ {\ alpha, \ omega} (t) \, \, d ^ { m} \! {\ boldsymbol {\ omega}}}

Uma vez que a soma de todas as probabilidades deve ser 1, a condição de normalização

{\ displaystyle 1 = \ sum _ {{\ boldsymbol {\ alpha}} \ in A} \ int _ {\ Omega} \ rho _ {\ alpha, \ omega} (t) \, \, d ^ {m} \! {\ boldsymbol {\ omega}}}

deve ser mantida em todos os momentos durante a evolução do sistema.

A condição de normalização requer que $ρ d m ω$ seja adimensional, por análise dimensional $Ψ$ deve ter as mesmas unidades que $(ω 1 ω 2 ... ω m) -1/2$ .

Ontologia

Se a função de onda realmente existe, e o que ela representa, são questões importantes na interpretação da mecânica quântica . Muitos físicos famosos de uma geração anterior ficaram intrigados com esse problema, como Schrödinger , Einstein e Bohr . Alguns defendem formulações ou variantes da interpretação de Copenhague (por exemplo, Bohr, Wigner e von Neumann ), enquanto outros, como Wheeler ou Jaynes , adotam a abordagem mais clássica e consideram a função de onda como representando informações na mente do observador, ou seja, uma medida do nosso conhecimento da realidade. Alguns, incluindo Schrödinger, Bohm e Everett e outros, argumentaram que a função de onda deve ter uma existência física objetiva. Einstein pensava que uma descrição completa da realidade física deveria se referir diretamente ao espaço físico e ao tempo, diferentemente da função de onda, que se refere a um espaço matemático abstrato.

Veja também

Observações

Citações

Fontes gerais

Arons, AB; Peppard, MB (1965). "Proposta de Einstein do conceito de fóton: Uma tradução do artigo Annalen der Physik de 1905" (PDF) . American Journal of Physics . 33 (5): 367. bibcode : 1965AmJPh..33..367A . doi : 10.1119 / 1.1971542 .
Atkins, PW (1974). Quanta: um manual de conceitos . ISBN 978-0-19-855494-3.
Bohr, N. (1985). Kalckar, J. (ed.). Niels Bohr - Collected Works: Foundations of Quantum Physics I (1926 - 1932) . Volume 6. Amsterdam: North Holland. ISBN 978-044453289-3. |volume=tem texto extra ( ajuda )
Born, M. (1926a). "Zur Quantenmechanik der Stoßvorgange". Z. Phys . 37 (12): 863–867. Bibcode : 1926ZPhy ... 37..863B . doi : 10.1007 / bf01397477 . S2CID 119896026 .
Born, M. (1926b). "Quantenmechanik der Stoßvorgange". Z. Phys . 38 (11-12): 803-827. Bibcode : 1926ZPhy ... 38..803B . doi : 10.1007 / bf01397184 . S2CID 126244962 .
Born, M. (1927). "Aspectos físicos da mecânica quântica" . Nature . 119 (2992): 354–357. Bibcode : 1927Natur.119..354B . doi : 10.1038 / 119354a0 .
Born, M. (11 de dezembro de 1954). "A interpretação estatística da mecânica quântica" . Palestra do Nobel . Fundação Nobel . 122 (3172): 675–9. doi : 10.1126 / science.122.3172.675 . PMID 17798674 .
de Broglie, L. (1923). "Radiações - Ondes et quanta" [Radiação - Ondas e quanta]. Comptes Rendus (em francês). 177 : 507–510, 548, 630. Cópia online (francês) Cópia online (inglês)
de Broglie, L. (1960). Mecânica de ondas não lineares: uma interpretação causal . Amsterdam: Elsevier - via Internet Archive .
Byron, FW; Fuller, RW (1992) [Publicado pela primeira vez em 1969]. Matemática da Física Clássica e Quântica . Dover Books on Physics (edição revisada). Publicações de Dover . ISBN 978-0-486-67164-2- via Arquivo da Internet .
Camilleri, K. (2009). Heisenberg e a Interpretação da Mecânica Quântica: o Físico como Filósofo . Cambridge UK: Cambridge University Press. ISBN 978-0-521-88484-6.
Conway, JB (1990). Um Curso de Análise Funcional . Textos de Pós-Graduação em Matemática. Volume 96. Springer Verlag . ISBN 978-0-387-97245-9. |volume=tem texto extra ( ajuda )
Dirac, PAM (1939). "Uma nova notação para a mecânica quântica". Mathematical Proceedings of the Cambridge Philosophical Society . 35 (3): 416–418. Bibcode : 1939PCPS ... 35..416D . doi : 10.1017 / S0305004100021162 .
Dirac, PAM (1982). Os princípios da mecânica quântica . A série internacional de monografias em física (4ª ed.). Imprensa da Universidade de Oxford. ISBN 0-19-852011-5.
Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" . Annalen der Physik (em alemão). 17 (6): 132–148. Bibcode : 1905AnP ... 322..132E . doi : 10.1002 / andp.19053220607 .
Einstein, A. (1916). "Zur Quantentheorie der Strahlung". Mitteilungen der Physikalischen Gesellschaft Zürich . 18 : 47–62.
Einstein, A. (1917). "Zur Quantentheorie der Strahlung". Physikalische Zeitschrift (em alemão). 18 : 121–128. Bibcode : 1917PhyZ ... 18..121E .
Einstein, A. (1998). Schlipp, PA (ed.). Albert Einstein: Filósofo-Cientista . A Biblioteca de Filósofos Vivos. VII (3ª ed.). La Salle Publishing Company, Illinois: Open Court. ISBN 978-0-87548-133-3.
Eisberg, R .; Resnick, R. (1985). Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2ª ed.). John Wiley & Sons. ISBN 978-0-471-87373-0- via Arquivo da Internet .
Greiner, W .; Reinhardt, J. (2008). Quantum Electrodynamics (4ª ed.). springer. ISBN 978-354087560-4.
Griffiths, DJ (2004). Introdução à Mecânica Quântica (2ª ed.). Essex England: Pearson Education. ISBN 978-013111892-8.
Griffiths, David (2008). Introdução às partículas elementares . Wiley-VCH. pp. 162ss. ISBN 978-3-527-40601-2.
ter Haar, D. (1967). A velha teoria quântica . Pergamon Press . pp. 167-183 . LCCN 66029628 - via Internet Archive .
Hanle, PA (1977), "Erwin Schrodinger's Reaction to Louis de Broglie's Thesis on the Quantum Theory", Isis , 68 (4): 606–609, doi : 10.1086 / 351880 , S2CID 121913205
Heisenberg, W. (1958). Física e Filosofia: a Revolução na Ciência Moderna . Nova York: Harper & Row - via Internet Archive .
Jaynes, ET (2003). Larry, G. (ed.). Teoria da probabilidade: a lógica da ciência . Cambridge University Press . ISBN 978-0-521 59271-0.
Landau, LD ; Lifshitz, EM (1977). Mecânica Quântica: Teoria Não Relativística . Vol. 3 (3ª ed.). Pergamon Press . ISBN 978-0-08-020940-1. |volume=tem texto extra ( ajuda ) Cópia online
Lerner, RG ; Trigg, GL (1991). Encyclopaedia of Physics (2ª ed.). Editores VHC. ISBN 978-0-89573-752-6- via Arquivo da Internet .
Ludwig, G. (1968). Mecânica das Ondas . Oxford UK: Pergamon Press. ISBN 978-0-08-203204-5. LCCN 66-30631 - via Internet Archive .
Martin, BR; Shaw, G. (2008). Particle Physics . Manchester Physics Series (3ª ed.). John Wiley & Sons. ISBN 978-0-470-03294-7.
Murdoch, D. (1987). Filosofia da Física de Niels Bohr . Cambridge UK: Cambridge University Press. ISBN 978-0-521-33320-7- via Arquivo da Internet .
Newton, RG (2002). Física Quântica: um Texto para Aluno de Graduação . Nova York: Springer. ISBN 978-0-387-95473-8.
Pauli, Wolfgang (1927). "Zur Quantenmechanik des magnetischen Elektrons". Zeitschrift für Physik (em alemão). 43 (9–10): 601–623. Bibcode : 1927ZPhy ... 43..601P . doi : 10.1007 / bf01397326 . S2CID 128228729 .
Peleg, Y .; Pnini, R .; Zaarur, E .; Hecht, E. (2010). Mecânica quântica . Esboços de Schaum (2ª ed.). McGraw Hill. ISBN 978-0-07-162358-2.
Rae, AIM (2008). Mecânica Quântica . Volume 2 (5ª ed.). Taylor & Francis Group. ISBN 978-1-5848-89700. |volume=tem texto extra ( ajuda )
Schrõdinger, E. (1926). "Uma teoria ondulatória da mecânica dos átomos e moléculas" (PDF) . Revisão física . 28 (6): 1049–1070. Bibcode : 1926PhRv ... 28.1049S . doi : 10.1103 / PhysRev.28.1049 . Arquivado do original (PDF) em 17 de dezembro de 2008.
Shankar, R. (1994). Principles of Quantum Mechanics (2ª ed.). ISBN 978-030644790-7.
Tipler, PA; Mosca, G .; Freeman (2008). Physics for Scientists and Engineers - with Modern Physics (6ª ed.). ISBN 978-0-7167-8964-2.
Weinberg, S. (2002), The Quantum Theory of Fields , 1 , Cambridge University Press, ISBN 978-0-521-55001-7- via Arquivo da Internet
Weinberg, S. (2013), Lectures in Quantum Mechanics , Cambridge University Press, ISBN 978-1-107-02872-2
Wheeler, JA ; Zurek, WH (1983). Teoria e medição quântica . Princeton NJ: Princeton University Press.
Young, HD; Freedman, RA (2008). Pearson (ed.). Sears 'e Zemansky's University Physics (12ª ed.). Addison-Wesley. ISBN 978-0-321-50130-1.
Zettili, N. (2009). Mecânica Quântica: Conceitos e Aplicações (2ª ed.). ISBN 978-0-470-02679-3.
Zwiebach, Barton (2009). Um primeiro curso em teoria das cordas . Cambridge University Press. ISBN 978-0-521-88032-9.

Leitura adicional

Kim, Yong-Ki (2 de setembro de 2000). Física Atômica Prática (PDF) . Instituto Nacional de Padrões e Tecnologia. pp. 1 (55 s). Arquivado do original (PDF) em 22 de julho de 2011.
Polkinghorne, John (2002). Teoria Quântica, uma introdução muito curta . Imprensa da Universidade de Oxford. ISBN 978-0-19-280252-1.

Languages

In other projects