Autômato finito determinístico - Deterministic finite automaton

Um exemplo de autômato finito determinístico que aceita apenas números binários múltiplos de 3. O estado S ₀ é tanto o estado inicial quanto o estado de aceitação. Por exemplo, a string "1001" leva à sequência de estados S ₀ , S ₁ , S ₂ , S ₁ , S ₀ e, portanto, é aceita.

Na teoria da computação , um ramo da ciência da computação teórica , um autômato finito determinístico ( DFA ) - também conhecido como aceitador finito determinístico ( DFA ), máquina de estado finito determinística ( DFSM ) ou autômato de estado finito determinístico ( DFSA ) - é uma máquina de estado finito que aceita ou rejeita uma determinada sequência de símbolos, executando uma sequência de estados determinada exclusivamente pela sequência. Determinístico se refere à exclusividade da execução do cálculo. Em busca dos modelos mais simples para capturar máquinas de estados finitos, Warren McCulloch e Walter Pitts estiveram entre os primeiros pesquisadores a introduzir um conceito semelhante a autômato finito em 1943.

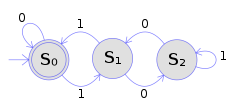
A figura ilustra um autômato finito determinístico usando um diagrama de estado . Neste autômato de exemplo, há três estados: S ₀ , S ₁ e S ₂ (denotados graficamente por círculos). O autômato recebe uma sequência finita de 0s e 1s como entrada. Para cada estado, há uma seta de transição levando a um próximo estado para 0 e 1. Ao ler um símbolo, um DFA salta deterministicamente de um estado para outro seguindo a seta de transição. Por exemplo, se o autômato está atualmente no estado S ₀ e o símbolo de entrada atual é 1, então ele pula deterministicamente para o estado S ₁ . Um DFA tem um estado inicial (denotado graficamente por uma seta vinda do nada) onde os cálculos começam e um conjunto de estados de aceitação (denotados graficamente por um círculo duplo) que ajudam a definir quando um cálculo é bem-sucedido.

Um DFA é definido como um conceito matemático abstrato, mas geralmente é implementado em hardware e software para resolver vários problemas específicos, como análise lexical e correspondência de padrões . Por exemplo, um DFA pode modelar um software que decide se a entrada do usuário online, como endereços de e-mail, é sintaticamente válida.

Os DFAs foram generalizados para autômatos finitos não determinísticos (NFA), que podem ter várias setas do mesmo rótulo a partir de um estado. Usando o método de construção PowerSet , cada NFA pode ser traduzido para um DFA que reconhece o mesmo idioma. DFAs, e NFAs também, reconhecem exatamente o conjunto de linguagens regulares .

Definição formal

Um autômato finito determinístico M é uma 5- tupla , ( Q , Σ, δ , q ₀ , F ) , consistindo em

• um conjunto finito de estados Q
• um conjunto finito de símbolos de entrada chamado alfabeto Σ
• uma função de transição δ  : Q × Σ → Q
• um estado inicial ou inicial ${\ displaystyle q_ {0} \ in Q}$
• um conjunto de estados de aceitação ${\ displaystyle F \ subseteq Q}$

Seja w = a ₁ a ₂ … a _n uma string sobre o alfabeto Σ . O autômato M aceita a string w se uma sequência de estados, r ₀ , r ₁ , ..., r _n , existe em Q com as seguintes condições:

1. r ₀ = q ₀
2. r _{i +1} = δ ( r _i , a _{i +1} ) , para i = 0,…, n - 1
3. ${\ displaystyle r_ {n} \ in F}$ .

Em palavras, a primeira condição diz que a máquina inicia no estado inicial q ₀ . A segunda condição diz que, dado cada caractere da string w , a máquina fará a transição de um estado para outro de acordo com a função de transição δ . A última condição diz que a máquina aceita w se a última entrada de w fizer com que a máquina pare em um dos estados de aceitação. Caso contrário, diz-se que o autômato rejeita a corda. O conjunto de strings que M aceita é a linguagem reconhecida por M e esta linguagem é denotada por L ( M ) .

Um autômato finito determinístico sem estados de aceitação e sem um estado inicial é conhecido como sistema de transição ou semiautomático .

Para uma introdução mais abrangente da definição formal, consulte a teoria dos autômatos .

Completo e incompleto

De acordo com a definição acima, autômatos finitos determinísticos são sempre completos : eles definem uma transição para cada estado e cada símbolo de entrada.

Embora esta seja a definição mais comum, alguns autores usam o termo autômato finito determinístico para uma noção ligeiramente diferente: um autômato que define no máximo uma transição para cada estado e cada símbolo de entrada; a função de transição pode ser parcial . Quando nenhuma transição é definida, tal autômato para.

Exemplo

O exemplo a seguir é de um DFA M , com um alfabeto binário, que requer que a entrada contenha um número par de 0s.

O diagrama de estado para M

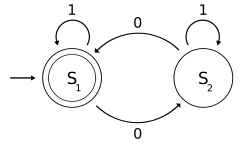
M = ( Q , Σ, δ , q ₀ , F ) onde

• Q = { S ₁ , S ₂ }
• Σ = {0, 1}
• q ₀ = S ₁
• F = { S ₁ } e
• δ é definido pela seguinte tabela de transição de estado :

	0	1
S 1	S 2	S 1
S 2	S 1	S 2

O estado S ₁ representa que houve um número par de 0s na entrada até agora, enquanto S ₂ significa um número ímpar. Um 1 na entrada não altera o estado do autômato. Quando a entrada terminar, o estado mostrará se a entrada continha um número par de 0s ou não. Se a entrada continha um número par de 0s, M terminará no estado S ₁ , um estado de aceitação, de modo que a string de entrada será aceita.

A linguagem reconhecida por M é a linguagem regular dada pela expressão regular (1*) (0 (1*) 0 (1*))* , onde * é a estrela de Kleene , por exemplo, 1* denota qualquer número (possivelmente zero) de unidades consecutivas.

Propriedades de fechamento

O autômato superior esquerdo reconhece a linguagem de todas as cadeias binárias contendo pelo menos uma ocorrência de "00". O autômato inferior direito reconhece todas as cadeias binárias com um número par de "1". O autômato inferior esquerdo é obtido como produto dos dois primeiros, ele reconhece a interseção das duas linguagens.

Se os DFAs reconhecerem os idiomas obtidos pela aplicação de uma operação nos idiomas reconhecíveis do DFA, os DFAs serão considerados encerrados na operação. Os DFAs são fechados nas seguintes operações.

Para cada operação, uma construção ótima em relação ao número de estados foi determinada na pesquisa de complexidade de estado . Uma vez que DFAs são equivalentes a autômatos finitos não determinísticos (NFA), esses fechamentos também podem ser provados usando propriedades de fechamento de NFA.

Como um monóide de transição

Uma execução de um determinado DFA pode ser vista como uma sequência de composições de uma formulação muito geral da função de transição consigo mesma. Aqui, construímos essa função.

Para um determinado símbolo de entrada , pode-se construir uma função de transição definindo para todos . (Esse truque é chamado de currying .) Dessa perspectiva, "atua" em um estado em Q para produzir outro estado. Pode-se então considerar o resultado de composição de função repetidamente aplicado às várias funções , e assim por diante. Dado um par de letras , pode-se definir uma nova função , onde denota a composição da função. ${\ displaystyle a \ in \ Sigma}$${\ displaystyle \ delta _ {a}: Q \ rightarrow Q}$${\ displaystyle \ delta _ {a} (q) = \ delta (q, a)}$${\ displaystyle q \ in Q}$${\ displaystyle \ delta _ {a}}$${\ displaystyle \ delta _ {a}}$${\ displaystyle \ delta _ {b}}$${\ displaystyle a, b \ in \ Sigma}$${\ displaystyle {\ widehat {\ delta}} _ {ab} = \ delta _ {a} \ circ \ delta _ {b}}$${\ displaystyle \ circ}$

Claramente, este processo pode ser continuado recursivamente, dando a seguinte definição recursiva de : ${\ displaystyle {\ widehat {\ delta}}: Q \ times \ Sigma ^ {\ star} \ rightarrow Q}$

${\ displaystyle {\ widehat {\ delta}} (q, \ epsilon) = q}$ , onde está a string vazia e ${\ displaystyle \ epsilon}$

${\ displaystyle {\ widehat {\ delta}} (q, wa) = \ delta _ {a} ({\ widehat {\ delta}} (q, w))}$ , onde e . ${\ displaystyle w \ in \ Sigma ^ {*}, a \ in \ Sigma}$${\ displaystyle q \ in Q}$

${\ displaystyle {\ widehat {\ delta}}}$ é definido para todas as palavras . Uma execução do DFA é uma sequência de composições de si mesma. ${\ displaystyle w \ in \ Sigma ^ {*}}$${\ displaystyle {\ widehat {\ delta}}}$

A composição de funções repetidas forma um monóide . Para as funções de transição, esse monóide é conhecido como monóide de transição ou, às vezes, semigrupo de transformação . A construção também pode ser revertida: dado a , pode-se reconstruir a e, portanto, as duas descrições são equivalentes. ${\ displaystyle {\ widehat {\ delta}}}$${\ displaystyle \ delta}$

Autômatos locais

Um autômato local é um DFA, não necessariamente completo, para o qual todas as arestas com o mesmo rótulo levam a um único vértice. Autômatos locais aceitam a classe de idiomas locais , aqueles para os quais a associação de uma palavra no idioma é determinada por uma "janela deslizante" de comprimento dois na palavra.

Um gráfico Myhill sobre um alfabeto A é um gráfico direcionado com conjunto de vértices A e subconjuntos de vértices rotulados como "início" e "término". A linguagem aceita por um grafo Myhill é o conjunto de caminhos direcionados de um vértice inicial ao vértice final: o grafo, portanto, atua como um autômato. A classe de idiomas aceitos pelos gráficos Myhill é a classe de idiomas locais.

Aleatória

Quando o estado inicial e os estados de aceitação são ignorados, um DFA de n estados e um alfabeto de tamanho k podem ser vistos como um dígrafo de n vértices em que todos os vértices têm k arcos externos rotulados 1, ..., k (a k- out dígrafo). Sabe-se que quando k ≥ 2 é um número inteiro fixo, com alta probabilidade, o maior componente fortemente conectado (SCC) em tal dígrafo k- out escolhido uniformemente ao acaso é de tamanho linear e pode ser alcançado por todos os vértices. Também foi provado que se k aumentar à medida que n aumenta, então todo o digrafo tem uma transição de fase para conectividade forte semelhante ao modelo Erdős-Rényi para conectividade.

Em um DFA aleatório, o número máximo de vértices alcançáveis ​​de um vértice é muito próximo ao número de vértices no maior SCC com alta probabilidade. Isso também é verdadeiro para o maior subdígrafo induzido de mínimo em grau um, que pode ser visto como uma versão direcionada de 1 -core .

Vantagens e desvantagens

Os DFAs são um dos modelos mais práticos de computação, uma vez que existe um algoritmo online trivial de tempo linear, espaço constante, para simular um DFA em um fluxo de entrada. Além disso, existem algoritmos eficientes para encontrar um DFA que reconheça:

• o complemento da linguagem reconhecida por um determinado DFA.
• a união / interseção das línguas reconhecidas por dois DFAs dados.

Como os DFAs podem ser reduzidos a uma forma canônica ( DFAs mínimos ), também existem algoritmos eficientes para determinar:

• se um DFA aceita quaisquer strings (problema de vazio)
• se um DFA aceita todas as strings (problema de universalidade)
• se dois DFAs reconhecem o mesmo idioma (problema de igualdade)
• se o idioma reconhecido por um DFA está incluído no idioma reconhecido por um segundo DFA (problema de inclusão)
• o DFA com um número mínimo de estados para um determinado idioma regular (problema de minimização)

Os DFAs são equivalentes em poder de computação aos autômatos finitos não determinísticos (NFAs). Isso ocorre porque, em primeiro lugar, qualquer DFA também é um NFA, então um NFA pode fazer o que um DFA pode fazer. Além disso, dado um NFA, usando a construção do conjunto de poderes, pode-se construir um DFA que reconheça a mesma linguagem do NFA, embora o DFA possa ter um número exponencialmente maior de estados do que o NFA. No entanto, embora os NFAs sejam computacionalmente equivalentes aos DFAs, os problemas mencionados acima não são necessariamente resolvidos de forma eficiente também para os NFAs. O problema de não universalidade para NFAs é PSPACE completo, uma vez que existem pequenos NFAs com a palavra de rejeição mais curta em tamanho exponencial. Um DFA é universal se e somente se todos os estados forem estados finais, mas isso não vale para NFAs. Os problemas de igualdade, inclusão e minimização também são PSPACE completos, uma vez que requerem a formação do complemento de um NFA que resulta em uma explosão exponencial de tamanho.

Por outro lado, os autômatos de estado finito têm um poder estritamente limitado nas linguagens que podem reconhecer; muitas linguagens simples, incluindo qualquer problema que requeira mais do que espaço constante para ser resolvido, não podem ser reconhecidas por um DFA. O exemplo clássico de uma linguagem descrita de forma simples que nenhum DFA pode reconhecer é a linguagem de colchetes ou Dyck , ou seja, a linguagem que consiste em colchetes emparelhados adequadamente, como a palavra "(() ())". Intuitivamente, nenhum DFA pode reconhecer a linguagem Dyck porque os DFAs não são capazes de contar: um autômato semelhante ao DFA precisa ter um estado para representar qualquer número possível de parênteses "abertos no momento", o que significa que precisaria de um número ilimitado de estados. Outro exemplo mais simples é a linguagem que consiste em cadeias de caracteres na forma a ⁿ b ⁿ para algum número finito mas arbitrário de a 's, seguido por um número igual de b ' s.

Identificação DFA de palavras rotuladas

Dado um conjunto de palavras positivas e um conjunto de palavras negativas, pode-se construir um DFA que aceita todas as palavras de e rejeita todas as palavras de : este problema é chamado de identificação DFA (síntese, aprendizagem). Embora algum DFA possa ser construído em tempo linear, o problema de identificar um DFA com o número mínimo de estados é NP-completo. O primeiro algoritmo para identificação DFA mínima foi proposto por Trakhtenbrot e Barzdin em e é chamado de algoritmo TB . No entanto, o algoritmo TB assume que todas as palavras de até um determinado comprimento estão contidas em qualquer um deles . ${\ displaystyle S ^ {+} \ subset \ Sigma ^ {*}}$${\ displaystyle S ^ {-} \ subset \ Sigma ^ {*}}$${\ displaystyle S ^ {+}}$${\ displaystyle S ^ {-}}$${\ displaystyle \ Sigma}$${\ displaystyle S ^ {+} \ cup S ^ {-}}$

Mais tarde, K. Lang propôs uma extensão da TB-algoritmo que não usa quaisquer suposições sobre e o Traxbar algoritmo. No entanto, o Traxbar não garante a minimalidade do DFA construído. Em seu trabalho, EM Gold também propôs um algoritmo heurístico para identificação mínima de DFA. O algoritmo de Gold assume isso e contém um conjunto de características da linguagem regular; caso contrário, o DFA construído será inconsistente com ou . Outros algoritmos de identificação DFA notáveis ​​incluem o algoritmo RPNI, o algoritmo de fusão de estados baseado em evidências Blue-Fringe, Windowed-EDSM. Outra direção de pesquisa é a aplicação de algoritmos evolutivos : o algoritmo evolucionário de rotulagem de estado inteligente permitiu resolver um problema de identificação DFA modificado no qual os dados de treinamento (conjuntos e ) são ruidosos no sentido de que algumas palavras são atribuídas a classes erradas. ${\ displaystyle S ^ {+}}$${\ displaystyle S ^ {-}}$${\ displaystyle S ^ {+}}$${\ displaystyle S ^ {-}}$${\ displaystyle S ^ {+}}$${\ displaystyle S ^ {-}}$${\ displaystyle S ^ {+}}$${\ displaystyle S ^ {-}}$

Ainda outro passo em frente é devido à aplicação de solucionadores SAT por Marjin J..H. Heule e S. Verwer: o problema mínimo de identificação de DFA é reduzido para decidir a satisfatibilidade de uma fórmula booleana. A ideia principal é construir um aceitador de árvore de prefixo aumentado (um trie contendo todas as palavras de entrada com rótulos correspondentes) com base nos conjuntos de entrada e reduzir o problema de encontrar um DFA com estados para colorir os vértices da árvore com estados de tal forma que quando vértices com uma cor são fundidos em um estado, o autômato gerado é determinístico e está em conformidade com e . Embora essa abordagem permita encontrar o DFA mínimo, ela sofre uma explosão exponencial do tempo de execução quando o tamanho dos dados de entrada aumenta. Portanto, o algoritmo inicial de Heule e Verwer foi posteriormente aprimorado com a realização de várias etapas do algoritmo EDSM antes da execução do solucionador SAT: o algoritmo DFASAT. Isso permite reduzir o espaço de busca do problema, mas leva à perda da garantia de minimalidade. Outra forma de reduzir o espaço de busca foi proposta por meio de novos predicados de quebra de simetria baseados no algoritmo de busca em amplitude : os estados do DFA procurados são limitados a serem numerados de acordo com o algoritmo BFS lançado a partir do estado inicial. Esta abordagem reduz o espaço de busca ao eliminar autômatos isomórficos. ${\ displaystyle C}$${\ displaystyle C}$${\ displaystyle S ^ {+}}$${\ displaystyle S ^ {-}}$${\ displaystyle C!}$

Veja também

Notas

Referências

• Hopcroft, John E .; Motwani, Rajeev ; Ullman, Jeffrey D. (2001). Introdução à Teoria dos Autômatos, Linguagens e Computação (2 ed.). Addison Wesley . ISBN   0-201-44124-1 . Página visitada em 19 de novembro de 2012 .
• Lawson, Mark V. (2004). Autômatos finitos . Chapman e Hall / CRC. ISBN   1-58488-255-7 . Zbl   1086.68074 .
• McCulloch, WS; Pitts, W. (1943). "Um cálculo lógico das idéias imanentes na atividade nervosa". Bulletin of Mathematical Biophysics . 5 (4): 115–133. doi : 10.1007 / BF02478259 . PMID   2185863 .
• Rabin, MO; Scott, D. (1959). "Autômatos finitos e seus problemas de decisão" . IBM J. Res. Dev . 3 (2): 114–125. doi : 10.1147 / rd.32.0114 .
• Sakarovitch, Jacques (2009). Elementos da teoria dos autômatos . Traduzido do francês por Reuben Thomas. Cambridge: Cambridge University Press . ISBN   978-0-521-84425-3 . Zbl   1188.68177 .
• Sipser, Michael (1997). Introdução à Teoria da Computação . Boston: PWS. ISBN   0-534-94728-X . . Seção 1.1: Finite Automata, pp. 31-47. Subseção "Decidable Problems Concerning Regular Languages" da seção 4.1: Decidable Languages, pp. 152-155.4.4 O DFA pode aceitar apenas linguagem regular