Correlação intraclasse - Intraclass correlation

Um gráfico de pontos mostrando um conjunto de dados com alta correlação intraclasse. Os valores do mesmo grupo tendem a ser semelhantes.

Um gráfico de pontos mostrando um conjunto de dados com baixa correlação intraclasse. Não há tendência de valores do mesmo grupo serem semelhantes.

Em estatística , a correlação intraclasse , ou coeficiente de correlação intraclasse ( ICC ), é uma estatística descritiva que pode ser usada quando medidas quantitativas são feitas em unidades organizadas em grupos. Ele descreve o quão fortemente as unidades no mesmo grupo se assemelham. Embora seja visto como um tipo de correlação , ao contrário da maioria das outras medidas de correlação, ele opera em dados estruturados como grupos, em vez de dados estruturados como observações emparelhadas.

A correlação intraclasse é comumente usada para quantificar o grau em que os indivíduos com um grau fixo de parentesco (por exemplo, irmãos completos) se assemelham em termos de uma característica quantitativa (ver herdabilidade ). Outra aplicação proeminente é a avaliação da consistência ou reprodutibilidade de medições quantitativas feitas por diferentes observadores medindo a mesma quantidade.

Definição ICC inicial: fórmula imparcial, mas complexa

Os primeiros trabalhos sobre correlações intraclasse focaram no caso de medidas pareadas, e a primeira estatística de correlação intraclasse (ICC) a ser proposta foram modificações da correlação interclasse (correlação de Pearson).

Considere-se um conjunto de dados consistindo de N emparelhado valores de dados ( x _{n , 1} , x _{n , 2} ), para n = 1, ..., N . A correlação intraclasse r originalmente proposta por Ronald Fisher é

{\ displaystyle r = {\ frac {1} {Ns ^ {2}}} \ sum _ {n = 1} ^ {N} (x_ {n, 1} - {\ bar {x}}) (x_ { n, 2} - {\ bar {x}}),}

Onde

{\ displaystyle {\ bar {x}} = {\ frac {1} {2N}} \ sum _ {n = 1} ^ {N} (x_ {n, 1} + x_ {n, 2}),}

{\ displaystyle s ^ {2} = {\ frac {1} {2N}} \ left \ {\ sum _ {n = 1} ^ {N} (x_ {n, 1} - {\ bar {x}} ) ^ {2} + \ sum _ {n = 1} ^ {N} (x_ {n, 2} - {\ bar {x}}) ^ {2} \ direita \}.}

Versões posteriores dessa estatística usaram os graus de liberdade 2 N −1 no denominador para calcular s ² e N −1 no denominador para calcular r , de modo que s ² torna-se não enviesado e r torna-se não enviesado se s for conhecido.

A principal diferença entre este ICC e a correlação interclasse (Pearson) é que os dados são combinados para estimar a média e a variância. A razão para isso é que, no cenário onde uma correlação intraclasse é desejada, os pares são considerados não ordenados. Por exemplo, se estamos estudando a semelhança de gêmeos, geralmente não há uma maneira significativa de ordenar os valores para os dois indivíduos dentro de um par de gêmeos. Como a correlação interclasse, a correlação intraclasse para dados emparelhados será confinada ao intervalo [-1, +1].

A correlação intraclasse também é definida para conjuntos de dados com grupos com mais de 2 valores. Para grupos que consistem em três valores, é definido como

{\ displaystyle r = {\ frac {1} {3Ns ^ {2}}} \ sum _ {n = 1} ^ {N} \ left \ {(x_ {n, 1} - {\ bar {x}} ) (x_ {n, 2} - {\ bar {x}}) + (x_ {n, 1} - {\ bar {x}}) (x_ {n, 3} - {\ bar {x}}) + (x_ {n, 2} - {\ bar {x}}) (x_ {n, 3} - {\ bar {x}}) \ direita \},}

Onde

{\ displaystyle {\ bar {x}} = {\ frac {1} {3N}} \ sum _ {n = 1} ^ {N} (x_ {n, 1} + x_ {n, 2} + x_ { n, 3}),}

{\ displaystyle s ^ {2} = {\ frac {1} {3N}} \ left \ {\ sum _ {n = 1} ^ {N} (x_ {n, 1} - {\ bar {x}} ) ^ {2} + \ sum _ {n = 1} ^ {N} (x_ {n, 2} - {\ bar {x}}) ^ {2} + \ sum _ {n = 1} ^ {N } (x_ {n, 3} - {\ bar {x}}) ^ {2} \ direita \}.}

À medida que o número de itens por grupo aumenta, também aumenta o número de termos de produtos cruzados nesta expressão. A seguinte forma equivalente é mais simples de calcular:

{\ displaystyle r = {\ frac {K} {K-1}} \ cdot {\ frac {N ^ {- 1} \ sum _ {n = 1} ^ {N} ({\ bar {x}} _ {n} - {\ bar {x}}) ^ {2}} {s ^ {2}}} - {\ frac {1} {K-1}},}

em que K é o número de valores de dados em cada grupo, e é a média da amostra do n ^th grupo. Essa forma geralmente é atribuída a Harris . O termo esquerdo não é negativo; consequentemente, a correlação intraclasse deve satisfazer ${\ displaystyle {\ bar {x}} _ {n}}$

{\ displaystyle r \ geq {\ frac {-1} {K-1}}.}

Para grande K , este ICC é quase igual a

{\ displaystyle {\ frac {N ^ {- 1} \ sum _ {n = 1} ^ {N} ({\ bar {x}} _ {n} - {\ bar {x}}) ^ {2} } {s ^ {2}}},}

que pode ser interpretado como a fração da variância total que é devida à variação entre os grupos. Ronald Fisher dedica um capítulo inteiro à correlação intraclasse em seu livro clássico Statistical Methods for Research Workers .

Para dados de uma população que é completamente ruído, a fórmula de Fisher produz valores de ICC que são distribuídos em cerca de 0, ou seja, às vezes sendo negativos. Isso ocorre porque Fisher projetou a fórmula para ser imparcial e, portanto, suas estimativas às vezes superestimam e às vezes subestimam. Para valores subjacentes pequenos ou zero na população, o ICC calculado a partir de uma amostra pode ser negativo.

Definições modernas de ICC: fórmula mais simples, mas tendência positiva

Começando com Ronald Fisher, a correlação intraclasse foi considerada no âmbito da análise de variância (ANOVA) e, mais recentemente, no âmbito dos modelos de efeitos aleatórios . Vários estimadores ICC foram propostos. A maioria dos estimadores pode ser definida em termos do modelo de efeitos aleatórios

{\ displaystyle Y_ {ij} = \ mu + \ alpha _ {j} + \ varepsilon _ {ij},}

onde Y _ij é a i ^ésima observação no j ^ésimo grupo, μ é uma média geral não observada , α _j é um efeito aleatório não observado compartilhado por todos os valores no grupo j , e ε _ij é um termo de ruído não observado. Para que o modelo seja identificado, assume-se que α _j e ε _ij têm valor esperado zero e não estão correlacionados entre si. Além disso, assume-se que o α _j está distribuído de forma idêntica, e o ε _ij é assumido como sendo distribuído de forma idêntica. A variância de α _j é denotada por σ²
_αe a variância de ε _ij é denotada por σ²
_ε.

O ICC da população nesta estrutura é:

{\ displaystyle {\ frac {\ sigma _ {\ alpha} ^ {2}} {\ sigma _ {\ alpha} ^ {2} + \ sigma _ {\ varepsilon} ^ {2}}}.}

Com esta estrutura, o ICC é a correlação de duas observações do mesmo grupo.

[Prova]

Para um modelo de efeitos aleatórios unilateral:

${\ displaystyle Y_ {ij} = \ mu + \ alpha _ {i} + \ epsilon _ {ij}}$

${\ displaystyle \ alpha _ {i} \ sim N (0, \ sigma _ {\ alpha} ^ {2})}$ , , S e s independente e s são independentes s. ${\ displaystyle \ epsilon _ {ij} \ sim N (0, \ sigma ^ {2})}$ ${\ displaystyle \ alpha _ {i}}$ ${\ displaystyle \ epsilon _ {ij}}$ ${\ displaystyle \ alpha _ {i}}$ ${\ displaystyle \ epsilon _ {ij}}$

A variância de qualquer observação é: A covariância de duas observações do mesmo grupo i (para ) é: ${\ displaystyle Var (Y_ {ij}) = \ sigma ^ {2} + \ sigma _ {\ alpha} ^ {2}}$ ${\ displaystyle j \ neq k}$

${\ displaystyle {\ begin {align} {\ text {Cov}} (Y_ {ij}, Y_ {ik}) & = {\ text {Cov}} (\ mu + \ alpha _ {i} + \ epsilon _ {ij}, \ mu + \ alpha _ {i} + \ epsilon _ {ik}) \\ & = {\ text {Cov}} (\ alpha _ {i} + \ epsilon _ {ij}, \ alpha _ {i} + \ epsilon _ {ik}) = {\ text {Cov}} (\ alpha _ {i}, \ alpha _ {i}) + 2 {\ text {Cov}} (\ alpha _ {i} , \ epsilon _ {ik}) + {\ text {Cov}} (\ epsilon _ {ij}, \ epsilon _ {ik}) \\ & = {\ text {Cov}} (\ alpha _ {i}, \ alpha _ {i}) = {\ text {Var}} (\ alpha _ {i}) \\ & = \ sigma _ {\ alpha} ^ {2}. \\\ fim {alinhado}}}$

Nisto, usamos propriedades da covariância .

Juntos, obtemos: ${\ displaystyle {\ text {Cor}} (Y_ {ij}, Y_ {ik}) = {\ frac {{\ text {Cov}} (Y_ {ij}, Y_ {ik})} {\ sqrt {Var (Y_ {ij}) Var (Y_ {ik})}}} = {\ frac {\ sigma _ {\ alpha} ^ {2}} {\ sigma ^ {2} + \ sigma _ {\ alpha} ^ { 2}}}}$

Uma vantagem dessa estrutura ANOVA é que grupos diferentes podem ter números diferentes de valores de dados, o que é difícil de manipular usando as estatísticas ICC anteriores. Este ICC é sempre não negativo, permitindo que seja interpretado como a proporção da variância total que está "entre grupos". Este ICC pode ser generalizado para permitir efeitos de covariável, caso em que o ICC é interpretado como capturando a similaridade dentro da classe dos valores de dados ajustados por covariável.

Esta expressão nunca pode ser negativa (ao contrário da fórmula original de Fisher) e, portanto, em amostras de uma população que tem um ICC de 0, os ICCs nas amostras serão maiores do que o ICC da população.

Várias estatísticas ICC diferentes foram propostas, nem todas estimando o mesmo parâmetro populacional. Tem havido um debate considerável sobre quais estatísticas ICC são apropriadas para um determinado uso, uma vez que podem produzir resultados marcadamente diferentes para os mesmos dados.

Relação com o coeficiente de correlação de Pearson

Em termos de sua forma algébrica, o ICC original de Fisher é o ICC que mais se assemelha ao coeficiente de correlação de Pearson . Uma diferença importante entre as duas estatísticas é que no ICC, os dados são centralizados e escalonados usando uma média e desvio padrão agrupados, enquanto na correlação de Pearson, cada variável é centralizada e escalonada por sua própria média e desvio padrão. Esta escala combinada para o ICC faz sentido porque todas as medições são da mesma quantidade (embora em unidades em grupos diferentes). Por exemplo, em um conjunto de dados emparelhados onde cada "par" é uma única medida feita para cada uma das duas unidades (por exemplo, pesando cada gêmeo em um par de gêmeos idênticos) em vez de duas medidas diferentes para uma única unidade (por exemplo, medir a altura e peso para cada indivíduo), o ICC é uma medida de associação mais natural do que a correlação de Pearson.

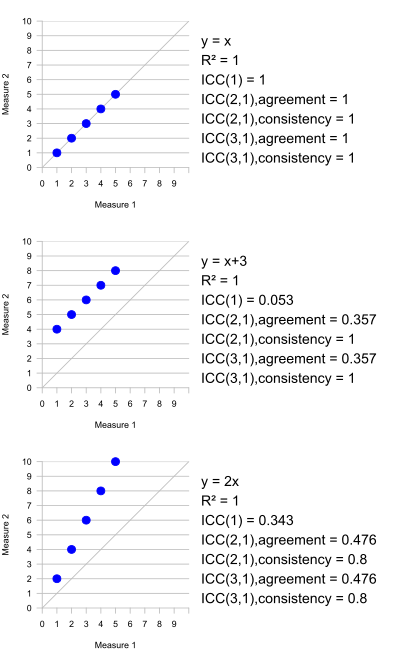
Uma propriedade importante da correlação de Pearson é que ela é invariante à aplicação de transformações lineares separadas às duas variáveis que estão sendo comparadas. Assim, se estivermos correlacionando X e Y , onde, digamos, Y = 2 X + 1, a correlação de Pearson entre X e Y é 1 - uma correlação perfeita. Esta propriedade não faz sentido para o ICC, uma vez que não há base para decidir qual transformação é aplicada a cada valor em um grupo. No entanto, se todos os dados em todos os grupos estão sujeitos à mesma transformação linear, o ICC não muda.

Uso na avaliação de conformidade entre observadores

O ICC é usado para avaliar a consistência, ou conformidade, das medições feitas por vários observadores medindo a mesma quantidade. Por exemplo, se vários médicos forem solicitados a pontuar os resultados de uma tomografia computadorizada para detectar sinais de progressão do câncer, podemos perguntar se as pontuações são consistentes entre si. Se a verdade for conhecida (por exemplo, se as tomografias computadorizadas foram em pacientes que subseqüentemente foram submetidos à cirurgia exploratória), então o foco geralmente seria em quão bem as pontuações dos médicos corresponderam à verdade. Se a verdade não for conhecida, podemos apenas considerar a semelhança entre as pontuações. Um aspecto importante deste problema é que não há tanto inter-observador ea variabilidade intra-observador. A variabilidade interobservador refere-se a diferenças sistemáticas entre os observadores - por exemplo, um médico pode pontuar consistentemente os pacientes em um nível de risco mais alto do que outros médicos. A variabilidade intra-observador refere-se a desvios da pontuação de um observador específico em um paciente específico que não fazem parte de uma diferença sistemática.

O ICC é construído para ser aplicado a medições intercambiáveis - isto é, dados agrupados nos quais não há uma maneira significativa de ordenar as medições dentro de um grupo. Ao avaliar a conformidade entre os observadores, se os mesmos observadores classificam cada elemento que está sendo estudado, então é provável que existam diferenças sistemáticas entre os observadores, o que entra em conflito com a noção de permutabilidade. Se o ICC for usado em uma situação onde existem diferenças sistemáticas, o resultado é uma medida composta de variabilidade intra-observador e inter-observador. Uma situação em que a permutabilidade pode ser razoavelmente presumida como válida seria quando uma amostra a ser pontuada, digamos uma amostra de sangue, é dividida em múltiplas alíquotas e as alíquotas são medidas separadamente no mesmo instrumento. Neste caso, a permutabilidade seria mantida enquanto nenhum efeito devido à sequência de execução das amostras estivesse presente.

Uma vez que o coeficiente de correlação intraclasse fornece uma composição da variabilidade intra-observador e interobservador, seus resultados às vezes são considerados difíceis de interpretar quando os observadores não são trocáveis. Medidas alternativas como a estatística kappa de Cohen , o Fleiss kappa e o coeficiente de correlação de concordância foram propostas como medidas de concordância mais adequadas entre observadores não trocáveis.

Cálculo em pacotes de software

Diferentes definições de coeficientes de correlação intraclasse aplicadas a três cenários de concordância interobservador.

ICC é suportado no pacote de software de código aberto R (usando a função "icc" com os pacotes psy ou irr , ou através da função "ICC" no pacote psych .) O pacote rptR fornece métodos para a estimativa de ICC e repetibilidade para Dados distribuídos gaussianos, binomiais e de Poisson em uma estrutura de modelos mistos. Notavelmente, o pacote permite estimar o ICC ajustado (isto é, controlar outras variáveis) e computar intervalos de confiança com base em bootstrapping paramétrico e significâncias com base na permutação de resíduos. O software comercial também suporta ICC, por exemplo Stata ou SPSS

Diferentes tipos de ICC [3] Arquivado em 03/03/2009 na Máquina Wayback
Convenção Shrout e Fleiss	Convenção McGraw e Wong	Nome em SPSS e Stata
ICC (1,1)	Aleatório unilateral, pontuação única ICC (1)	Medidas aleatórias unilaterais
ICC (2,1)	Aleatório bidirecional, pontuação única ICC (A, 1)	Aleatório bidirecional, medidas únicas, concordância absoluta
ICC (3,1)	Duas vias misto, pontuação única ICC (C, 1)	Misto bidirecional, medidas simples, consistência
Indefinido	Aleatório bidirecional, pontuação única ICC (C, 1)	Aleatório bidirecional, medidas únicas, consistência
Indefinido	Duas vias misto, pontuação única ICC (A, 1)	Duas vias mistas, medidas simples, concordância absoluta
ICC (1, k)	Aleatório unilateral, pontuação média ICC (k)	Medidas médias aleatórias unilaterais
ICC (2, k)	Aleatório bidirecional, pontuação média ICC (A, k)	Aleatório bidirecional, medidas médias, concordância absoluta
ICC (3, k)	Duas vias misto, pontuação média ICC (C, k)	Duas vias mistas, medidas médias, consistência
Indefinido	Aleatório bidirecional, pontuação média ICC (C, k)	Aleatório bidirecional, medidas médias, consistência
Indefinido	Duas vias misto, pontuação média ICC (A, k)	Duas vias mistas, medidas médias, concordância absoluta

Os três modelos são:

Efeitos aleatórios unilaterais: cada sujeito é medido por um conjunto diferente de k avaliadores selecionados aleatoriamente;
Aleatório bidirecional: k avaliadores são selecionados aleatoriamente, então, cada sujeito é medido pelo mesmo conjunto de k avaliadores;
Duas vias mistas: k avaliadores fixos são definidos. Cada sujeito é medido pelos k avaliadores.

Número de medições:

Medidas únicas: mesmo que mais de uma medida seja tomada no experimento, a confiabilidade é aplicada a um contexto onde uma única medida de um único avaliador será realizada;
Medidas médias: a confiabilidade é aplicada a um contexto onde as medidas de k avaliadores serão calculadas para cada sujeito.

Consistência ou concordância absoluta:

Concordância absoluta: a concordância entre dois avaliadores é de interesse, incluindo erros sistemáticos de ambos os avaliadores e erros residuais aleatórios;
Consistência: no contexto de medições repetidas pelo mesmo avaliador, os erros sistemáticos do avaliador são cancelados e apenas o erro residual aleatório é mantido.

O ICC de consistência não pode ser estimado no modelo de efeitos aleatórios unilateral, pois não há como separar as variâncias interexaminadores e residuais.

Uma visão geral e reanálise dos três modelos para as medidas individuais ICC, com uma receita alternativa para seu uso, também foi apresentada por Liljequist et al (2019).

Interpretação

Cicchetti (1994) fornece as seguintes diretrizes frequentemente citadas para a interpretação de medidas de acordo kappa ou ICC entre avaliadores:

Menos de 0,40 - ruim.
Entre 0,40 e 0,59 - razoável.
Entre 0,60 e 0,74 - bom.
Entre 0,75 e 1,00 - excelente.

Uma orientação diferente é dada por Koo e Li (2016):

abaixo de 0,50: pobre
entre 0,50 e 0,75: moderado
entre 0,75 e 0,90: bom
acima de 0,90: excelente

Veja também

Referências

links externos

AgreeStat 360: análise de confiabilidade entre avaliadores baseada em nuvem, kappa de Cohen, AC1 / AC2 de Gwet, alfa de Krippendorff, Brennan-Prediger, kappa generalizado de Fleiss, coeficientes de correlação intraclasse
Uma ferramenta online útil que permite o cálculo dos diferentes tipos de ICC
Exemplo de estudo de Viecelli et al., Onde o ICC foi usado para determinar a confiabilidade entre avaliadores usando o coeficiente de correlação intraclasse (ICC 2.1).

^ Viecelli C, Graf D, Aguayo D, Hafen E, Füchslin RM (2020-07-15). "Usando dados de acelerômetro de smartphone para obter descritores científicos mecânico-biológicos de treinamento de exercícios de resistência" . PLOS ONE . 15 (7): e0235156. Bibcode : 2020PLoSO..1535156V . doi : 10.1371 / journal.pone.0235156 . PMC 7363108 . PMID 32667945 .

[21] Viecelli C, Graf D, Aguayo D, Hafen E, Füchslin RM (2020-07-15). "Usando dados de acelerômetro de smartphone para obter descritores científicos mecânico-biológicos de treinamento de exercícios de resistência" . PLOS ONE . 15 (7): e0235156. Bibcode : 2020PLoSO..1535156V . doi : 10.1371 / journal.pone.0235156 . PMC 7363108 . PMID 32667945 .

Languages

In other projects