Equação de Scherrer - Scherrer equation

A equação de Scherrer , em difração de raios-X e cristalografia , é uma fórmula que relaciona o tamanho dos cristalitos submicrométricos em um sólido ao alargamento de um pico em um padrão de difração. É frequentemente referido, incorretamente, como uma fórmula para medição ou análise do tamanho de partícula. Tem o nome de Paul Scherrer . É utilizado na determinação do tamanho de cristais na forma de pó.

A equação de Scherrer pode ser escrita como:

${\ displaystyle \ tau = {\ frac {K \ lambda} {\ beta \ cos \ theta}}}$

Onde:

• ${\ displaystyle \ tau}$ é o tamanho médio dos domínios ordenados (cristalinos), que pode ser menor ou igual ao tamanho do grão, que pode ser menor ou igual ao tamanho da partícula;
• ${\ displaystyle K}$ é um fator de forma adimensional , com um valor próximo da unidade. O fator de forma tem um valor típico de cerca de 0,9, mas varia com a forma real do cristalito;
• ${\ displaystyle \ lambda}$ é o comprimento de onda do raio X ;
• ${\ displaystyle \ beta}$ é o alargamento da linha na metade da intensidade máxima ( FWHM ), após subtrair o alargamento da linha instrumental, em radianos . Essa quantidade também é às vezes indicada como ; ${\ displaystyle \ Delta \ left (2 \ theta \ right)}$
• ${\ displaystyle \ theta}$ é o ângulo de Bragg .

Aplicabilidade

A equação de Scherrer está limitado a nano cristalitos -scale, ou mais-estritamente, o tamanho do domínio coerentemente dispersão, que pode ser menor do que o tamanho de cristalito (devido a factores mencionados abaixo). Não é aplicável a grãos maiores do que cerca de 0,1 a 0,2 μm, o que exclui aqueles observados na maioria das microestruturas metalográficas e ceramográficas .

É importante perceber que a fórmula de Scherrer fornece um limite inferior no tamanho do domínio de espalhamento coerente, referido aqui como o tamanho do cristalito para legibilidade. A razão para isso é que uma variedade de fatores podem contribuir para a largura de um pico de difração, além dos efeitos instrumentais e do tamanho do cristalito; as mais importantes são geralmente deformações não homogêneas e imperfeições de rede cristalina. As seguintes fontes de alargamento de pico são deslocamentos, falhas de empilhamento, geminação, microestrutura, limites de grão, sublimites, deformação de coerência, heterogeneidades químicas e pequenez de cristalito. Estas e outras imperfeições também podem resultar em deslocamento de pico, assimetria de pico, alargamento de pico anisotrópico ou outros efeitos de formato de pico.

Se todas essas outras contribuições para a largura do pico, incluindo o alargamento instrumental, fossem zero, então a largura do pico seria determinada apenas pelo tamanho do cristalito e a fórmula de Scherrer se aplicaria. Se as outras contribuições para a largura forem diferentes de zero, então o tamanho do cristalito pode ser maior do que o previsto pela fórmula de Scherrer, com a largura do pico "extra" vindo de outros fatores. O conceito de cristalinidade pode ser usado para descrever coletivamente o efeito do tamanho do cristal e das imperfeições no alargamento do pico.

Embora "tamanho de partícula" seja freqüentemente usado em referência ao tamanho de cristalito, este termo não deve ser usado em associação com o método de Scherrer porque as partículas são frequentemente aglomerações de muitos cristalitos e o XRD não fornece informações sobre o tamanho da partícula. Outras técnicas, como peneiramento , análise de imagem ou dispersão de luz visível medem diretamente o tamanho das partículas. O tamanho do cristalito pode ser considerado um limite inferior do tamanho da partícula.

Derivação para uma pilha simples de aviões

Para ver de onde vem a equação de Scherrer, é útil considerar o exemplo mais simples possível: um conjunto de N planos separados pela distância, a . A derivação para este caso simples e efetivamente unidimensional é direta. Primeiro, o fator de estrutura para este caso é derivado e, em seguida, uma expressão para as larguras de pico é determinada.

Fator de estrutura para um conjunto de N planos igualmente espaçados

Este sistema, efetivamente um cristal perfeito unidimensional, tem um fator de estrutura ou função de espalhamento S (q):

${\ displaystyle S (q) = {\ frac {1} {N}} \ sum _ {j, k = 1} ^ {N} \ mathrm {e} ^ {- iq (x_ {j} -x_ {k })}}$

onde para N planos : ${\ displaystyle x_ {j} = aj}$

${\ displaystyle S (q) = {\ frac {1} {N}} \ sum _ {k = 1} ^ {N} \ mathrm {e} ^ {- iqak} \ times \ sum _ {j = 1} ^ {N} \ mathrm {e} ^ {iqaj}}$

Fator de estrutura S (qa) para N = 31 planos. São mostrados o primeiro e o segundo picos de Bragg. É importante notar que, para uma rede perfeita, mas finita, todos os picos são idênticos. Em particular, todos os picos têm a mesma largura. Além disso, a parte central (entre os zeros entre parênteses) de cada pico está perto de uma função gaussiana , mas o envelope das pequenas oscilações em cada lado desse pico é uma função Lorentziana .

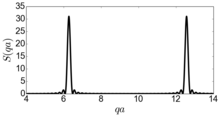
cada soma é uma série geométrica simples, definindo , e a outra série de forma análoga dá: ${\ displaystyle y = \ exp (iqa)}$${\ textstyle \ sum _ {j = 1} ^ {N} y ^ {j} = (yy ^ {N + 1}) / (1-y)}$

${\ displaystyle S (q) = {\ frac {1} {N}} {\ frac {\ left [{\ rm {e}} ^ {- iqa} - {\ rm {e}} ^ {- iqa ( N + 1)} \ right]} {\ left [1-e ^ {- iqa} \ right]}} \ times {\ frac {\ left [{\ rm {e}} ^ {iqa} - {\ rm {e}} ^ {iqa (N + 1)} \ direita]} {\ esquerda [1-e ^ {iqa} \ direita]}}}$

${\ displaystyle S (q) = {\ frac {1} {N}} {\ frac {2 - {\ rm {e}} ^ {iqaN} - {\ rm {e}} ^ {- iqaN}} { 2 - {\ rm {e}} ^ {iqa} - {\ rm {e}} ^ {- iqa}}}}$

que é ainda mais simplificado pela conversão para funções trigonométricas:

${\ displaystyle S (q) = {\ frac {1} {N}} {\ frac {1- \ cos [Nqa]} {1- \ cos [qa]}}}$

e finalmente:

${\ displaystyle S (q) = {\ frac {1} {N}} {\ frac {\ sin ^ {2} [Nqa / 2]} {\ sin ^ {2} [qa / 2]}}}$

o que dá um conjunto de picos em , todos com alturas . ${\ textstyle q_ {P} = 0,2 \ pi / a, 4 \ pi / a, \ ldots}$${\ displaystyle S (q_ {P}) = N}$

Determinação do perfil perto do pico e, portanto, a largura do pico

A partir da definição de FWHM, para um pico a e com um FWHM de , , como a altura do pico é N . Se pegarmos o sinal de mais (o pico é simétrico, então qualquer um dos sinais serve) ${\ textstyle q_ {P}}$${\ textstyle \ Delta q}$${\ displaystyle S (q_ {P} \ pm \ Delta q / 2) = S (q_ {P}) / 2 = N / 2}$

${\ displaystyle S (q_ {P} + \ Delta q / 2) = {\ frac {1} {N}} {\ frac {\ sin ^ {2} [Na (q_ {P} + \ Delta q / 2 ) / 2]} {\ sin ^ {2} [a (q_ {P} + \ Delta q / 2) / 2]}} = {\ frac {1} {N}} \ left [{\ frac {\ sin [Na (q_ {P} + \ Delta q / 2) / 2]} {\ sin [a (q_ {P} + \ Delta q / 2) / 2]}} \ right] ^ {2} = N / 2}$

e

${\ displaystyle {\ frac {\ sin [Na (q_ {P} + \ Delta q / 2) / 2]} {\ sin [a (q_ {P} + \ Delta q / 2) / 2]}} = {\ frac {\ sin [Na \ Delta q / 4]} {\ sin [a \ Delta q / 4]}} = {\ frac {N} {2 ^ {1/2}}}}$

se N não for muito pequeno. Se for pequeno, então , e podemos escrever a equação como uma única equação não linear , para . A solução para esta equação é . Portanto, o tamanho do conjunto de planos está relacionado ao FWHM em q por ${\ displaystyle \ Delta q}$${\ displaystyle \ sin [\ Delta qa / 4] \ simeq \ Delta qa / 4}$${\ displaystyle \ sin (x) - (x / 2 ^ {1/2}) = 0}$${\ displaystyle x = Na \ Delta q / 4}$${\ displaystyle x = 1,39}$

${\ displaystyle \ tau = Na = {\ frac {5.56} {\ Delta q}}}$

Para converter para uma expressão para o tamanho do cristal em termos da largura do pico no ângulo de espalhamento usado na difração de pó de raios- X , notamos que o vetor de espalhamento , onde o aqui é o ângulo entre o vetor de onda incidente e o vetor de onda espalhado, que é diferente do na digitalização. Então, a largura do pico na variável é aproximadamente , e assim ${\ displaystyle 2 \ theta}$${\ displaystyle q = (4 \ pi / \ lambda) \ sin (\ theta / 2)}$${\ displaystyle \ theta}$${\ displaystyle \ theta}$${\ displaystyle 2 \ theta}$${\ displaystyle 2 \ theta}$${\ displaystyle \ beta \ simeq 2 \ Delta q / [{\ rm {d}} q / {\ rm {d}} \ theta] = 2 \ Delta q / [(4 \ pi / \ lambda) \ cos ( \ theta)]}$

${\ displaystyle \ tau = Na = {\ frac {5,56 \ lambda} {2 \ pi \ beta \ cos (\ theta)}} = {\ frac {0,88 \ lambda} {\ beta \ cos (\ theta)}} }$

que é a equação de Scherrer com K = 0,88.

Isso se aplica apenas a um conjunto de aviões 1D perfeito. No caso 3D experimentalmente relevante, a forma e, portanto, os picos, depende do tipo de rede cristalina e do tamanho e forma do nanocristalito. A matemática subjacente torna-se mais envolvida do que neste exemplo ilustrativo simples. No entanto, para redes e formas simples, as expressões foram obtidas para o FWHM, por exemplo, por Patterson . Assim como em 1D, o FWHM varia como o inverso do tamanho característico. Por exemplo, para um cristalito esférico com uma rede cúbica, o fator de 5,56 simplesmente torna-se 6,96, quando o tamanho é o diâmetro D, ou seja, o diâmetro de um nanocristal esférico está relacionado ao pico FWHM por ${\ displaystyle S (q)}$

${\ displaystyle D = {\ frac {6.96} {\ Delta q}}}$ ou em : ${\ displaystyle \ theta}$${\ displaystyle D = {\ frac {1.11 \ lambda} {\ beta \ cos (\ theta)}}}$

Alargamento do pico devido à desordem do segundo tipo

O tamanho finito de um cristal não é a única razão possível para picos alargados na difração de raios-X . Flutuações de átomos sobre as posições ideais da rede que preservam a ordem de longo alcance da rede apenas dão origem ao fator de Debye-Waller , que reduz as alturas dos picos, mas não as amplia. No entanto, as flutuações que fazem com que as correlações entre os átomos próximos diminuam à medida que sua separação aumenta, ampliam os picos. Isso pode ser estudado e quantificado usando a mesma pilha unidimensional simples de planos acima. A derivação segue aquela no capítulo 9 do livro de Guinier . Este modelo foi desenvolvido e aplicado a diversos materiais por Hosemann e colaboradores ao longo de vários anos. Eles chamaram esse distúrbio de segundo tipo e se referiram a essa ordem cristalina imperfeita como ordem paracristalina . A desordem do primeiro tipo é a fonte do fator Debye-Waller .

Para derivar o modelo, começamos com a definição do fator de estrutura

${\ displaystyle S (q) = {\ frac {1} {N}} \ sum _ {j, k = 1} ^ {N} \ mathrm {e} ^ {- iq (x_ {j} -x_ {k })}}$

mas agora queremos considerar, para simplificar, um cristal infinito, isto é,, e queremos considerar pares de sítios de rede. Para grande , para cada um desses planos, existem dois planos vizinhos de distância, então a soma dupla acima se torna uma única soma sobre pares de vizinhos de cada lado de um átomo, em posições e espaçamentos de rede, vezes . Então ${\ displaystyle N \ to \ infty}$${\ displaystyle N}$${\ displaystyle N}$${\ displaystyle m}$${\ displaystyle -m}$${\ displaystyle m}$${\ displaystyle N}$

${\ displaystyle S (q) = 1 + {\ frac {2} {N}} \ sum _ {m = 1} ^ {N} \ int _ {- \ infty} ^ {\ infty} {\ rm {d }} (\ Delta x) p_ {m} (\ Delta x) \ cos \ left (mq \ Delta x \ right)}$

onde é a função de densidade de probabilidade para a separação de um par de planos, espaçamentos de rede separados. Para a separação de planos vizinhos, assumimos, por simplicidade, que as flutuações em torno do espaçamento médio vizinho de a são gaussianas, ou seja, que ${\ displaystyle p_ {m} (\ Delta x)}$${\ displaystyle \ Delta x}$${\ displaystyle m}$

${\ displaystyle p_ {1} (\ Delta x) = {\ frac {1} {\ left (2 \ pi \ sigma _ {2} ^ {2} \ right) ^ {1/2}}} \ exp \ esquerda [- \ esquerda (\ Delta xa \ direita) ^ {2} / (2 \ sigma _ {2} ^ {2}) \ direita]}$

e também assumimos que as flutuações entre um plano e seu vizinho, e entre este vizinho e o próximo plano, são independentes. Então é apenas a convolução de dois s, etc. Como a convolução de duas gaussianas é apenas outra gaussiana, temos que ${\ displaystyle p_ {2} (\ Delta x)}$${\ displaystyle p_ {1} (\ Delta x)}$

${\ displaystyle p_ {m} (\ Delta x) = {\ frac {1} {\ left (2 \ pi m \ sigma _ {2} ^ {2} \ right) ^ {1/2}}} \ exp \ left [- \ left (\ Delta x-ma \ right) ^ {2} / (2m \ sigma _ {2} ^ {2}) \ right]}$

A soma em é então apenas uma soma das Transformadas de Fourier de Gaussianas, e assim ${\ displaystyle S (q)}$

${\ displaystyle S (q) = 1 + 2 \ sum _ {m = 1} ^ {\ infty} r ^ {m} \ cos \ left (mqa \ right)}$

para . A soma é apenas a parte real da soma e, portanto, o fator de estrutura do cristal infinito mas desordenado é ${\ displaystyle r = \ exp [-q ^ {2} \ sigma _ {2} ^ {2} / 2]}$${\ displaystyle \ sum _ {m = 1} ^ {\ infty} [r \ exp (iqa)] ^ {m}}$

${\ displaystyle S (q) = {\ frac {1-r ^ {2}} {1 + r ^ {2} -2r \ cos (qa)}}}$

Isso tem picos no máximo , onde . Esses picos têm alturas ${\ displaystyle q_ {p} = 2n \ pi / a}$${\ displaystyle \ cos (q_ {P} a) = 1}$

${\ displaystyle S (q_ {P}) = {\ frac {1 + r} {1-r}} \ approx {\ frac {4} {q_ {P} ^ {2} \ sigma _ {2} ^ { 2}}} = {\ frac {a ^ {2}} {n ^ {2} \ pi ^ {2} \ sigma _ {2} ^ {2}}}}$

isto é, a altura dos picos sucessivos diminui conforme a ordem do pico (e assim ) ao quadrado. Ao contrário dos efeitos de tamanho finito que ampliam os picos, mas não diminuem sua altura, a desordem diminui as alturas dos picos. Observe que aqui estamos assumindo que o distúrbio é relativamente fraco, de modo que ainda temos picos relativamente bem definidos. Este é o limite , onde . Neste limite, perto de um pico podemos aproximar , com e obter ${\ displaystyle q}$${\ displaystyle q \ sigma _ {2} \ ll 1}$${\ displaystyle r \ simeq 1-q ^ {2} \ sigma _ {2} ^ {2} / 2}$${\ displaystyle \ cos (qa) \ simeq 1 - (\ Delta q) ^ {2} a ^ {2} / 2}$${\ displaystyle \ Delta q = q-q_ {P}}$

${\ displaystyle S (q) \ approx {\ frac {S (q_ {P})} {1 + {\ frac {r} {(1-r) ^ {2}}} \ Delta q ^ {2} a ^ {2}}} \ approx {\ frac {S (q_ {P})} {1 + {\ frac {\ Delta q ^ {2}} {[q_ {P} ^ {2} \ sigma _ {2 } ^ {2} / 2a] ^ {2}}}}}}$

que é uma função Lorentziana ou Cauchy , de FWHM , ou seja, o FWHM aumenta como o quadrado da ordem do pico, e assim como o quadrado do vetor de onda no pico. Finalmente, o produto da altura do pico e o FWHM é constante e igual , no limite. Para os primeiros picos em que não é grande, esse é apenas o limite. ${\ displaystyle q_ {P} ^ {2} \ sigma _ {2} ^ {2} / a = 4 \ pi ^ {2} n ^ {2} (\ sigma _ {2} / a) ^ {2} /uma}$${\ displaystyle q}$${\ displaystyle 4 / a}$${\ displaystyle q \ sigma _ {2} \ ll 1}$${\ displaystyle n}$${\ displaystyle \ sigma _ {2} / a \ ll 1}$

Portanto, o tamanho finito e esse tipo de distúrbio causam o alargamento do pico, mas há diferenças qualitativas. Os efeitos de tamanho finito ampliam todos os picos igualmente e não afetam as alturas dos picos, enquanto esse tipo de distúrbio reduz as alturas dos picos e amplia os picos em uma quantidade que aumenta conforme . Isso, em princípio, permite distinguir os dois efeitos. Além disso, significa que a equação de Scherrer é mais bem aplicada ao primeiro pico, pois a desordem desse tipo afeta menos o primeiro pico. ${\ displaystyle n ^ {2}}$

Comprimento de coerência

Dentro deste modelo, o grau de correlação entre um par de planos diminui à medida que a distância entre esses planos aumenta, ou seja, um par de planos com 10 planos de distância tem posições que são mais fracamente correlacionadas do que um par de planos que são vizinhos mais próximos. A correlação é dada por , para um par de planos separados por m planos. Para m suficientemente grande, o par de planos é essencialmente não correlacionado, no sentido de que a incerteza em suas posições relativas é tão grande que é comparável ao espaçamento da rede, a . Isso define um comprimento de correlação,, definido como a separação quando a largura de , que é igual a a . Isto dá ${\ displaystyle p_ {m}}$${\ displaystyle \ lambda}$${\ displaystyle p_ {m}}$${\ displaystyle m ^ {1/2} \ sigma _ {2}}$

${\ displaystyle \ lambda = {\ frac {a ^ {3}} {\ sigma _ {2} ^ {2}}}}$

que é com efeito uma estimativa de ordem de magnitude para o tamanho dos domínios de redes cristalinas coerentes. Observe que o FWHM das escalas do primeiro pico , portanto, o comprimento de coerência é de aproximadamente 1 / FWHM para o primeiro pico. ${\ displaystyle \ sigma _ {2} ^ {2} / a ^ {3}}$

Leitura adicional

• BD Cullity & SR Stock, Elements of X-Ray Diffraction , 3rd Ed., Prentice-Hall Inc., 2001, p 96-102, ISBN   0-201-61091-4 .
• R. Jenkins & RL Snyder, Introduction to X-ray Powder Diffractometry , John Wiley & Sons Inc., 1996, p 89-91, ISBN   0-471-51339-3 .
• HP Klug & LE Alexander, X-Ray Diffraction Procedures , 2ª Ed., John Wiley & Sons Inc., 1974, p 687-703, ISBN   978-0-471-49369-3 .
• BE Warren, X-Ray Diffraction , Addison-Wesley Publishing Co., 1969, p 251-254, ISBN   0-201-08524-0 .

Referências