Spline Centrípeta Catmull – Rom - Centripetal Catmull–Rom spline

Em computação gráfica , o spline Catmull-Rom centrípeto é uma forma variante do spline Catmull-Rom , originalmente formulado por Edwin Catmull e Raphael Rom , que pode ser avaliado usando um algoritmo recursivo proposto por Barry e Goldman. É um tipo de spline de interpolação (uma curva que passa por seus pontos de controle) definida por quatro pontos de controle , com a curva desenhada apenas de a . ${\ displaystyle \ mathbf {P} _ {0}, \ mathbf {P} _ {1}, \ mathbf {P} _ {2}, \ mathbf {P} _ {3}}$${\ displaystyle \ mathbf {P} _ {1}}$${\ displaystyle \ mathbf {P} _ {2}}$

Interpolação de spline Catmull-Rom com quatro pontos

Definição

Formulação piramidal de Barry e Goldman

Parametrização de nós para o algoritmo Catmull-Rom

Deixe denotar um ponto. Para um segmento de curva definido por pontos e sequência de nós , a spline Catmull-Rom centrípeta pode ser produzida por: ${\ displaystyle \ mathbf {P} _ {i} = [x_ {i} \ quad y_ {i}] ^ {T}}$${\ displaystyle \ mathbf {C}}$${\ displaystyle \ mathbf {P} _ {0}, \ mathbf {P} _ {1}, \ mathbf {P} _ {2}, \ mathbf {P} _ {3}}$${\ displaystyle t_ {0}, t_ {1}, t_ {2}, t_ {3}}$

${\ displaystyle \ mathbf {C} = {\ frac {t_ {2} -t} {t_ {2} -t_ {1}}} \ mathbf {B} _ {1} + {\ frac {t-t_ { 1}} {t_ {2} -t_ {1}}} \ mathbf {B} _ {2}}$

Onde

${\ displaystyle \ mathbf {B} _ {1} = {\ frac {t_ {2} -t} {t_ {2} -t_ {0}}} \ mathbf {A} _ {1} + {\ frac { t-t_ {0}} {t_ {2} -t_ {0}}} \ mathbf {A} _ {2}}$

${\ displaystyle \ mathbf {B} _ {2} = {\ frac {t_ {3} -t} {t_ {3} -t_ {1}}} \ mathbf {A} _ {2} + {\ frac { t-t_ {1}} {t_ {3} -t_ {1}}} \ mathbf {A} _ {3}}$

${\ displaystyle \ mathbf {A} _ {1} = {\ frac {t_ {1} -t} {t_ {1} -t_ {0}}} \ mathbf {P} _ {0} + {\ frac { t-t_ {0}} {t_ {1} -t_ {0}}} \ mathbf {P} _ {1}}$

${\ displaystyle \ mathbf {A} _ {2} = {\ frac {t_ {2} -t} {t_ {2} -t_ {1}}} \ mathbf {P} _ {1} + {\ frac { t-t_ {1}} {t_ {2} -t_ {1}}} \ mathbf {P} _ {2}}$

${\ displaystyle \ mathbf {A} _ {3} = {\ frac {t_ {3} -t} {t_ {3} -t_ {2}}} \ mathbf {P} _ {2} + {\ frac { t-t_ {2}} {t_ {3} -t_ {2}}} \ mathbf {P} _ {3}}$

e

${\ displaystyle t_ {i + 1} = \ left [{\ sqrt {(x_ {i + 1} -x_ {i}) ^ {2} + (y_ {i + 1} -y_ {i}) ^ { 2}}} \ right] ^ {\ alpha} + t_ {i}}$

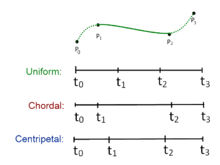
em que varia de 0 a 1 para parametrização de nós, e com . Para spline Catmull-Rom centrípeta, o valor de é . Quando , a curva resultante é o spline Catmull-Rom uniforme padrão ; quando , o produto é um spline Catmull-Rom cordal . ${\ displaystyle \ alpha}$${\ displaystyle i = 0,1,2,3}$${\ displaystyle t_ {0} = 0}$${\ displaystyle \ alpha}$${\ displaystyle 0,5}$${\ displaystyle \ alpha = 0}$${\ displaystyle \ alpha = 1}$

Animação Gif para parametrização uniforme , centrípeta e cordal de Catmull – Rom spline dependendo do valor α

Conectando -se às equações spline e mostra que o valor da curva spline em é . Da mesma forma, a substituição nas equações spline mostra que em . Isso é verdadeiro independentemente do valor de, pois a equação de não é necessária para calcular o valor de nos pontos e . ${\ displaystyle t = t_ {1}}$${\ displaystyle \ mathbf {A} _ {1}, \ mathbf {A} _ {2}, \ mathbf {A} _ {3}, \ mathbf {B} _ {1}, \ mathbf {B} _ { 2},}$${\ displaystyle \ mathbf {C}}$${\ displaystyle t_ {1}}$${\ displaystyle \ mathbf {C} = \ mathbf {P} _ {1}}$${\ displaystyle t = t_ {2}}$${\ displaystyle \ mathbf {C} = \ mathbf {P} _ {2}}$${\ displaystyle t_ {2}}$${\ displaystyle \ alpha}$${\ displaystyle t_ {i + 1}}$${\ displaystyle \ mathbf {C}}$${\ displaystyle t_ {1}}$${\ displaystyle t_ {2}}$

Segmento de spline Catmull-Rom centrípeto 3D .

A extensão para pontos 3D é simplesmente alcançada considerando um ponto 3D genérico e ${\ displaystyle \ mathbf {P} _ {i} = [x_ {i} \ quad y_ {i} \ quad z_ {i}] ^ {T}}$${\ displaystyle \ mathbf {P} _ {i}}$

${\ displaystyle t_ {i + 1} = \ left [{\ sqrt {(x_ {i + 1} -x_ {i}) ^ {2} + (y_ {i + 1} -y_ {i}) ^ { 2} + (z_ {i + 1} -z_ {i}) ^ {2}}} \ direita] ^ {\ alpha} + t_ {i}}$

Vantagens

A spline Centrípeta Catmull-Rom tem várias propriedades matemáticas desejáveis ​​em comparação com o original e os outros tipos de formulação Catmull-Rom. Primeiro, ele não formará um loop ou autointerseção dentro de um segmento de curva. Em segundo lugar, a cúspide nunca ocorrerá dentro de um segmento de curva. Terceiro, ele segue os pontos de controle com mais firmeza.

Nesta figura, há uma autointerseção / loop no spline Catmull-Rom uniforme (verde), enquanto para o spline Catmull-Rom cordal (vermelho), a curva não segue rigidamente através dos pontos de controle.

Outros usos

Na visão computacional , o spline Catmull-Rom centrípeto foi usado para formular um modelo ativo para segmentação. O método é denominado modelo spline ativo . O modelo é elaborado com base no modelo de forma ativa , mas usa spline Catmull-Rom centrípeta para unir dois pontos sucessivos (o modelo de forma ativa usa linha reta simples), de modo que o número total de pontos necessários para representar uma forma seja menor. O uso de spline Catmull-Rom centrípeto torna o treinamento de um modelo de forma muito mais simples e permite uma maneira melhor de editar um contorno após a segmentação.

Exemplo de código em Python

A seguir está uma implementação do spline Catmull-Rom em Python que produz o gráfico mostrado abaixo.

import numpy
import matplotlib.pyplot as plt

def CatmullRomSpline(P0, P1, P2, P3, nPoints=100):
    """
    P0, P1, P2, and P3 should be (x,y) point pairs that define the Catmull-Rom spline.
    nPoints is the number of points to include in this curve segment.
    """
    # Convert the points to numpy so that we can do array multiplication
    P0, P1, P2, P3 = map(numpy.array, [P0, P1, P2, P3])

    # Parametric constant: 0.5 for the centripetal spline, 0.0 for the uniform spline, 1.0 for the chordal spline.
    alpha = 0.5
    # Premultiplied power constant for the following tj() function.
    alpha = alpha/2
    def tj(ti, Pi, Pj):
        xi, yi = Pi
        xj, yj = Pj
        return ((xj-xi)**2 + (yj-yi)**2)**alpha + ti

    # Calculate t0 to t4
    t0 = 0
    t1 = tj(t0, P0, P1)
    t2 = tj(t1, P1, P2)
    t3 = tj(t2, P2, P3)

    # Only calculate points between P1 and P2
    t = numpy.linspace(t1, t2, nPoints)

    # Reshape so that we can multiply by the points P0 to P3
    # and get a point for each value of t.
    t = t.reshape(len(t), 1)
    print(t)
    A1 = (t1-t)/(t1-t0)*P0 + (t-t0)/(t1-t0)*P1
    A2 = (t2-t)/(t2-t1)*P1 + (t-t1)/(t2-t1)*P2
    A3 = (t3-t)/(t3-t2)*P2 + (t-t2)/(t3-t2)*P3
    print(A1)
    print(A2)
    print(A3)
    B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2
    B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3

    C = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2
    return C

def CatmullRomChain(P):
    """
    Calculate Catmull–Rom for a chain of points and return the combined curve.
    """
    sz = len(P)

    # The curve C will contain an array of (x, y) points.
    C = []
    for i in range(sz-3):
        c = CatmullRomSpline(P[i], P[i+1], P[i+2], P[i+3])
        C.extend(c)

    return C

# Define a set of points for curve to go through
Points = [[0, 1.5], [2, 2], [3, 1], [4, 0.5], [5, 1], [6, 2], [7, 3]]

# Calculate the Catmull-Rom splines through the points
c = CatmullRomChain(Points)

# Convert the Catmull-Rom curve points into x and y arrays and plot
x, y = zip(*c)
plt.plot(x, y)

# Plot the control points
px, py = zip(*Points)
plt.plot(px, py, 'or')

plt.show()

Gráfico obtido pelo código de exemplo Python dado acima

Exemplo de código em Unity C #

using UnityEngine;
using System.Collections;
using System.Collections.Generic;

public class Catmul : MonoBehaviour {

	// Use the transforms of GameObjects in 3d space as your points or define array with desired points
	public Transform[] points;
	
	// Store points on the Catmull curve so we can visualize them
	List<Vector2> newPoints = new List<Vector2>();
	
	// How many points you want on the curve
	uint numberOfPoints = 10;
	
	// Parametric constant: 0.0 for the uniform spline, 0.5 for the centripetal spline, 1.0 for the chordal spline
	public float alpha = 0.5f;
	
	/////////////////////////////
	
	void Update()
	{
	    CatmulRom();
	}
	
	void CatmulRom()
	{
		newPoints.Clear();

		Vector2 p0 = points[0].position; // Vector3 has an implicit conversion to Vector2
		Vector2 p1 = points[1].position;
		Vector2 p2 = points[2].position;
		Vector2 p3 = points[3].position;

		float t0 = 0.0f;
		float t1 = GetT(t0, p0, p1);
		float t2 = GetT(t1, p1, p2);
		float t3 = GetT(t2, p2, p3);

		for (float t=t1; t<t2; t+=((t2-t1)/(float)numberOfPoints))
		{
		    Vector2 A1 = (t1-t)/(t1-t0)*p0 + (t-t0)/(t1-t0)*p1;
		    Vector2 A2 = (t2-t)/(t2-t1)*p1 + (t-t1)/(t2-t1)*p2;
		    Vector2 A3 = (t3-t)/(t3-t2)*p2 + (t-t2)/(t3-t2)*p3;
		    
		    Vector2 B1 = (t2-t)/(t2-t0)*A1 + (t-t0)/(t2-t0)*A2;
		    Vector2 B2 = (t3-t)/(t3-t1)*A2 + (t-t1)/(t3-t1)*A3;
		    
		    Vector2 C = (t2-t)/(t2-t1)*B1 + (t-t1)/(t2-t1)*B2;
		    
		    newPoints.Add(C);
		}
	}

	float GetT(float t, Vector2 p0, Vector2 p1)
	{
	    float a = Mathf.Pow((p1.x-p0.x), 2.0f) + Mathf.Pow((p1.y-p0.y), 2.0f);
	    float b = Mathf.Pow(a, alpha * 0.5f);
	   
	    return (b + t);
	}
	
	// Visualize the points
	void OnDrawGizmos()
	{
	    Gizmos.color = Color.red;
	    foreach (Vector2 temp in newPoints)
	    {
	        Vector3 pos = new Vector3(temp.x, temp.y, 0);
	        Gizmos.DrawSphere(pos, 0.3f);
	    }
	}
}

Para uma implementação no espaço 3D, após converter os pontos Vector2 em Vector3, a primeira linha da função GetT deve ser alterada para esta: Mathf.Pow((p1.x-p0.x), 2.0f) + Mathf.Pow((p1.y-p0.y), 2.0f) + Mathf.Pow((p1.z-p0.z), 2.0f);

Exemplo de código em Unreal C ++

float GetT( float t, float alpha, const FVector& p0, const FVector& p1 )
{
    auto d  = p1 - p0;
    float a = d | d; // Dot product
    float b = FMath::Pow( a, alpha*.5f );
    return (b + t);
}

FVector CatmullRom( const FVector& p0, const FVector& p1, const FVector& p2, const FVector& p3, float t /* between 0 and 1 */, float alpha=.5f /* between 0 and 1 */ )
{
    float t0 = 0.0f;
    float t1 = GetT( t0, alpha, p0, p1 );
    float t2 = GetT( t1, alpha, p1, p2 );
    float t3 = GetT( t2, alpha, p2, p3 );
    t = FMath::Lerp( t1, t2, t );
    FVector A1 = ( t1-t )/( t1-t0 )*p0 + ( t-t0 )/( t1-t0 )*p1;
    FVector A2 = ( t2-t )/( t2-t1 )*p1 + ( t-t1 )/( t2-t1 )*p2;
    FVector A3 = ( t3-t )/( t3-t2 )*p2 + ( t-t2 )/( t3-t2 )*p3;
    FVector B1 = ( t2-t )/( t2-t0 )*A1 + ( t-t0 )/( t2-t0 )*A2;
    FVector B2 = ( t3-t )/( t3-t1 )*A2 + ( t-t1 )/( t3-t1 )*A3;
    FVector C  = ( t2-t )/( t2-t1 )*B1 + ( t-t1 )/( t2-t1 )*B2;
    return C;
}

Veja também

• Splines cúbicas hermite

Referências

links externos

• Curva Catmull-Rom sem cúspides e sem autointerseções  - implementação em Java
• Curva Catmull-Rom sem cúspides e sem autointerseções  - implementação simplificada em C ++
• Splines Catmull-Rom  - geração interativa via Python, em um notebook Jupyter